Wanderson Luiz de França Filho1, Roberto Chust Carvalho1, André Luís Christoforo1, Francisco Antonio Rocco Lahr2
1Department of Civil Engineering (DECiv), Federal University of São Carlos (UFSCar) - São Carlos, Brazil
2Department of Structural Engineering, São Paulo University (EESC/USP), São Carlos, Brazil
Correspondence to: André Luís Christoforo, Department of Civil Engineering (DECiv), Federal University of São Carlos (UFSCar) - São Carlos, Brazil.
| Email: |  |
Copyright © 2017 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
This research presents the development and implementation area of algorithms for geometric dimensioning rigid-foot-isolated reinforced concrete subjected to the under biaxial bending. The area algorithms are valid for square footing, homothetic to the pillar with equal Bludgers and a rectangular dimension unrelated to the pillar. In the development of algorithms, it is considered that the load is positioned within the central core footing inertia, i.e., applicable only in cases of small eccentricities. This issue is relevant when considering that normally the geometry of footing subjected to under biaxial bending with poor accuracy is calculated, resulting in inaccurate dimensions therefore may increase the cost of the element. In addition to the assumptions and analyzes used in the development algorithms, several numerical examples are shown to demonstrate their efficiency. Examples were prepared considering the concrete consumption for each geometric type of footing. Ultimately, a comparison is made between the results, setting the most economical type of geometry in terms of consumption of concrete.
Keywords:
Footing, Reinforced concrete, Under biaxial bending
Cite this paper: Wanderson Luiz de França Filho, Roberto Chust Carvalho, André Luís Christoforo, Francisco Antonio Rocco Lahr, Dimensioning of Isolated Footing Submitted to the under Biaxial Bending Considering the Low Concrete Consumption, International Journal of Materials Engineering , Vol. 7 No. 1, 2017, pp. 1-11. doi: 10.5923/j.ijme.20170701.01.
1. Introduction
Foundations are structural elements, usually in reinforced concrete, whose function is to ensure the stability of the work and transmit the loads acting on the structure resistant layer of soil. They can be classified as superficial or deep [1].The choice of the type of foundation to use for a particular building should only be made after consideration of some elements, such as the study of adjacent buildings as well as their type of foundation and state of the same, the characteristics and the mechanical properties of the soil on-site, the groundwater level, the values of the loads to be transmitted to the foundation, type of material that makes up the superstructure, the cost, some technical aspects for carrying out the work, the types of foundation on the market and others factors [1]. Direct foundation is the first type of foundation to be searched and just presenting advantage when the area occupied by the Foundation cover between 50% to 70% of the available area. However, this type of foundation should not be used in cases of non-compacted embankment, soft clay, soft sand and very soft, collapsible soils, there is water where the lowering of the water table is not justified [1]. The footing is a type of shallow foundation and can be of the type associated, individually or race. It is intended to receive all active actions in the structure (pillars, walls or walls) and distribute them directly into the ground so as not to cause differential settlements, which may adversely affect the structural system, and not to break the ground. Its main advantage is that they are fast running (which is not the case of caissons) and do not require the use of specific equipment and transport (such as cuttings). This type of foundation is recommended especially when the ground is homogeneous [2].As a structural element, the footing works by transmitting all actions of the superstructure through the stress distribution under the foundation base to the ground. Therefore, the elements of the structure of footing should provide adequate resistance requests and should be properly sized. The geometric shape will depend on the design data, essentially the load capacity of the soil and the load to be transmitted [2].Among isolated footings, one can present various geometries and, in some cases, they can be related to the dimensions of the pillar.For most cases, it adopts the following types of geometries in plant:Ÿ Circular:Ÿ Square (Fig. 11);Ÿ Rectangular:§ With equal overhangs (Figure 9);§ Homothetic to the pillar (Figure 8);§ Unrelated to the pillar (Figure 7).For elevation, [3] and [4] mention that the footing can have a constant section (straight) or variable height (pyramidal), as shown in Figure 1a and 1b, respectively.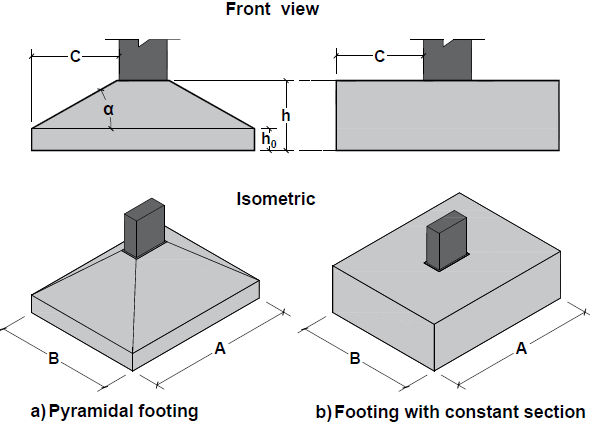 | Figure 1. Types of isolated footing |
[5] mention that, by their geometric characteristics, pyramidal footings can make a great transmission of load acting on the columns to the ground. Nevertheless, this solution is more expensive, especially regarding the use of forms, and requires concrete with dry consistency, making its density tends to be deficient. [2] suggests that the inclination α must be around 30 - which corresponds to the angle of internal friction of the concrete average compactness, because there is no slip of the concrete, allowing the use of side forms height h0 (Figure 1a). This solution is cost-effective, whereas the pyramidal shape of the footing generates considerable savings in the consumption of concrete. Therefore, this research evaluate the pyramidal footing structural model.
2. Stress Distribution in the Soil
[3] reported that the stress distribution in the soil can be affected by factors such as the stiffness -related foundation, soil properties, the intensity and characteristics of applied loads, and especially the area of the footing base.The form of the stress distribution in the soil caused by a footing subjected to a centered axial load is directly dependent on several factors such as: footing classification as stiffness, soil type (clay or sandy), load capacity of the soil and intensity of applied load.Both rigid (Figure 2) or flexible footing (Figure 3), the real stress distribution is not uniform and the bending moment varies along the proper footing geometry, but it is recommended for structural calculation purposes, the pressures at the base of the foundation can be admitted as evenly distributed, except for supported foundations on rock.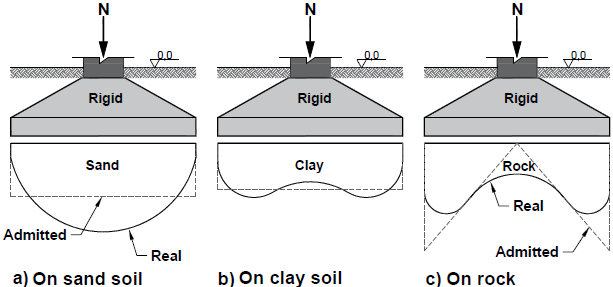 | Figure 2. Distribution of pressure on rigid or stiffness footing |
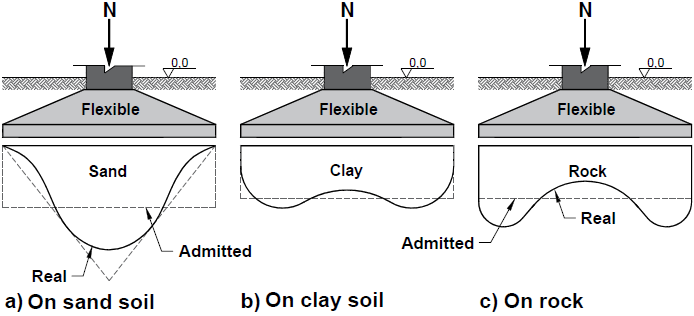 | Figure 3. Distribution of pressure on flexible footing |
3. Used Criteria
This research used the rigid footing, thus the height (h) of the footing, shown in Figure 4, is conditioned with the factor of rigidity. For this, we used the following criteria stiffness: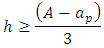 Where: Ÿ h= height of the footing;Ÿ A= dimension of the footing in one direction;Ÿ ap= is the dimension of the Pillar in the same direction.When checking the expression above, in both directions, the footing is considered rigid. Otherwise, the footing is considered flexible.
Where: Ÿ h= height of the footing;Ÿ A= dimension of the footing in one direction;Ÿ ap= is the dimension of the Pillar in the same direction.When checking the expression above, in both directions, the footing is considered rigid. Otherwise, the footing is considered flexible.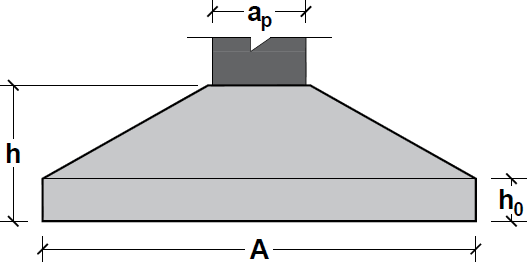 | Figure 4. Isolated pyramidal footing |
To determine the height 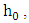 shown in Figure 4, [4] recommends the following criteria:
shown in Figure 4, [4] recommends the following criteria: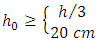 To calculate the volume, uses the truncated pyramid expression (V), expressed by Equation 1.
To calculate the volume, uses the truncated pyramid expression (V), expressed by Equation 1.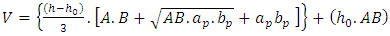 | (1) |
4. Development of Algorithms
The algorithms are designed so that the entire base of the footing becomes compressed, or in cases of small eccentricities. In such cases, the eccentricity is such that the load is positioned within the central core of inertia of the footing, then the neutral axis passes out of the element. For this, must satisfy the two conditions: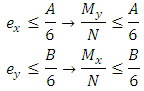 In the case of large eccentricities that is, where the neutral axis passes through the footing, this solution is not valid since for the analysis of the stresses is necessary to use other theories, as shown in the researchers developed by [6-9].Figure 5 shows an area subjected to any under biaxial bending, where stress are different in the four corners of the contact surface. In this case, in which the neutral axis passes out of the element, consider the hypotheses of the general theory of bending, that is, the stress distribution vary linearly. So:
In the case of large eccentricities that is, where the neutral axis passes through the footing, this solution is not valid since for the analysis of the stresses is necessary to use other theories, as shown in the researchers developed by [6-9].Figure 5 shows an area subjected to any under biaxial bending, where stress are different in the four corners of the contact surface. In this case, in which the neutral axis passes out of the element, consider the hypotheses of the general theory of bending, that is, the stress distribution vary linearly. So: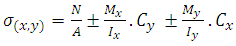 | (2) |
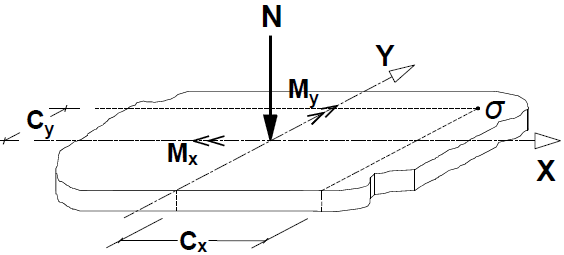 | Figure 5. Area submitted to the composed oblique bending. Adapted from [10] |
From Equation 2, the meaning of the variables are:Ÿ A= Contact Área;Ÿ N = Axial Load;Ÿ 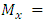 Moment in direction of axis X;Ÿ
Moment in direction of axis X;Ÿ 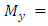 Moment in the direction of axis Y;Ÿ
Moment in the direction of axis Y;Ÿ 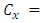 Distance in direction X from the axis Y;Ÿ
Distance in direction X from the axis Y;Ÿ 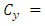 Distance in direction Y from the axis X;Ÿ
Distance in direction Y from the axis X;Ÿ 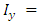 Moment of inertia around the axis Y;Ÿ
Moment of inertia around the axis Y;Ÿ 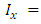 Moment of inertia around the axis X.Figure 6 shows a rectangular area subjected to the under biaxial, where stress are different in the four corners of the contact surface.
Moment of inertia around the axis X.Figure 6 shows a rectangular area subjected to the under biaxial, where stress are different in the four corners of the contact surface.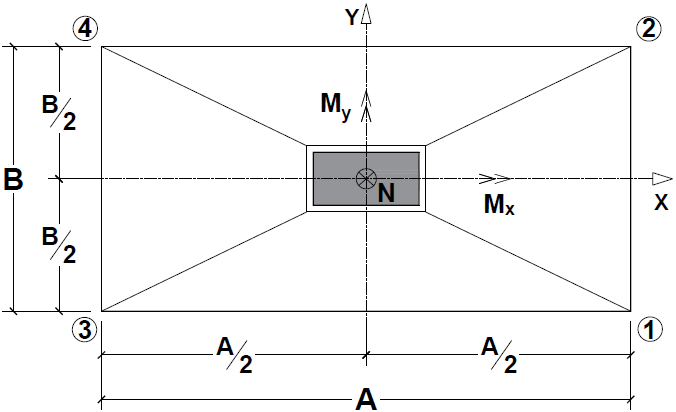 | Figure 6. Rectangular area submitted to under biaxial bending |
Where: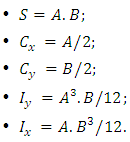 Substituting in Equation 2:
Substituting in Equation 2: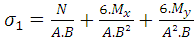 | (3) |
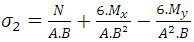 | (4) |
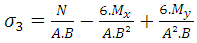 | (5) |
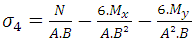 | (6) |
4.1. Footing with Unrelated Dimensions to the Column
The mathematical model for this geometry (Figure 7) was developed by [10]. This type of footing has Ca ≠ Cb but unlike homothetic footing, and have no relation with the column (the dimensions are arbitrary plants).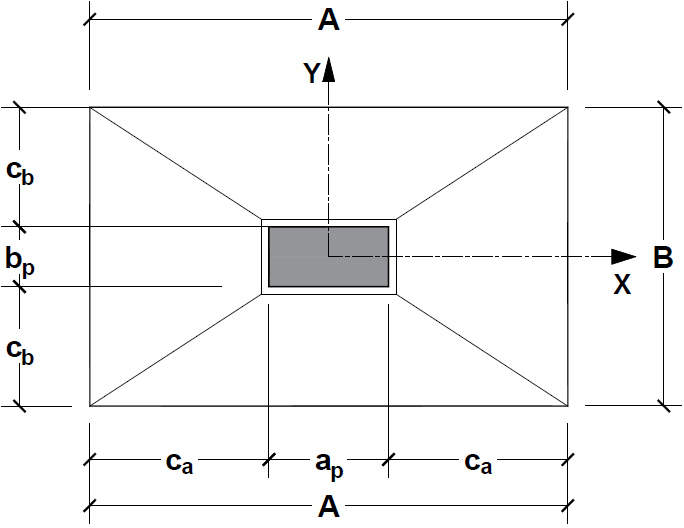 | Figure 7. Footing with any relation in plant |
Where:Ÿ Ca and Cb are the overhangs of the footing;Ÿ A is the biggest dimension of the footing;Ÿ B is the smallest dimension of the footing;Ÿ ap is the biggest dimension of the column;Ÿ bp is the smallest dimension of the column.For this, considering the following limits for the eccentricities: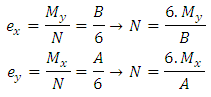 Equating, we have:
Equating, we have: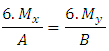 Then:
Then: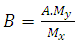 | (7) |
1th condition – The minimun stress is zero, so: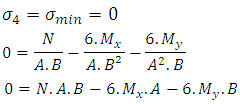 | (8) |
Substituting (7) in (8):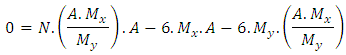 Simplifying:
Simplifying: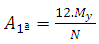 | (9) |
Analogously: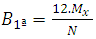 | (10) |
2th condition - The maximum stress is equal to the permissible tension of the soil, then: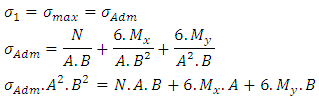 Simplifying:
Simplifying: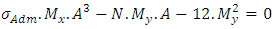 | (11) |
Solving Equation 11 gives the value A. Then, the value of B is given by: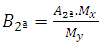 | (12) |
Solving Equations 11 and 12 find out the values A and B, respectively, of a rectangular footing, when the maximum stresses is equal to the load capacity of the soil. Therefore, the final dimensions of the footing are found, as follows: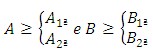
4.2. Homothetics Footing to the Column
The homothetic footing, shown in Figure 8, are those in which the relation between the sides of the base is the same between the sides of the pillar section, that is: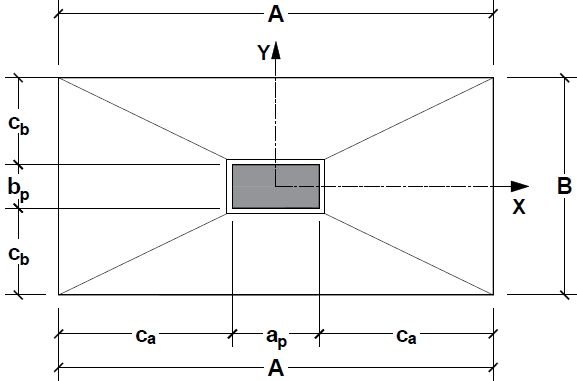 | Figure 8. Homothetics Footing to the pillar |
Where:Ÿ Ca e Cb is the overhangs of the footing.Ÿ A is the biggest dimension of the footing;Ÿ B is the smallest dimension of the footing;Ÿ ap is the biggest dimension of the column;Ÿ bp is the smallest dimension to the column.The relation (r) that determines the sides of the footing is: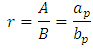 Then:
Then: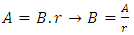 | (13) |
1th condition - The minimum stress is zero, then: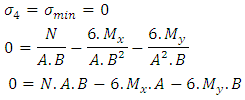 | (14) |
Replacing (13) in (14), is obtained: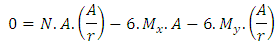 Simplifying:
Simplifying: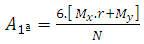 | (15) |
From Equation 15, obtains the values of A. Then: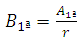 | (16) |
Solving Equations 15 and 16 we found the values of A and B, respectively, of a homothetic footing when the minimum stress is zero.2th condition - The maximum stress is equal to the permissible tension of the soil, then: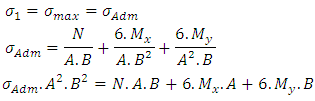 | (17) |
Replacing (13) in (17), we obtain: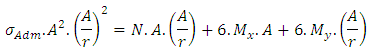 Simplifying:
Simplifying: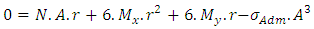 | (18) |
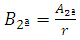 | (19) |
Solving Equations 18 and 19 finds the values A and B, respectively, of a homothetic footing, when the maximum stress is equal to the load capacity of the soil. Therefore, the final dimensions of the footing are found as following: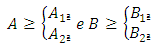
4.3. Footing with Equal Overhangs
The footing with equal overhangs, shown in Figure 9, is one of the most used types geometric because the armature is approximately equal in both directions.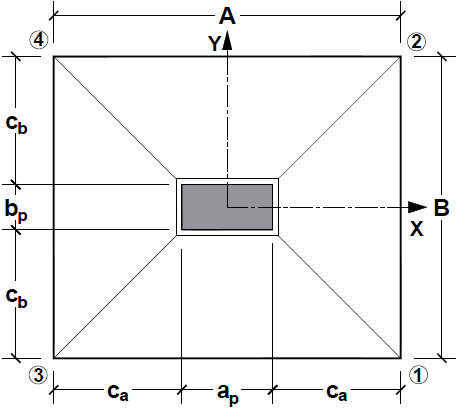 | Figure 9. Footing with equal overhangs |
Where:Ÿ Ca e Cb are the overhangs of the footing;Ÿ A is the biggest dimension of the footing;Ÿ B is the smallest dimension of the footing;Ÿ ap is the biggest dimension of the column;Ÿ bp is the smallest dimension of the column.In this case Ca = Cb, then: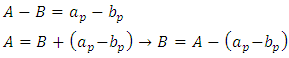 Denominating:
Denominating: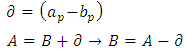 | (20) |
1th condition - The minimum voltage is zero, then: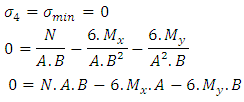 | (21) |
Substituting (20) in (21), we have: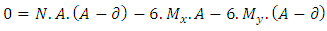 Simplifying:
Simplifying: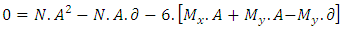 | (22) |
Extracting the root of the Equation 22 gives the value A. Then, from Equation 20, one obtains the value of B. Hence: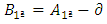 | (23) |
Solving Equations 22 and 23 are the values of A and B, respectively, of a footing with the same balance, when the minimum voltage is zero.2th condition - The maximum voltage is equal to the load capacity of the soil, then: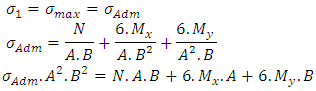 | (24) |
Substituting (20) in (24), obtains: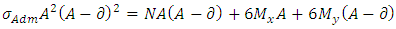 | (25) |
Simplifying: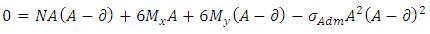 Extracting the root of Equation 25, we obtains the value A. Then, from Equation 20, we obtains the value of B. Hence:
Extracting the root of Equation 25, we obtains the value A. Then, from Equation 20, we obtains the value of B. Hence: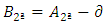 | (26) |
Solving Equations 25 and 26 results in the values of A and B, respectively, of a footing with the same balance, when the minimum stress is zero.Therefore, the final dimensions of the footing are found as follows: 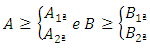
4.4. Square Footing
The mathematical model for this type of geometry was also developed by [10]. Figure 10 shows a square area of L sides submitted under biaxial bending, where tensions are different in the four corners of the contact surface.Where: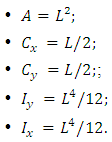 Therefore, the stress stays:
Therefore, the stress stays: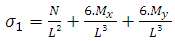 | (27) |
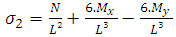 | (28) |
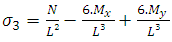 | (29) |
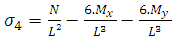 | (30) |
For the above conditions, the maximum eccentricities should be: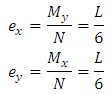
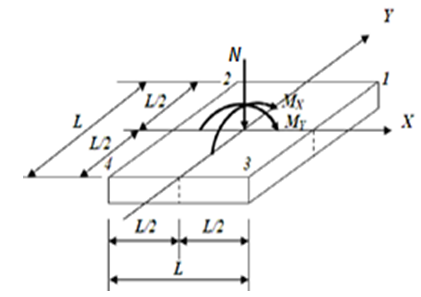 | Figure 10. Square area submitted under biaxial bending. Adapted from [10] |
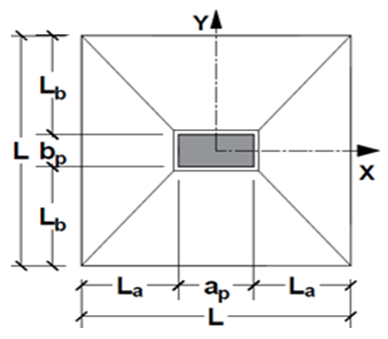 | Figure 11. Squares footing |
Where:Ÿ La= Lb= footing overhangs;Ÿ L is the side of the footingŸ ap is the biggest dimension of the column;Ÿ bp is the smallest dimension of the column.1th condition - The minimum stress is zero, then: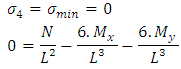 Simplifying:
Simplifying: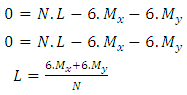 | (31) |
Solving Equation 31 we find L value of a square footing when the minimum stress is zero.2th condition - The maximum stress is equal to the load capacity of the soil, then: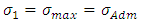
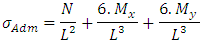 Simplifying:
Simplifying: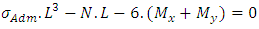 | (32) |
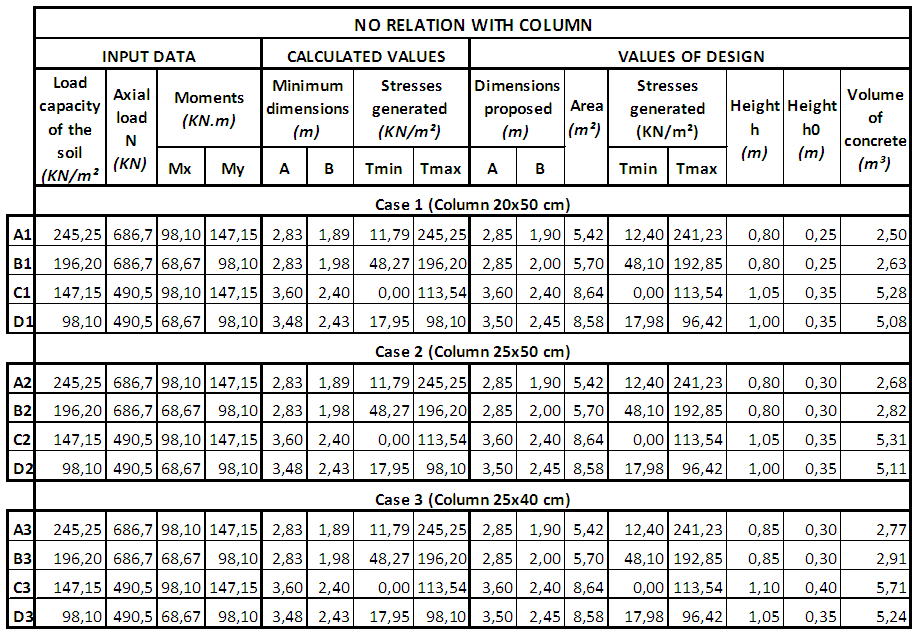
Extracting the root of Equation 32, L value of a square footing is obtained when the maximum stress is equal to the load capacity of the soil.The final value of the L side shall be the greater of the values obtained in the 1st and 2nd condition. So: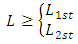
5. Application of Algorithms
The algorithms developed in the previous section determines the minimum area required for the entire base of the footing becomes compressed, thus brings the possibility to obtain a more economical geometric dimensioning. [10] shows that for the same requests, footings with circular section have advantage in terms of contact area over the footings of a square or rectangular section. However, the work presented by [10] presents a comparison, only in terms of contact area, excluding the specific consumption of different types of geometry.Therefore, we present a comparative study for cases of rectangular (no relation to the column, homothetic and equal Bludgers) and square footings.The study was done considering three cases of geometric dimensioning for the four different geometries footings and the results are shown in Table 1 (with equal balance), Table 2 (homothetic), Table 3 (without relation to the abutment) and Table 4 (square). The comparison was done by analyzing not only the area in plan, as shown in Table 5, but also the consumption of concrete. It uses the same at the end of requests and the results are compared, as shown in Figures 12 and 13.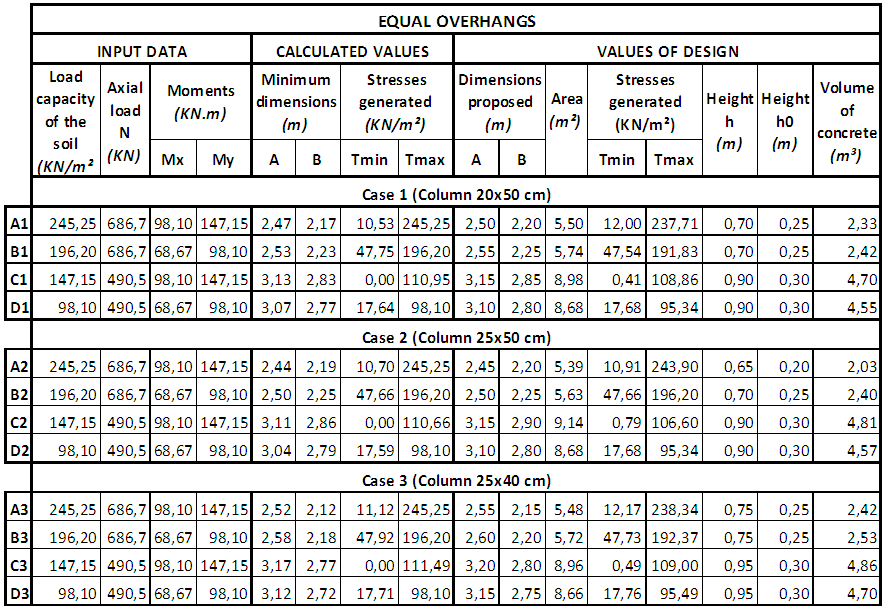 | Table 1. Results for footing with overhangs |
 | Table 2. Results for homothetic footing |
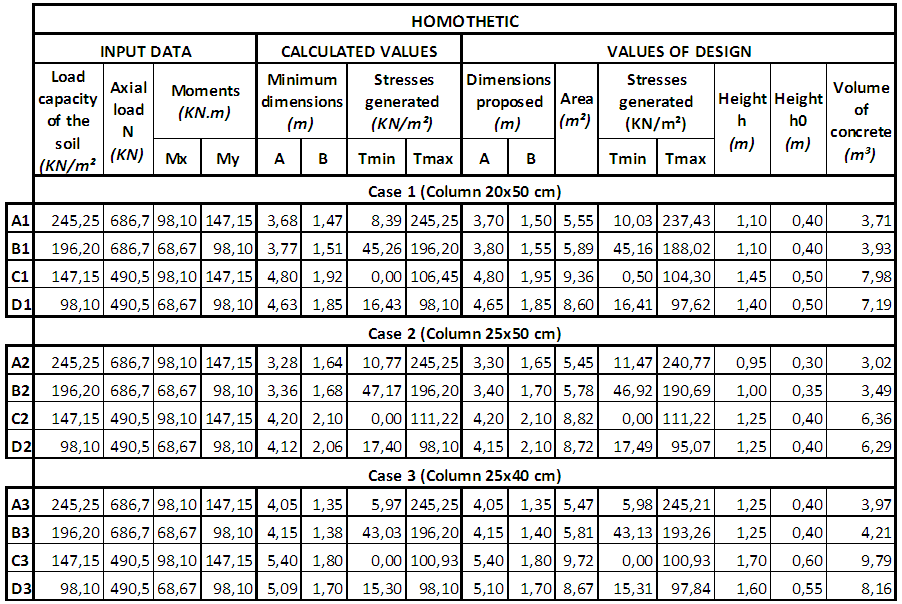
 | Table 3. Results to footing unrelated to the pillar |
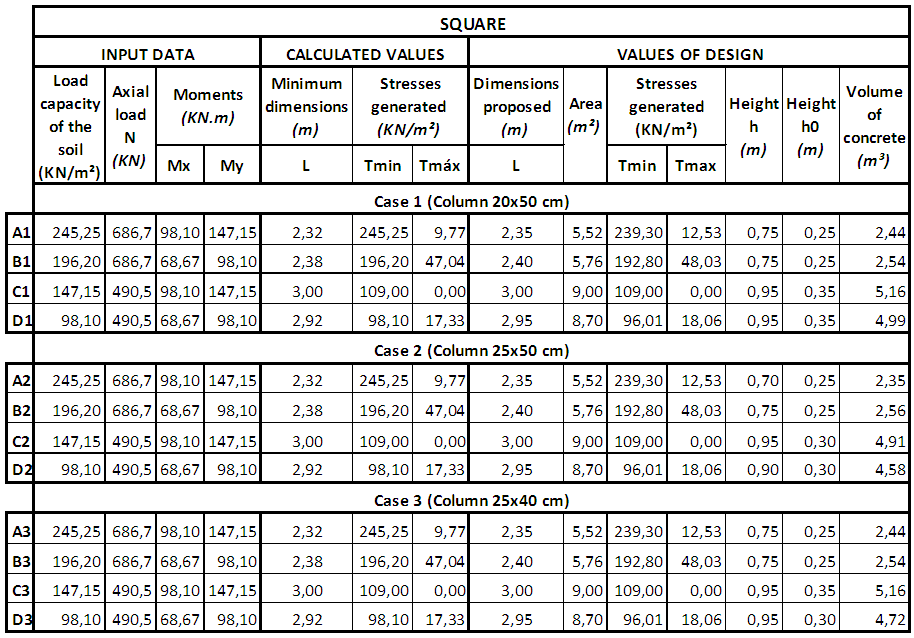 | Table 4. Results for square footing |
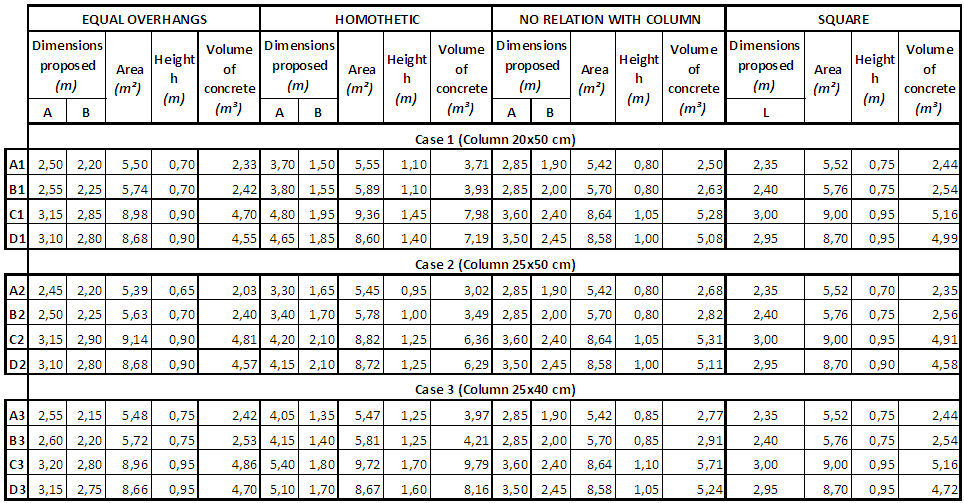 | Table 5. Comparison between all types |
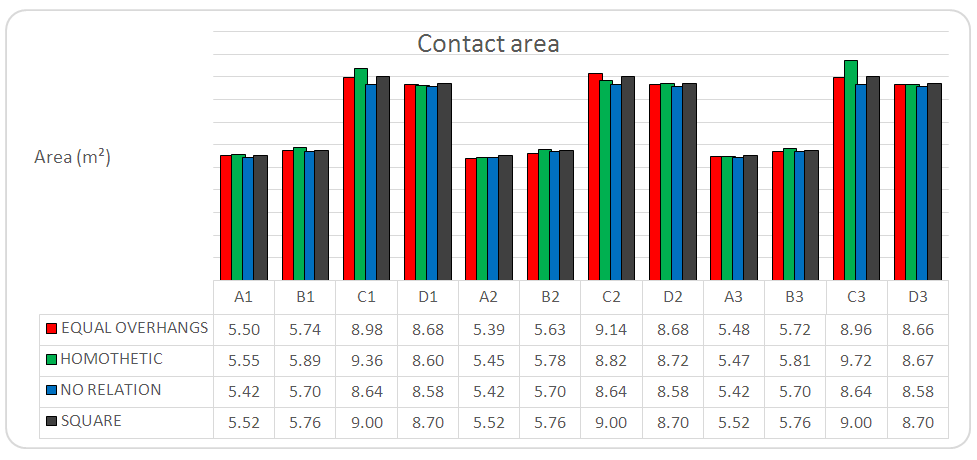 | Figure 12. Comparison between the required geometrics areas |
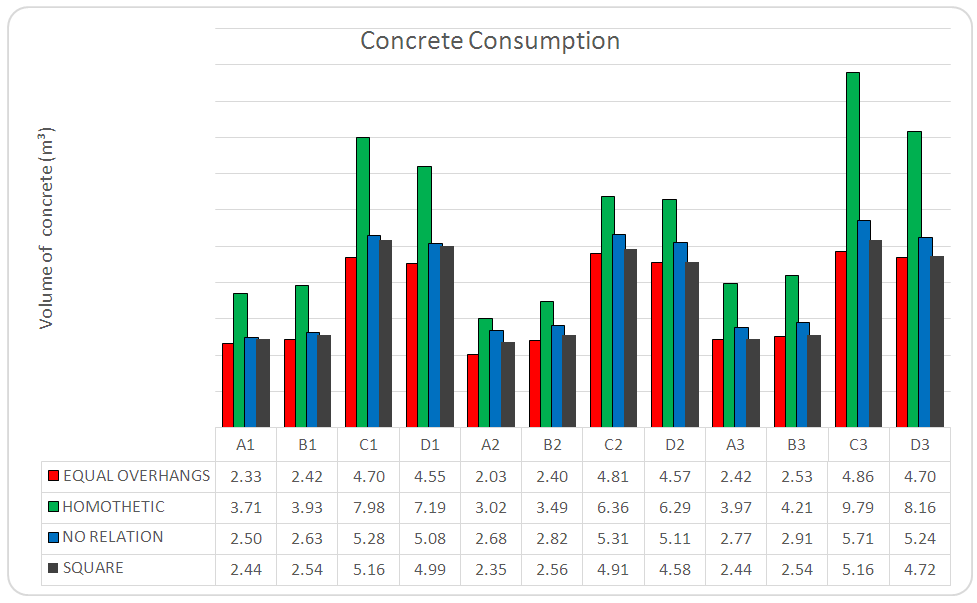 | Figure 13. Comparison between the concrete consumption |
6. Conclusions
Analyzing Figure 12, it is observed that there is a slight variation between the results which can be neglected due to the adoption of design values (multiples of 5 cm). Thus, it is clear that the area in the plant is not the determining factor in establishing the type of geometry that has more advantage in terms of actual consumption, unless they are footings with constant section, shown in Figure 1b.However, Figure 13 shows a greater variation in the results, and may conclude that, for the examples analyzed, footings with equal balances have advantage over others. Therefore, in terms of concrete economy, one can classify the geometries of pyramidal footings in the following sequence:Ÿ 1º - Rectangular with overhangs;Ÿ 2º - Square;Ÿ 3º - Rectangular unrelated to the pillar;Ÿ 4º - Rectangular homothetic to the pillar.The difference in concrete consumption is associated with rigidity of the geometry adopted. That is, even with the same area of the footing base with homothetic relationship requires a greater height to achieve the same rigidity value of the other.Regarding the requests, the models presented in this section can be used for the design of footing subjected to centric load with time in one direction or subjected to moment in both directions from the neutral axis passes out of the element.It is recommended that this model is used in soil where it can be considered a linear variation of tension being restricted to uses where the neutral line passing through the element.
ACKNOWLEDGMENTS
We are grateful to the Post Graduate Program in Structures and Civil Construction (PPGECiv) of the Federal University of São Carlos (UFSCar) and the University of São Paulo (USP) for the support.
References
| [1] | Alonso, U. R. Exercícios de Fundações. São Paulo: Edgard Blücher, 1983. 202 p. |
| [2] | Carvalho, R. C.; Pinheiro, L. M. Cálculo e Detalhamento de Estruturas Usuais de Concreto Armado. Volume 2, 2ª ed. São Paulo: PINI, 2013. 617 p. |
| [3] | Velloso, D. A.; Lopes, F. R. Fundações. Volume 1. Rio de Janeiro: Ed. Oficina de Textos, 2004. 226 p. |
| [4] | Silva, E. L. Análise dos Modelos Estruturais para Determinação dos Esforços Resistentes em Sapatas Isoladas. 1998. 122 p. Dissertação de Mestrado – EESC/USP – Escola de Engenharia de São Carlos, São Carlos, SP. 1998. |
| [5] | Moya, F. B. V.; Juárez, J. A. L.; Blázquez, L. B. Apuntes de Hormigón Armado. Adaptados a la Instrucción EHE-08. Escuela Politécnica Superior - Universidad de Alicante. San Vicente del Raspeig, España, 2012. |
| [6] | Özmen, G. Determination of Base Stresses in Rectangular Footing under Biaxial Bending. NDT&E International, Teknik Dergi Vol. 22, No. 4, October 2011. |
| [7] | Highther, W. H.; Anders, J. C. Dimensioning footing subjected to eccentric loads. ASCE - Journal of Geotechnical Engineering, Vol. 111, No. 5, pp. 659-665, 1985. |
| [8] | Gutiérrez, J. A. R.; Ochoa, J. D. A. Rigid Spread Footing Resting on Soil Subjected to Axial Load and Biaxial Bending. I: Simplified Analytical Method. ASCE - Journal of Geotechnical Engineering, Vol. 13, No. 2, pp. 109-119, 2013. |
| [9] | Bellos, J.; Bakas, N. P. High computational efficiency through generic analytical formulation for linear soil pressure distribution of rigid spread rectangular footing. ECCOMAS Congress 2016 - VII European Congress on Computational Methods in Applied Sciences and Engineering, Crete Island, Greece. June 2016. |
| [10] | Rojas, A. L. A comparative study for dimensioning of footing with respect to the contact surface on soil. International Journal of Innovative Computing, Information and Control, vol.10, no.4, pp.1313-1326, 2014. |






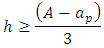 Where: Ÿ h= height of the footing;Ÿ A= dimension of the footing in one direction;Ÿ ap= is the dimension of the Pillar in the same direction.When checking the expression above, in both directions, the footing is considered rigid. Otherwise, the footing is considered flexible.
Where: Ÿ h= height of the footing;Ÿ A= dimension of the footing in one direction;Ÿ ap= is the dimension of the Pillar in the same direction.When checking the expression above, in both directions, the footing is considered rigid. Otherwise, the footing is considered flexible.
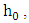 shown in Figure 4, [4] recommends the following criteria:
shown in Figure 4, [4] recommends the following criteria: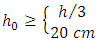 To calculate the volume, uses the truncated pyramid expression (V), expressed by Equation 1.
To calculate the volume, uses the truncated pyramid expression (V), expressed by Equation 1.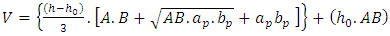
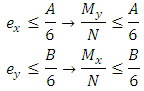 In the case of large eccentricities that is, where the neutral axis passes through the footing, this solution is not valid since for the analysis of the stresses is necessary to use other theories, as shown in the researchers developed by [6-9].Figure 5 shows an area subjected to any under biaxial bending, where stress are different in the four corners of the contact surface. In this case, in which the neutral axis passes out of the element, consider the hypotheses of the general theory of bending, that is, the stress distribution vary linearly. So:
In the case of large eccentricities that is, where the neutral axis passes through the footing, this solution is not valid since for the analysis of the stresses is necessary to use other theories, as shown in the researchers developed by [6-9].Figure 5 shows an area subjected to any under biaxial bending, where stress are different in the four corners of the contact surface. In this case, in which the neutral axis passes out of the element, consider the hypotheses of the general theory of bending, that is, the stress distribution vary linearly. So: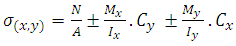

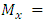 Moment in direction of axis X;Ÿ
Moment in direction of axis X;Ÿ 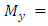 Moment in the direction of axis Y;Ÿ
Moment in the direction of axis Y;Ÿ 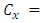 Distance in direction X from the axis Y;Ÿ
Distance in direction X from the axis Y;Ÿ 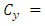 Distance in direction Y from the axis X;Ÿ
Distance in direction Y from the axis X;Ÿ 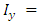 Moment of inertia around the axis Y;Ÿ
Moment of inertia around the axis Y;Ÿ 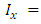 Moment of inertia around the axis X.Figure 6 shows a rectangular area subjected to the under biaxial, where stress are different in the four corners of the contact surface.
Moment of inertia around the axis X.Figure 6 shows a rectangular area subjected to the under biaxial, where stress are different in the four corners of the contact surface.
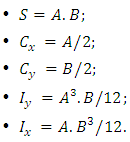 Substituting in Equation 2:
Substituting in Equation 2: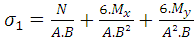
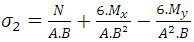
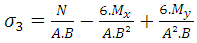
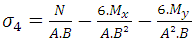

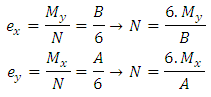 Equating, we have:
Equating, we have: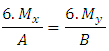 Then:
Then: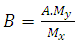
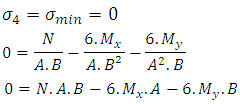
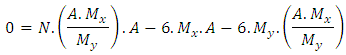 Simplifying:
Simplifying: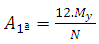
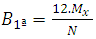
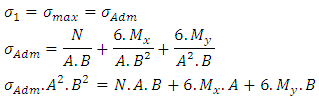 Simplifying:
Simplifying: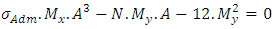
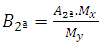
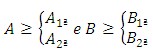

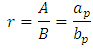 Then:
Then: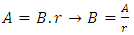
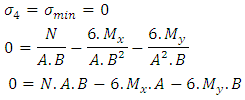
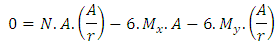 Simplifying:
Simplifying: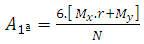
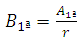
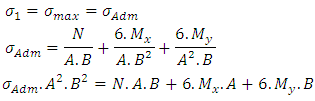
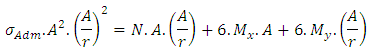 Simplifying:
Simplifying: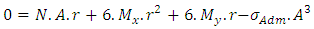
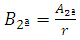
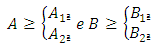

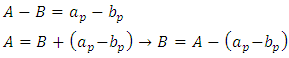 Denominating:
Denominating: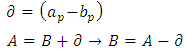
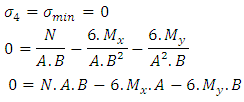
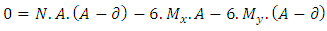 Simplifying:
Simplifying: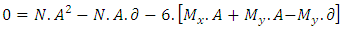
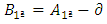
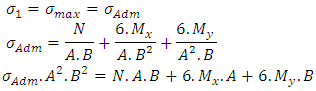
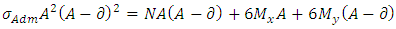
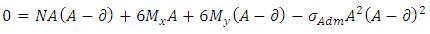 Extracting the root of Equation 25, we obtains the value A. Then, from Equation 20, we obtains the value of B. Hence:
Extracting the root of Equation 25, we obtains the value A. Then, from Equation 20, we obtains the value of B. Hence: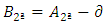
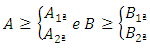
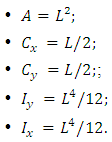 Therefore, the stress stays:
Therefore, the stress stays: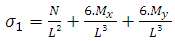
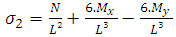
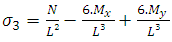
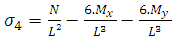
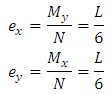


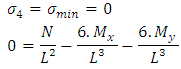 Simplifying:
Simplifying: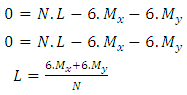
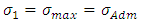
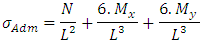 Simplifying:
Simplifying: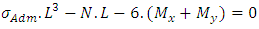







 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML