Tiago Hendrigo de Almeida1, Diego Henrique Almeida2, Leonardo Araújo Marcolin3, Decio Gonçalves3, André Luis Christoforo4, Francisco Antonio Rocco Lahr3
1Department of Material Engineering, Engineering School of São Carlos (SMM), São Carlos, Brazil
2Wood and Timber Structures Laboratory (LaMEM), São Paulo University (EESC/USP), São Carlos, Brazil
3Department of Structural Engineering (SET), São Paulo University (EESC/USP), São Carlos, Brazil
4Centre for Innovation and Technology in Composites – CITeC, Department of Civil Engineering (DECiv), Federal University of São Carlos, São Carlos, Brazil
Correspondence to: André Luis Christoforo, Centre for Innovation and Technology in Composites – CITeC, Department of Civil Engineering (DECiv), Federal University of São Carlos, São Carlos, Brazil.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
Abstract
Wood is a material of natural origin, whose properties are strongly influenced by their anatomical characteristics. In order to define a better interaction of the properties, studies aim to relate them in empirical equations past researches propose an experimental equation involving the density of the material and the coefficient of volumetric shrinkage, admitting the existence of a linear dependence between the variables in question. This work aims to evaluate the correlation between dry density and volumetric shrinkage coefficient in three Tropical Wood species: Cedrella sp., Cassia ferruginea and Vataireopsis araroba, separately evaluated and the three species together. Results shows that linear correlation between oven dry density and volumetric shrinkage coefficient in the three species together, but a different ratio than found in literature. To generalize the findings obtained here, further studies with larger number of species are required.
Keywords:
Dry density, Shrinkage, Wood properties
Cite this paper: Tiago Hendrigo de Almeida, Diego Henrique Almeida, Leonardo Araújo Marcolin, Decio Gonçalves, André Luis Christoforo, Francisco Antonio Rocco Lahr, Correlation between Dry Density and Volumetric Shrinkage Coefficient of Three Brazilian Tropical Wood Species, International Journal of Materials Engineering , Vol. 5 No. 1, 2015, pp. 1-4. doi: 10.5923/j.ijme.20150501.01.
1. Introduction
The moisture content of the wood influenced the average values of mechanical and physical properties [1, 2]. Wood with higher moisture content has higher moisture density and lower values of strength and stiffness [3, 4].The water of the wood can be classified by 3 forms [5-7]: Free Water – Above to fiber saturation point (FSP) and the water is more easily excreted in the drying; Higroscopic Water – below to FSP to 0% of moisture content, is among the cellulose molecules, and their removal occurs shrinkage of the wood; Constitution Water - from the elimination of hydroxyl groups of cellulose molecules and their elimination occur degradation of the wood.Moreover, the wood has hygroscopic property, that is, can gain or lose moisture according to its use. Therefore the importance of the equilibrium moisture content, which is the moisture content of the wood tends to reach when left in conditions of relative humidity and constant temperatures [8].These properties combined with the fact that the wood has lots of water, hamper one of the main activities of the processing of wood, that is drying, especially for the sector that uses solid wood as raw material [8, 9].Some drying defects as cracks and warping can be caused by wood shrinkage differences to dry, either by bad developed drying programs (which do not take into account the specie, direction to the fibers, moisture content and other characteristics) or because the anisotropic material property [5 - 8].The anisotropy is wood shrinkage difference in the radial, tangential and longitudinal directions relative to the grains which occurs in accordance with the increase or decrease in moisture content below the fiber saturation point [1, 10-11].At 2005, Pliura et al [12] studied the influence of density in the shrinkage at the three different main direction of the fiber of 384 different poplar hybrid clones grown at two different sites. They concluded that between the density and both radial and tangential shrinkage, for both sites, there were a significant positive correlation. Which means that, as the density increased, the longitudinal and tangential shrinkage did increase too. For the value of longitudinal shrinkage and the density, they obtained a negative correlation value.Korkut and Guller [13] found a statistically significant result for wood density and shrinkage, also for poplar and their hybrids. They evaluated the volume, tangential, and radial shrinkage with a positive correlation value. But for the longitudinal shrinkage, they obtained a weak correlation with density.In addition to these properties, Sotannde et al [14] studied the relationship of the grain direction of the fiber on the shrinkage in the Azadirachta indica wood. They obtained negative and highly significant (p < 0.01) for the relationship between density and anisotropic shrinkage. The highest influence was found on the radial plane, and the least was the tangential. Regarding the influence of the grain direction and the anisotropic shrinkage, the value obtained for them also shows a positive and highly significant relationship (p<0.01). They conclude that it may be possible to use density and grain orientation biometry to predict anisotropic shrinkage of the wood.One of the studies found was done with three Brazilian species of Eucalyptus with 5 different clones each. Batista, Klitzke and Taborda [15] evaluated the influence of density on the anisotropic shrinkage of the wood. They concluded that those properties had a relationship between the species, based on correlation values.Muñoz and Anta [16] had a sample of forty young trees of maritime pine for studying the density and shrinkage influence in clear and small wood specimens. The authors developed a general model for the prediction of volumetric shrinkage, utilizing oven dry density and ring width as predictor variables. The values for the correlations obtained were higher for volumetric and longitudinal shrinkage when analyzed with the density.Following the same line of research, Kiaei [17] investigated the correlation of a softwood, Pinus eldarica Medw, and determined a linear equation for oven dry density and volume shrinkage. The author obtained a significantly positive correlation with these two variables.The Brazilian and European Codes recommend the estimate of the properties of wood from a better known another [18, 19]. Other researches present relations between the different properties of wood, including those which take into account the density of the wood [20, 21].Kollmann and Coté [6] in their studies about physical properties of wood, developed the relationship between the dry density and volumetric shrinkage coefficient of typical Wood species from northern hemisphere, proposing linear correlation between these two properties.The aim of this research is to study the linear correlation between the dry density and the volumetric shrinkage coefficient of three Brazilian tropical wood species.
2. Material and Methods
The tests were realizes in the Wood and Timber Structures Laboratory (LaMEM), São Paulo University (EESC/USP).The physical properties studied in this research (dry density and volumetric shrinkage coefficient) were determined with experimental procedures according Brazilian Standard ABNT NBR 7190 [18].Were used three Tropical Brazilian Wood species from Legal Environmental Reserve in northern region of the Brazil: Cedrella sp., Cassia ferruginea e Vataireopsis araroba. For research were made 12 specimens for each species (Figure 1). | Figure 1. Wood specimen used in this research |
After determination of fiber saturation points (FSP) of the three Wood species, drying was carried out at the specimens in a kiln. | Figure 2. Kiln used of drying of the specimen |
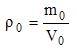 | (1) |
Where:ρ0 = dry density (g/cm³);m0 = mass of the specimen to 0% of moisture content (g);V0 = volume of the specimen to 0% of moisture content (cm³).The volumetric shrinkage of the Wood species studied in this research and volumetric shrinkage coefficients were determined for Equations 1 and 2, respectively.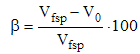 | (2) |
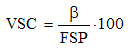 | (3) |
Where:β = volumetric shrinkage (%);Vpsf = mass of the specimen with fiber saturation point (g);VSC = volumetric shrinkage coefficient (%);FSP = fiber saturation point (%).Were made dispersion graphics using volume shrinkage coefficients and dry density for linear correlation evaluation for 4 cases:• Case 1: VSC = f(ρ0), for Cedrella sp.;• Case 2: VSC = f(ρ0), for Cassia ferruginea;• Case 3: VSC = f(ρ0), for Vataireopsis araroba;• Case 4: VSC = f(ρ0), for all Wood species.The obtained results were statically analyzed using Pearson Correlation with level of significance of 5% using software for statistical analysis R and Microsoft Excel. To validation of Pearson Correlation Test was realized the Anderson-Darling Normality Test. P-value more than level of significance of the data present Normal Distribution, and there is no linear correlation between properties studied in this research (for Liner Correlation Tests).
3. Results and Discussion
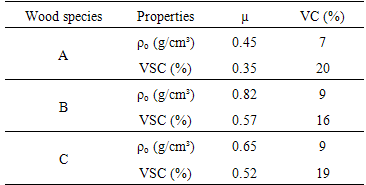
Table 1 present average values (µ) and variation coefficient (VC) to dry density and volumetric shrinkage coefficient of three Wood species: (A) Cedrella sp., (B) Cassia ferruginea and (C) Vataireopsis araroba. Table 1. Average values and variation coefficient of dry density and volumetric shrinkage coefficient for the three Wood species
 |
| |
|
Figures 3 to 5 present graphics of correlation between two studied properties (VSC versus ρ0) for the cases 1 (Cedrella sp.), 2 (Cassia ferruginea) and 3 (Vataireopsis araroba).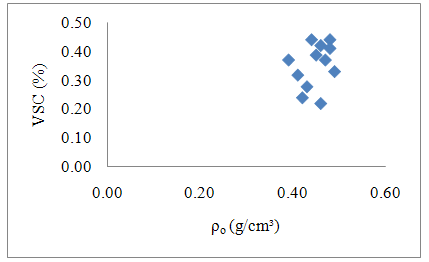 | Figure 3. Case 1 - Cedrella sp. |
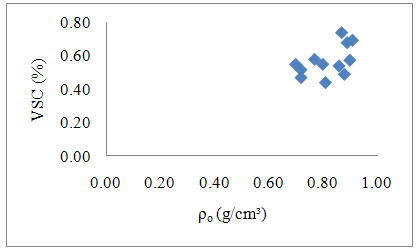 | Figure 4. Case 2 - Cassia ferruginea |
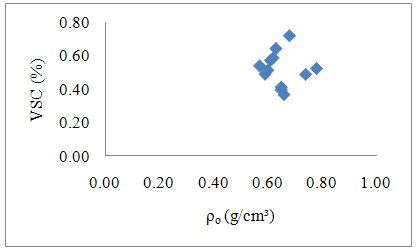 | Figure 5. Case 3 - Vataireopsis araroba |
Pearson Correlation Test was no-significant in the three cases (P-value > 0.05), or there is not linear correlation between dry density and volumetric shrinkage coefficient evaluating each specie separately.In an attempt to obtain a possible linear correlation between dry density and volumetric shrinkage coefficient, was performed graph of Figure 6, using datas of all Wood species (Case 4).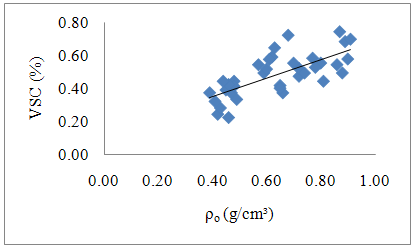 | Figure 6. Case 4 – All Wood species |
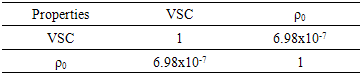
Table 2 present P-values of Pearson Correlation Test results using datas of the all Wood species, showed significance (P-value < 0.05). Note the existence of linear correlation between the properties, as shown by Kollman & Coté [6] for northern hemisphere Wood species.Table 2. P-values for Pearson Correlation Test – Case 4
 |
| |
|
Equation 4 is the one that best describes the relationship between the volumetric shrinkage coefficient and dry density, with a correlation coefficient (R²) equal to 0.520.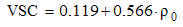 | (4) |
4. Conclusions
Based on the methodology employed and results obtained, it is possible to conclude that there is no linear correlation between the variables, oven dry density and volumetric shrinkage coefficient to separated Wood species: Cedrella sp., Cassia ferruginea and Vataireopsis araroba. Must highlight that, com full data, there linear correlation between dry density and volumetric shrinkage coefficient to trhee Brazilian tropical Wood species. To generalize the findings obtained here, further studies with larger number of species are necessary.
ACKNOWLEDGEMENTS
The Authors thank to Wood and Timber Structures Laboratory (LaMEM), Department of Materials Engineering (SMM), São Carlos Engineering School (EESC), São Paulo University (USP), by the materials and resources used in this research. Also, thank CNPq for financial supports.
References
| [1] | Calil Junior, C.; Lahr, F. A. R.; Dias, A. A,. Dimensionamento de elementos estruturais de madeira. 1 ed. Barueri: Manole Ltda, 2003. |
| [2] | Logsdon, N. B.; Calil Junior, C. Influência da umidade nas propriedades de resistência e rigidez da madeira. Cadernos de Engenharia de Estruturas, n.18, p.77-107, 2002. |
| [3] | Scaliante, R. M.; Almeida, D. H.; Macedo, L. B.; Macêdo, A. N.; Calil Junior, C. Ensaio de fluência e de compressão paralela às fibras para situações da madeira à umidade de equilíbrio e saturada. Madeira: Arquitetura e Engenharia, v.12, n.30, p.19-30, 2011. |
| [4] | Silva, D. A. L.; Lahr, F. A. R.; Faria, O. B.; Chahud, E. Influence of wood moisture content on the modulus of elasticity in compression parallel to the grain. Materials Research, v.15, n.2, p.300-304, 2012. |
| [5] | Galvão, A. P. M.; Jankowski, I. P. Secagem racional da madeira. São Paulo, Nobel, 1985, 112p. |
| [6] | Kollmann, F.; Cotê, W. A. Principles of wood science and technology. Germany, Springer Verlag, 1968, 592p. |
| [7] | Bodig, J.; Jayne, B.A. Mechanics of wood and wood composites. New York, Van Nostrand Reinhold Company, 1982, 712p. |
| [8] | Martins, V. A. Secagem de madeira serrada. Brasília, IBDF/DPq - LPF, 1988, 52p. |
| [9] | Oliveira, J. T. S.; Hellmeister, J. C.; Tomazello Filho, M. Variação do teor de umidade e da densidade básica na madeira de sete espécies de eucalipto. Revista Árvore, v.29, n.1, p.115-127, 2005. |
| [10] | Logsdon, N. B.; Finger, Z.; Penna, E. S. Caracterização físico-mecânica da madeira de Cedro-marinheiro, Guarea trichiliides L. (Meliaceae). Scientia Forestalis, v.36, p.43-51, 2008. |
| [11] | Logsdon, N. B. Sobre os ensaios de retração e inchamento. Madeira: Arquitetura e Engenharia, São Carlos, v. 1, n. 2, p.19-24, 1999. |
| [12] | Pliura, A; Yu, Q.; Zhang, S. Y.; Mackay, J.; Perinet, P.; Bousquet, J. Variation in wood density and shrinkage and their relationship to growth of selected young poplar hybrid crosses. Forest Science, v.51, n.5, p.472-482. |
| [13] | Korkut, S.; Guller, B. Physical and mechanical properties of European Hophornbeam (Ostryacarpinifolia Scop.) wood. Bioresource Techonology, v.99, p.4780-4785, 2008. |
| [14] | Sotannde, O. A.; Oluyege, A. O.; Adeogun, P. F.; Maina, S. B. Variation in wood density, grain and anisotropic shrinkage of plantation grown Azadiractha indic. Journal of Applied Sciences Research, v.6, n.11, p.1855-1861, 2010. |
| [15] | Batista, D. C.; Klitzke, R. J.; Taborda, C. V. S. Densidade básica e retratibilidade da madeira de clones de três espécies de Eucalyptus. Ciência Florestal, v.20, n.4, p.665-674, 2010. |
| [16] | Muñoz, G. R.; Anta, M. B. Physical properties of tinning wood in maritime pine (Pinus pinaster Ait.): case study. European Journal of Forest Research, v.129, p.1037-1045, 2010. |
| [17] | Kiaei, M. Anatomical, physical and mechanical properties of Eldas Pine (Pinus eldarica Medw.) grown in the Kelardasht region. Turkish Journal of Agriculture & Forestry, v.35, p.3-42, 2011. |
| [18] | Associação Brasileira de Normas Técnicas. ABNT NBR 7190: Projeto de estruturas de madeira. Rio de Janeiro: ABNT, 1997 |
| [19] | European Committee for Standardization. EUROCODE 5: Design of timber structures – Part 1 - 1: general rules and rules for buildings. Brussels: CEN, 2004. |
| [20] | Almeida, D. H.; Scaliante, R. M.; Christoforo, A. L.; Varanda, L. D.; Lahr, F. A. R.; Dias, A. A.; Calil Junior, C. Tenacidade da madeira como função da densidade aparente. Revista Árvore, v.38, p.203-207, 2014. |
| [21] | Christoforo, A. L.; Silva, S. A. M.; Panzera, T. H.; Lahr, F. A. R. Estimative of wooden toughness by the apparent density and bending strength. International Journal of Materials Engineering, v.4, p.49-55, 2014. |


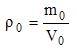
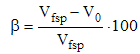
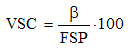




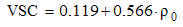
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML
