-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Materials Engineering
p-ISSN: 2166-5389 e-ISSN: 2166-5400
2014; 4(3): 103-113
doi:10.5923/j.ijme.20140403.06
Delamination Model Using Damage Mechanics Applied to New Composite for Orthopaedic Use
Djebbara Benzerga1, Abdelkader Haddi2, Antoine Lavie2
1Université des Sciences et de la Technologie Mohamed Boudiaf, Laboratoire Structures de Composite et Matériaux Innovants (LSCMI), Faculté de Génie, BP 1505 0ran El M’Naouer 31000, Algeria
2Univ Lille Nord de France, F-59000 Lille, France, Laboratoire Génie Civil et géo-Environnement (LGCgE), EA 4515, Faculté des Sciences Appliquées, Université d’ArtoisF-62400 Béthune, France
Correspondence to: Djebbara Benzerga, Université des Sciences et de la Technologie Mohamed Boudiaf, Laboratoire Structures de Composite et Matériaux Innovants (LSCMI), Faculté de Génie, BP 1505 0ran El M’Naouer 31000, Algeria.
| Email: |  |
Copyright © 2014 Scientific & Academic Publishing. All Rights Reserved.
In this study, delamination initiation and propagation are numerically predicted of a new laminated composite reinforced with natural organic load. This new composite is obtained from a laminated composite woven by incorporating a natural non-polluting organic load (granulates of date cores) which becomes hybrid composite. The new economical hybrid composite materialis made of an organic matrix containing methyl methacrylate, a woven reinforcement including a reinforcing glass fiber and a fabric perlon having an absorbing role. The walk cycle has been used to determine the operating conditions of tibiae prosthesis. Hence, the deflection tests were validated by orthopedist experts. This hybrid composite is used for the manufacture of composite for orthopaedic use and also for other applications in the future. The bonding conditions between layers are characterised by jumps in displacements which are proportional to the traction stresses. In order to describe the interface damage, an approach based on damage mechanics considering a softening stress-relative displacement law is presented. The objective is to develop a delamination model that can predict delamination growth in the new woven hybrid composite used in tibiae prosthesis. 3ENF tests were carried out on the new woven composite to detect delamination phenomenon. We assume that the interface has a bi-linear softening behaviour and regarded as being a whole of several interfacial bonds. Each bond is supposed to be made up of three stiffnesses acting in the three delamination mode directions. Numerical simulations are compared with experimental results carried out in single mode delamination tests, in the mixed-mode bending test to validate the delamination modeland in 3ENF test of a new woven laminated composite for orthopaedic use. A scalar damage variable is introduced and the degradation of the interface stiffness is established. The damage model is implemented into a commercial finite element ANSYS to simulate delamination in mode II. Numerical results on (90, 452, 0) are in good agreement with experimental observations.
Keywords: Composites materials, Interface, Damage, Delamination
Cite this paper: Djebbara Benzerga, Abdelkader Haddi, Antoine Lavie, Delamination Model Using Damage Mechanics Applied to New Composite for Orthopaedic Use, International Journal of Materials Engineering , Vol. 4 No. 3, 2014, pp. 103-113. doi: 10.5923/j.ijme.20140403.06.
Article Outline
1. Introduction
- Delamination is important phenomenon damage in the laminated composite materials due to weakness of reinforcement through the thickness. The study of the delamination of a laminate may be performed using an approach of fracture mechanics or by introducing appropriate constitutive laws of the interface between the layers constituting the laminate. From a physical point of view, it is reasonable to assume that the second approach can be related to fracture mechanics. In fact, when decohesion occurs between adjacent layers, there is evolution of delaminated surface which is equivalent to the propagation of a crack in a direction a priori known. The literature dealing with the phenomenon of delaminationis very large. A presentation of several structures subjected to the phenomenon of delamination, can be found [1-2]. The delamination phenomenon can be caused by concentration of interlaminar stresses that occur in the vicinity of the free edges or in around of the holes in laminated plates [3]. In addition, the interlaminar defects can grow under a compressive loading. In this case the thin laminated layers degrade (deboning interfaces) and are responsible for increased stresses in the vicinity of the boundaries of delaminated surfaces. In the analysis of the delamination can be distinguished the stage of the crack initiation from the phase of the crack propagation. For prediction of the initiation of a crack from a free edge, the technicalcal culations of the effect of the edge of elasticity [4-5], related to criteria based on the average of the normal stresses on a characteristic distance from the edge of the structure [6] are usually used in post- processor of an elastic design in laminated structures. Delamination does not occur necessarily where the stresses are highest. In the phase of the propagation of a delamination established, approaches based on the linear fracture mechanics are generally used. The rate of energy release G is a parameter that is often used to describe the behavior of the phenomenon of delamination in composite materials and structures. G is defined as the energy released from the newly fractured surface and compared to the critical value Gc (This method is used by many authors for the study of crack propagation [7-8]), but not treat the problem of the initiation of a delamination crack. In contrary the approach of the damage mechanics of the composite can describe the initiation of delamination. The rate of energy release is calculated from the forces and nodal displacements [9-10]. The state equations and the evolution laws of the interface provided in the context of thermodynamics are described in [11-17]. Models of elastic and damageable interface are presented in [18-22] and generalized in [23]. In these models, special interface elements are applied in areas where the delamination phenomenon is likely to occur. Elements plane strain with cubic interpolation functions were introduced for discretization of the laminate ply [24]. Other models have been developed for modeling damage layer [25] and interface phenomena [26]. These models are based on the damage mechanics. The interface is considered as a three-dimensional medium with negligible thickness compared to the other dimensions. Therefore, the interface can be considered as two-dimensional entity witch transfers traction and displacement from one layer to the other [27]. The interface is assumed to be dependent on the fibre orientation of adjacent layers and it is assumed to be elastic and damageable. Delamination may be caused by interlaminar stress [4]. The objective of this paper is to present a method to simulate progressive delamination based on a new mixed-mode failure criterion in the context of damage mechanics. This study will highlight the positive contribution of the powder core dates incorporated in the new woven composite. The date cores powder incorporation has an increase effect of the mechanical characteristics giving to the hybrid composite a better behaviour and reducing certain types of degradation like delamination.
2. Delamination Analysis
- It is widely recognised that the major contribution to delamination fracture resistance is given by the damage developing in matrix-rich interlaminar layer. Delamination is created by an important accumulation of cracks in the matrix. For this reason the delamination occurs in general later in the history of the laminate damage. Transverse matrix cracking, when it is propagated, can reach the interface between two layers of different fibre orientation. The interface between two adjacent layers can debond under inerlaminar tension stresses
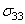 and/or shear stresses
and/or shear stresses 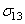 and
and 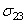 (figure 1).
(figure 1).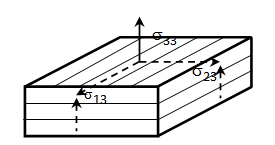 | Figure 1. Interlaminar stresses which cause delamination |
 | Figure 2. Interface: surface entity between two adjacent layers |
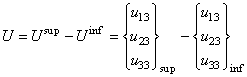 | (1) |
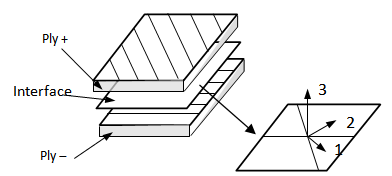
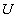 is the vector of relative displacements between two homologous points, which can be obtained from the displacements fields of the upper and lower surface.For damage caused in tension and shear through the thickness of the shell, the interface damage modelling is applied. This model allows the analysis of tests in fracture mechanics [31], from the method of determination of the parameters of the model. The mechanical behaviour of the interface depends only on the relative angle between the adjacent plies [32].The behaviour of the interface is assumed to be dependent on the fibre orientation of adjacent layers. This dependence can be taken into account by introducing a local reference frame of ‘natural’ orthotropic directions 1, 2 and 3; 3 is normal to the interface, 1 and 2 are the bisector of the angle formed by the fibres of the upper and lower layers (Figure 2) [33]. The constitutive equations between the interlaminar stresses and the displacement jumps in the orthotropic base of the interface are
is the vector of relative displacements between two homologous points, which can be obtained from the displacements fields of the upper and lower surface.For damage caused in tension and shear through the thickness of the shell, the interface damage modelling is applied. This model allows the analysis of tests in fracture mechanics [31], from the method of determination of the parameters of the model. The mechanical behaviour of the interface depends only on the relative angle between the adjacent plies [32].The behaviour of the interface is assumed to be dependent on the fibre orientation of adjacent layers. This dependence can be taken into account by introducing a local reference frame of ‘natural’ orthotropic directions 1, 2 and 3; 3 is normal to the interface, 1 and 2 are the bisector of the angle formed by the fibres of the upper and lower layers (Figure 2) [33]. The constitutive equations between the interlaminar stresses and the displacement jumps in the orthotropic base of the interface are 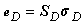 | (2) |
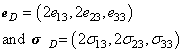
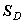 the constitutive matrix given in inverse form through the thickness such as
the constitutive matrix given in inverse form through the thickness such as 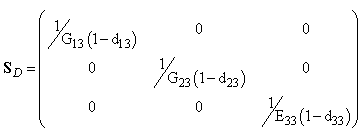 | (3) |
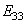 is the Young modulus through the thickness
is the Young modulus through the thickness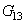 et
et 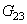 are the shear modulus in direction 1 and 2. The damage parameters
are the shear modulus in direction 1 and 2. The damage parameters 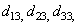 represent the shear and Young modulus reduction due to the interface damage. Delamination occurs in the thin layers between the plies of the composite. In delamination models, the stresses are assumed to be constant through the thickness t of the interface. By considering the classical relations deformation-displacements, the components of deformations in the thickness can be approached by
represent the shear and Young modulus reduction due to the interface damage. Delamination occurs in the thin layers between the plies of the composite. In delamination models, the stresses are assumed to be constant through the thickness t of the interface. By considering the classical relations deformation-displacements, the components of deformations in the thickness can be approached by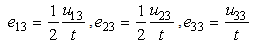 | (4) |
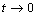
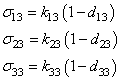 | (5) |
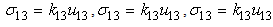 | (6) |
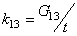 ,
, 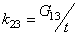 ,
, 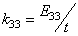 The relations (5) are the constitutive equations of an elastic and damageable interface. They link the normal and shear jumps through the interface to the stresses. The parameters of the interface damage
The relations (5) are the constitutive equations of an elastic and damageable interface. They link the normal and shear jumps through the interface to the stresses. The parameters of the interface damage 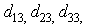 are three scalar damage variables which vary between 0 (no damage) and 1 (totally damaged).
are three scalar damage variables which vary between 0 (no damage) and 1 (totally damaged).3. Interface Damage Model
- It is assumed that the mechanical behaviour of the interface (
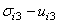 ) follows the law described in figure 3 where
) follows the law described in figure 3 where 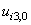 and
and 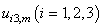 correspond to the displacements obtained for the maximum stress
correspond to the displacements obtained for the maximum stress 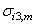 at the final rupture of the interface.
at the final rupture of the interface. 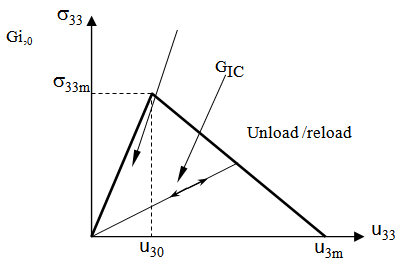 | Figure 3. Relation stress-relative displacement 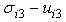 of the interface of the interface |
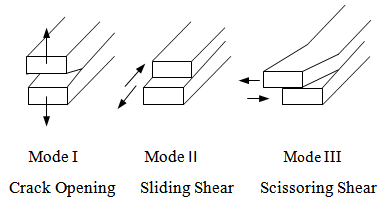 | Figure 4. Modes of delamination fracture |
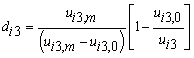 | (8) |
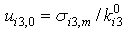
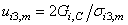 | (9a,b) |
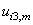 is the strain at zero stress or damage = 1 (propagation), and
is the strain at zero stress or damage = 1 (propagation), and 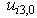 is the relative crack opening displacement at maximum stress or damage = 0 (initiation).According to [38], the function stress-displacement (5) has a triangular form (figure 3). The law of the damage evolution contains two parameters
is the relative crack opening displacement at maximum stress or damage = 0 (initiation).According to [38], the function stress-displacement (5) has a triangular form (figure 3). The law of the damage evolution contains two parameters 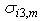 and
and 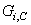 which is the critical energy of rupture or the work provided per unit of area for debonding of the interface. The interface initially elastic degrades gradually when the stress reached the value
which is the critical energy of rupture or the work provided per unit of area for debonding of the interface. The interface initially elastic degrades gradually when the stress reached the value 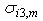 so that the energy of rupture in any mode is entirely absorbed at the separation [39, 17]. The interface is assumed to be made of several interfacial bonds and each bond is supposed to be constituted of three spring elements. Each element acts in one direction. The critical energies of rupture
so that the energy of rupture in any mode is entirely absorbed at the separation [39, 17]. The interface is assumed to be made of several interfacial bonds and each bond is supposed to be constituted of three spring elements. Each element acts in one direction. The critical energies of rupture 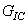 ,
, 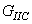 and
and 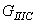 can be calculated as:
can be calculated as: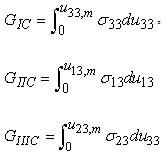 | (10) |
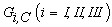 .In mixed mode of delamination analysis it is necessary to include simultaneously the three damage modes. To begin with, consider the stored energy function [41]:
.In mixed mode of delamination analysis it is necessary to include simultaneously the three damage modes. To begin with, consider the stored energy function [41]: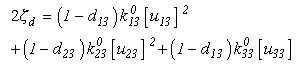 | (11) |
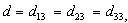 (the interface is a medium of very small thickness), Eq. (11) becomes
(the interface is a medium of very small thickness), Eq. (11) becomes 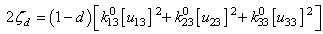 | (12) |
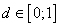 is the scalar damage variable. The work-conjugate of the damage variable follows from the classical thermodynamic argument as [42]:
is the scalar damage variable. The work-conjugate of the damage variable follows from the classical thermodynamic argument as [42]: 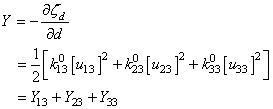 | (13) |
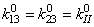 ), and assuming the delamination mechanisms in mode II and mode III to be same. Therefore, Mode III can be combined with Mode II by using a total tangential displacement
), and assuming the delamination mechanisms in mode II and mode III to be same. Therefore, Mode III can be combined with Mode II by using a total tangential displacement 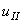 defined as the norm of the two orthogonal tangential relative displacements
defined as the norm of the two orthogonal tangential relative displacements 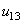 and
and 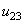 as
as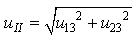 | (14) |
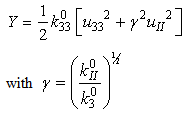 | (15) |
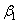 can thus be defined as:
can thus be defined as: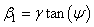 | (16) |
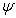 being the loading angle:
being the loading angle: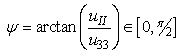 | (17) |
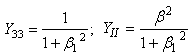 | (18) |
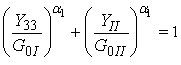 | (19) |
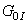 and
and 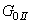 are the initial damage thresholds for a given loading angle (17) while
are the initial damage thresholds for a given loading angle (17) while 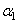 is positive model parameter. The initial mixed-mode threshold Y0 is computed from (19) as:
is positive model parameter. The initial mixed-mode threshold Y0 is computed from (19) as: 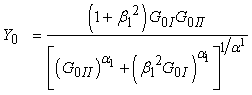 | (20) |
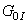 and
and 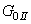 (fig.3) are recovered in the limit as
(fig.3) are recovered in the limit as 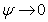 and
and 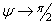 respectively.The criteria used to predict delamination propagation under mixed-mode loading conditions is generally established is terms of the energy release rates and fracture toughness. We use two criteria to predict the interaction of energy release rates in mixed mode. The first criterion is a power law [43], the second is B-K criterion [45], recently developed by Benzeggagh and Kenane.
respectively.The criteria used to predict delamination propagation under mixed-mode loading conditions is generally established is terms of the energy release rates and fracture toughness. We use two criteria to predict the interaction of energy release rates in mixed mode. The first criterion is a power law [43], the second is B-K criterion [45], recently developed by Benzeggagh and Kenane.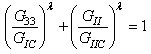 | (21) |
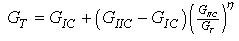 | (22) |
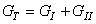 and
and  a parameter.The energies releases at failure are computed from (fig. 3):
a parameter.The energies releases at failure are computed from (fig. 3):  | (23) |
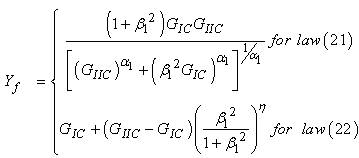 | (24) |
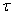
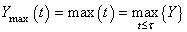 | (25) |
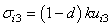 | (26) |
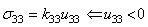 | (27) |
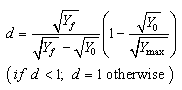 | (28) |
4. Element Formulation
- In this study the delamination has been modeled by the spring elements, COMBIN14. We assume that there is no friction between the lips of the crack (perfect sliding case) [46]. For each position on the crack front of the initial interface crack, the damage is calculated and compared with the critical value
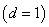 . When the damage is bigger the crack grows one step at the evaluated position and the spring element is disabled at this location. These ‘‘spring’’ elements, used for the elastic interface, have no thickness. This satisfies the condition of very thin interfacial zone comparatively to the dimensions of the constituents. For the numerical modeling the elastic interface was represented by a spring layer which resists normal extension and shear deformation (Fig. 5). A subroutine was developed and implemented into the FE code to model delamination growth simulation.
. When the damage is bigger the crack grows one step at the evaluated position and the spring element is disabled at this location. These ‘‘spring’’ elements, used for the elastic interface, have no thickness. This satisfies the condition of very thin interfacial zone comparatively to the dimensions of the constituents. For the numerical modeling the elastic interface was represented by a spring layer which resists normal extension and shear deformation (Fig. 5). A subroutine was developed and implemented into the FE code to model delamination growth simulation.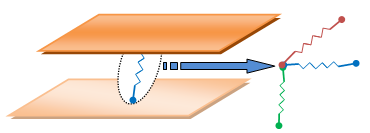 | Figure 5. Rheological representation of the interfacial bond based on the association of three springs |
5. Numerical Simulations
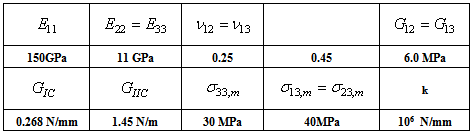
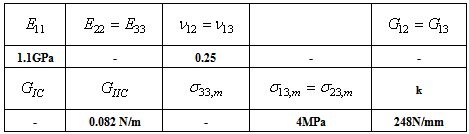
- Three test problems were selected to validate the proposed modelling. The first problem consists of the double cantilever beam (DCB) test used to determine Mode I toughness. Figure 6a shows displacement loading. The second problem modelled consists of the end-notched flexure test (ENF) used for Mode II toughness. The third test is the mixed bending mode test (MMB) with
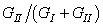 equal to 50%. All three of these problems have analytical solutions that were developed by Mi and Crisfield [47]. The geometry of test specimen composed of two plies is shown in table I and the proprieties of the composite in table II. Figures 6b, 7 and 8 show the numerical predictions and the experimental or analytical data for all the test cases simulated. A plot of reaction force as a function of the applied end displacement d is shown in Figure 6 for DCB tests. The load-deflection responses for the finite element model and the analytical prediction for 3ENF tests are shown in Figure 8. It can be observed that the comparisons of numerical simulations with experimental results are quite good. The load deflection curve calculated from FEM and beam solutions are shown in Figure 7. The beam solution assumes a linear interaction between the energy release rates. Reasonably good correlation is obtained among all three methods.
equal to 50%. All three of these problems have analytical solutions that were developed by Mi and Crisfield [47]. The geometry of test specimen composed of two plies is shown in table I and the proprieties of the composite in table II. Figures 6b, 7 and 8 show the numerical predictions and the experimental or analytical data for all the test cases simulated. A plot of reaction force as a function of the applied end displacement d is shown in Figure 6 for DCB tests. The load-deflection responses for the finite element model and the analytical prediction for 3ENF tests are shown in Figure 8. It can be observed that the comparisons of numerical simulations with experimental results are quite good. The load deflection curve calculated from FEM and beam solutions are shown in Figure 7. The beam solution assumes a linear interaction between the energy release rates. Reasonably good correlation is obtained among all three methods.
|
|
|
 | Figure 6a. DCB displacement loading |
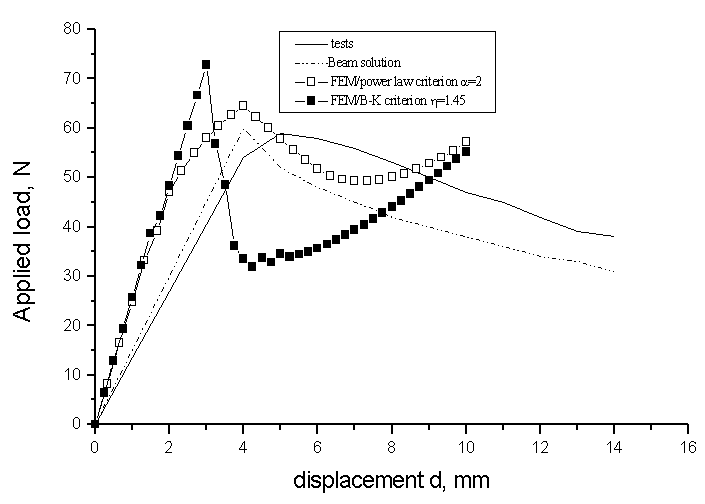 | Figure 6b. Load-deflection response of DCB test |
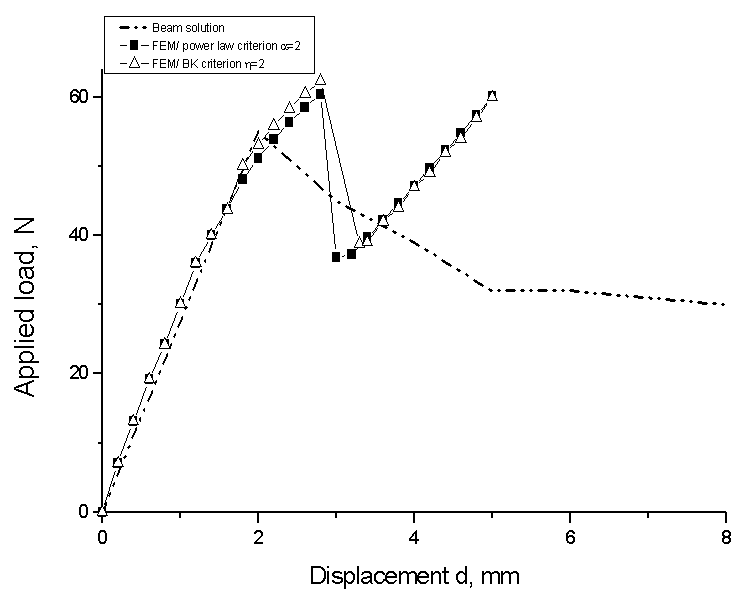 | Figure 7. Load-deflection response of MMB tests |
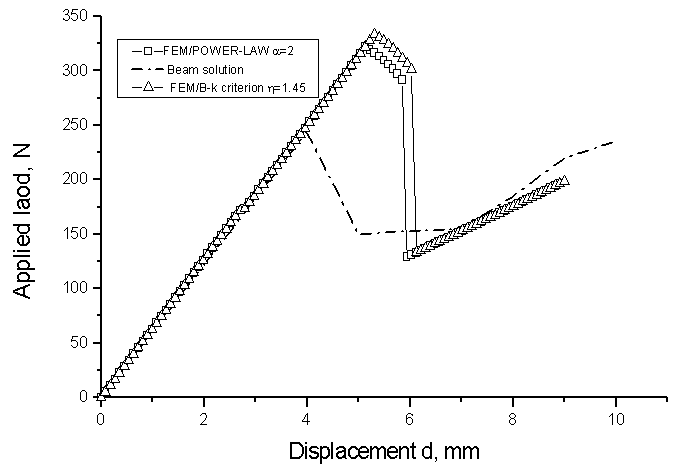 | Figure 8. Load-deflection response of 3ENF test |
6. New Woven Laminated Composite Debonding
- Hybrid composite: In addition to the components of the reference composite, a natural load: the date core pellet was built-in thus forming the hybrid composite. The date cores powder incorporation has an increase effect of the mechanical characteristics giving to the hybrid composite a better behaviour and reducing certain types of degradation like delamination. Fig. 9 shows homogenous and uniform date pellets distribution in the hybrid composite. It is necessary also to notice the phenomenon of date cores granulate intermingling around the fabric wicks. On figure 10, it appears fiber decoherence of glass fiber and illustrates the fiber rupture. We can see a consolidation due to date cores granulates. The fibers appear well intermingled. This phenomenon gives a better mechanical behaviour to the hybrid composite.
 | Figure 9. Micrograph of a polished area of one intermingled with fiber glass twill and granulated of date cores observed to MEB during the development of the hybrid composite [48] |
 | Figure 10. Fracture topography of hybrid composite [48] |
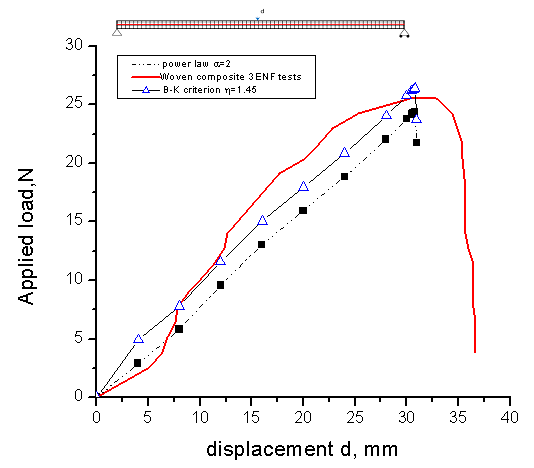 | Figure 11. Experimental and predicted curves of the woven laminated composite 3ENF tests |
7. Conclusions
- The version of this template is V1. Most of the formatting instructions in this document have been compiled by SAP Productions. SAP Productions offers A4 templates for Microsoft Word. SAP Productions has tried its best efforts to ensure that the templates have the same appearance a method for the simulation of progressive delamination based on spring elements was presented. Spring elements COMBIN 14 are placed between layers of solid elements that open and shear in response to the loading situation. The onset of damage and the growth of can be simulated without previous knowledge about the location, the size, or the direction of propagation of the delamination. A softening law for mixed-mode delamination that can be applied to any interaction criterion was proposed. The constitutive equation proposed uses thermodynamic conjugate forces variables, to track the damage at the interface under general loading conditions. The material properties required to define the element constitutive equation are the interlaminar fracture toughnesses, the penalty stiffness, and the strengths. The ENF test examples were presented that tests the accuracy of the method. Simulations of the ENF test represent cases of single-mode delamination. The examples analyzed are in good agreement with the analytical results and they indicate that the proposed formulation can predict the strength of composite structures that exhibit progressive delamination. The formulation can be extended to composite structures without any pre-existing defect. The new woven laminated composite for orthotropic use, debond problem was used as complex structure to test the capabilities of the method. The examples analyzed indicate that the method of interface considered as uniform distribution of springs is capable of accurately predicting delamination growth. This study shows also the positive effect of date cores powder incorporation on the mechanical characteristics giving to the new hybrid composite a better resistance and reducing delamination.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML