-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Materials Engineering
p-ISSN: 2166-5389 e-ISSN: 2166-5400
2014; 4(3): 92-96
doi:10.5923/j.ijme.20140403.04
Anisotropy Influence in Obtaining Stiffness Property in Bending of Brazilian Wood Species
Francisco Antonio Rocco Lahr 1, André Luis Christoforo 2, Tulio Hallak Panzera 3, Diogo Aparecido Lopes Silva 4, Decio Gonçalves 5
1Department of Structural Engineering, Engineering School of São Carlos (EESC/USP), São Carlos, 13566-590, Brazil
2Centre for Innovation and Technology in Composites – CITeC, Department of Civil Engineering, São Carlos Federal University, São Carlos, 13565-905, Brazil
3Centre for Innovation and Technology in Composites – CITeC, Department of Mechanical Engineering, Federal University of São João del-Rei, São João del-Rei, 36307-352, Brazil
4Department of Production Engineering, Engineering School of São Carlos (EESC/USP), São Carlos, 13566-590, Brazil
5Department of Civil Engineering, University of Franca (UNIFRAN), Franca, 14404-600, Brazil
Correspondence to: André Luis Christoforo , Centre for Innovation and Technology in Composites – CITeC, Department of Civil Engineering, São Carlos Federal University, São Carlos, 13565-905, Brazil.
| Email: |  |
Copyright © 2014 Scientific & Academic Publishing. All Rights Reserved.
The design of timber structures, and other materials, must follow the procedures and methods of calculation of normative standards. Some normative documents in the design of timber structures adopt quite simple arithmetical relationships to relate wood properties in order to make it simple and quick evaluation of the behavior of structural elements, as is the specific case of Brazilian standard ABNT NBR 7190:1997, establishing a single relation for the shear (G) and the longitudinal (E) modulus of elasticity [E=G/20], which implies taking statistical equivalence to the values of the elastic moduli in the longitudinal-radial (GLR) and longitudinal-tangential (GLT) directions, which are important properties in relation to the requirements of structural projects. In this context, this study aimed to investigate, with the aid of four and three points static bending tests performed on the of dicotyledonous wood species grown in Brazil, the determination of the values of ELR, ELT, GLR and GLT to confirm the possibility of its equivalence (ELR and ELT, GLR and GLT), and for establishing correlations among them. The results of the hypothesis testing between the shear and longitudinal modulus of elasticity exhibited equivalent by species and simultaneously for all species, and the results of the linear regression model showed not possible to estimate the shear modulus of elasticity with knowledge of the longitudinal modulus of elasticity, and the optimal coefficient found by least squares method to the relation between the modulus of elasticity was equal to 35 (E=G/35), suggesting the need for an adjustment of the coefficient for this scale more safe wooden structures.
Keywords: Wood, Modulus of elasticity, Bending, Anisotropy
Cite this paper: Francisco Antonio Rocco Lahr , André Luis Christoforo , Tulio Hallak Panzera , Diogo Aparecido Lopes Silva , Decio Gonçalves , Anisotropy Influence in Obtaining Stiffness Property in Bending of Brazilian Wood Species, International Journal of Materials Engineering , Vol. 4 No. 3, 2014, pp. 92-96. doi: 10.5923/j.ijme.20140403.04.
1. Introduction
- Improve design quality of building wooden elements and of timber structures is a goal that must be systematically sought by professionals working in the area.One of the main topics that can compete directly for this to be achieved is related to a deeper knowledge of strength and stiffness wood properties.Some normative standards in this subject adopt simple arithmetic relationships to relate wood properties in order to make simple and quick the evaluation of structural elements behavior. In the specific case of the Brazilian Standard ABNT NBR 7190:1997, some relations between longitudinal modulus of elasticity (E) and shear modulus (G) in wood are adopted, but without appropriate experimental basis. This can induce to doubts in engineering design and someone can take calculation assumptions that lead to overestimation of bars, resulting increase in structures cost, as asserted by Mateus [1], Karlsen [2]; Bodig and Jayne [3]; Ritter [4]; Calil et al. [5].To know the longitudinal and the shear modulus of elasticity is essential for correct evaluation of plate structures performance, for example, according to authors as Herzog et al. [6]; Christoforo et al. [7], Ferro et al. [8], Icimoto et al. [9], Braz et al. [10] among others.Several studies have been conducted to establish the theoretical basis aiming to determine shear modulus in wood, considering its features of orthotropy, being mentioned among them Price [11]; Schniewind [12], Gilles [13]; Holmberg, Persson, Petersson [14] and Nairn [15]. Each authors, with their specificities, have contributed to better understanding of the problem.Researchers like Ballarin and Nogueira [16]; Mascia and Rocco Lahr [17] sought to obtain experimental values of G, although working mostly with small number of specimens, aspect that prevent generalization of the results obtained.Christoforo et al.[18] presented an analytical methodology for determination the longitudinal and shear moduli of structural lumber, using the three-point static bending tests (adapted from Brazilian Standard ABNT NBR 7190 [19]), based on methodology recommended by Rocco Lahr [20]. Wood species used in these trials were Pinus elliottii and Corymbia citriodora. The related equations were developed according to virtual forces method and the shear shape coefficient (fs) to rectangular cross section was adopted as 1.20 (6/5). Results of coefficients (α) between moduli (E = α·G) for the referred wood species were, respectively, 18.70 and 21.20, very close to the coefficient (20) set by Brazilian Standard ABNT NBR 7190 [19].On the other hand, evaluations of strength and stiffness wood properties by non-destructive testing are becoming more frequent. Papers authored by Bucur and Archer [21], Sandoz [22], Ross, Brashaw and Pellerin [23]; Gonzales, Valle and Costa [24], Yang et al. [25]; Gonçalves, Trinca and Cerri [26], Alves and Carrasco [27], are some examples. However, often results constitute estimates based on correlation between parameters, with high variability among results.For simplicity, it has been usual to adopt statistical equivalence for values of G in the longitudinal-radial (GLR) and longitudinal-transversal (GLT) directions, important parameters related to structural design requirements, as evidenced by Gilles [13] and Green et al. [28], among others. Similar position is taken by the ABNT NBR7190 [19], that establishes a unique relationship between these properties, i.e., E = G/20.In this context, this work focuses on determining values of ELR, ELT, GLR and GLT, based on static bending tests (detailed in next items), to some dicotyledonous species grown in Brazil, aiming to confirm the possibility of consider its equivalence (ELR and ELT; GLR and GLT), and establish proper correlations.
2. Material and Methods
- To achieve the proposed objective, five hardwood species were considered, each one representing a strength class, according to establishes ABNT NBR 7190 [19]:- Cedinho (Erisma uncinatum), Class C20;- Peroba Rosa (Aspisdosperma polyneuron), Class C30;- Eucalipto Tereticornis (Eucalyptus tereticornis), Class C40;- Canafístula (Cassia ferruginea), Class C50;- Jatobá (Hymenaea stilbocarpa), Class C60.Note that including species in classes stipulated by ABNT NBR 7190 [19] is based on the characteristic values of compression strength parallel to grain.In this research, results of one set of twelve specimens (nominal dimensions 5cm×5cm×115cm) per species evaluated, obtained with the growth rings parallel to two opposite sides of specimens, were considered.Each specimen was tested four times in static bending: two with force applied on LR plane and two in the plane LT. In all situations, specimens were initially tested according to the four point static bending model (Figure 1a), used by American Standard ASTM D 198 [29], with nominal span 105 cm (L1), nominal height 5cm, obeying ratio L1/h≥21 [20] ensuring that shear stress contribution to vertical displacements (δ) is negligible. All tests were carried out non-destructively, restricting displacement at the midpoint of specimens to δ1 = L1/200. In this case, it is ensured that the proportionality limit was not exceeded [19].Once determined force (F1), responsible for displacement L1/200, and known specimens dimensions (height [h] and width [b] of cross section), these data are used in the equation of displacement for the above test structural model derived from the strength of materials (Equation 1), consisting of one equation with two unknown variables (E and G). Thereafter, the supports were approximated, giving a useful second length (L2) to the test piece (70cm), and this was applied to a load (F2) from the midpoint of the beam (Figure 1b), according three points static bending model. By holding the value of the scale and load displacement δ2 = L2/200 in the middle of the span of the structural model, these data were cast into Equation shifts from the strength of materials (Equation 2) providing a second equation in the variables E and G.
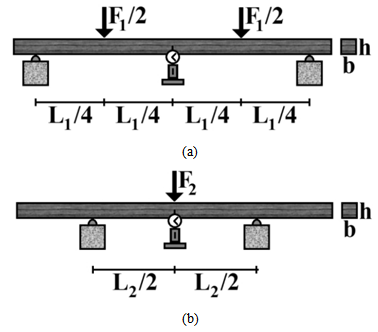 | Figure 1. Four point (a) and three points (b) static bending tests |
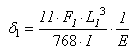 | (1) |
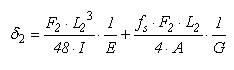 | (2) |
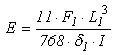 | (3) |
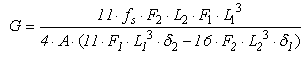 | (4) |
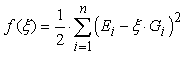 | (5) |
3. Results and Discussions
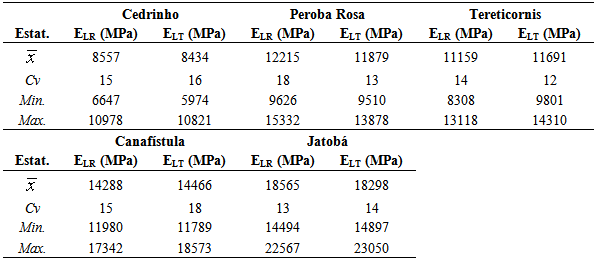
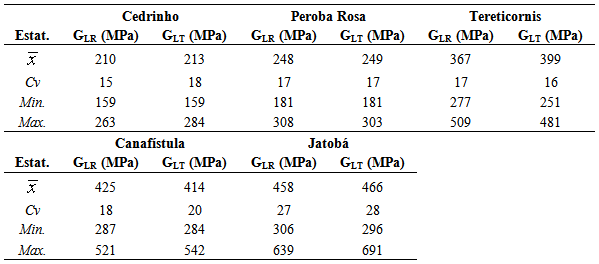
- Tables 1 and 2 present results of longitudinal modulus of elasticity and shear modulus, respectively, of the five wood species investigated; sample means (
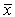 ); coefficients of variation (Cv); smallest (Min) and largest (Max) values found.
); coefficients of variation (Cv); smallest (Min) and largest (Max) values found.
|
|
|
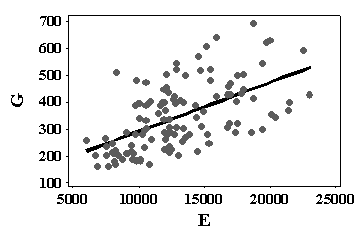 | Figure 2. Linear regression: G as function of E |
4. Conclusions
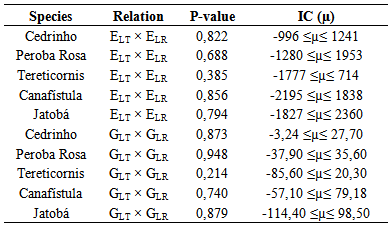
- Results of hypothesis tests between the modulus of elasticity ELR and ELT obtained based on static bending tests showed equivalence by species and for all species simultaneously.Results of linear regression by least squares show it is not possible to estimate shear modulus (G) by means of longitudinal modulus of elasticity (E). The best coefficient obtained by least squares model for the mentioned relation was 35 (G = E/35), 75% higher than coefficient (G = E/20) established by the Brazilian Standard ABNT NBR 7190 [19]. This suggests the need of adjusting coefficient E/G for the adequate design of timber structures.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML