1. Introduction

Use of wood from reforestation areas, as structural elements, has been disseminated in Brazil[1]. Availability of this material associated with new technologies contributes to increase its use in structures, with emphasis on rural buildings. In this sector, lumber and round timber (in natural or profiled shapes) can be employed.

Round pieces represent one of the most effective uses of forest resources, once require minimal processing between tree cutting and timber commercialization[2]. Pieces are peeled, dried and receive a preservative treatment before structural application. This product can be used in bridge, silos, containing structures, utility distribution lines, foundations, housing and so, as pointed out by Wolfe and Moody[3]; Wolfe and Kluge[4] and Zangiácomo[5].

Brazilian Code ABNT NBR 7190[6] specifies round timber considering their top and base diameters, regardless of species. The same document states that properties of strength and stiffness are obtained from tests on clear specimens. But researchers as Zangiácomo[5] argue that it is appropriate to adopt tests in structural dimensions pieces, once they can better represent the material.

Specimens proposed by ABNT NBR 7190[6] to obtain strength and stiffness wood properties in static bending present nominal dimensions 5cm×5cm×115cm. Tests must be carried out with 105cm nominal span, resulting ratio between length (L) and cross section width (h) equal to 21.

Ratio L/h≥21 was obtained by Rocco Lahr[7], using three point static bending tests on clear wood specimens. Tests carried out on the same piece (nondestructive) differed only by successive supports approximation, allowing investigating the influence of relationships L/h on modulus of elasticity values, obtained from Equation 1, which take in account only normal stresses in bending (Euller-Bernoulli Theory). In the Equation 1, δ is the displacement at span in midpoint; F the applied force; L the span between supports; MOE is the modulus of elasticity and I the moment of inertia of the cross section.

(1)

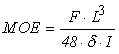Values of modulus of elasticity obtained from Equation 1 showed convergent for L/h ≥21 (Figure 1) and different for lower ratios (here titled apparent modulus of elasticity). This result ensures that contribution of displacements decurrent from shear stresses in static bending test can be neglected, when L/h≥21, in MOE calculation. So, the model (Euler-Bernoulli Theory), adopted by ABNT NBR 7190[6] for determining modulus of elasticity in static bending, can be considered valid, as pointed by Calil et al.[8], Ferro et al.[9], Icimoto et al.[10], Christoforo et al.[11] and Braz et al.[12].

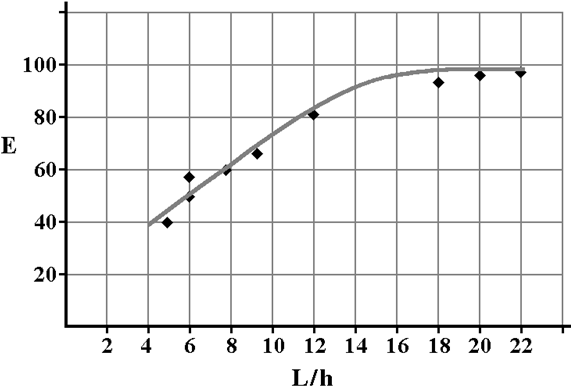Figure 1. L/h relationships. Adapted from Rocco Lahr[7]

In Brazil, codes related to round timber bars[13-17] are, for more than a decade, awaiting technical review[1]. Characterization studies involving timber poles generally took in account calculation methods contained in normative documents and have not focused proper dimensions ratios for justify using beams theory able to furnish the real modulus of elasticity of wood, as asserted by Zangiácomo [5].

This study aimed to determine, through three-point static bending tests: influence of the ratio between length and diameter (measured at the point of force application) of round timber bars; and ratio L/h from which it is possible to consider negligible the effect of displacements caused by shear stresses in the modulus of elasticity, employing the equation adopted by Brazilian Code ABNT NBR 7190[6].

2. Material and Methods

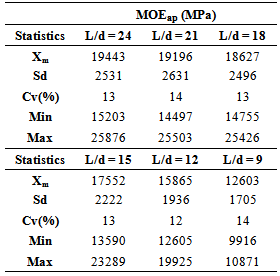
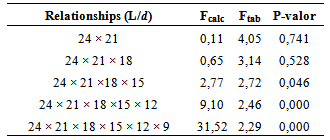
Poles of Corymbia citriodora, chosen because derived from reforestation areas, were donated by company IRPA, São Carlos, Brazil (24 pieces). Poles, 25 years old, presented length of 750cm; medium diameter 30cm; density 0,90g/cm³; moisture content about 15%; and conicity 1cm/m.

Tests to reach work’s aim were conducted in Wood and Timber Structures Laboratory (LaMEM), Structural Engineering Department (SET), São Carlos Engineering School (EESC), University of São Paulo (USP). Methodology to obtain MOE in different L/d ratios was based on Rocco Lahr[7], who employed three-point static bending tests, obtaining L/d 24, 21, 18, 15, 12 and 9, compounding six conditions for each pieces and one hundred forty four tests.

To ensure physical and geometric linearity, non-destructive tests (NDT) were carried out and displacements at mid-span were restricted to L/200, as required by ABNT NBR 7190[6] to check the limit state for bi-supported beams.

To verify the equivalence or not between the mean values of elastic moduli obtained from L/d relationship investigated were used hypothesis tests, with a significance level (α) of 5% (95% confidence), performed with the aid of Minitab software, version 14. If, for the degrees of freedom and significance level the parameter F_calc (F calculated) obtained from the software is less than the tabulated parameter F_tab, supports the null hypothesis (H₀: the population means are equal), or if the P-value is less than the significance level α, reject the null hypothesis[17].

3. Results and Discussions

Table 1 presents: mean values (X_m); standard deviations (Sd); coefficients of variation (Cv); maximum (Max) and minimum (Min) of the apparent modulus of elasticity (MOE_ap) for each L/d investigated.

Table 1. Apparent modulus of elasticity for the six l/d relationships

Figure 2 illustrates force versus displacement diagram for one tested round piece. Each line corresponds to a ratio L/d investigated.

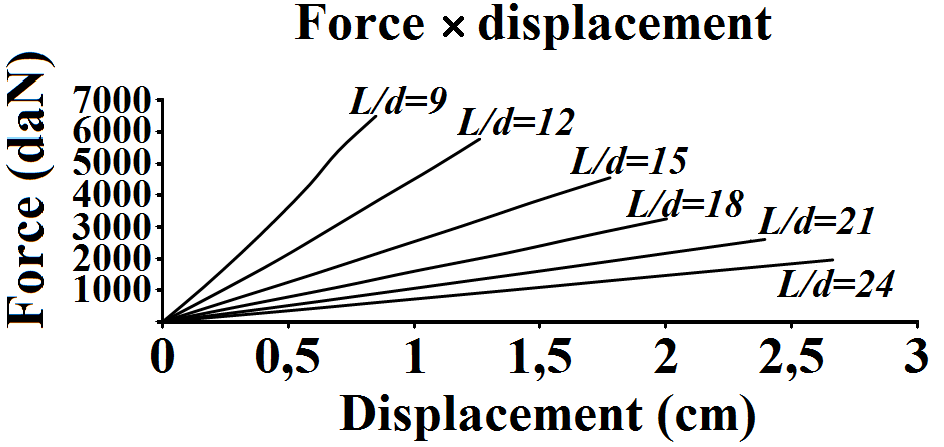Figure 2. Diagram force×displacement of a structural round piece for the L/d ratios

Fig. 3 shows graphic of apparent modulus of elasticity obtained for each ratio L/d.

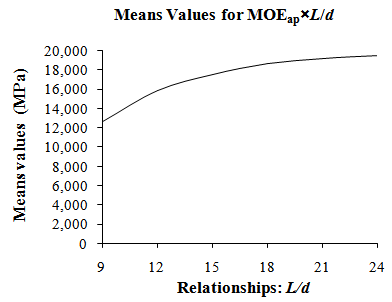Figure 3. Mean values of apparent modulus of elasticity versus L/d relationships

Table 2 present results corresponding to hypothesis tests over apparent modulus of elasticity obtained for different L/d ratios.

Table 2. Results of the hypothesis test for the modulus of elasticity between the l/d relationships

Graphic in Fig. 3 shows MOE_AP values very close when L/d reaches 18, with reduction of the slope of straight line that contain the means.

Results presented in Table 2 show that the means are statistically equivalent, at a significance level of 5%, to L/d = 24, 21, and 18. In this case, F_calc are inferior to F_tab, and P-values greater than 0.05. When, in analysis, means corresponding to L/D = 15, 12 and 9 were inserted, F_calc became superior to F_tab, with P-values less than 0.05. This indicates non-equivalent data. Thus, L/d = 18 is the lowest ratio, among the investigated, responsible for turning non-significant the influence of displacements decurrent of shear stress in bending tests.

4. Conclusions

Results found in this research showed valid to use Equation 1 only for relations L/d ≥18, close ratio to the obtained by Rocco Lahr[7] to lumber (L/h ≥21). This implies that, within the limit of the cited ratio L/d, three-point static bending test is able to determine modulus of elasticity once is truly negligible influence of displacements decurrently of shear stress, in these conditions.

Finally, it must be registered that to determine displacements (δ) in bending bars, when L/d≤18, it’s indispensable apply equations that consider δ as function of the modulus of elasticity (MOE) and the shear modulus (G).