| [1] | Christoforo, A. L.; Rocco, F. A. L; Morales, E. A. M.; Zangiácomo, A. L.; Panzera, T. H. Influence of Displacements on Calculus of the Longitudinal Modulus of Elasticity of Pinus Caribaea Structural Round Timber Beams. International Journal of Agriculture and Forestry, v. 2, p. 157-160, 2012. |
| [2] | Christoforo, A. L.; Panzera, T. H.; Batista, F. B.; Borges, P. H.; Rocco, F. A. L. Numerical evaluation of the longitudinal modulus of elasticity in structural round timber elements of Eucalyptus genus. Revista Engenharia Agrícola, v. 31, p. 1007-1014, 2011. |
| [3] | Associação Brasileira de Normas Técnicas (ABNT). NBR 7190. Projeto de Estruturas de Madeira. Rio de Janeiro, 1997. |
| [4] | Pigozzo, J. C.; Pletz, E.; Lahr, F. A. R. Aspectos da classificação mecânica de peças estruturais de madeira. Anais In: VII Encontro Brasileiro em Madeiras e em Estruturas de Madeira, São Carlos, SP, 2000. |
| [5] | Fiorelli, J.; Dias, A. A.; Coiado, B. Propriedades mecânicas de peças com dimensões estruturais de Pinus spp: correlação entre resistência à tração e classificação visual. Revista Árvore (Impresso), p. 741-750, 2009. |
| [6] | Miotto, J. L.; Dias, A. A. Produção e avaliação de vigas de madeira laminada colada confeccionadas com lâminas de Eucalipto. Revista Tecnológica, Edição Especial ENTECA, p. 35-45, 2009. |
| [7] | Ross. R. J.; Brashaw, B. K.; Pellerin, R. F. Nondestructive evaluation of wood. Forest Products Journal, v. 48, n. 1, p. 14-19, 1998. |
| [8] | Erikson, R. G.; Gorman, T. M.; Green, D. W.; Graham, D. Mechanical grading of lumber sawn from small-diameter lodgepole pine, ponderosa pine, and grand fir trees from northern Idaho. Forest Products Journal, v. 50, n.7-8, p. 59-65, 2000. |
| [9] | Oliveira, F. G. R.; Sales, A. Ultrassonic measurements in Brazilian hardwood. Materials Research, v. 5, n. 1, p. 51-55, 2002. |
| [10] | Miná, A. J. S.; Oliveira, F. G. R.; Calil Jr., C.; Dias, A. A.; Sales, A. Avaliação não destrutiva de postes de madeira por meio de ultrassom. Scientia Forestalis, n.65, p. 188-196, 2004. |
| [11] | Wang, S. Y.; Chen, J. H.; Tsai, M. J.; Lin, C. J.; Yang, T. H. Grading of softwood lumber using non-destructive techniques. Journal of Materials Processing Technology, v. 208, p. 149-158, 2008. |
| [12] | Liang, S.; Fu, F. Comparative study on three dynamic modulus of elasticity and static modulus of elasticity for Lodgepole pine lumber. Journal of Forestry Research, v. 18, p. 309-312, 2007. |
| [13] | Dong, X. H.; Hai, W. L. Comparative study on four different methods for measuring the dynamic modulus of elasticity of Acer mono wood. Advanced Materials Research, v. 160-162, p. 384-388, 2011. |
| [14] | Sales, A.; Candian, M.; Cardin, V. S. Evaluation of the mechanical properties of Brazilian lumber (Goupia glabra) by nondestructive techniques. Construction and Building Materials, v. 25, n. 3, p. 1450-1454, 2011. |
| [15] | Rocco Lahr, F. A. Sobre a determinação de propriedades de elasticidade da madeira. Tese de Doutorado, 216 p., Engenharia de Estruturas. Escola de Engenharia de São Carlos, Universidade de São Paulo, São Carlos, 1983. |
| [16] | Burdzik, W. M. G.; Nkwera, P. D. Transverse vibration tests for prediction of stiffness and strength properties of full size Eucalyptus grandis. Forest Products Journal, v. 52, n. 6, p. 63-67, 2002. |
| [17] | Zangiácomo. A. L; Rocco Lahr, F. A. Avaliação do efeito do cisalhamento na flexão de elementos roliços da espécie Eucalyptus Citriodora. Anais In: XI Encontro Brasileiro em Madeiras e em Estruturas de Madeira, Londrina-PR, 2008. |
| [18] | Christoforo, André Luis; Icimoto, F. H.; Fernandes, C. V.; Fiorelli, J.; Negrao, J.; Rocco, F. A. L. Shear and Longitudinal Modulus of Elasticity in Structural Profiled Round Timber Beams. International Journal of Materials Engineering, v. 3, p. 87-91, 2013. |
| [19] | Christoforo, A. L.; Ribeiro Filho, S. L. M.; Panzera, T. H.; Rocco, F. A. L. Metodologia para o cálculo dos módulos de elasticidade longitudinal e transversal em vigas de madeira de dimensões estruturais. Ciência Rural (UFSM. Impresso), v. 43, p. 610-615, 2013. |
| [20] | American Society for Testing and Materials (ASTM). Standard test method of static tests of lumber in structural sizes. ASTM D-198. Annual book of ASTM standards, v. 03.01. ASTM, West Conshohocken, Philadelphia, 1997. |
| [21] | Sanches Jr., F.; Venturini, W. S. Damage modeling of reinforced concrete beams. Advances in Engineering Software, v. 38, n. 8-9, p. 538-546, 2006. |
| [22] | Timoshenko, S. P. Strength of materials - Part 1. Second edition, D. Van Nostrand Company, Inc., New York, pp. 170-171, 1940. |
| [23] | Mindlin, R. D.; Deresiewicz, H. Timoshenko´s shear coefficient for flexural vibration of beams. Technical Report, no.10, ONR Project NR064-388, Department of Civil Engineering, Columbia University. New York, 1953. |
| [24] | Roark, R. J. Formula for stress and strain. Third edition, McGraw-Hill Book Company, Inc, New York, pp. 119-121, 1954. |
| [25] | Christoforo, A. L.; Rocco, F. A. L.; Morales, E. A. M.; Panzera, T. H.; Borges, P. H. Numerical Evaluation of Longitudinal Modulus of Elasticity of Eucalyptus grandis Timber Beams. International Journal of Agriculture and Forestry, v. 2, p. 166-170, 2012. |
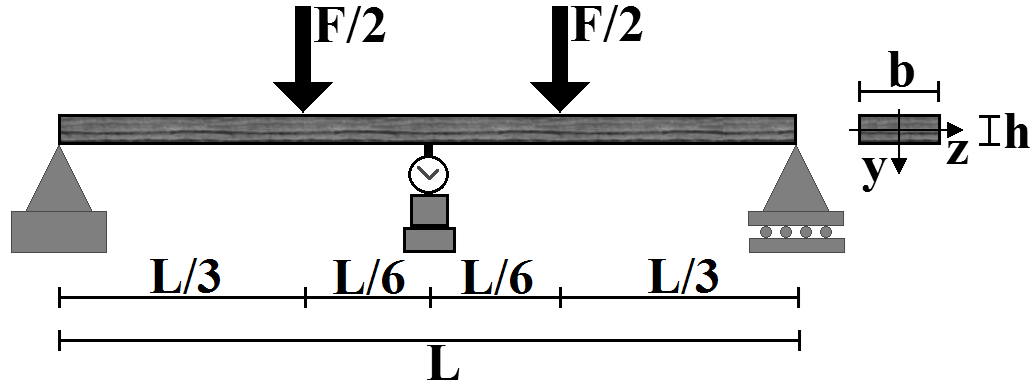
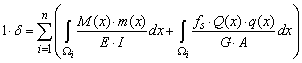
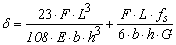
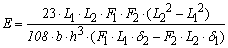
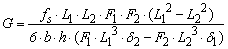
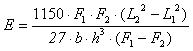
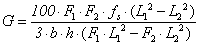
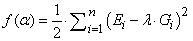
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML