Sihem Abidi1, Habib Sammouda1, Rachid Bennacer2
1LabEM, LR11ES34- Université de Sousse, Ecole Supérieure des Sciences et de Technologie, Rue Amin ElAbbassi, 4011 Hammam Sousse, Tunisie
2ENS-Cachan, LMT, Dpt GC 61, Av. Président Wilson 94235 Cachan Cedex, France
Correspondence to: Sihem Abidi, LabEM, LR11ES34- Université de Sousse, Ecole Supérieure des Sciences et de Technologie, Rue Amin ElAbbassi, 4011 Hammam Sousse, Tunisie.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
Hybrid photovoltaic thermal sensors exploit heat energy modules for space heating while increasing overall conversion yield. They have several advantages over classic sensors, including ease of integration with the facades of the buildings or on the roof, and an improved total efficiency of conversion of solar radiation. Photovoltaic modules based on silicon crystalline are increasingly used in embedded systems. To improve the performance of the hybrid photovoltaic / thermal system, a new heat exchanger of three coolants, two fluids and one solid, is associated with a solar photovoltaic panel cells, our study focuses on the determination of the thermal and electrical performance of photovoltaic thermal hybrid sensor, which is covered with an additional pane above the conventional module; we determined the distribution of the temperature at each point of the hybrid sensor. The result of this study will permit to optimize the values of characteristic numbers, Ra, Lpm (width of the area between PV panel and material), Em (thickness of the absorber metal) and the thermal conductivity of the solid absorber.
Keywords:
Convection, Heat Exchanger, Sensor Solar PV Cells, Coolant
Cite this paper: Sihem Abidi, Habib Sammouda, Rachid Bennacer, Thermal Study of a Covered and Hybrid Photovoltaic Sensor Associated with a Heat Exchanger, International Journal of Materials Engineering , Vol. 3 No. 6, 2013, pp. 113-123. doi: 10.5923/j.ijme.20130306.01.
1. Introduction
Many researches towards the solar energy occur all over the world due to the concern of global crisis on oil and gas prices. According to Deffeyes[1] and later, Bardi[2], oil has already started to peak. Sadorsky[3] mentioned that oil prices are often indicative of inflationary pressure in the economy which in turn could indicate the future of interest rates and investments, gas and coal reserves, which are larger than oil; it will later tend to be progressively replaced by the former, which should attenuate a price explosion. Pareto[4] mentioned that this process will push energy prices higher, until sustainable sources replace dependency on fossil fuels as major source of energy. Constatntinos and Bouroussis[5] mentioned that the sustainable energy such as solar energy in a form of solar radiation has been identified as one of the promising source of energy to replace the dependency on other energy resources. The global need for energy savings requires the use of renewable sources in many applications. One of the renewable sources of energy is the photovoltaic solar energy (PV). As revealed by Tripanagnostopoulos[5], hybrid photovoltaic/thermal system in the other hand is the continuity of the photovoltaic solar energy system, it combined both systems into one system known as hybrid photovoltaic/thermal (PV/T or PVT) solar system. A.Ibrahim et al.[6] compared each type of flat plate PV/T collectors on its design and performance. Basak. K.k et al.[7] presented a comparison of Trombe wall system between a single glass PV panel and another with a double glass. After validation of the numerical models with the experimental results, these systems will be used in a building in different climatic conditions, glass types and thermal masses. Furthermore, they noted that the temperature reached by PV cells is higher than the ambient temperature and that the efficiency of PVTs is greater than the combined sum of separate PV and thermal collectors. In the light of this, they suggest that PVT systems offer a cost effective solution for applications where roof area is limited. D. Kamthania et al. [8] evaluated the performance of a hybrid PVT double pass façade for space heating in the composite climate of New Delhi by using a semi transparent PV module. Thermal modeling has been carried out based on the first and second law of thermodynamics in order to estimate the electrical and thermal energy along with the exergy for a “semi transparent” hybrid PVT double pass façade instead of an opaque PV panel. In this context, they suggested that the semi transparent PV module has more electrical efficiency than the opaque PV module. GL. Jin et al.[9] developed an experiment on a single-pass PV/T with a rectangular tunnel absorber. The rectangular tunnel which acted as an absorber collector has been fixed underneath the photovoltaic panel. The main purpose of the experiment is to identify a suitable air flow for cooling the PV panel. With this method, the efficiency of the panel will increase. The result showed that the combined PV/T efficiency was 64.72% and the thermal efficiency 54.70% with solar irradiance of 817.4Wm-2, and the mass flow rate reached 0.0287kgs-1 at ambient temperature of 25°C. They concluded that the hybrid PV/T with rectangular tunnel, as a heat absorber showed a higher performance compared to the conventional PV/T system. In Hong Kong, Chow et al.[10] carried out outdoormeasurements on two identical sheet-and-tube thermosyphon PVT/w collector systems, in which one, the collector was glazed. Together with a validated numerical model, the appropriateness of having front glazing was evaluated. The first law of thermodynamic evaluation indicates that the glazed design is always suitable whether the thermal or the overall energy output is to be maximized, but the exergy analysis supports the use of unglazed design if the increase of PV cell efficiency, packing factor, ratio of water mass to collector area and wind velocity are seen as desirable factors.The aim of this paper is to study the efficiency of the overall system (PV + exchanger) using steady values of characteristic numbers, Ra, Lpm (width of the area between PV panel and material), Em (thickness of the absorber metal) and λ (the thermal conductivity of the solid absorber). It was demonstrated that the optimum performance of the system must be both electrical (junction temperature of the PV) and thermal (temperature of the hot air recovered at the outlet of the channel).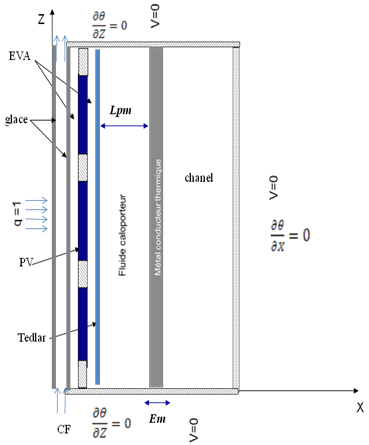 | Figure 1. geometric configuration |
2. Governing Equation
The movement of the fluids and their temperature are governed by continuity, momentum and energy equations in the solid and fluid phases. The heat flux imposed on the up boundary is considered only on the level of PV cells, with density q. The flow is considered to be steady, laminar and in two dimensions via a computational fluid dynamics technique. The thermo physical properties of the fluid are assumed to be constant, except for the density in the buoyancy term, which depends linearly on the temperature, i.e., the Boussinesq approximation is assumed to be valid. Thus, the reference variables for length, velocity and temperature are chosen respectively as: x=x*/H and z=z*/H, 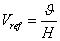 and
and 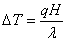 The dimensionless variables are:
The dimensionless variables are: 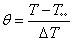 and
and 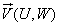 The dimensionless conservation equations of mass and momentum for the dimensionless natural convection flow of fluid are:v On the level of the fluid:
The dimensionless conservation equations of mass and momentum for the dimensionless natural convection flow of fluid are:v On the level of the fluid: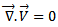 | (1) |
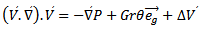 | (2) |
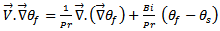 | (3) |
The above equations are related to the fluid.Eq. (3) involves the temperature of the solid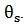 Thus, an energy equation should be written to determine
Thus, an energy equation should be written to determine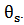 This equation reads:v On the level of the solid exchanger:
This equation reads:v On the level of the solid exchanger: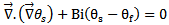 | (4) |
The problem is characterized by the classical Prandtl number, Pr, the Rayleigh number, Ra, the Biot number of each fluid, 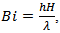 which takes the value zero away from interfaces.
which takes the value zero away from interfaces.
3. Boundary Conditions
at X = 0 : W = 0, U = 0 and 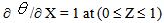 at X = A : W = 0, U = 0 and
at X = A : W = 0, U = 0 and 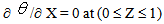 at Z = 1 :
at Z = 1 : 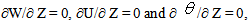 at the channel and W = 0, U = 0 and
at the channel and W = 0, U = 0 and 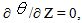 at the cavityat Z = 0 :
at the cavityat Z = 0 : 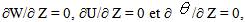 at the channel and W = 0, U = 0 and
at the channel and W = 0, U = 0 and 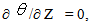 at the cavity
at the cavity
4. Results and Discussions
The governing Eqs. 1-4 with the boundary conditions were solved using the finite volume method. The computational domain is divided into rectangular control volumes with one grid point located at the centre of the control volume that forms a basic cell. The conservation equations are integrated in the control volumes, leading to a balance equation for the fluxes at the interfaces. A second order scheme is used to distinguish the equations; a false transient procedure is used in order to obtain a permanent solution. To accelerate the convergence, the SIMPLER algorithm, originally developed by Patankar[11], is coupled with the SIMPLEC algorithm of van Doormaal and Raithby [12] (see Bennacer[13]). Non uniform grids are used in the program, allowing fine grid spacing near the boundaries. Trial calculations were necessary to optimize the computation time and accuracy. Convergence with mesh size was verified by using coarser and finer grids for selected test problems. The convergence criterion is based on both the maximum error of continuity equation and the average quadratic residue over the whole domain for each equation being less than a prescribed value ζ (generally less than 10-6).The goal of the present study is to be interested in recovering waste heat by Joule effect by adding the sensor PV exchanger three coolants and demonstrating the optimum of performance of the system in both electrical (junction temperature of the PV) and thermal (temperature of the hot air recovered at the outlet of the channel). The heat quantity transferred, at position z, is calculated from the average Nusselt number, Nu (z), a long x direction, defined as: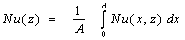 And the average Nusselt number,
And the average Nusselt number, 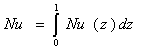 Where
Where 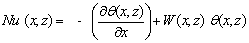 the local heat transfer at any point. Where W is the velocity component along Z axis.
the local heat transfer at any point. Where W is the velocity component along Z axis.
4.1. Validation of Numerical Model
The present numerical results are evaluated for accuracy against experimental results published in previous works[14]. Figure 2 shows the comparisons of the thermal and electrical efficiency of the system according to the ratio of the reduced temperature and global incident radiation on the collector surface between the results from our computer code and T.N.Anderson et al.[14] results. The comparisons of temperature and velocity profiles in the canal between the results from the present computer code and R. Ionut et al.[15] results are shown in Figure 3.Significant agreement is observed, which demonstrates the validity of the formulation and the computer code.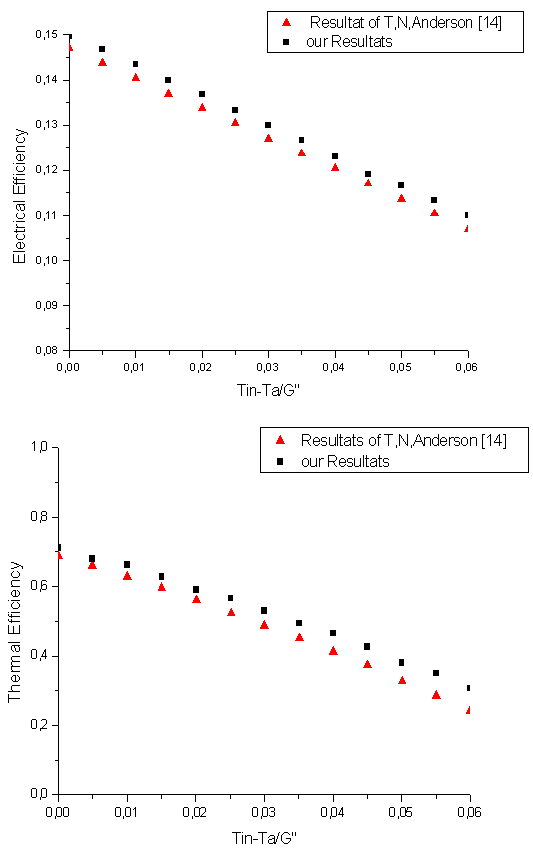 | Figure 2. Comparison of our results with those of T.N.Anderson et al.[14] for absorber conductivity |
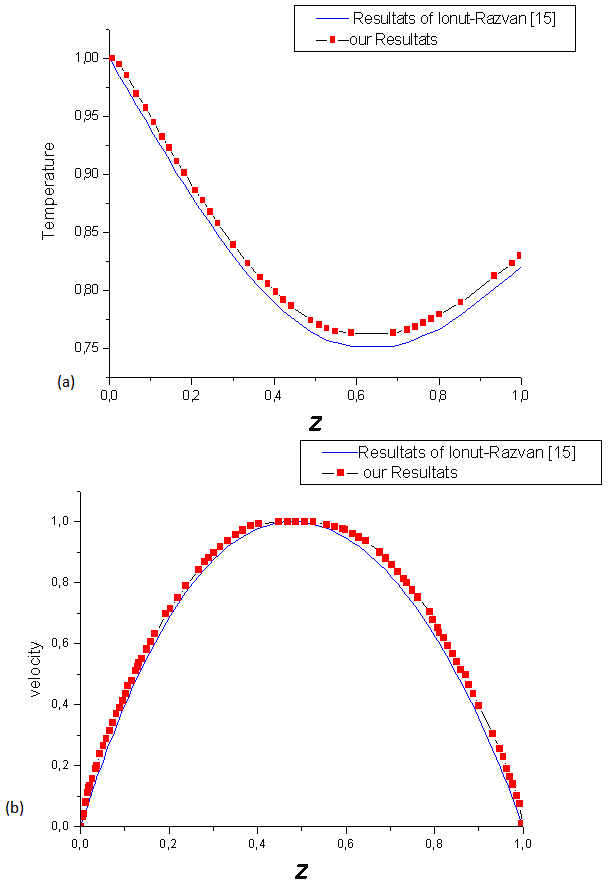 | Figure 3. Comparison of our results with those of R. Ionut-Caluianu et al.[15] with (a): temperature Profile in the middle of the channel and (b): speed Profile in the middle of the channel |
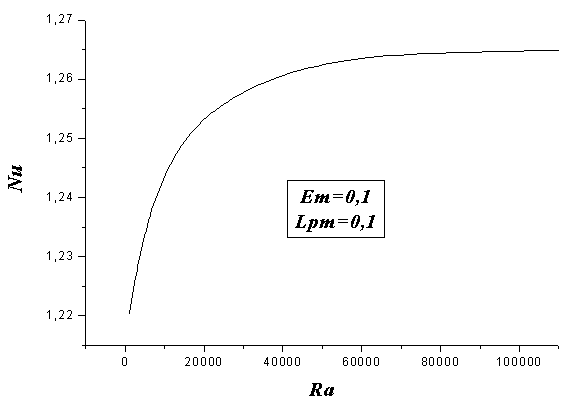 | Figure 4. Influence of the captured flux (ie Rayleigh number) on the thermal heat transfer: Lpm = 0.1, A = 1, Ra = 104, Em = 0.1 |
4.2. Parametric Analysis
√ Effect of heat flux capturedFig. 4 shows the evolution of the Nusselt number as a function of the heat flux received by the solar panel. When the heat flux increases, the convective fluid flow progresses. The consequence effect is showed through the evolution of the Nusselt number where the heat transfer is accelerated and the conductive mode is dominated by the natural convective one. This can be explained by the fact that the metal interface does not transmit heat to the channel with the same proportion as that transmitted from the PV cells to the fluid in the area between the PV panel and the material. √ Effect of the width of the area between PV panel and material; LpmFig. 5 shows the profiles of the vertical velocity for different widths of the area between the PV panel and the metal plate, Lpm. It was found that the variation in the horizontal mid-plane is sinusoidal and the fluid velocity increases for low values of Lpm, which means that the heat transfer is improved by reducing Lpm. In the range of solid sheets, it can be seen that there is no flow (zero speed), so that in the channel it is noted that the reduction in the width of the area between PV panel and material induces an increase in the speed, which means that the amount of movement of the fluid in the channel, and therefore the temperature gradients increased. Accordingly, we can say that the heat transfer is more important when reducing the width of the area between the PV panel and material Lpm.Fig. 6 shows the temperature profiles at two remarkable positions: the median plane of the area between the PV panel and material and the mid-plane of the channel for Ra = 105, A = 1, Em = 0.1 and for different values of Lpm, the width of the area between PV panel and material. It was found that for low values of Lpm, attenuation in temperature in the layer between the PV panel and material is observed. While in the channel it can be seen that the temperature becomes more significant when decreasing the width of the area between the PV panel and material. This explains the increase of the heat transfer towards the channel when decreasing Lpm.√ Effect of the thickness of the absorber metal, EmThe profiles of the vertical velocity for different metal thickness of the absorber are shown in Fig. 7. It was found that the variation in the horizontal mid-plane is sinusoidal and the fluid velocity increases for low values of Em, which means that the heat transfer is improved by reducing Em. In the range of the solid plate, it can be seen that there is no flow (zero speed). At the interface, a dynamic boundary layer flow is developed. Fig. 8 shows the temperature profiles at two remarkable positions: the median plane of the layer between the PV panel and material and the mid-plane of the channel for Ra = 105; Lpm = 0.1 and A = 1 and for different values of the thickness of the absorber metal, denoted Em We note that the effect of this relationship manifests itself in two ways.Near the bottom wall of the photovoltaic panel, we see that more Em decreases as the temperature value decreases in this area. In the mid-plane of the channel, we find that the greater the thickness of the absorber metal decreases as the temperature increases, at the level of this area. This explains why the heat transfer is more important for thin lines of metal absorber.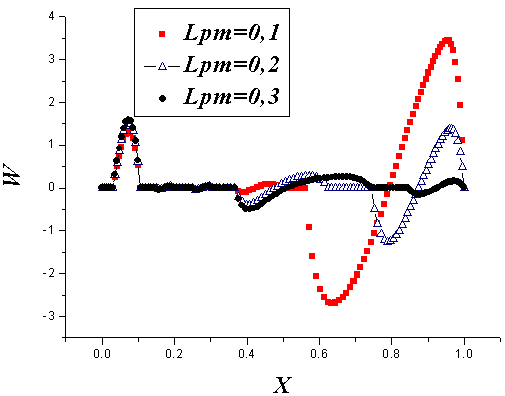 | Figure 5. Effect of the width of the area between PV panel and the metal plate on the profiles of the vertical velocity along the horizontal axis: A = 1; Ra = 105; Em = 0.1 |
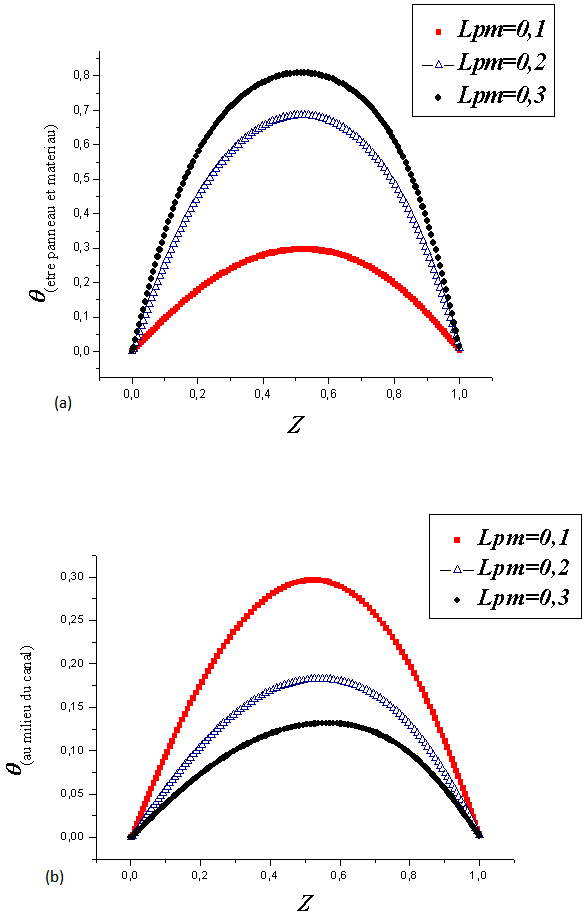 | Figure 6. Temperature profiles: (a) in the bottom wall of the sensor PV and (b) to the median plane of the channel for different Lpm with Ra = 105, A = 1, Em = 0.1 |
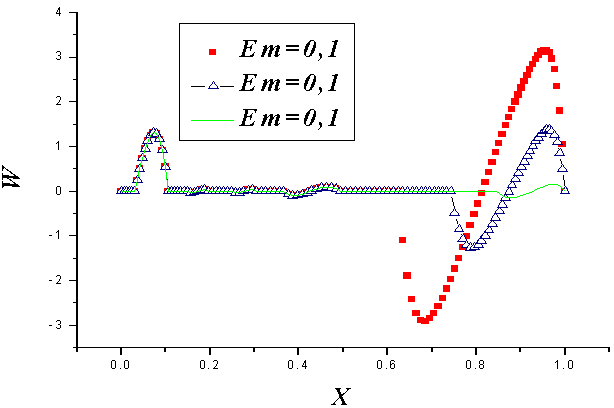 | Figure 7. Effect of the thickness of the absorber metal profiles of the vertical velocity along the horizontal axis: A = 1, Ra = 105, Lpm = 0.1 |
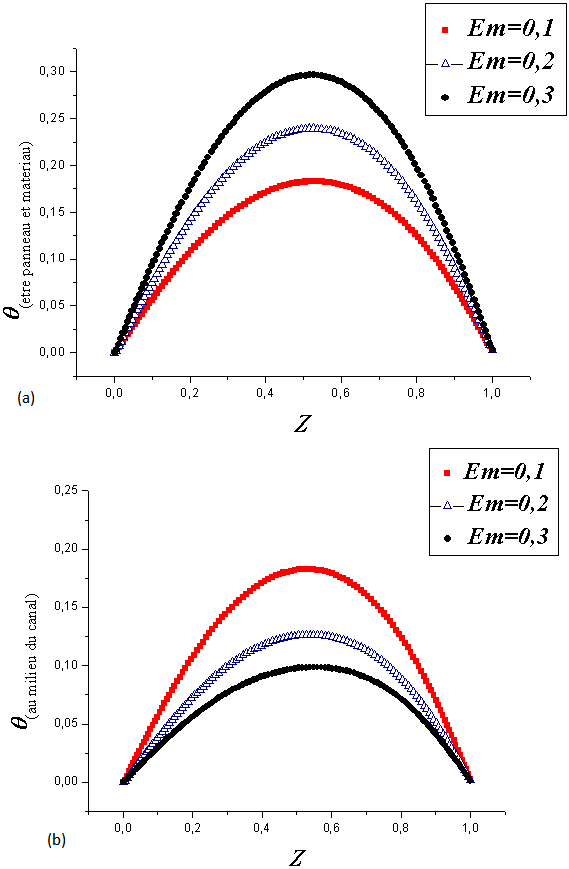 | Figure 8. Effect of the thickness of the absorber metal on the temperature profiles: (a) between the PV panel and material and (b) in the mid-plane of the channel for Ra = 105, A = 1, Lpm = 0.1 |
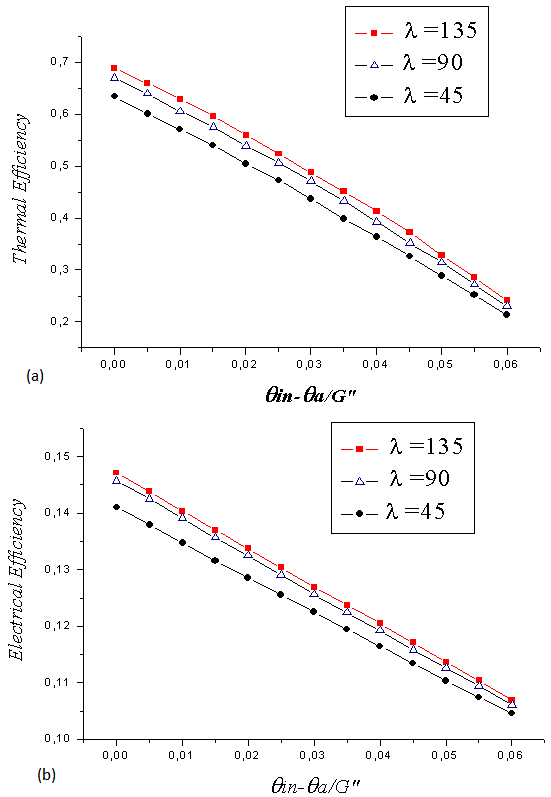 | Figure 9. Efficiency: (a) thermal and (b) electrical of system on the report of the reduced temperature and the radiation incident on the overall surface of the collector to different values of conductivity of the absorber solid: Lpm = 0.1, A = 1; Ra = 104, Em = 0.1 |
√ Effect of the solid absorber thermal conductivity In Fig. 9 (a) it can be seen that by increasing the value of the heat transfer coefficient to 135 W/m2K, the maximum thermal efficiency is improved by approximately 5%. Given that the high thermal conductivity adhesives are commonly used in attaching electrical components to heat sinks to improve cooling. It is evident that using them to attach the PV cells in the BIPVT would also improve the electrical efficiency. In Fig. 9 (b) it can be seen that by reducing the bond thermal resistance, there is a marked increase in the electrical efficiency. As such, it would be prudent to ensure that the thermal conductivity between these bodies is maximized. However, it should also be recognized that these results are asymptotic, suggesting other areas that are limiting the efficiency of the BIPVT. In addition to improving the heat transfer between the absorber and the PV cells, we may improve the optical efficiency of the BIPVT system by reducing the reflectance of the PV cells.
5. Conclusions
To improve the performance of the hybrid photovoltaic / thermal system, a new heat exchanger of three coolants, two fluids and one solid, is associated with a solar photovoltaic panel cells. This exchanger is formed of a cavity enclosing a first heat transfer fluid to high heat capacity with an open channel and a second driving heat exchanger (air), the wall adjacent to the cavity is an absorber solid high thermal conductivity. The aim of this work is to recover the maximum of waste heat by Joule effect by adding the sensor PV exchanger of three coolants which implies the improvement of the efficiency of such a system. The results show that the good choice of the fluid coolant in contact with the photovoltaic panel will make it possible to recover the maximum of heat released by Joule effect. In addition, the optimization of the thermal characteristics of the coolant solid is necessary to guarantee a good heat transfer such as the thermal conductivity. Finally, this study permitted to optimize the values of characteristic numbers, Ra, Lpm (width of the area between PV panel and material), Em (thickness of the absorber metal) and the thermal conductivity of the solid absorber. It was demonstrated that the optimum performance of the system must be both electrical (junction temperature of the PV) and thermal (temperature of the hot air recovered at the outlet of the channel).
Nomenclature

Greek letters

Subscripts

References
| [1] | Deffeyes KS. Hubbbert’s peak: the impending world oil shortage. Princeton, NJ: Springer Ntherlands, 2002. |
| [2] | Bardi U. Peak oil: the four stages of a new idea. Energy., 34 (2009) 323-6. |
| [3] | Sadorsky P. oil price shocks and stock market activity. Energy Economics., 34 (1999) 449-69. |
| [4] | Pareto VEIV, Pareto MP. The urban component of the energy crisis. SSRN, 2008. |
| [5] | Hoffmann W. PV solar electricity industry: market growth and perspective. Solar Energy Materials and Solar cells., 90 (2006) 3285-311. |
| [6] | A. Ibrahim, M. Y. Othman, M. H. Ruslan, S.Mat, K. Sopian, Recent advances in flat plate photovoltaic/ thermal (PV/T) solar collectors, Renewable and Sustainable Energy Reviews., 15 (2011) 352-365. |
| [7] | B. K. Koyunbaba, Z. Yilmaz, The comparison of trombe wall systems with single glass, double glass and PV panels, Renewable Energy., 45 (2012) 111-118. |
| [8] | [8] D. Kamthania, S. Nayak, G.N. Tiwari, Performance evaluation of a hybrid photovoltaic thermal double pass facade for space heating, Energy and Buildings., 43 (2011) 2274–2281. |
| [9] | GL. Jin, A. Ibrahim, YK. Chean, R. Daghigh, H. Ruslan, S. Mat, et al, Evaluation of single-pass photovoltaic-thermal air collector with rectangle tunnel absorber, A.J.of Applied Sciences., 7 (2010) 277-282. |
| [10] | T. T Chow, G. Pei, KF. Fong,Z.Lin, ALS. Chan, J.Ji, Energy and exergy analysis of photovoltaic-thermal collector with and without glass cover, Applied Energy., 86(3) (2009) 310-6. |
| [11] | S. Patankar, Numerical Heat Transfer and Fluid Flow, New York, 1980. |
| [12] | J.P.Van Doormaal, G.D. Raithby, Enhancements of the simple Method for predicting incompressible fluid flows, Numerical Heat Transfer., 7 (1984) 147-163. |
| [13] | R. Bennacer, Convection naturelle thermosolutale: simulation numérique des transferts et des structures d’écoulement, Doctoral thesis. University of Paris 6, France, 1993. |
| [14] | T.N. Anderson,M. Duke, G.L. Morrison, J.K. Carson, Performance of a building integrated photovoltaic/thermal (BIPVT) solar collector, Solar Energy., 83 (2009) 445-455. |
| [15] | I.Razvan. Caluianu, F. Baltaretu, Thermal modeling of a photovoltaic module under variable freeconvectionconditions, Applied Thermal Engineering., 33-34(2012)86-91. |


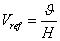 and
and 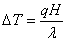 The dimensionless variables are:
The dimensionless variables are: 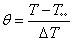 and
and 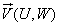 The dimensionless conservation equations of mass and momentum for the dimensionless natural convection flow of fluid are:v On the level of the fluid:
The dimensionless conservation equations of mass and momentum for the dimensionless natural convection flow of fluid are:v On the level of the fluid: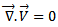
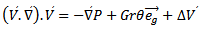
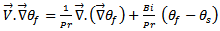
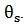 Thus, an energy equation should be written to determine
Thus, an energy equation should be written to determine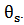 This equation reads:v On the level of the solid exchanger:
This equation reads:v On the level of the solid exchanger: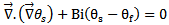
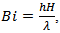 which takes the value zero away from interfaces.
which takes the value zero away from interfaces.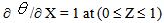 at X = A : W = 0, U = 0 and
at X = A : W = 0, U = 0 and 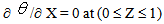 at Z = 1 :
at Z = 1 : 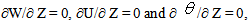 at the channel and W = 0, U = 0 and
at the channel and W = 0, U = 0 and 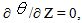 at the cavityat Z = 0 :
at the cavityat Z = 0 : 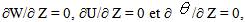 at the channel and W = 0, U = 0 and
at the channel and W = 0, U = 0 and 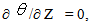 at the cavity
at the cavity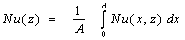 And the average Nusselt number,
And the average Nusselt number, 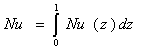 Where
Where 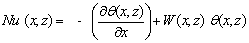 the local heat transfer at any point. Where W is the velocity component along Z axis.
the local heat transfer at any point. Where W is the velocity component along Z axis.









 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML