-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Materials Engineering
p-ISSN: 2166-5389 e-ISSN: 2166-5400
2013; 3(4): 87-91
doi:10.5923/j.ijme.20130304.04
Shear and Longitudinal Modulus of Elasticity in Structural Profiled Round Timber Beams
André L. Christoforo1, Felipe H. Icimoto2, Caio Victor Fernandes3, Juliano Fiorelli4, João Negrão5, Francisco A. Rocco Lahr6
1Department of Mechanical Engineering, Federal University of São João del-Rei, São João del-Rei, 36307-352, Brazil
2Department of Science and Engineering Materials, Engineering School of São Carlos (EESC/USP), São Carlos, 13566-590, Brazil
3Department of Forestry Engineering, Paulista State University (UNESP), Itapeva, 18409-010, Brazil
4Department of Biosystems Engineering, São Paulo State University (FZEA/USP), Pirassununga, 13635-900, Brazil
5Department of Structural Engineering, Coimbra University (UC), Coimbra, 74691070, Portugal
6Department of Structural Engineering, School of Engineering of São Carlos (EESC/USP), São Carlos, 13566-590, Brazil
Correspondence to: André L. Christoforo, Department of Mechanical Engineering, Federal University of São João del-Rei, São João del-Rei, 36307-352, Brazil.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
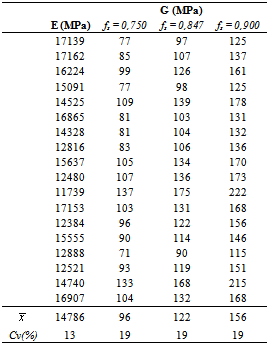
This research aimed to present, with the aid of the three-points static bending, conducted nondestructively, analytical methodology to determine the longitudinal (E) and the shear modulus (G) of elasticity in round timber beams. The wood used was Eucalyptus clones. Were used three different values to the form factor coefficient of the circular cross section, allowing evaluating the differences between the shear stiffness values obtained. The results of the analysis of variance indicated no statistical equivalence between the shear modulus of elasticity, revealing be significant the influence of the form factors used to determine the shear modulus of elasticity. The coefficient (λ) of the relationship between the modulus of elasticity (E=λ·G) obtained from the least squares method were equal to 118, revealing 5.9 higher than the relationship (E=20·G) presented in the Brazilian standard ABNT NBR 7190:1997. It is emphasized that these results may be different for the same or different wood species, justifying the use of this methodology in each research developed.
Keywords: Stiffness, Profiled Round Timber, Beams Theory
Cite this paper: André L. Christoforo, Felipe H. Icimoto, Caio Victor Fernandes, Juliano Fiorelli, João Negrão, Francisco A. Rocco Lahr, Shear and Longitudinal Modulus of Elasticity in Structural Profiled Round Timber Beams, International Journal of Materials Engineering , Vol. 3 No. 4, 2013, pp. 87-91. doi: 10.5923/j.ijme.20130304.04.
1. Introduction
- The shear modulus of elasticity of timber pieces, as well as other materials, presents as a fundamental structural variable especially in designs involving short beams and parts subject to the action of the torsion[1-3].For the design of various structures in wood, such as silos, roofs, buildings, bridges, among others, engineers, architects and designers make use of normative documents, such as the Brazilian standard ABNT NBR 7190:1997 (Design of Structures Wood), which does not address the anisotropy of wood, with an empirical relationship for obtaining the shear modulus of elasticity (G) known longitudinal modulus of elasticity (E) expressed as: G=E/20, which motivates development of new research on this topic, and highlight the work done by Rocco Lahr[4], Burdzik Nkwera[5],Zangiácomo Rocco Lahr[6] and Christoforo et al.[7].Rocco Lahr[4] study, among others, the influence of the dimensions of the test pieces of lumber for which the effect of shear forces become negligible in the calculation of displacements, reaching the ratio L/h≥21, where L is the useful length and h is the height of the cross section of the specimen.Burdzik and Nkwera[5] evaluated the shear and the longitudinal modulus of elasticity in Eucalyptus grandis wooden beams by the transverse vibration wave. The results demonstrate that the proposed method is employable for determining the modulus of elasticity, showing consistency in results when compared with the properties of wood coming from normative document.Zangiácomo and Rocco Lahr[6] studied the relationship between the length and diameter (D) in round timber beams for which the effect of shear forces becomes negligible in the calculation of displacements, arriving at 24 and 15 relations for the Pinus elliottii and Pinus caribaea wood species, respectively.Christoforo et al.[7] presented an analytical methodology for the calculation of the shear and longitudinal modulus of elasticity in pieces of lumber, using the three-points static bending, adapted from the Brazilian standard ABNT NBR 7190[8], based on the methodology presented by Rocco Lahr[4]. The wood used in the tests were Pinus elliottii and Corymbia citriodora. Equations for the calculation of the elastic moduli were developed according to the method of virtual forces, and the shape of the shear coefficient for rectangular cross section was adopted as 1.20. Results of the coefficients (α) between the modules of elasticity (E=α·G) for the Pinus elliottii and Corymbia citriodora wood species were respectively equal to 18.70 and 21.20, and very close to the coefficient (20) established by the Brazilian standard ABNT NBR 7190[8].In order to contribute to better understanding of the properties of shear stiffness, this research, based on work carried out by Christoforo et al.[7], aimed to present, with the aid of the three-points static bending and the Timoshenko beams theory, an analytical methodology for obtaining the shear and longitudinal modulus of elasticity in profiled round timber beams with structural dimensions, investigating the influence of the form factor in the calculation of the shear modulus of elasticity.
2. Material and Methods
- The experimental methodology developed to calculate the modulus of elasticity E and G in structural round timber was based on research developed by Rocco Lahr[4], as also done in the work of Christoforo et al.[7]. The moduli of elasticity were obtained in the condition of geometric linearity, the largest displacements being limited to the experiments L/200 reason, as defined by the small displacements of Brazilian standard ABNT NBR 7190[8].The Virtual Force Method (VSM) was employed on the structural model of the three-point static bending (Figure 1) in order to obtain the expression for the calculation of the displacement (δ) at the midpoint of the element, considering the bending moment and shear efforts.
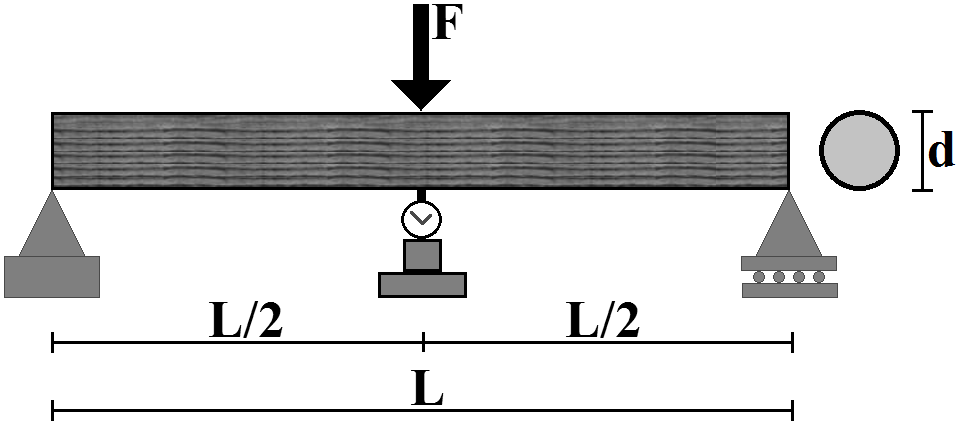 | Figure 1. Three-point static bending model |
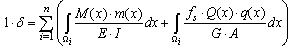 | (1) |
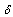 - linear displacement or rotation to be calculated by the use of force or virtual moment virtual with module 1;M(x) - variation of the bending moment for a section of the structure according to the actual load history;m(x) - variation of the bending moment for a section of the structure according to the employment of a unit force or moment applied at one point of interest;Q(x) - variation of shear for a slice of the structure according to the actual load history;q(x) - variation of shear for a slice of the structure according to the employment of a unit force or moment applied at one point of interest;fs - form factor of the cross section (depending on the geometry of the cross sections);Ω - integration domain;E - longitudinal modulus of elasticity or Young's modulus;I - moment of inertia of the cross section;G - shear modulus of elasticity;A - cross-sectional area;L - length of the beam.Using Equation 1 adapted for the structural model of the three-point bending (Figure 1), the displacement at the midpoint is expressed by Equation 2.
- linear displacement or rotation to be calculated by the use of force or virtual moment virtual with module 1;M(x) - variation of the bending moment for a section of the structure according to the actual load history;m(x) - variation of the bending moment for a section of the structure according to the employment of a unit force or moment applied at one point of interest;Q(x) - variation of shear for a slice of the structure according to the actual load history;q(x) - variation of shear for a slice of the structure according to the employment of a unit force or moment applied at one point of interest;fs - form factor of the cross section (depending on the geometry of the cross sections);Ω - integration domain;E - longitudinal modulus of elasticity or Young's modulus;I - moment of inertia of the cross section;G - shear modulus of elasticity;A - cross-sectional area;L - length of the beam.Using Equation 1 adapted for the structural model of the three-point bending (Figure 1), the displacement at the midpoint is expressed by Equation 2.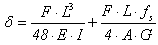 | (2) |
 | Figure 2. Bending test in the profile round timber parts: first (a) and the second test (b) |
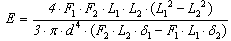 | (3) |
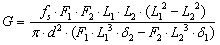 | (4) |
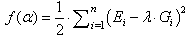 | (5) |
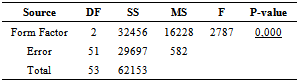
3. Results
- Table 1 shows the results of the two modulus of elasticity, is the sample mean and Cv the variation coefficient.
|
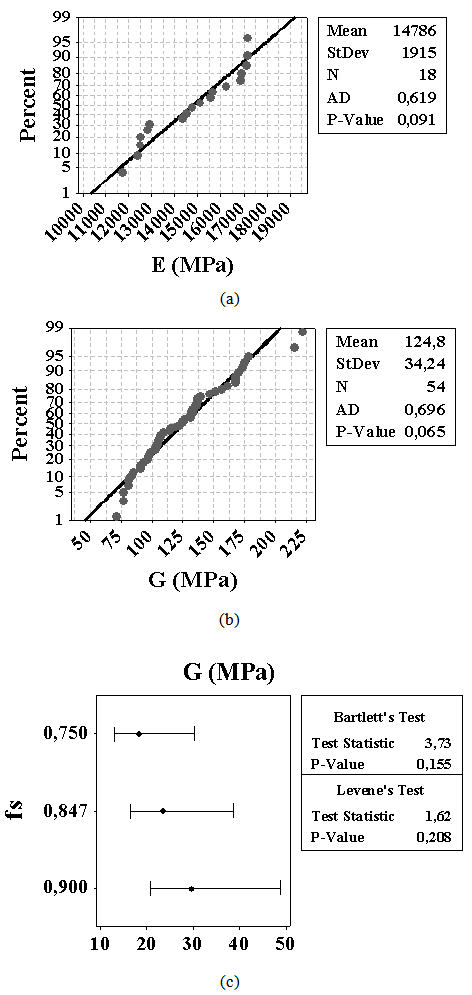 | Figure 3. Results of normality test (a, b) and homogeneity of variances (c) |
|
|
4. Conclusions
- The results of the shear modulus of elasticity for the wood investigated were found to be dependent on the choice of the form coefficients of circular cross-section, providing the shape coefficient of 0.90 the highest values.The average value of the coefficients of the relationship between the modulus of elasticity of the Eucalyptus wood was significantly higher than the value set by the Brazilian standard, providing values of shear modules less when compared to the shear modulus of this standard.The sensitivity of the method, the results obtained here should not be extrapolated to woods with the same or different species, thereby justifying the use of this calculation method developed in each study and other relations between length and diameter of the elements different from those here evaluated.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML