Sergejus Rimovskis, Arturas Sabaliauskas
Department of Mechanical Engineering, Siauliai University, Siauliai, LT-76353, Lithuania
Correspondence to: Sergejus Rimovskis, Department of Mechanical Engineering, Siauliai University, Siauliai, LT-76353, Lithuania.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
Engineering theory of elastic plastic bending is used in solving a grate variety of strength and durability problems. The accuracy of analysis depends on stress-strain curve idealization model. The elastic linear hardening stress-strain relation is simple and frequently used. But the actual stress-strain behaviour of ductile material in plastic region is non-linear and, therefore, elastic power hardening material model is more preferable. Moreover, the properties of monotonic tension and compression as proportional limits and parameters of hardening can differ. In this regard, analytical solution for rectangular and circular cross-section elements loading by monotonic elastic plastic pure bending is presented in the paper. The simple power relation of stress and strain response is used. The equations describing deviation of the stress neutral axis from centroidal axis of an element and dimensionless bending moment are derived.Mechanical properties of majority of ductile materials determined by tensile and compressive testing usually differ. Consequently constants of idealized stress-strain curves (proportional limits and parameters of hardening) are also different. Analysis of pure bending of rectangular and circular cross-section element can be realized with regard to this. The values of dimensionless bending moment can be found directly from presented diagrams or calculated by deduced formulas.
Keywords:
Pure Bending, Elastic Plastic, Power Hardening
Cite this paper:
Sergejus Rimovskis, Arturas Sabaliauskas, "Analysis of Rectangular and Circular Cross-section Power Hardening Elements Under Pure Bending", International Journal of Materials Engineering, Vol. 2 No. 6, 2012, pp. 84-89. doi: 10.5923/j.ijme.20120206.03.
1. Introduction
The study of elastic-plastic bending has a wide field of application. Engineering and mathematical theories of plastic bending are well studied in T. X. Yu at al. book[1]. The authors include many experimental verifications as well as theoretical results. Elastic-plastic analysis of beam-like structures of different cross-sections under bending is considered in[2-10]. The authors employ different models of non-linear stress-strain idealization. The most used models are linear and power hardening. M. Daunys performed theoretical analysis of rectangular cross-section linear hardening beam subjected to static and cyclic pure bending[11]. The author analyses the drift of the stress neutral axis from the centroidal axis of beam, if parameters of plastic tension and compression (proportional limits, modulus of hardening) are not equal. Circular cross-section linear hardening element under pure bending is studied in[12, 13]. Derived equations are fitted to analysis of cyclic pure bending.Power hardening stress-strain curve model is more preferable in analytical researches of strength of structures than linear hardening one because of better accuracy. Therefore, using of such a kind of idealization in pure bending analysis has not only theoretical but practical importance and applications as well.
2. Pure Bending of Rectangular Cross-Section Element
It is assumed that in case of pure bending a transverse plane section perpendicular to the centroidal axis of the beam before deformation remains plane after deformation and that a cross-section is perpendicular to the centroidal axis after bending. It is also assumed that normal stresses and strains in the transverse and lateral directions are neglected and every fiber of the beam is either under uniaxial tension or under uniaxial compression. Therefore stress and strain distribution in the longitudinal cross-section of an element fit the schemes presented in Figs 1 and 2.Stress 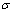 and strain
and strain 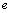 of longitudinal fibers are expressed in dimensionless units
of longitudinal fibers are expressed in dimensionless units 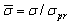 and
and 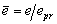 , where
, where 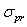 and
and 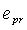 are the values corresponding to proportional limit. Monotonic stress-strain characteristics (tension or compression) with lower rate of proportional limit are marked by index 1. Therefore,
are the values corresponding to proportional limit. Monotonic stress-strain characteristics (tension or compression) with lower rate of proportional limit are marked by index 1. Therefore, 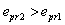 and
and 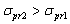 . Modulus of elasticity
. Modulus of elasticity 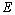 is the same for both cases. According to the law of equilibrium, we obtain
is the same for both cases. According to the law of equilibrium, we obtain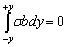 | (1) |
and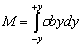 | (2) |
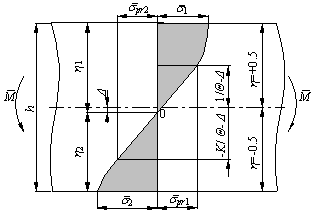 | Figure 1. Stress distribution in the longitudinal cross-section of an element |
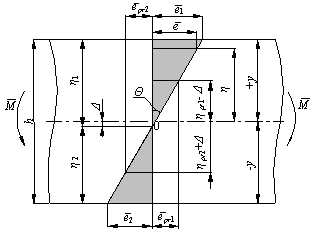 | Figure 2. Strain distribution in the longitudinal cross-section of an element |
According to Fig. 2, 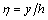 . Hence, dimensional expression of distant
. Hence, dimensional expression of distant 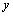 is
is 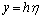 and
and 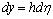 . Substituting
. Substituting 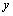 and
and 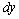 in Eq. (1) we get
in Eq. (1) we get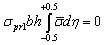 | (3) |
It is evident that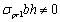 and so Eq. (3) can be simplified to
and so Eq. (3) can be simplified to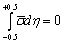 | (4) |
In the plastically deformed fibers on the convex side of the beam, as in case of the monotonic tension, stress-strain curve with proportional limit 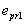 is used, so
is used, so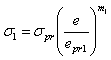 | (5) |
In the fibers on the concave side of the beam with proportional limit 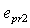 we get
we get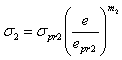 | (6) |
In Eq. (5) and (6) 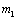 and
and 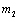 are strain hardening exponents. After dividing Eqs. (5) and (6) by
are strain hardening exponents. After dividing Eqs. (5) and (6) by 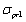 and rearranging, we obtain dimensionless stress expressions
and rearranging, we obtain dimensionless stress expressions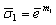 | (7) |
and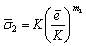 | (8) |
In Eq. (8), 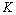 is a coefficient accounting for difference of proportional limits
is a coefficient accounting for difference of proportional limits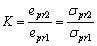 | (9) |
If 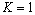 and
and 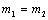 , the position of the neutral axis coincides with the cross-section centroidal axis. If
, the position of the neutral axis coincides with the cross-section centroidal axis. If  and (or)
and (or) 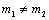 , the position of the neutral axis deviates from centroidal axis of an element by value
, the position of the neutral axis deviates from centroidal axis of an element by value  . We mark the strain of fiber of centroidal axis as
. We mark the strain of fiber of centroidal axis as 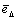 and transform Eqs. (7) and (8) to
and transform Eqs. (7) and (8) to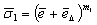 | (10) |
and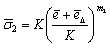 | (11) |
It is evident, that if 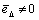 , the strains on the convex and concave sides of an element are not equal (
, the strains on the convex and concave sides of an element are not equal (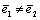 ). According to Fig. 1,
). According to Fig. 1, 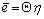 and
and 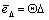 , where
, where 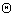 is the dimensionless angle of cross-sections deflection. In regard to this, final expressions of plastic stress are
is the dimensionless angle of cross-sections deflection. In regard to this, final expressions of plastic stress are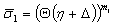 | (12) |
and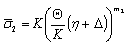 | (13) |
In the fibers deformed elastically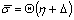 | (14) |
Hence, integral (4) can be written as a sum of three integrals representing three different regions of strains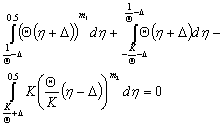 | (15) |
In case of pure bending, if 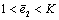 (the fibers on the convex side of an element exceeded
(the fibers on the convex side of an element exceeded 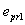 and the fibers on the concave side of an element are still under elastic conditions), Eq. (14) can by simplified
and the fibers on the concave side of an element are still under elastic conditions), Eq. (14) can by simplified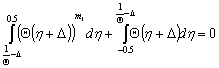 | (16) |
Dimensionless distant from extreme fiber with 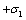 to the neutral axis is
to the neutral axis is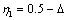 | (17) |
By referring to integrals (15), (16) and Eq. (17), distant 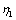 is found for the angle
is found for the angle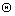 . Subsequently the strains
. Subsequently the strains 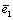 and
and 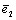 can be obtained.The integral (2) can be transformed considering that
can be obtained.The integral (2) can be transformed considering that 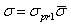 ,
, 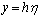 and
and 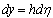
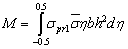 | (18) |
or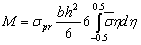 | (19) |
The pure bending moment corresponding to the proportional limit stress is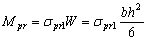 | (20) |
So, the integral (19) can be written in dimensionless form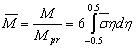 | (21) |
Substituting 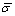 (Eqs. (12)-(14)) in (21) we get:
(Eqs. (12)-(14)) in (21) we get: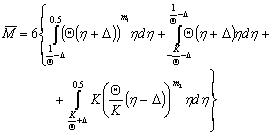 | (22) |
In case, if 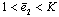
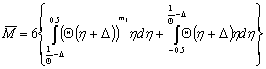 | (23) |
Integrals (21) and (22) allow to determine moment  depending on maximum strain. Analytical expressions of integrals (15), (16), (22) and (23) exist, but are not presented.Figs. 3 and 4 represent curves of functions
depending on maximum strain. Analytical expressions of integrals (15), (16), (22) and (23) exist, but are not presented.Figs. 3 and 4 represent curves of functions  and
and  in the strain range
in the strain range 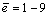 for the fallowing values of parameters
for the fallowing values of parameters 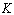 and
and 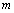 :
: 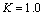 ;
; 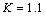 ;
; 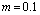 ;
; 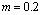 ;
; 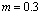 ;
; 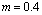 .
.
3. Pure Bending of Circular Cross-Section Element
 | Figure 3. The distance from extreme fiber with 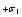 to the neutral axis of rectangular cross-section element vs. monotonic tension strain, for to the neutral axis of rectangular cross-section element vs. monotonic tension strain, for  (a) and (a) and 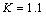 (b) (b) |
In case of elastic plastic pure bending of circular cross-section beam, the stress and strain distribution in the longitudinal cross-section also fit the schemes presented in Figs. 1 and 2. But in the transversal cross-section some differences are seen (see Fig. 5).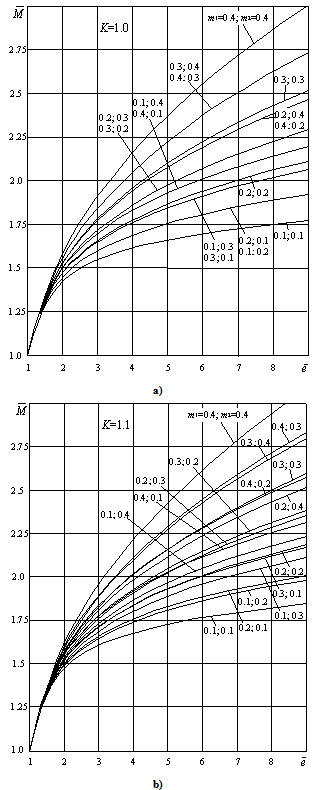 | Figure 4. Dimensionless bending moment of rectangular cross-section element vs. monotonic tension strain, for 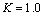 (a) and (a) and 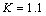 (b) (b) |
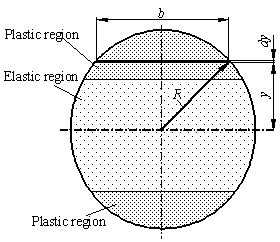 | Figure 5. The regions of elastic and plastic strains in the transversal cross-section of a circular element |
The width of circular cross-section element 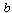 depends on distance
depends on distance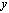 . Considering, that
. Considering, that 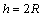 and
and 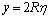 we get
we get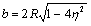 | (24) |
It is evident, that 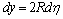 , so integral (1) can be expressed as
, so integral (1) can be expressed as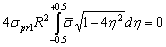 | (25) |
and simplified to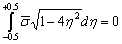 | (26) |
Using 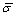 defined by Eqs. (12)-(14), allows to transform integral (26)
defined by Eqs. (12)-(14), allows to transform integral (26)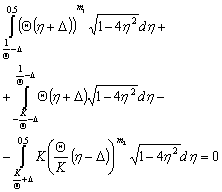 | (27) |
And in case, if 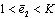
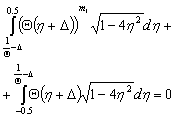 | (28) |
Next we transform the integral (2) to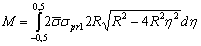 | (29) |
and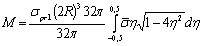 | (30) |
In case of pure bending of circular cross-section element, the bending moment corresponding to the proportional limit is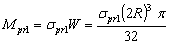 | (31) |
Hence, dimensionless bending moment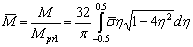 | (32) |
The final expression of 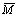 is
is 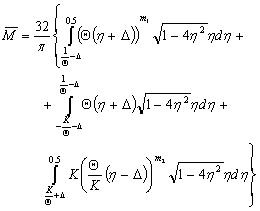 | (33) |
In case, if 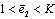
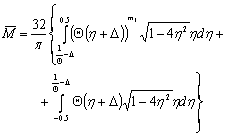 | (34) |
Analytical expressions of integrals (27), (28), (33) and (34) do not exist. These integrals can be solved numerically.Theoretical 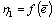 and
and  curves for the same values of
curves for the same values of  and
and 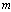 are presented in Figs. 6 and 7.The developed analytical solution of monotonic elastic plastic pure bending can be used to analyse the cyclic elastic plastic pure bending as it is presented by formulas[11, 12].
are presented in Figs. 6 and 7.The developed analytical solution of monotonic elastic plastic pure bending can be used to analyse the cyclic elastic plastic pure bending as it is presented by formulas[11, 12].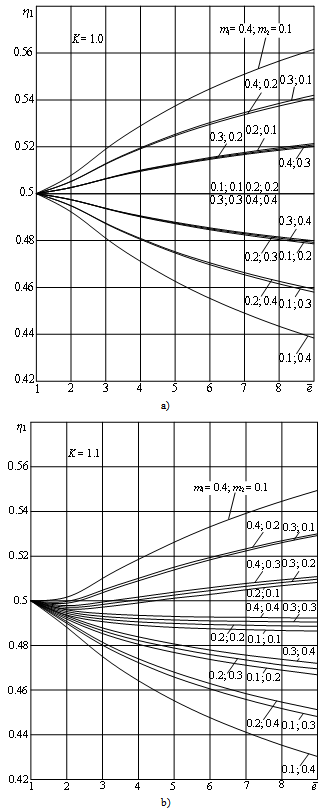 | Figure 6. The distance from extreme fiber with 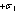 to the neutral axis of circular cross-section element vs. monotonic tension strain, for to the neutral axis of circular cross-section element vs. monotonic tension strain, for 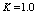 (a) and (a) and 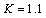 (b) (b) |
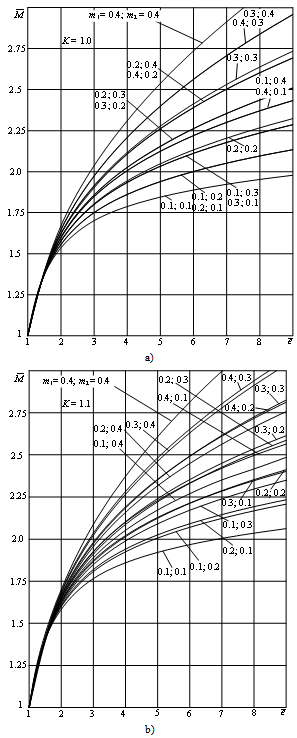 | Figure 7. Dimensionless bending moment of circular cross-section element vs. monotonic tension strain, for 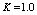 (a) and (a) and 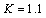 (b) (b) |
4. Conclusions
Elastic-power hardening idealization of uniaxial stress strain curve is used in theoretical research of rectangular and circular cross-section element under elastic plastic pure bending. Presented derivations allow to calculate deviation of stress neutral axis from centroidal axis of an element and pure bending moment versus monotonic strain if parameters of plastic tension and compression (proportional limits, exponents of hardening) are not equal. Derived expressions of bending moment can be used in theoretical research of cyclic elastic plastic pure bending.
References
| [1] | Yu T. X., Zhang L. C. Plastic Bending: Theory and Applications. Series on Engineering Mechanics, vol. 2, World Scientific. 572 pp. 1996. |
| [2] | Štok B., Halilovič M.. Analytical Tracing of the Evolution of the Elasto-Plastic State during the Bending of Beams with a Rectangular Cross-Section. Journal of Mechanical Engineering, vol. 53, p. 806-818. 2007. |
| [3] | Štok B., Halilovič M. Analytical Solutions in Elasto-Plastic Bending of Beams with Rectangular Cross-Section. Applied Mathematical Modeling, vol. 33, p. 1749-1760. 2009. |
| [4] | Rees D. W. Descriptions of Reversed Yielding in Bending. Journal of Mechanical Engineering Science, vol. 221, p. 981-991. 2007. |
| [5] | Bin J., Wanji C. A New Analytical Solution of Pure Bending Beam in Couple Stress Elasto-Plasticity: Theory and Applications. International Journal of Solids and Structures, vol. 47, p. 779-785. 2010. |
| [6] | Eraslan A. N., Arslan E. A Concise Analytical Treatment of Elastic-Plastic Bending of a Strain Hardening Curved Beam. Journal of Applied Mathematics and Mechanics, vol. 88, p. 600-616. 2008. |
| [7] | Arslan E., Eraslan A. N. Analytical solution to the bending of a nonlinearly hardening wide curved bar. Acta Mechanica, vol. 210, p. 71-84. 2010 |
| [8] | Yang J., Reid S. R. Approximate estimation of Hardening-Softening Behaviour of Circular Pipes Subjected to Pure Bending. Acta Mechanica Sinica, vol. 13, p. 227-240. 1997. |
| [9] | Lanzagorta J. L., Meizoso A. M. 3-Point Bending of Bars and Rods Made of Materials Obeying a Ramberg-Osgood Criterion. World Journal of Mechanins, vol. 1, p. 71-77. 2011. |
| [10] | Chakrabarty J., Lee W.B., Chan K.C. An Analysis of the Plane-Strain Bending of an Orthotropic Sheet in the Elastic/Plastic range. Journal of Materials Processing Technology, vol. 104, p. 48-52. 2000. |
| [11] | Daunys M. Solution for Rectangular Cross-Section Bars above Proportionality Stress. Electrotechnics and Mechanics. p. 61-69. 1969 (in Lithuanian). |
| [12] | Daunys M., Rimovskis S. Analysis of Circular Cross-Section Bar, Loaded by Static and Cyclic Elasto-Plastic Pure Bending. Mechanika, vol. 33, p. 5-10. 2002. |
| [13] | Daunys M., Rimovskis S. Analysis of Circular Cross-Section Element, Loaded by Static and Cyclic Elastic–Plastic Pure Bending. International Journal of Fatigue, vol. 28, p. 211-222. 2006. |

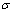 and strain
and strain 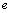 of longitudinal fibers are expressed in dimensionless units
of longitudinal fibers are expressed in dimensionless units 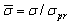 and
and 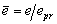 , where
, where 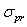 and
and 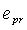 are the values corresponding to proportional limit. Monotonic stress-strain characteristics (tension or compression) with lower rate of proportional limit are marked by index 1. Therefore,
are the values corresponding to proportional limit. Monotonic stress-strain characteristics (tension or compression) with lower rate of proportional limit are marked by index 1. Therefore, 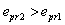 and
and 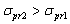 . Modulus of elasticity
. Modulus of elasticity 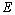 is the same for both cases. According to the law of equilibrium, we obtain
is the same for both cases. According to the law of equilibrium, we obtain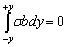
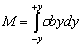


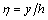 . Hence, dimensional expression of distant
. Hence, dimensional expression of distant 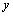 is
is 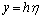 and
and 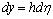 . Substituting
. Substituting 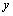 and
and 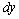 in Eq. (1) we get
in Eq. (1) we get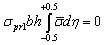
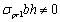 and so Eq. (3) can be simplified to
and so Eq. (3) can be simplified to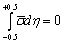
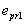 is used, so
is used, so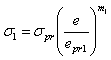
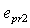 we get
we get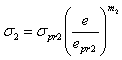
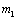 and
and 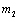 are strain hardening exponents. After dividing Eqs. (5) and (6) by
are strain hardening exponents. After dividing Eqs. (5) and (6) by 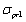 and rearranging, we obtain dimensionless stress expressions
and rearranging, we obtain dimensionless stress expressions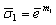
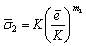
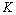 is a coefficient accounting for difference of proportional limits
is a coefficient accounting for difference of proportional limits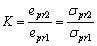
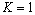 and
and 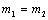 , the position of the neutral axis coincides with the cross-section centroidal axis. If
, the position of the neutral axis coincides with the cross-section centroidal axis. If 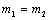 and (or)
and (or) 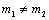 , the position of the neutral axis deviates from centroidal axis of an element by value
, the position of the neutral axis deviates from centroidal axis of an element by value  . We mark the strain of fiber of centroidal axis as
. We mark the strain of fiber of centroidal axis as 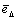 and transform Eqs. (7) and (8) to
and transform Eqs. (7) and (8) to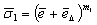
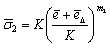
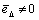 , the strains on the convex and concave sides of an element are not equal (
, the strains on the convex and concave sides of an element are not equal (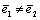 ). According to Fig. 1,
). According to Fig. 1, 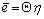 and
and 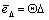 , where
, where 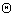 is the dimensionless angle of cross-sections deflection. In regard to this, final expressions of plastic stress are
is the dimensionless angle of cross-sections deflection. In regard to this, final expressions of plastic stress are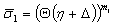
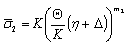
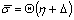
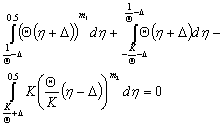
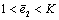 (the fibers on the convex side of an element exceeded
(the fibers on the convex side of an element exceeded 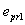 and the fibers on the concave side of an element are still under elastic conditions), Eq. (14) can by simplified
and the fibers on the concave side of an element are still under elastic conditions), Eq. (14) can by simplified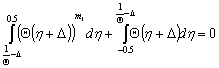
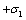 to the neutral axis is
to the neutral axis is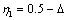
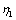 is found for the angle
is found for the angle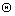 . Subsequently the strains
. Subsequently the strains 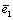 and
and 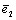 can be obtained.The integral (2) can be transformed considering that
can be obtained.The integral (2) can be transformed considering that 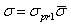 ,
, 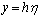 and
and 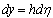
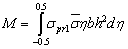
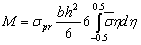
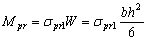
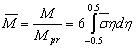
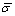 (Eqs. (12)-(14)) in (21) we get:
(Eqs. (12)-(14)) in (21) we get: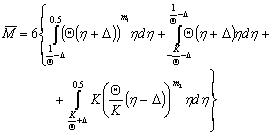
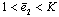
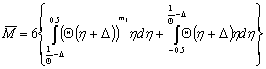
 depending on maximum strain. Analytical expressions of integrals (15), (16), (22) and (23) exist, but are not presented.Figs. 3 and 4 represent curves of functions
depending on maximum strain. Analytical expressions of integrals (15), (16), (22) and (23) exist, but are not presented.Figs. 3 and 4 represent curves of functions 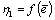 and
and 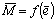 in the strain range
in the strain range 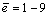 for the fallowing values of parameters
for the fallowing values of parameters 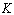 and
and 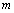 :
: 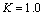 ;
; 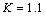 ;
; 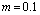 ;
; 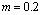 ;
; 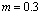 ;
; 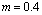 .
.
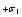 to the neutral axis of rectangular cross-section element vs. monotonic tension strain, for
to the neutral axis of rectangular cross-section element vs. monotonic tension strain, for 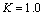 (a) and
(a) and 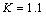 (b)
(b)
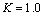 (a) and
(a) and 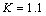 (b)
(b)
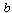 depends on distance
depends on distance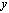 . Considering, that
. Considering, that 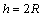 and
and 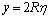 we get
we get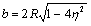
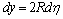 , so integral (1) can be expressed as
, so integral (1) can be expressed as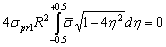
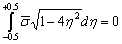
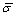 defined by Eqs. (12)-(14), allows to transform integral (26)
defined by Eqs. (12)-(14), allows to transform integral (26)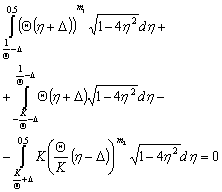
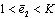
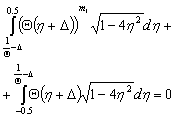
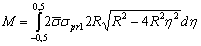
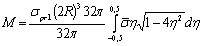
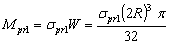
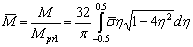
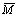 is
is 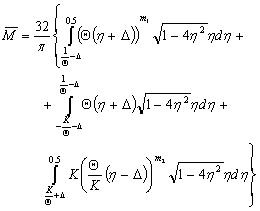
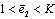
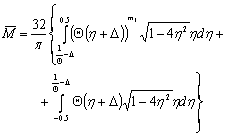
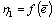 and
and 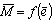 curves for the same values of
curves for the same values of 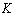 and
and 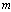 are presented in Figs. 6 and 7.The developed analytical solution of monotonic elastic plastic pure bending can be used to analyse the cyclic elastic plastic pure bending as it is presented by formulas[11, 12].
are presented in Figs. 6 and 7.The developed analytical solution of monotonic elastic plastic pure bending can be used to analyse the cyclic elastic plastic pure bending as it is presented by formulas[11, 12].
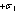 to the neutral axis of circular cross-section element vs. monotonic tension strain, for
to the neutral axis of circular cross-section element vs. monotonic tension strain, for 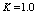 (a) and
(a) and 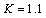 (b)
(b)
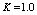 (a) and
(a) and 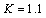 (b)
(b) Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML