-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Materials and Chemistry
p-ISSN: 2166-5346 e-ISSN: 2166-5354
2022; 12(2): 27-31
doi:10.5923/j.ijmc.20221202.02
Received: Aug. 12, 2022; Accepted: Aug. 26, 2022; Published: Sep. 15, 2022

Investigation of the Conversion Process of Calcium and Magnesium Chloride Solution with Sodium Chloride
Dilmurod A. Ergashev, Shokhida Sh. Khamdamova
Department of Chemistry and Chemical Technology, Fergana Polytechnic Institute, Fergana, Republic of Uzbekistan
Copyright © 2022 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

The process of conversion of 37.14% of solutions of calcium and magnesium chlorides with sodium chlorate at 50, 75, and 90°C with the evaporation of conversion solutions was studied. The activation energies of the process and the order and rate constant of the conversion reaction were determined depending on the temperature, time and conditions of the processes. The order of the process of conversion of calcium and magnesium chlorides with sodium chlorate is equal to one. This is confirmed by the fact that the conversion rate constant, calculated from experimental data, remains almost constant for each temperature. Straight Line Dependency 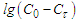 from
from 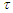 also indicates the first order of the process of conversion of calcium and magnesium chlorides with sodium chlorate. The conversion rate constant increases with increasing temperature. Its temperature dependence obeys the Arrhenius law. To establish the values of the conversion rate constant for different temperatures, the constants
also indicates the first order of the process of conversion of calcium and magnesium chlorides with sodium chlorate. The conversion rate constant increases with increasing temperature. Its temperature dependence obeys the Arrhenius law. To establish the values of the conversion rate constant for different temperatures, the constants 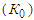 for 37.14% solutions of calcium chloride by the Arrhenius equation and the equation for the dependence of lgK on 1/T were derived. This is confirmed by the linear graphical dependence of lgK on 1/T. The expediency of carrying out the conversion process with evaporation at a temperature of 100°C.
for 37.14% solutions of calcium chloride by the Arrhenius equation and the equation for the dependence of lgK on 1/T were derived. This is confirmed by the linear graphical dependence of lgK on 1/T. The expediency of carrying out the conversion process with evaporation at a temperature of 100°C.
Keywords: Conversion, Evaporation, Degree of conversion, Activation energy, Rate constant
Cite this paper: Dilmurod A. Ergashev, Shokhida Sh. Khamdamova, Investigation of the Conversion Process of Calcium and Magnesium Chloride Solution with Sodium Chloride, International Journal of Materials and Chemistry, Vol. 12 No. 2, 2022, pp. 27-31. doi: 10.5923/j.ijmc.20221202.02.
Article Outline
1. Introduction
- In the world, the main factor in the quality and high yield of agricultural plants is the rational use of mineral fertilizers, stimulants and pesticides. Therefore, much attention has recently been paid to the development of new, highly effective, safe types of defoliants for cotton, which effectively accelerates the processes of deleafing, the opening of mature bolls, increasing the pre-frost harvest of the first varieties, and preventing the mass reproduction of autumn generations of cotton sucking pests.Currently, preparations for the protection of agricultural crops, defoliants and plant growth regulators are mainly imported from abroad in the form of active principles and preparative forms. For the production of magnesium chlorate defoliant (which contains 36% of the active substance in its composition) [1] at Ferganaazot JSC, the initial raw material source of bischofite (magnesium chloride) is imported from Volgograd (Russia) or Turkmenistan for foreign currency. This leads to an increase in the cost of the defoliant.To solve this problem, employees of the Institute of General Chemistry of the Academy of Sciences of the Republic of Uzbekistan and FerPI developed a technology for obtaining a new calcium-magnesium chlorate defoliant by using it as raw material, instead of imported "bischofite", products of hydrochloric acid decomposition of dolomites m.r. "Shorsu" and "Pachkamar" [2].The purpose of this work is to develop a technology for obtaining new defoliants of complex action, having defoliating activity, accelerating the maturation and opening of capsules based on calcium-magnesium chlorate preparation obtained from dolomites of the Navbakhor deposit [3,4,5,6,7,8].
2. Materials and Methods
- To issue practical recommendations for the preparation of calcium and magnesium chlorates, the process of conversion of calcium and magnesium chlorides with sodium chlorate was studied depending on temperature and time duration. The study was carried out at temperatures of 50, 75, and 90°C and the duration of experiments was 30, 60, 90, and 120 minutes with the evaporation of conversion solutions. A 500 cm3 round-bottom flask equipped with a stirrer was charged with 200 g of a 37% aqueous solution of calcium and magnesium chlorides obtained by hydrochloric acid decomposition of dolomites and an equivalent amount of sodium chlorate. A solution of calcium and magnesium chlorides was obtained by decomposition of local dolomites (the composition is given in Table 1.) with a 32% hydrochloric acid solution, as a result of which a solution containing37.0% of the sum of calcium and magnesium chlorides, its density is 1.32÷1.35 g/cm3, pH 5.0÷5.5. Next, the flask was placed in a thermostat with a set temperature (50, 75, 90°C) and intensively mixed. Accordingly, after 30, 60, 90, and 120 minutes, the liquid phase was separated from the sediment and the corresponding chemical analysis of both phases was carried out.
 | Table 1. Chemical composition of the dolomite sample (wt.%) |
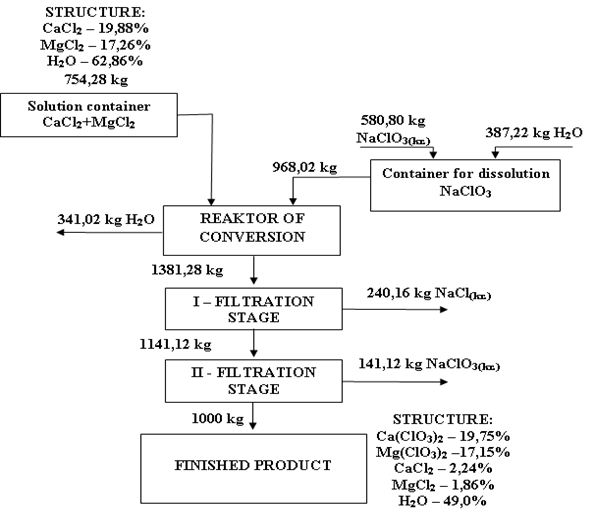 | Figure 1. The material balance of obtaining 1 ton of calcium and magnesium chlorides |
3. Results and Discussions
- Based on the data obtained, the degree of conversion of calcium-magnesium chloride with sodium chlorate and the consumption of initial components during the conversion was established (Table 2, Fig. 2).Table 2 and Fig. 2 show that the degree of conversion significantly depends on temperature and increases with its growth. For processes of 37.14% solutions of calcium and magnesium chlorides to chlorates within 60 minutes, the degree of conversion at 323, 348, and 363 °K is 11.89; 22.36; 30.68% respectively. After 90 minutes, the degree of conversion reaches 17.66; 30.89; 38.94%, respectively, for 37.14% solutions of calcium and magnesium chloride, at temperatures of 323; 348 and 363 °K.
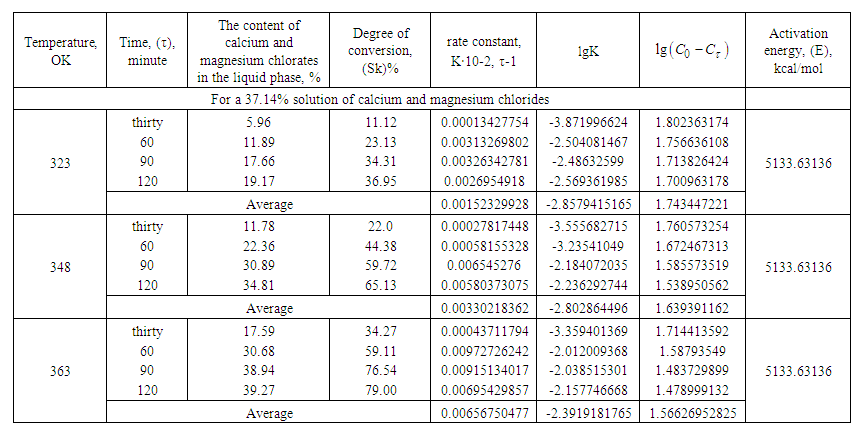 | Table 2. Dependence of the rate constant and the degree of conversion on the temperature and duration of the process in the conversion of calcium chloride solutions from evaporation |
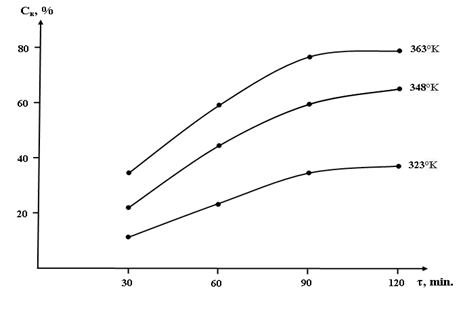 | Figure 2. Dependence of the degree of conversion of calcium and magnesium chloride with sodium chlorate on the temperature and duration of the process with the evaporation of conversion solutions |
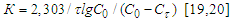 | (1) |
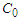 and
and 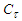 are the concentrations of calcium and magnesium chlorides (or sodium chlorate), respectively, at the initial stage of conversion and over the elapsed time interval (τ), K is the conversion rate constant.According to the obtained data, the order of the conversion reaction of calcium and magnesium chlorides with sodium chlorate is equal to one. This is confirmed by the fact that the conversion rate constant calculated by equation (2) based on experimental data remains practically constant for each temperature (Table 2). In addition, the linear dependence
are the concentrations of calcium and magnesium chlorides (or sodium chlorate), respectively, at the initial stage of conversion and over the elapsed time interval (τ), K is the conversion rate constant.According to the obtained data, the order of the conversion reaction of calcium and magnesium chlorides with sodium chlorate is equal to one. This is confirmed by the fact that the conversion rate constant calculated by equation (2) based on experimental data remains practically constant for each temperature (Table 2). In addition, the linear dependence 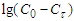 on
on 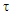 also indicates the first order of the process of conversion of calcium and magnesium chlorides with sodium chlorate (Fig. 3). The conversion rate constant increases with increasing temperature (Table 2). Its dependence on temperature obeys the Arrhenius law. This is confirmed by the rectilinear graphical dependence of lgK on 1/T.
also indicates the first order of the process of conversion of calcium and magnesium chlorides with sodium chlorate (Fig. 3). The conversion rate constant increases with increasing temperature (Table 2). Its dependence on temperature obeys the Arrhenius law. This is confirmed by the rectilinear graphical dependence of lgK on 1/T. 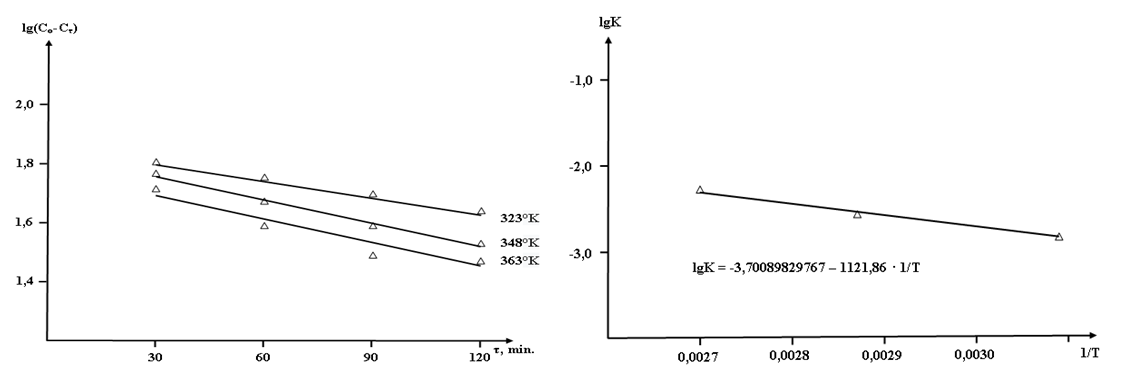 | Figure 3. Dependence of 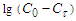 on τ for conversion processes of 37.14% solutions of calcium and magnesium chlorides with sodium chlorate, as well as the dependence of lgK on 1/T on τ for conversion processes of 37.14% solutions of calcium and magnesium chlorides with sodium chlorate, as well as the dependence of lgK on 1/T |
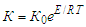 | (2) |
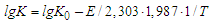 | (3) |
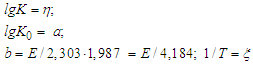 | (4) |
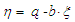 | (5) |
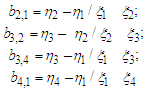 and by calculating the individual values of "b" based on experimental data, we find the average value of "b".The calculation of the average value "a" is found by the formula:
and by calculating the individual values of "b" based on experimental data, we find the average value of "b".The calculation of the average value "a" is found by the formula: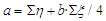 | (6) |
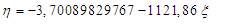 | (7) |
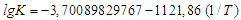 | (8) |
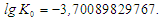 From here or
From here or 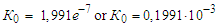 After substituting the values of K0 and E, the empirical Arrhenius equation (3) takes the form
After substituting the values of K0 and E, the empirical Arrhenius equation (3) takes the form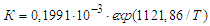 | (9) |
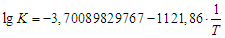 | (10) |
4. Conclusions
- Thus, from the results of the studies it follows that to obtain a defoliant with an optimal content of the active substance, it is recommended to carry out the conversion of 37.14% solutions of calcium and magnesium chloride with sodium chlorate at a molar ratio of components 1:2 for 60 minutes at 363 °K with evaporation, as a result of which 41.0% solutions of calcium-magnesium chlorate defoliant can be obtained.
ACKNOWLEDGEMENTS
- The authors acknowledge the immense help received from the scholars whose articles are cited and included in references to this manuscript. The authors are also grateful to the authors/ editors/publishers of all those articles, journals and books from where the literature for this article has been reviewed and discussed.In addition, the authors express gratitude to the head of the Fergana Polytechnic Institute and the scientific community of the Department of Chemical Technology for their assistance in carrying out this research work.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML