-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Materials and Chemistry
p-ISSN: 2166-5346 e-ISSN: 2166-5354
2019; 9(1): 13-22
doi:10.5923/j.ijmc.20190901.02

Entropy Terms in Statistical Thermodynamic Analysis Formula for Non-stoichiometric Interstitial Compounds
Nobumitsu Shohoji
LEN - Laboratório de Energia, LNEG - Laboratório Nacional de Energia e Geologia I.P., Lisboa, Portugal
Correspondence to: Nobumitsu Shohoji, LEN - Laboratório de Energia, LNEG - Laboratório Nacional de Energia e Geologia I.P., Lisboa, Portugal.
| Email: |  |
Copyright © 2019 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

A series of statistical thermodynamic analyses were made since 1974 for different types of non-stoichiometric interstitial compounds MXx under simplifying a priori assumption of constant interaction energy E(X-X) between nearest neighbour interstitial atoms X within a homogeneity composition range of MXx at arbitrary temperature T [K]. Mode of distribution of X atoms in interstitial sites in MXx lattice is represented by number θ of available interstitial sites for occupation by X atoms per M atom and the value of θ is determined to fulfil the a priori assumption. Mode of atomic configuration would yield major contribution to entropy term ∆S that appears in conventional thermodynamic expression of Gibbs free energy of formation, ∆G, in form of T∆S. In the statistical thermodynamic formulation, contribution of tightly bound electron appearing in form of RT ln fX where fX refers to atomic partition function of X atom in the MXx lattice and R the universal gas constant. Judging from this mathematical form of the term, R ln fX is considered to represent entropic contribution from tightly bound electron to X atom in MXx lattice. In the published series of works on statistical thermodynamic analysis for non-stoichiometric interstitial compounds, calculated values for R ln fX were reported but they were not reviewed with serious attention because R ln fX was considered merely as a secondary factor compared to principal factor E(X-M) referring to interaction energy between X and M in MXx lattice that represents enthalpy ∆H in conventional thermodynamic term. In this review article, consideration is given exclusively to the factor R ln fX evaluated in statistical thermodynamic approach to non-stoichiometric interstitial compounds.
Keywords: Entropy terms, Statistical thermodynamics, Interstitial compound, Non-stoichiometry
Cite this paper: Nobumitsu Shohoji, Entropy Terms in Statistical Thermodynamic Analysis Formula for Non-stoichiometric Interstitial Compounds, International Journal of Materials and Chemistry, Vol. 9 No. 1, 2019, pp. 13-22. doi: 10.5923/j.ijmc.20190901.02.
Article Outline
1. Introduction
- Statistical thermodynamics is a unique analysis tool to span a bridge between the experimentally measurable macroscopic thermodynamic state parameters such as temperature T, equilibrium partial pressure p(X2) of X2 gas and composition x in non-stoichiometric interstitial compound MXx consisting of metal M and interstitial element X and the non-measurable atomistic interaction energy parameters E(i-j) (i, j = M or X). Condensed phase MXx subjected to statistical thermodynamic analysis might be in either solid or molten state.Basic principles of statistical thermodynamics as well as practical analysis procedures are summarized in a classical text book authored by Fowler and Guggenheim [1].In a monograph published in 2013 entitled "Statistical Thermodynamic Approach to Interstitial Non-stoichiometric Compounds (Hydride, Carbide, Nitride, Phosphide and Sulphide)" [2], results of statistical thermodynamic analysis acquired on the basis of the simplifying a priori assumption of constant E(X-X) within a homogeneity composition range of MXx at arbitrary T were compiled [3-46] while a few more publications in this line of work arose thereafter [47-49]. In those publications, values for dissociation energy of X2 gas molecules, D(X2) [kJ·mol-1], characteristic temperature for rotation of X2 molecule, Θr [K], and characteristic temperature for vibration of X2 molecule, Θv [K], were taken from JANAF Thermochemical Tables [50] in the earlier works [3-43] or from its successor NIST-JANAF Thermochemical Tables [51] for the more recent calculations [44-49].Metal constituent M in non-stoichiometric interstitial compound MXx might be a single metal but might be binary substitutional alloy to be represented by A1-yBy or even multi-component alloy with number of metallic constituents being greater than 2. For such alloys represented by A1-yBy, statistical thermodynamic analysis results demonstrated that, depending on difference in affinity of X atom to constituent A and to constituent B, atom cluster might develop in the alloy lattice of A1-yByXx [9, 11, 16-19, 23, 25, 29, 33, 35-38, 40, 44, 46-49]. Statistical thermodynamic analysis was also made for alloy systems represented by MZzXx in which Z is interstitial constituent whose affinity to M is stronger than that of X to M and composition z might be pre-determined arbitrarily before measuring equilibrium pressure - temperature - composition (PTC) relationships between MZzXx and X2 gas [13, 31, 32, 34].Literature information for PTC data source used in the cited statistical thermodynamic analysis works is not given in the text below as the PTC data sources used for the calculations were cited in References section in each publication.
2. Statistical Thermodynamic Analysis Procedure
2.1. Fundamental Equations
- Generalized fundamental formulae proposed for this line of analysis of interstitial non-stoichiometric condensed phase MXx are as follows [2, 3, 11, 12, 18, 20, 23, 25, 36, 37, 49].
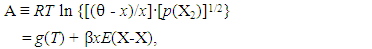 | (1) |
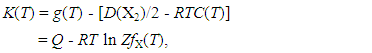 | (2) |
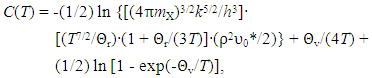 | (3) |
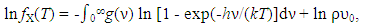 | (4) |
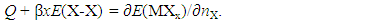 | (5) |
2.2. Partition Function
- Procedure to derive fundamental equation (1) is reviewed briefly in the following.Starting point of statistical thermodynamic analysis for non-stoichiometric interstitial alloy MXx is the compilation of partition function PF(MXx) for the condensed phase MXx and PF(X2) for ideal gas X2 at partial pressure p(X2) being in equilibrium with MXx at arbitrary T.Formula for PF(X2) at partial pressure p(X2) and at temperature T is readily available in a classical text book authored by Fowler and Guggenheim [1]. On the other hand, PF(MXx) has to be composed taking into account lattice structure of M and mode of distribution of X atoms over interstitial sites. Generalized formula for PF(MXx) is represented by
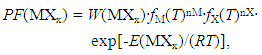 | (6) |
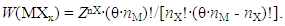 | (7) |
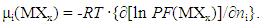 | (8) |
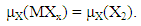 | (9) |
2.3. Analysis Procedure
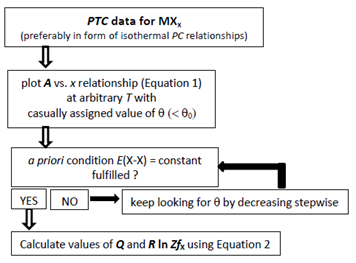
- At the onset of the analysis, isothermal A vs. x plots must be prepared from available isothermal PC relationship at arbitrary T using Eq. (1) by varying θ. As understood from Eq. (1), slope of isothermal A vs. x plot would become proportional to E(X-X). To fulfil the a priori assumption of constant E(X-X) within a homogeneity composition range of MXx at arbitrary T, θ yielding linear A vs. x relationship over the entire homogeneity composition range of MXx must be chosen for the subsequent calculations.Then, from the intercept g(T) calculated using Eq. (1), K(T) vs. T relationship must be drawn using Eq. (2). Term Q on the right hand side in Eq. (2) refers to extent of stabilization of atom X in the MXx lattice due to formation of X-M bonds in the MXx lattice while the coefficient R ln [ZfX(T)] to T refers to electronic contribution to entropy term in thermodynamic sense. In fact, partition function fX(T) of X atom in the MXx lattice is a T-dependent factor as represented by Eq. (4) but, as the T range of statistical thermodynamic analysis for MXx is typically no wider than 500 K, it has been a common practice to approximate fX(T) as a T-independent constant factor [2-49].For convenience of the readers, flow chart of the iterative determination procedure for a value of the parameter θ is presented as Fig. 1.
3. Values of the Term R ln ZfX(T) in MXx Lattice Evaluated by Statistical Thermodynamics
- Some representative calculation results for the term R ln ZfX(T) in MXx reported in the past publications are reviewed hereafter classifying M into different categories.
3.1. Estimated R ln ZfX(T) Values under Approximation of Constant fX with T
- In the standard statistical thermodynamic analysis carried out by the author, T-dependence of atomic partition function of fX(T) was not taken into account and fX(T) was assumed to hold T-independent constant value. For some MHx systems in which values of vibration frequency ν are available, attempts were made to evaluate R ln fX(T) as a function of T. The tentative calculation resuls for R ln fX(T) values as a function of T are reviewed later in the text in 3.2.
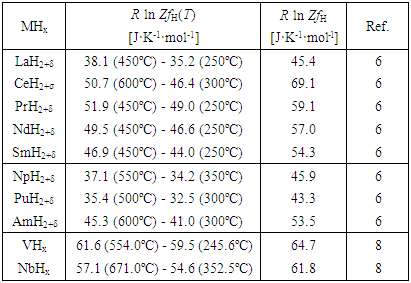
3.1.1. Primary Solid Solutions MHx
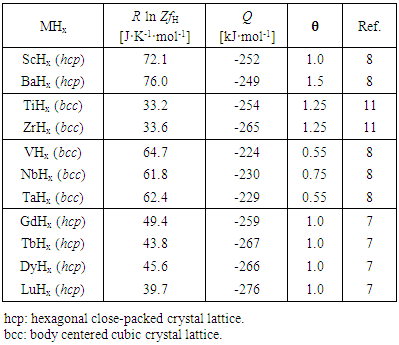
- Values of R ln ZfH and other parameters evaluated for primary solid solutions MHx are summarized in Table 1.
|
|
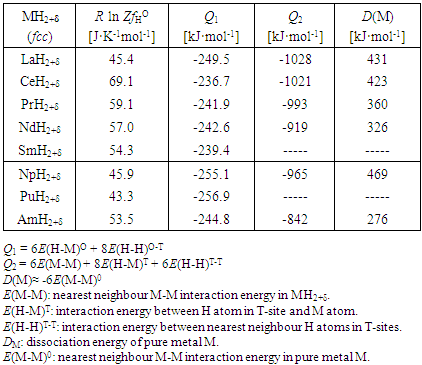
3.1.2. Hyper-stoichiometric Di-hydrides MH2+δ of Lanthanides and Actinide
- Analyses for hyper-stoichiometric di-hydrides MH2+δ of lanthanides (La, Ce, Pr, Nd, Sm) and actinides (Np, Pu, Am) with fcc lattice structure were made under assumption that H atoms up to H/M = 2.0 occupy the T-sites and H atoms exceeding H/M = 2.0 occupy randomly the O-sites [6]. Accepting this model, PF(MH2+δ) is represented by (in the original paper [6], the hyper-stoichiometric phase is represented by MH2+x instead of MH2+δ)
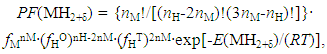 | (10) |
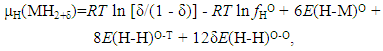 | (11) |
|
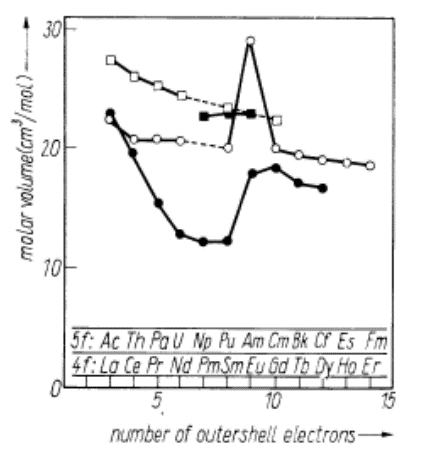 | Figure 2. Molar volume of some lanthanides (4f-group elements), actinides (5f-group elements) and their hydrides; M [52]: (○) 4f, (•) 5f. MH2.0 [53]: (□) 4f, (■) 5f. (Reproduced from Fig. 5 in [6]) |
3.1.3. Suppressed H Solubility for Va-group Alloys A1-yMyHx (A = V, Nb or Ta) by Alloying with Substitutional Metallic Constituent M (= Al, Co, Cr, Cu, Fe, Mo, Ni, Pd, Sn, Ru or W)
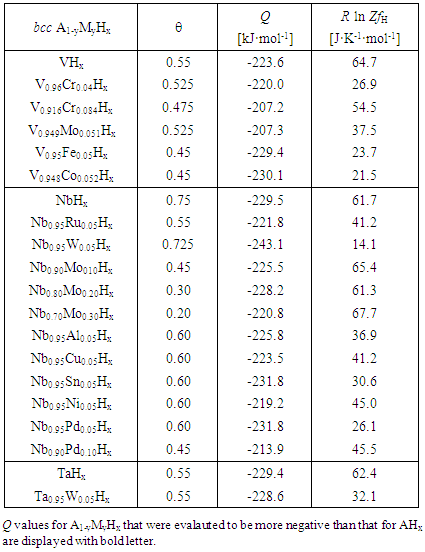
- Statistical thermodynamic evaluations for parameters, θ, Q and R ln ZfH, were made for A1-yByHx alloys of Va-group metals (A = V, Nb or Ta) through alloying with substitutional metallic constituents M (= Al, Co, Cr, Cu, Fe, Mo, Ni, Pd, Sn, Ru or W). The evaluation results are listed in Table 4 [49]. Graphical presentation of values for R ln ZfH and Q for Nb1-yMyHx alloys with suppressed H absorption from that in Nb through alloying with M (= Pd, Sn, Al, Cu, Ni or Mo) are reproduced in Fig. 3 [9].
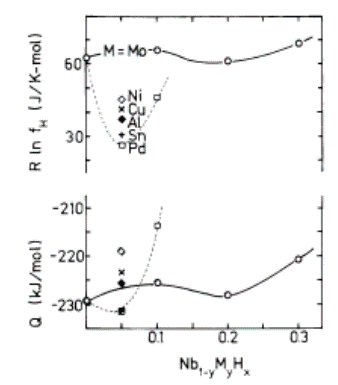 | Figure 3. Values of R ln ZfH and Q plotted as a function of y in bcc Nb1-yMyHx (M = Pd, Sn, Al, Cu, Ni or Mo). (Reproduced from Fig. 4 in [9]) |
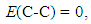 | (12) |
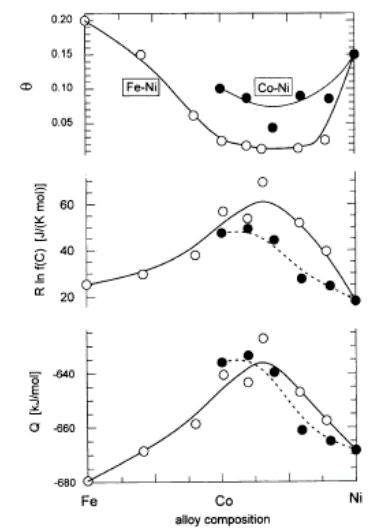 | Figure 4. Estimated values of θ, R ln ZfC and Q for fcc Fe1-yNiyCx and for fcc Co1-yNiyCx plotted as a function of alloy composition (mean number m of 3d electrons was 6 for Fe, 7 for Co and 8 for Ni). (Reproduced from Fig. 2 in [35]) |
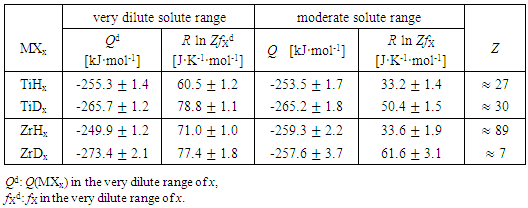
3.1.4. Influences of Concentration Range x and Isotope Effect of Solute Element X in MXx (M = Ti or Zr; X = H or D) on R ln ZfX
- Very dilute solution ranges of H and D (deuterium) in IVa-group metals, Ti and Zr, were analyzed under a priori assumption of
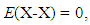 | (13) |
|
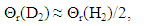 | (14) |
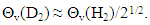 | (15) |
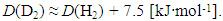 | (16) |
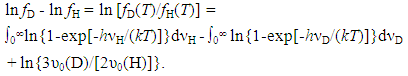 | (17) |
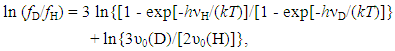 | (18) |
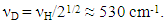 | (19) |
3.2. Attempts to Estimate R ln ZfX(T) Values Taking into Account T-dependence of fX(T)
- As represented by Eq. (4), expression for ln fX(T) is a function of T
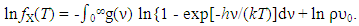 | (4) |
|
4. Concluding Remarks
- Characteristic features of entropy terms appearing in statistical thermodynamic analysis formula for non-stoichiometric interstitial compound MXx are reviewed.On undertaking the statistical thermodynamic analysis for MXx, essential first step is to compose plausible partition function PF(MXx) to MXx by taking realistic distribution model for interstitial non-metallic constituent X in MXx lattice. For this criterion to be fulfilled, it was proposed in the first publication [3] of this series of work to choose the number θ of available interstitial sites per M atom that appears in fundamental formula Eq. (1) in a way to yield constant E(X-X) at arbitrary T over entire homogeneity composition range of MXx. The system analyzed in [3] was hypo-stoichiometric nitride of chromium, CrN0.50-δ, and θ to fulfil the a priori assumption of constant E(N-N) was determined to be 0.5 and the analysis results looked realistic holding rational compatibility with the available thermodynamic parameter values for Cr2N phase. This choice of θ parameter value for analysis of CrN0.50-δ would mean that available sites for N atom occupation in hcp CrN0.50-δ lattice were O-sites and occupation of one O-site by N atom would block occupation by a neighbouring O-site by another N atom (i.e., Z = 2). Geometrically available number θ0 of available interstitial sites per M atom in close-packed MXx lattice (fcc or hcp) would be 1 if the O-sites are occupied or 2 if T-sites are occupied
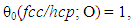 | (20) |
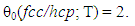 | (21) |
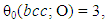 | (22) |
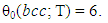 | (23) |
ACKNOWLEDGEMENTS
- Late Dr. Masahiro Katsura (†2017.01.31) is sincerely acknowledged for his patient guidance for the author to get acquainted with principles and analysis procedures in statistical thermodynamics. Although most of the works in this line were done by the author himself, there were occasional assistances provided for calculations by collaborators including Mrs. Teresa Marcelo, Mrs. Maria Cândida Monteiro Dias and Ms Sofia Figueiredo Marques. The author would like to thank an institutional colleague, Dr. Cristina Sena Ferreira, for her painstaking careful reading of the manuscript to point out several typographic errors contained in the original text. Long-term research collaborator, Dr. José Brito Correia, is sincerely acknowledged for his provision of information on chronological development and current status of research in high-entropy alloys.
Appendix / Symbols
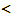 universal constants>R: universal gas constant (= 8.31451 [J·mol-1·K-1]),h: Planck constant (= 6.6260755 × 10-34 [J·s]),k: Boltzmann constant (= 1.380658 × 10-23 [J·K-1]),
universal constants>R: universal gas constant (= 8.31451 [J·mol-1·K-1]),h: Planck constant (= 6.6260755 × 10-34 [J·s]),k: Boltzmann constant (= 1.380658 × 10-23 [J·K-1]), 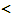 materials constants>mX: mass of X atom,ρ: nuclear spin weight,Θr: characteristic temperature for rotation of X2,Θv: characteristic temperature for vibration of X2,υ0*: electronic state of normal state of X2 molecule,D(X2): dissociation energy of X2 molecule per mole,β: factor determined from crystal structure consideration,θ0: geometrically available number of interstitial site per M in MXx,υ0: statistical weight of tightly bound electrons around X in MXx,ν: vibrational frequency of X atom in MXx lattice,g(ν): distribution function,
materials constants>mX: mass of X atom,ρ: nuclear spin weight,Θr: characteristic temperature for rotation of X2,Θv: characteristic temperature for vibration of X2,υ0*: electronic state of normal state of X2 molecule,D(X2): dissociation energy of X2 molecule per mole,β: factor determined from crystal structure consideration,θ0: geometrically available number of interstitial site per M in MXx,υ0: statistical weight of tightly bound electrons around X in MXx,ν: vibrational frequency of X atom in MXx lattice,g(ν): distribution function,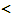 experimentally measurable macroscopic parameters> p(X2): equilibrium pressure of ideal gas X2,T: absolute temperature [K],x: composition (X/M atom ratio = nX/nM) in MXx,nX: number of X atoms in MXx lattice,nM: number of M atoms in MXx lattice,
experimentally measurable macroscopic parameters> p(X2): equilibrium pressure of ideal gas X2,T: absolute temperature [K],x: composition (X/M atom ratio = nX/nM) in MXx,nX: number of X atoms in MXx lattice,nM: number of M atoms in MXx lattice, atomistic parameters to be evaluated>Q: degree of stabilisation of X atom in MXx lattice with reference to isolated X and M atoms in vacuum,E(i-j): interaction energy between i and j atoms in MXx lattice,E(MXx): lattice energy,fX(T): partition function of X atom in MXx lattice, fM(T): partition function of M atom in MXx lattice, K & g: parameters determined by Equations, (1) & (2), from the experimental PTC data for an assigned value of θ,
atomistic parameters to be evaluated>Q: degree of stabilisation of X atom in MXx lattice with reference to isolated X and M atoms in vacuum,E(i-j): interaction energy between i and j atoms in MXx lattice,E(MXx): lattice energy,fX(T): partition function of X atom in MXx lattice, fM(T): partition function of M atom in MXx lattice, K & g: parameters determined by Equations, (1) & (2), from the experimental PTC data for an assigned value of θ,  a factor to be assigned a priori>θ: number of the interstitial sites per M atom available for occupation by X atoms in MXx lattice,
a factor to be assigned a priori>θ: number of the interstitial sites per M atom available for occupation by X atoms in MXx lattice, a resultant model parameter referring to extent of blocking of interstitial sites>Z: extent of blocking of interstitial sites by X in MXx lattice (= θ0/θ); that is, when one interstitial site in MXx is occupied by an X atom, (Z - 1) neighbouring interstitial sites are blocked from occupation by other X atoms.
a resultant model parameter referring to extent of blocking of interstitial sites>Z: extent of blocking of interstitial sites by X in MXx lattice (= θ0/θ); that is, when one interstitial site in MXx is occupied by an X atom, (Z - 1) neighbouring interstitial sites are blocked from occupation by other X atoms.
References
| [1] | R. H. Fowler and E. A. Guggenheim: Statistical Thermodynamics. Cambridge University Press, Cambridge, UK, 1949. |
| [2] | N. Shohoji: Statistical Thermodynamic Approach to Interstitial Non-stoichiometric Compounds (Hydride, Carbide, Nitride, Phosphide and Sulphide). Lambert Academic Publishing, Saarbrücken, Germany, 2013. ISBN: 978-3-659- 45506- 3. |
| [3] | N. Shohoji, M. Katsura and T. Sano: Statistical model for the non-stoichiometric Cr2N phase. J. Less-Common Met. 38 (1974) 59-74, DOI: 10.1061/0022-5088(74)90203-3. |
| [4] | N. Shohoji: Comments on "Hysteresis in metal hydride". J. Less-Common Met. 90 (1983) L5-L6, DOI: 10.1061/0022- 5088(83)910129-7. |
| [5] | N. Shohoji: On the construction of a statistical model for primary solid solutions of hydrogen in the group Va transition metals (vanadium, niobium and tantalum). J. Less-Common Met. 90 (1983) L27-L29. DOI: 10.1061/0022-5088(74) 90082-6. |
| [6] | N. Shohoji: Statistical thermodynamic approach to some hyperstoichiometric dihydrides of lanthanides (La, Ce, Pr, Nd, Sm) and actinides (Np, Pu, Am). Physica Status Solidi (B) 118 (1983) 811-822. DOI: 10.1002/pssb.2221180238. |
| [7] | N. Shohoji: Statistical thermodynamics of hydrogen solution in some lanthanides. Physica Status Solidi (B) 119 (1983) K87-K90. DOI: 10.1002/pssb.222190169. |
| [8] | N. Shohoji: Statistical thermodynamics of metal-hydrogen systems. J. Less-Common Met. 102 (1984) 53-65. DOI: 10.1016/0022-5088(84)90388-6. |
| [9] | N. Shohoji: Statistical model for the hydrogen solutions in bcc Nb1-yMy alloys (M = Al, Cu, Sn, Ni, Pd). Mater. Lett. 3 (1985) 206-208. DOI: 10.1016/0167-577X(85)90056-4. |
| [10] | N. Shohoji: Statistical thermodynamics of carbon solutions in metals. Mater. Chem. Phys. 13 (1985) 567-575. DOI: 10.1016/0254-0584(85)90006-9. |
| [11] | N. Shohoji: Statistical thermodynamics of the very dilute interstitial solid solutions. Z. Metallkde. 76 (1985) 192-197. |
| [12] | N. Shohoji: The application of statistical thermodynamics to interstitial solid solutions. J. Less-Common Met. 114 (1985) 249-256. DOI: 10.1016/0022-5088(85)90443-6. |
| [13] | N. Shohoji: Statistical thermodynamic study of the ternary compounds ThXyHx (X = C, N; y < 1, x < 2). J. Nucl. Mater. 127 (1985) 88-96. DOI: 10.1016/0022-3115(85)90064-2. |
| [14] | N. Shohoji: Interaction between hydrogen atoms in metals. J. Mater. Sci. Lett. 5 (1986) 522-524. DOI: 10.1007/BF01728678. |
| [15] | N. Shohoji: Comparative study of solubilities of hydrogen, nitrogen and carbon in α-iron. J. Mater. Sci. 21 (1986) 2147-2152. DOI: 10.1007/BF00547962. |
| [16] | N. Shohoji: Statistical thermodynamic analysis of phosphorus solubility in molten iron. Trans. Iron Steel Inst. Jpn 26 (1986) 194-197. DOI: 10.2355/isijinternational1986.26.194. |
| [17] | N. Shohoji: Statistical thermodynamics of sulphur solution in molten iron. Trans. Iron Steel Inst. Jpn 26 (1986) 547-550, DOI: 10.2355/isijinternational1986.26.547. |
| [18] | N. Shohoji: Statistical thermodynamic aspects of hydrogen in metals. Surface Coatings Technol. 28 (1986) 365-382, DOI: 10.1026/0257-8972(86)90093-9. |
| [19] | N. Shohoji: Statistical model for nitrogen solution in molten iron and molten iron alloys. Mater. Sci. Technol. 3 (1987) 43-48. DOI: 10.1179/mst.1987.3.1.43. |
| [20] | Shohoji, N. Carbon solubilities in iron at elevated temperatures analysed by statistical thermodynamics. Mater. Sci. Technol. 3 (1987) 404-410, DOI: 10.1179/mst.1987.3.6.404. |
| [21] | N. Shohoji and T. Marcelo: Tetragonality in crystal lattice of zirconium dihydride, J. Mater. Sci. Lett. 6 (1987) 1251-1253. DOI: 10.1007/BF01794578. |
| [22] | N. Shohoji: Estimation of carbon-metal interaction in the carbides of d-transition metals. Mater. Chem. Phys. 17 (1987) 391-398. DOI: 10.1016/0254-0584(87)90089-7. |
| [23] | N. Shohoji: Statistical model for molten Fe1-yCryNx (0.4 ≤ y ≤ 0.9). Mater. Sci. Technol. 4 (1988) 867-870. DOI: 10.1179/ mst.1988.4.10.867. |
| [24] | N. Shohoji and J. Botas: Glass-forming ability of multicomponent alloys viewed from statistical thermodynamic standpoint. J. Mater. Sci. Lett. 7 (1988) 903-905. DOI: 10.1007.BF00720724. |
| [25] | N. Shohoji: Clustering of atoms in molten Fe1-yTiyNx. Mater. Chem. Phys. 24 (1989) 163-173. DOI: 10.1016/0254- 0584(89)90055-2. |
| [26] | N. Shohoji: Unique features of hydrogen in palladium metal lattice: hints for discussing the possible occurrence of cold nuclear fusion. J. Mater. Sci. Lett. 9 (1990) 231-232. DOI: 10.1017/BF00727727. |
| [27] | N. Shohoji: Stability of interstitial elements in metal lattice evaluated by statistical thermodynamics. ISIJ Internat. (Successor to Trans. Iron Steel Inst. Jpn) 30 (1990) 472-474. DOI: 10.2355/isijinternational.30.472. |
| [28] | N. Shohoji and M. Katsura: Statistical thermodynamic appreciation of metal nitrides at elevated temperatures. J. Nucl. Mater. 170 (1990) 109-112. DOI: 10.1016/0022-3115(90) 90333-1. |
| [29] | N. Shohoji: Nitrogen solution in molten Fe1-yMy (M = Al, Mn) analyzed using statistical thermodynamics. Mater. Sci. Technol. 7 (1991) 213-217, DOI: 10.1179/mst.1991.7.3.213. |
| [30] | M. C. Monteiro Dias and N. Shohoji: Stability of hydrogen and nitrogen in VIa-group metals (Cr, Mo, W) and iron-group metals (Fe, Co, Ni) evaluated by statistical thermodynamics. J. Mater. Sci. 27 (1992) 5154-5158, DOI: 10.1007/BF02403809. |
| [31] | N. Shohoji: Statistical model for nitrogen solution in molten iron containing another interstitial constituent (carbon or silicon). Mater. Chem. Phys. 32 (1992) 153-159. DOI: 10.1016/ 0254-0584(92)90271-9. |
| [32] | M. C. Monteiro Dias and N. Shohoji: Atomic configuration in hexagonal-close-packed TiCzHx phase estimated by statistical thermodynamics. Mater. Chem. Phys. 39 (1995) 193-199. DOI: 10.1016/0254-0584(94)01429-K. |
| [33] | N. Shohoji: Statistical thermodynamic approach to carbon solubility in face centred cubic Fe1-yNiy alloy lattice. Mater. Sci. Technol. 12 (1996) 373-377. DOI: 10.1179/026708396790165867. |
| [34] | M. C. Monteiro Dias and N Shohoji: A theory of suppressed nitrogen solubility in Fe-Z-N ternary alloy systems in the relatively high range of concentration of Z (Z = Si or C). Mater. Chem. Phys. 50 (1997) 275-279, DOI: 10.1016/S0254-0584(97)01944-5. |
| [35] | N. Shohoji: Carbon solubility in face centred cubic Co1-yNiy alloy lattice analysed by statistical thermodynamics. Mater. Chem. Phys. 51 (1997) 265-268. DOI: 10.1016/S0254-0584(97)80316-1. |
| [36] | N. Shohoji: Atomic clustering in non-stoichiometric interstitial alloy systems evaluated by statistical thermodynamics -example cases of analysis of short-range ordering for molten Fe1-yMyNx (M = Cr, Ti, V, Mn, Al). Advances in Materials Engineering and Technology, Special Publication of Internat. J. Mater. Product Technol., SPM1, 2001, Inderscience Enterprises Ltd. Geneva, Switzerland, Vol. 1, pp.41-48. |
| [37] | N. Shohoji: Statistical thermodynamics as a tool for evaluating atom clustering around interstitial atom. Mater. Trans. 42 (2001) 2225-2231. DOI: 10.2320/matertrans.42.2225. |
| [38] | N. Shohoji and M. C. Monteiro Dias: Statistical thermodynamic approach to austenitic Fe1-yNbyNx system. Mater. Sci. Technol. 19 (2003) 429-434. DOI: 10.1179/026708303225009319. |
| [39] | N. Shohoji: Interaction energy parameters in hypo-stoichiometric mono-carbides, TiCx and NbCx, evaluated by statistical thermodynamics. Mater. Sci. Technol. 19 (2003) 1469-1472. DOI: 10.1179/026708303225006033. |
| [40] | N. Shohoji: M-C dipole formation in fcc (face centred cubic) Fe1-yMyCx solid solution (M = Ti, Nb). Mater. Sci. Technol. 20 (2004) 301-306. DOI: 10.1179/026708304225012297. |
| [41] | N. Shohoji and M. C. Monteiro Dias: Empirical expression of phosphorus solubility in molten Fe1-yCry expressed as functions of temperature and phosphorus activity. ISIJ Internat. 45 (2005) 1226-1231. DOI: 10.2355/isijinternational.45. 1226. |
| [42] | N. Shohoji and S. Figueiredo Marques: Statistical thermodynamic approach to molten Fe-Cr-P. Internat. J. Mater. Research (Successor to Z. Metallkde.) 99 (2008) 245-250. DOI: 10.3139/146.101630. |
| [43] | N. Shohoji: Hydrogen absorption in epitaxial bcc V (001) thin film analysed by statistical thermodynamics. Thin Solid Films 518 (2010) 7167-7173. DOI: 10.1016/j.tsf.2010.06.052. |
| [44] | N. Shohoji: Suppressed hydrogen solubility in body centred cubic Va-group metals (Nb and Ta) by alloying with W or Ru analysed on the basis of statistical thermodynamics. Internat. J. Mater. Eng. Technol. 7 (2012) 33-54. |
| [45] | N. Shohoji: Statistical thermodynamic analysis for hydrogen absorption behaviour in a four monolayers (4 ML) thick bcc vanadium (110) superlattice being in contact with molybdenum layer. Mater. Trans. 53 (2012) 1273-1277. DOI: 10.2320/matertrans.M2012071. |
| [46] | N. Shohoji: Statistical thermodynamic analysis for isothermal hydrogenation performances of Mg2-yPryNi4 intermetallics (y = 0.6, 0.8, 1.0). Internat. J. Mater. Chem. 2 (2012) 90-100. DOI: 10.5923/j.ijmc.20120203.02. |
| [47] | N. Shohoji: Suppressed hydrogen (H) solubility in body centered cubic vanadium (V) by alloying with molybdenum (Mo), chromium (Cr), Iron (Fe) or cobalt (Co) appreciated in terms of statistical thermodynamics. Mater. Trans. 57 (2016) 321-328. DOI: 10.2320/matertrans.M2015415. |
| [48] | N. Shohoji: Proposing design guideline for hydrogen permeation membrane alloy based on Va-group metals (V, Nb and Ta) taking into account interaction energy parameter evaluated by statistical thermodynamics. Internat. J. Mater. Eng. Technol. 15 (2016) 75-92. DOI: 10.17654/MT015010075. |
| [49] | N. Shohoji: Characterizing atomic interactions in interstitial non-stoichiometric compounds by statistical thermodynamics: engineering usage of estimated values of statistical thermodynamic parameters. J. Modern Phys. 8 (2017) 365-381. DOI: 10.4236/jmp.2017.83025. |
| [50] | D. R. Stull, H. Prophet and G. C. Sinke G.C. (Ed.): JANAF Thermochemical Tables; Joint Army, Navy and Air Force, Dow Chemicals Co., Midland, MI, USA, 1965. |
| [51] | M. W. Chase Jr.: NIST-JANAF Thermochemical Tables, 4th Edition; J. Phys. Chem. Ref. Data, Monograph No. 9, Amer. Chem. Soc. and Amer. Inst. Phys., 1998. |
| [52] | S. Imoto: Electronic structure of actinide metals and semi-metallics. J. Atom. Energy Soc. Jpn. 20 (1978) 694-702. DOI: 10.3327/jaesj.20.694. |
| [53] | C. E. Messer and M. K. Park: Dissociation pressures and related thermodynamic functions and hydrogen solution parameters in the systems PrH2-PrH3, NdH2-NdH3, and SmH2-SmH3. General considerations for the related lanthanide and actinide hydride systems. J. Less-Common Met. 26 (1972) 235-246, DOI: 10.1016/0022-5088(72)90043-4. |
| [54] | F. D. Rossini, D. D. Wagman, W. H. Evans, S. Levine and I. Jaffe, (Ed.): Selected Values of Chemical Thermodynamic Properties, N.B.S. Circular 500 - Part I, USA, 1961. |
| [55] | J. J. Rush and H. E. Flotow: Vibration spectra of vanadium hydride in three crystal phases by inelastic neutron scattering. J. Chem. Phys. 48 (1968) 3795-3804. DOI: 10.1063/1.1669686. |
| [56] | N. A. Chernoplekov, M. G. Zemlyanov, V. A. Somenkov and A. A. Chertkov:. Study of the dynamics of group V transition-metal hydrides by means of inelastic neutron scattering. Sov. Phys. - Solid State 11 (1970) 2343-2349. |
| [57] | R. Yamada, N. Watanabe, K. Sato, H. Asano and M. Hirabayashi: Localized modes in tantalum hydrides studied by neutron inelastic scattering. J. Phys. Soc. Jpn 41 (1976) 85-90. DOI: 10.1143/JPSJ.41.85. |
| [58] | B. Cantor, I. T. H. Chang, P. Knight and A. J. B. Vincent: Microstructural development in equiatomic multicomponent alloys. Mater. Sci. Eng. A 375-377 (2004) 213-218. DOI: 10.1016/j.mesa.2003.10.257. |
| [59] | J. W. Yeh, S. K. Chen, S. J. Lin, J. Y. Gan, T. S. Chin, T. T. Shun, C. H. Tsau and S. Y. Chang: Nanostructured high-entropy alloy with multiple principal elements: novel design concepts and outcomes. Adv. Eng. Mater. 6 (2004) 299-303. DOI: 10.1002/adem.200300567. |
| [60] | S.-L. Wei, H. Feng and C. C. Tasan: Metastability in high-entropy alloys: a review. J. Mater. Res. 33 (2018) 2924-2937. DOI: 10.1557/jmr.2018.306. |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML