1. Introduction

The 5-membered nitrogen heterocyclic rings are structural fragments in a number of biologically active compounds [1], pesticides [2], pigments and other substances used in industry [3, 4].

One of the interesting pesticides is 3-Amino-1,2,4-triazole. Probably the most dramatic effect of amino-triazole on growing plants is its interference with chlorophyll formation. This property has simulated the investigation of the compound as a herbicide, cotton defoliant, and inhibitor of second growth. Triazole is a promising substance for commercial control of perennials such as Canada thistle [5], quack-grass [6], Johnson grass [7], nut grass [8], and woody plants like poison ivy and poison oak [9].

The pesticides contained in soil often react with metal ions. The information about the geometry and stability constants of such complexes would provide a possibility to describe pesticides propagation in soil and subterranean water, as well as the mechanisms of their transportation in plants.

In a previous work, we have studied amino-triazole complex formation in aqueous solutions with ions contained in soil as macro-components (Fe³⁺, Al³⁺, Ca²⁺) and micro-components (Cu²⁺, Co²⁺, Cd²⁺, Ni²⁺, Zn²⁺ and Hg²⁺) [10].

The aims of the presented study are to determine the geometric and electronic structure of [Me(3-Amino-1,2,4-triazole)₂]²⁺ complex ions (Me =Zn, Cu, Co, Ni and Cd) in water phase and to establish the relationship between the stability constants of the complexes and the electronic properties of the complex ions by quantum chemical calculations.

2. Computational Methods

The full optimization of 3-Amino-1,2,4-triazole was carried out by Hartree-Fock (HF) and Density Functional Theories (DFT) methods, using Gaussian 03 software [11] at the B3LYP level with 6-31G(d,p) basis set. All calculations were converged to 10^–8 a.u. Vibration frequencies were also calculated to the structure with optimized geometry and no imaginary frequency were obtained, so the stationary point correspond to the minima of the potential energy surface.

An effective method for studying the reaction behavior of molecules is the measuring of their electrostatic potential. The electrostatic potential of 3-Amino-1,2,4-triazole was calculated by DFT method at the B3LYP level with 6-31G(d,p) basis sets. The electrostatic potential is widely used in studies on biological systems to predict the reactivity of numerous chemical systems in electro- and nucleophilic reactions [12]. In order to characterize the electronic population on each atomic centre a Mulliken population analysis [13] was carried out for 3-Amino-1,2,4-triazole. The geometric optimization of [Me(3-Amino-1,2,4-triazole)₂]²⁺ complex ions (Me = Zn, Cu, Co, Ni, and Cd) in water phase was done by DFT using Becke’s three-parameter hybrid functional with 6-31G(d,p)basis set and LANL2DZ effecitive core potential for the metals - Co, Cd, and Ni. To take into account the effect of the solvent by self-consistent reaction field (SCRF) the method of Onsager was used [14]. The Onsager model places the solute in a spherical cavity within the solvent reaction field. The solvent is treated as polarizable continuum with a dielectric constant - , instead of explicit solvent molecules. The charge distribution of the solute polarizes the solvent producing a reaction potential. The reaction potential of solvent alters the solute. This interaction is represented by Hamiltonian containing the solvent reaction potential. All calculations are for complexes at ratio Me: L = 1:2.

The software packages HyperChem 5.0 [15] and Molekel 5.4 [16] were used for data preparation and visualization of the results.

3. Results and Discussion

The visualization of the optimized geometrical structure and atomic labeling of 3-Amino-1,2,4-triazole are presented in Figure 1.To choose suitable calculation method, geometric optimization of 3-Amino-1,2,4-triazole carried out and the results were compared with theexperimental results obtained as it is given in Table 1.

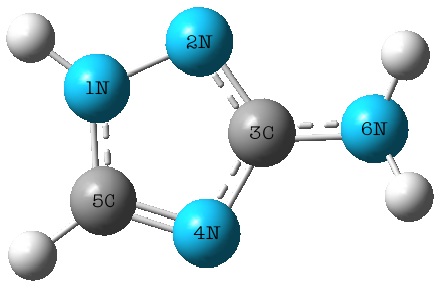Figure 1. Optimized geometrical structure and atomic labeling of 3-Amino-1,2,4-triazole

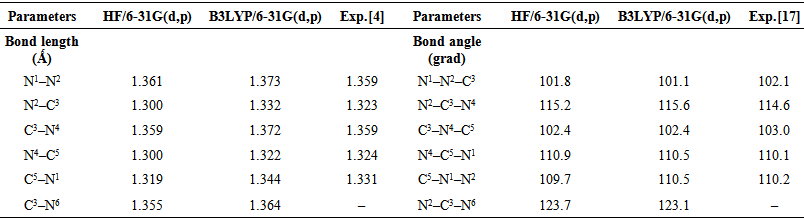Table 1. Optimized geometrical parameters of 3-Amino-1,2,4-triazole

From the data, presented in Table 1 it can be seen that the HF and DFT methods produce structural parameters which are in good agreement with the experimental Rë structure analyses, reported earlier for similar compounds [17]. Despite the fact that the reference compound has either an H atom or a CH₃- group instead of the NH₂- one, the average bond length divergence between theoretical and experimental data are much better for B3LYP.

The molecular electrostatic potential (MEP) is a property that the electrons and nuclei of a molecule create at each point r in the surrounding space [12]. Electrostatic potential provides very useful information to explain hydrogen bonding, reactivity and structure–activity relationship of molecules and correlates with dipole moment, electronegativity, partial charges and site of chemical reactivity of the molecule. It gives a visualization to understand the relative polarity of a molecule. The regions with negative MEP, correspond to the areas of high electron density representing a strong attraction between the proton and the points, on the molecular surface have the brightest red color. The positive valued regions, areas of lowest electron density, have deep blue to indigo color indicating the regions of maximum repulsion. The electron density isosurface onto which the electrostatic potential surface was mapped and it is shown in Figure 2 for 3-Amino-1,2,4-triazole, calculated by DFT method with 6-31G(d,p) basis set. The red colored surface areas show the most negative molecular electrostatic potential while dark blue areas – the most positive one. As can be seen, the region around N⁴ is rich in electrons. Since the electrostatic potential there has the most negative values, the metal ion coordinates with this atom.

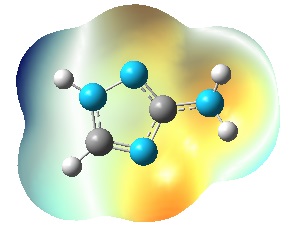Figure 2. Electrostatic potential on the surface of3-Amino-1,2,4-triazole

The quantum chemical calculations provide possibility to estimate the net atomi charges – q, localized at the corresponding atoms as a result of the redistribution of the electrons in the molecule. Despite that they are neither experimentally observed nor related to some physical property, they allow revealing the distribution of electron density in a system of interconnected atoms and predicting some chemical properties of the molecule. The net atomic charges values were obtained by the Mulliken population analysis [13] with Hartree-Fock (HF) and Density Functional Theories (DFT)methods with 6-31G(d,p) basis set.

The net atomic charges of the heteroatoms (Table 2) show that the N¹, N², N⁴ and N⁶ centers of triazole have negative charge values of –0.329, –0.367, –0.503 and –0.676, respectively.

Table 2. Mulliken atomic charges of 3-Amino-1,2,4-triazole

As it can be seen from the calculations of the electrostatic potential and the atomic charges carried out that the site most suitable for creation of a coordination bond is N⁴.

It is well known that DFT methods work better for systems containing transition metal atoms. For these reasons, we used B3LYP level with 6-31G(d,p) orbital basis set for the complexes.

The optimized geometrical parameters of [Me(3-Amino-1,2,4-triazole)₂]²⁺ complex ions in water phase are shown in Table 3. The visualization of the optimized geometrical structure and atomic labeling of [Me(3-Amino-1,2,4-triazole)₂]²⁺ complex ions are presented in Figure 3.

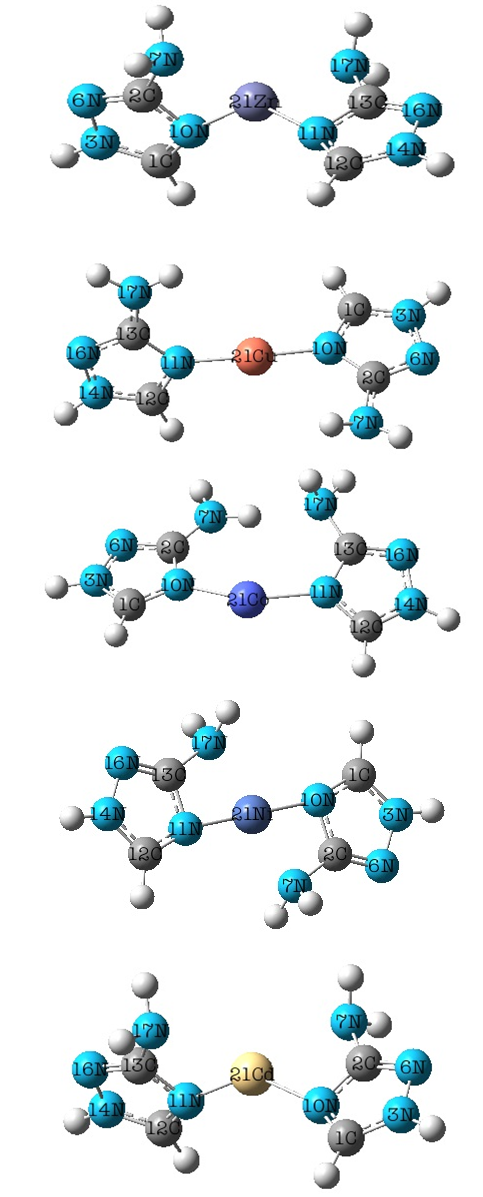Figure 3. Optimized geometrical structures and atomic labeling of [Me(3-Amino-1,2,4-triazole)2]2+ complex ionsin water phase

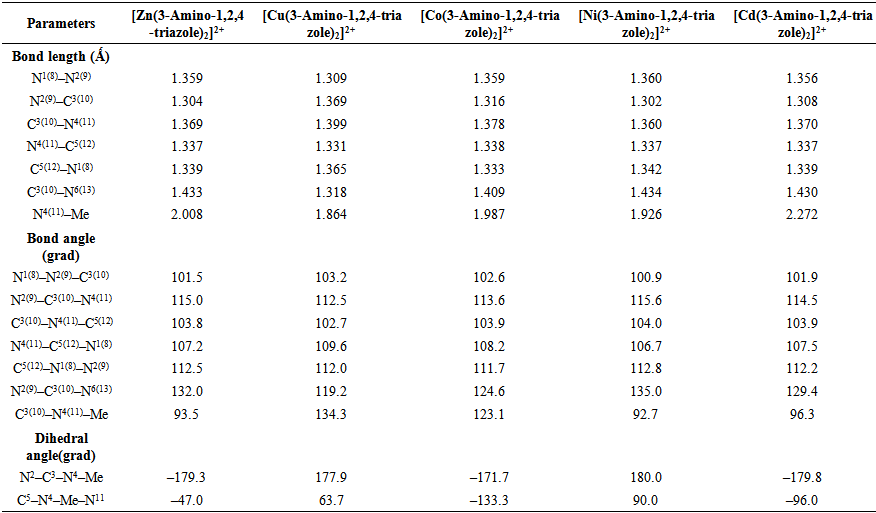Table 3. Optimized geometrical parameters of [Me(3-Amino-1,2,4-triazole)2]2+complex ions in water phase

The calculated bond orders are reported in Table 4. Obviously, the triazole bond orders are in the range 1,128 -1,766. These bond order values suggest a relatively strong aromatic character for the five-membered ring of triazole.

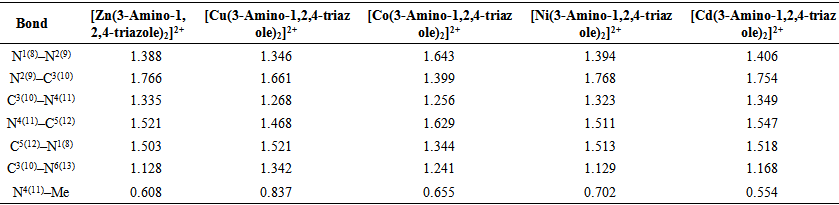Table 4. Bond orders of [Me(3-Amino-1,2,4-triazole)2]2+complex ions in water phase

The calculated electronic properties of the complex ions are shown in Table 5. The highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) are the main orbitals that plays an important role in chemical stability [18]. The HOMO exhibits the ability to donate an electron and LUMO as an electron acceptor serves the ability to obtain an electron. The HOMO and LUMO energy calculated by B3LYP/6-311G (d,p) level of theory show the energy gap which reflects the chemical activity of the molecule. On the basis of HOMO-LUMO energies global reactivity descriptors, such as the energies of frontier molecular orbitals (E_HOMO, E_LUMO), energy band gap (E_HOMO–E_LUMO), electronegativity(χ), chemicalpotential(µ), global hardness(η), global softness(S) and global electrophilicity index(ω), which describe the electrophilic behaviour, were calculated for [Me(3-Amino-1,2,4-triazole)₂]²⁺ complexions using Eqs. (1)–(5) [19-23]:

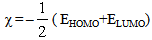(1)

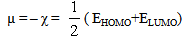(2)

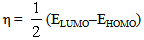(3)

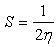(4)

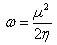(5)

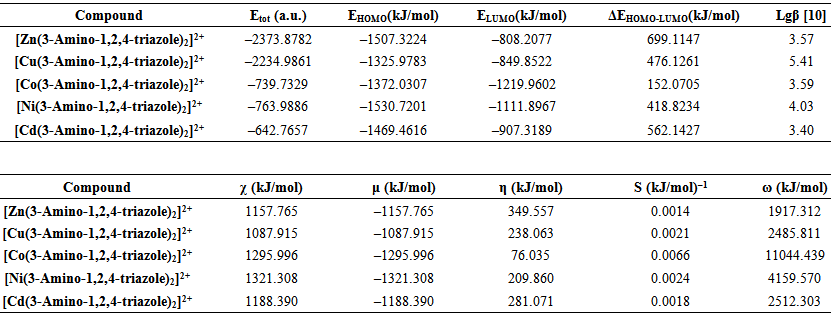Table 5. Calculated electronic properties of [Me(3-Amino-1,2,4-triazole)2]2+complex ions in water phase

The relationship between the stability constants of the complexes and the electronic properties of the complex ions were examined. The relationship between the stability constants of the complexes and calculated bond ordersMe– L are shown in Figure 4.

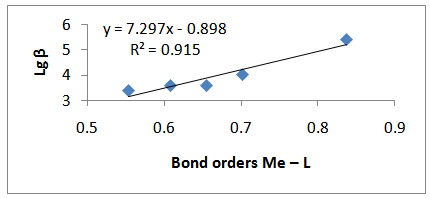Figure 4. Relationship between the stability constants of the complexes and the calculated bond ordersMe– L

From the presented Figure 4, it can be observed that the stability constants of the complexes correlate well with the calculated bond orders Me – L.

4. Conclusions

The pesticides contained in soil often react with metal ions. The information about the geometry and stability constants of such complexes would provide a possibility to describe pesticides propagation in soil and subterranean water, as well as the mechanisms of their transportation in plants. The geometric optimization of 3-Amino-1,2,4-triazole was done by Hartree-Fock (HF) and Density Functional Theories (DFT) at the B3LYP level with 6-31G(d,p) basis set. From the calculated electrostatic potential and the net atomic charges of 3-Amino-1,2,4-triazole was found that the site most suitable for creation of a coordination bond is N⁴. The geometric optimization of [Me(3-Amino-1,2,4-triazole)₂]²⁺ complex ions (Me = Zn, Cu, Co, Ni, and Cd) was done in water phase by DFT using Becke’s three-parameter hybrid functional with 6-31G(d,p) basis set and LANL2DZ effecitive core potential fot the metals - Co, Cd, and Ni. The bond orders and the electronic properties of the complex ions were calculated. The relationship between the stability constants of the complexes and the electronic properties of the complex ions were examined. It was found that the stability constants of the complexes correlate well with the calculated bond orders Me–L.