-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Materials and Chemistry
p-ISSN: 2166-5346 e-ISSN: 2166-5354
2014; 4(3): 51-64
doi:10.5923/j.ijmc.20140403.02
Molecular Structure and Vibrational Analysis of 2-Amino- 5-(m-Nitrophenyl)-1,3,4-Thiadiazole by DFT Calculations
Mahesh Pal Singh Yadav, Anuj Kumar
Department of Physics, Jaypee University of Engineering and Technology, Raghogarh, Guna, 473226, India
Correspondence to: Anuj Kumar, Department of Physics, Jaypee University of Engineering and Technology, Raghogarh, Guna, 473226, India.
| Email: |  |
Copyright © 2014 Scientific & Academic Publishing. All Rights Reserved.
The 1,3,4-thiadiazole nucleus is one of the most important and well-known heterocyclic nuclei, which is a common and integral feature of a variety of natural products and medicinal agents. The role of thiadiazole and their derivatives has been very well established as pharmacologically significant scaffolds. Introduction of a nitro group into the benzene ring is of particular interest both for the elucidation of the influence of electron-withdrawing substituents on the reactivity of donor centers of heterocyclic compounds and for the subsequent synthesis of thiadiazole derivatives based on the reduced nitro group. The effect on delocalization of electron density (ED) and donor acceptor interaction due to change in substituents affects pharmacological activities significantly.In the present work, in an attempt to understand, the structure activity relation in an 1,3,4-thiadiazole we report optimized molecular structure confirmed by predictive vibrational spectra (IR/Raman spectra) and electronic behavior of one of the thiadiazole derivative 2-amino-5-(m-nitrophenyl)-1,3,4-thiadiazole. The calculations were made by density functional theory (DFT) using Becke’s three-parameter hybrid functional (B3LYP) at various level of theory. The natural bond orbital analysis (NBO) has been performed in order to study the intramolecular bonding interactions among bonds and delocalization of unpaired electrons. These intramolecular charge transfer (n–σ*, n–π* and π-π*) can induce biological activities such as antimicrobials, anti-inflammatory, anti-fungal etc. in the molecule. Calculated band gap of 2.426 eV and global reactivity descriptors using HOMO-LUMO energies explain chemical and biological activity.
Keywords: 1,3,4-Thiadiazole, Density functional theory, Structure activity relation, Charge transfer, IR/Raman spectra, HOMO-LUMO, Natural bond analysis (NBO)
Cite this paper: Mahesh Pal Singh Yadav, Anuj Kumar, Molecular Structure and Vibrational Analysis of 2-Amino- 5-(m-Nitrophenyl)-1,3,4-Thiadiazole by DFT Calculations, International Journal of Materials and Chemistry, Vol. 4 No. 3, 2014, pp. 51-64. doi: 10.5923/j.ijmc.20140403.02.
Article Outline
1. Introduction
- Heterocyclic compounds are ring compounds containing carbon and other element, the component being oxygen, nitrogen and sulphur. Thiadiazoles are heterocyclic compounds containing two nitrogen atoms and one sulfur atom as part of the aromatic five-membered ring. 1,3,4- thiadiazole are important because of their versatile biological actions[1]. There are number of thiadiazoles which contain the nitrogen in different positions such as 1,2,3-thiadiazole [2], 1,2,4-thiadiazole [3], 1,3,4-thiadiazole [4] and 1,2,5-thiadiazole [5] and their benzo derivatives [6] etc. 1,3,4-thiadiazole Derivatives shows a wide range of biological, pharmacological, and antileukemic activities [7-9]. Large number of such compounds have been synthesized and studies for their spectroscopic behavior and biological activity [3-6, 10].We have selected 2-amino-5-(m-nitrophenyl)-1,3,4 -thiadiazole, abbreviated as AMNT, one of the simplest 1,3,4-thiadiazole derivative for our study. To the best of our knowledge, despite of potential pharmacological applications, this molecule is not undergone any comprehensive stereoelectronic and spectroscopic studies. 2-amino-5-(m-nitrophenyl)-1,3,4- thiadiazole showed monoclinic packing having cell parameter a = 11.832 Å, b = 9.862 Å, c = 8.353 Å, V = 913.63 Å3, dcalcd = 1.212 g cm–3 with space group P21/c [11]. Introduction of a nitro group into the benzene ring is of particular interest both for the elucidation of the influence of electron-withdrawing substituents on the reactivity of donor centers of heterocyclic compounds and for the subsequent synthesis of thiadiazole derivatives based on the reduced nitro group. Replacing the substituent in the phenyl group at position 3 of the 1,3,4-thiadiazole compounds with electron withdrawing groups, like halogens, nitriles, carbonyls etc. leads to affect biological activities [9].In the present study, in an attempt to understand the structure property relation, the stereoelectronic interactions associated with the structural properties of 2-amino -5-(m-nitrophenyl)-1,3,4-thiadiazole were investigated computationally using density functional theory (DFT) and ab initio methods. Therefore, we report optimized molecular structure confirmed by predictive vibrational spectra (FTIR/Raman) and physicochemical behavior for 2-amino-5-(m-nitrophenyl)-1,3,4-thiadiazole. In order to find conformational stability of the 2-amino-5-(m- nitrophenyl)-1,3,4-thiadiazole molecule, a potential energy scan is performed, and the corresponding relative energies were compared. The equilibrium geometry, harmonic vibrational wavenumbers, electrostatic potential surfaces, absolute Raman scattering activities and infrared absorption intensities have been calculated by DFT [12] with B3LYP functionals using various basis sets and HF/6-311G(d,p) with the help of Gaussian 09W package [13]. The calculated vibrational spectra were analyzed on the basis of the potential energy distribution (PED) of each vibrational mode which allowed us to obtain a quantitative as well as qualitative interpretation of the infrared and Raman spectra. To understand structure property relationship, HOMO-LUMO, electrostatic potential surface and natural bond orbitals have been obtained. Natural bond orbital analysis has been carried out to understand the nature of different interactions responsible for the electron delocalization and the intra-molecular charge transfer between the orbitals. These intra-molecular charge transfer (n–σ*, n–π* and π-π*) can induce biological activities such as antimicrobials, anti-inflammatory, anti-fungal, antibiotic, diuretic, antidepressant, anticancer, anticonvulsants, etc. in the molecule.
2. Computational Details
- Computational aspects for geometry optimization and electronic structure of the stable conformers of the molecule have been done by density functional theory [12] by using the Gaussian 09W program package[13] employing different basis sets and Becke’s three parameter (local, nonlocal, Hartree–Fock) hybrid exchange functionals with Lee–Yang–Parr correlation functionals (B3LYP) [14-16]. Infrared absorption intensities and Raman intensities have been calculated in the harmonic approximation with the help of same functional and basis sets as used for the optimized geometries, from the derivatives of the dipole moment and polarizability of each normal mode, respectively. The normal-mode analysis was used to calculate PED for each of the internal coordinates using no symmetry [17-18]. In order to prepare PED a complete set of 57 internal coordinates was defined using Pulay’s recommendations [19, 20]. The vibrational assignments of the normal modes were proposed on the basis of the PED calculated using the program GAR2PED [21]. Calculated DFT vibrational wavenumbers are known to be higher than the experimental wavenumbers as the anharmonicity effects are neglected. Therefore, wavenumbers obtained by DFT were scaled down by the wavenumber linear scaling procedure (WLS) νobs = (1.0087–0.0000163νcalc.) νcalc. cm-1 [22]. The WLS method using this relationship predicts vibrational wavenumbers with high accuracy and is applicable to a large number of compounds, except for those where the effect of dispersion forces is significant. All the calculated vibrational wavenumbers reported in this study are the scaled values. In order to investigate intra-molecular charge transfer interactions, rehybridization and delocalization of electron density within the molecule, the natural bonding orbitals (NBO) analysis has been performed. The main natural orbital interactions were analyzed on the basis of NBO calculations done at DFT/B3LYP level using Gaussian 09W package. In the NBO analysis [23, 24], the electronic wave functions are interpreted in terms of a set of occupied Lewis-type (bond or lone pair) and a set of unoccupied non-Lewis (antibond or Rydberg) localized NBO orbitals. Delocalization of electron density (ED) between these orbitals corresponds to a stabilizing donor–acceptor interaction. The second-order perturbation theory has been employed to evaluate the stabilization energies of all possible interactions between donor and acceptor orbitals in the NBO basis. The delocalization effects can be estimated from off-diagonal elements of the Fock matrix in the NBO basis.
3. Results and Discussion
3.1. Geometry Optimization
- The theoretical structure of title molecule have been calculated by DFT using B3LYP functional having extended basis sets 6-311++G(d,p), 6-311+G(d,p), 6-311G(d,p) and HF/6-311G(d,p) with the help of Gaussian 09W package and geometry obtained from B3LYP/6-311++G(d,p) is shown in Fig.1.
 | Figure 1. Optimized structure of AMNT at the B3LYP/6-311++G(d;p) level of theory |
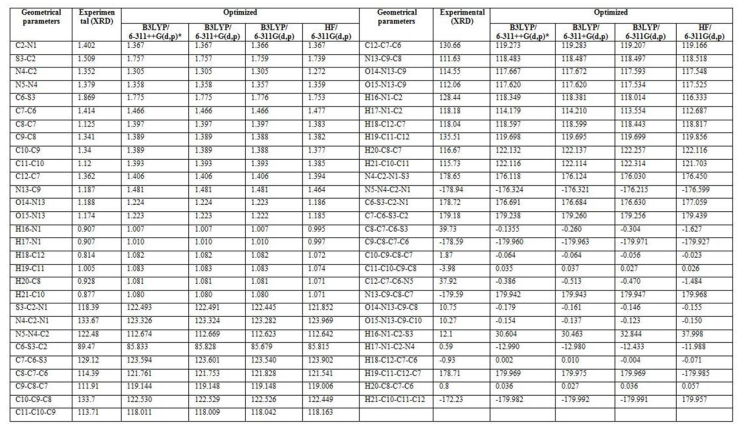 | Table 1. Optimized geometrical parameters of AMNT by DFT in comparison with XRD data |
3.2. Potential Energy Scan Studies
- In order to investigate all possible conformations of 2-amino-5-(m-nitrophenyl)-1,3,4-thiadiazole, a detailed potential energy scan was performed for the dihedral angle ϕ(C12–C7–C6–S3) at B3LYP/6-311++g(d,p) level of theory with constraint nosymmetry. The scan studies was obtained by minimizing the potential energy in all geometrical parameters by varying the torsion angles at a step of 5° in the range of 0–360° rotation around the bond. The variations of the potential energy change from its equilibrium with the torsional perturbation are presented in Fig. 2. The PES scan revealed that the 2-amino-5- (m-nitrophenyl)-1,3,4 -thiadiazole molecule may have less stable conformer at torsion angle (C12–C7–C6–S3) equal to -5.23709° having energy -1076.029 Hartree (-2825114.354 kJ/mol). The most stable equilibrium state belongs to (C12–C7–C6–S3) =179.862° and potential energy equal to -1076.309 Hartree (-2825851.595 kJ/mol).
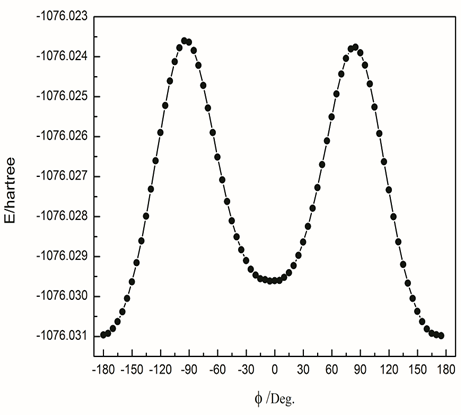 | Figure 2. Potential energy scan of AMNT about dihedral angle (C12–C7–C6–S3) at B3LYP/6-311++g(d,p) level of theory |
3.3. Natural Bond Orbital Analysis
- NBO analysis is an efficient method for study of the intramolecular and intermolecular bonding and interactions among bonds. This analysis also provides the study of filled NBOs (donors) and empty NBOs (acceptors) and their interactions with the stabilization energy E(2) resulting from the second-order perturbation theory. The larger the E(2) value, the more intensive is the interaction between electron donors and acceptors, i.e. the more electron donating tendency from electron donors to acceptors and the greater the extent of conjugation of the whole system. This interaction results a loss of occupancy from the concentration of electron NBO of the idealized Lewis (bond or lone pair) structure into an empty (anti-bond or Rydberg) non-Lewis orbital. For each donor (i) and acceptor (j), the stabilization energy E(2) associated with the delocalization i – j is estimated as [23, 27, 17]:
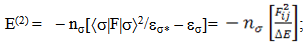 | (1) |
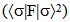 is the Fock matrix element which corresponds to i and j NBO orbitals.
is the Fock matrix element which corresponds to i and j NBO orbitals. 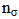 is the population of the donor
is the population of the donor 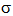 orbital,
orbital, 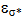 and
and 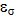 are the energies of
are the energies of  and
and  NBOs. NBO calculations were performed using the NBO 5.9 program as implemented in the Gaussian 09 package at the DFT/B3LYP/6-311++G(d,p) level of the theory. The second-order perturbation theory analysis of Fock matrix in NBO basis of AMNT molecule display strong intra-molecular conjugative and hyperconjugative interactions and demystify the rehybridization and delocalization of electron density within the molecule. Some important interactions between Lewis and non-Lewis orbitals along with their interacting stabilization energies are shown in Table-2.
NBOs. NBO calculations were performed using the NBO 5.9 program as implemented in the Gaussian 09 package at the DFT/B3LYP/6-311++G(d,p) level of the theory. The second-order perturbation theory analysis of Fock matrix in NBO basis of AMNT molecule display strong intra-molecular conjugative and hyperconjugative interactions and demystify the rehybridization and delocalization of electron density within the molecule. Some important interactions between Lewis and non-Lewis orbitals along with their interacting stabilization energies are shown in Table-2.
|
3.4. Molecular Electrostatic Potential
- Various weak interactions in 2-amino-5- (m-nitrophenyl)- 1,3,4-thiadiazole molecule, such as C–H… and weak hydrogen-bonding interactions have very important significance in determining stability of the molecule. The presence of amino and nitro group leads to the electronic coupling between ring electrons and nitrogen lone pair electrons which provides stabilization to the molecular structure and enhance its antilukemic properties. Hence it is important to study the electrostatic potential distribution in the molecule. The molecular electrostatic potential (MEP) is a property that the electrons and nuclei of a molecule create at each point r in the surrounding space [28]. Electrostatic potential provides very useful information to explain hydrogen bonding, reactivity and structure–activity relationship of molecules and correlates with dipole moment, electronegativity, partial charges and site of chemical reactivity of the molecule. It gives a visualization to understand the relative polarity of a molecule. The regions with negative MEP, correspond to the areas of high electron density representing a strong attraction between the proton and the points, on the molecular surface have the brightest red color. The positive valued regions, areas of lowest electron density, have deep blue to indigo color indicating the regions of maximum repulsion. The electron density isosurface onto which the electrostatic potential surface has been mapped is shown in Fig. 3 for 2-amino-5- (m-nitrophenyl)-1,3,4-thiadiazole. The different values of the electrostatic potential at the surface are represented by different colors; yellow represents regions of most negative electrostatic potential, blue represents regions of most positive electrostatic potential over the amino group and green represents regions of zero potential. From Fig. 3, it is visible that the region of the most negative electrostatic potential is spread over the O14, O15 atom of NO2 group and N4, N5 of the thiadiazole ring. This indicates the delocalization of π electrons over the nitro group and thiadiazole ring. This also reveals extended conjugation of the phenyl rings with the nitro group.
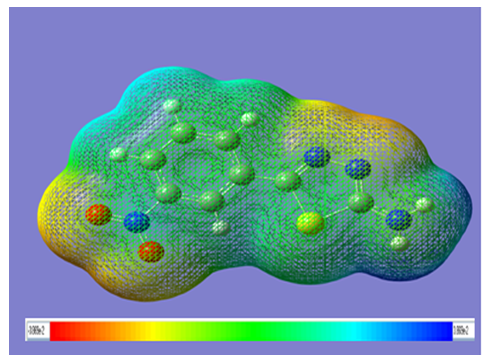 | Figure 3. Molecular electrostatic potential mapped on the isodensity surface for AMNT calculated at the B3LYP/6-311++G(d;p) level of theory |
3.5. HOMO-LUMO Analysis
- The highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) are the main orbitals that plays an important role in chemical stability [29]. The HOMO exhibits the ability to donate an electron and LUMO as an electron acceptor serves the ability to obtain an electron. The HOMO and LUMO energy calculated by B3LYP/6-311++G (d,p) level of theory show the energy gap which reflects the chemical activity of the molecule. HOMO energy (B3LYP) = −782.609 kJ/molLUMO energy (B3LYP) = −548.520 kJ/molHOMO − LUMO energy gap (B3LYP) = 234.089 kJ/molThe HOMO is positioned over the thiadiazole ring and amino group, the HOMO→LUMO transition implies an electron density transfer to Phenyl ring and nitro group from thiadiazole ring and amino group. This ICT between thiadiazole ring and Phenyl ring is responsible for existing biological activities. The atomic orbital compositions of the frontier molecular orbital are shown in Fig. 4.
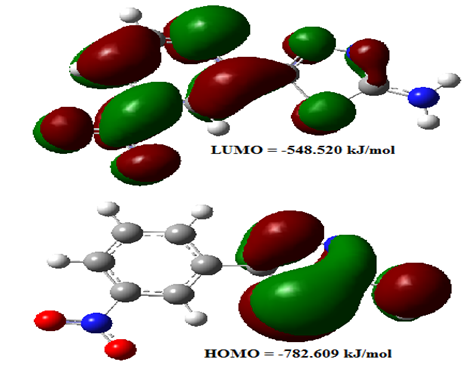 | Figure 4. The molecular orbitals of AMNT at B3LYP/6-311++ G(d;p) level |
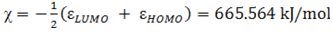 | (2) |
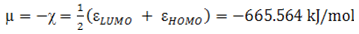 | (3) |
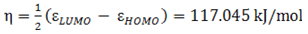 | (4) |
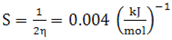 | (5) |
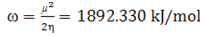 | (6) |
 | (7) |
3.6. Vibrational Spectral Analysis
- The vibrational spectra of 2-amino-5-(m-nitrophenyl) -1,3,4-thiadiazole molecule have been calculated by DFT with B3LYP functional having extended basis set 6-311G(d,p), 6-311+G(d,p), 6-311++G(d,p) and by HF with basis set 6-311++G(d,p) using Gaussian 09W package. Due to exclusion of anharmonicity, the calculated wave numbers are higher and therefore, scaled down by the wave number linear scaling procedure (WLS) [νobs/νcal = (1.0087 – 0.0000163 *νcal) cm-1] given by Yoshida et al. [22]. This molecule has 21 atoms, which gives 57 (3n-6) normal modes. AMNT has phenyl and thiadiazole rings with different functional groups namely nitro and amino respectively. Vibrational mode assignments have been made on the basis of relative intensities, line shape and potential energy distribution obtained from normal coordinate analysis. All the 57 fundamental vibrations of the free molecule are both IR and Raman active. The calculated vibrational wave-numbers and their PED for each normal mode are presented in Table 3. The calculated (scaled) infrared absorbance and Raman spectra are shown in Fig. 5 and Fig. 6, respectively.
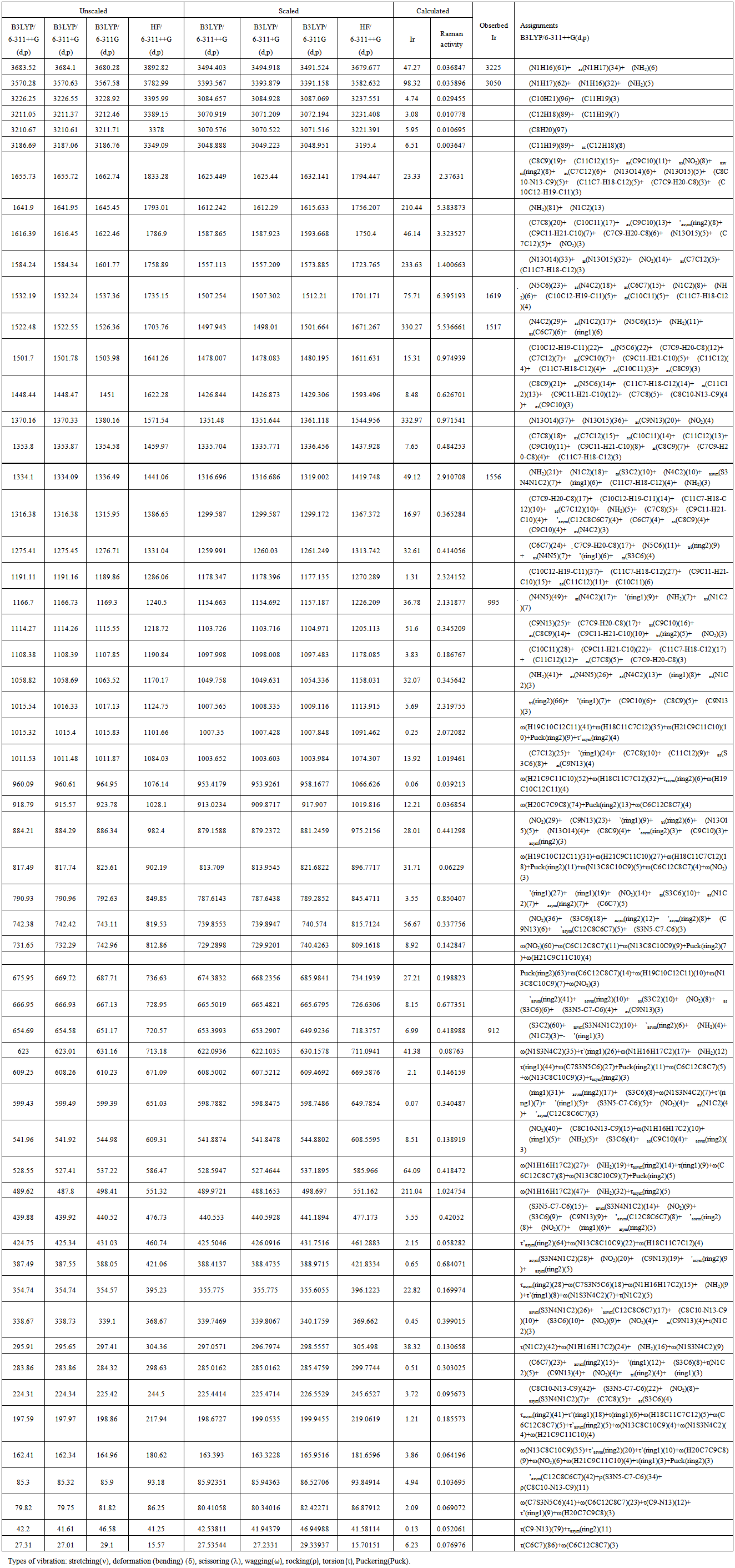 | Table 3. Potential Energy Distribution and vibrational wavenumbers of AMNT |
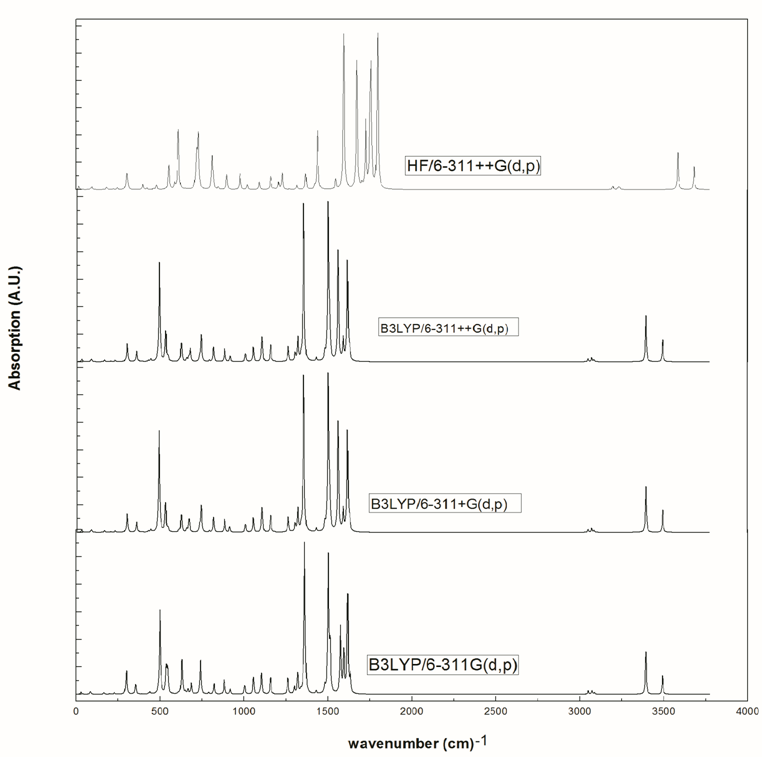 | Figure 5. Calculated infrared spectra of AMNT at various level of theory |
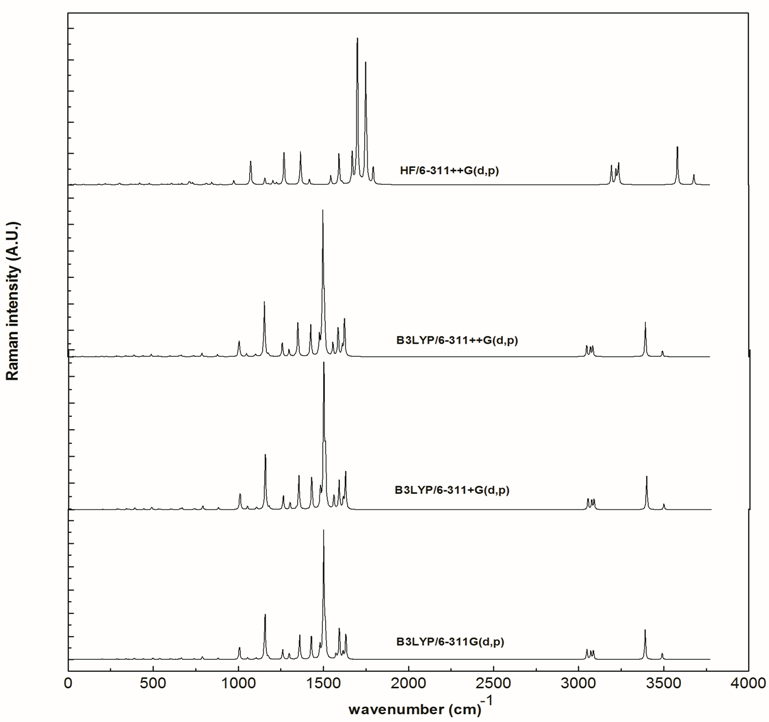 | Figure 6. Calculated Raman spectra of AMNT at various level of theory |
4. Conclusions
- Geometry of AMNT molecule was optimized using DFT at various levels of theory and also HF employing 6-311++G(d,p) basis set. The calculated values are also compared with experimental data. In general the structural parameters matches well with the experimental one, with few exceptions caused due to constraints imposed by isolated molecule model. Potential energy scan suggested one less stable conformer in which two rings are almost twisted by 180°. A detailed normal coordinate analysis of all the normal modes along with PED very clearly indicates the composition of each normal mode in terms of internal coordinates. Predictive IR and Raman spectra are very useful in the absence of experimental data. HOMO-LUMO, EPS and NBO may serve as a useful quantity to explain hydrogen bonding, reactivity and structure–activity relationship of molecules.
ACKNOWLEDGEMENTS
- Financial assistance to Mahesh Pal Singh Yadav from Jaypee University of Engg. & Technology, Guna is gratefully acknowledged.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML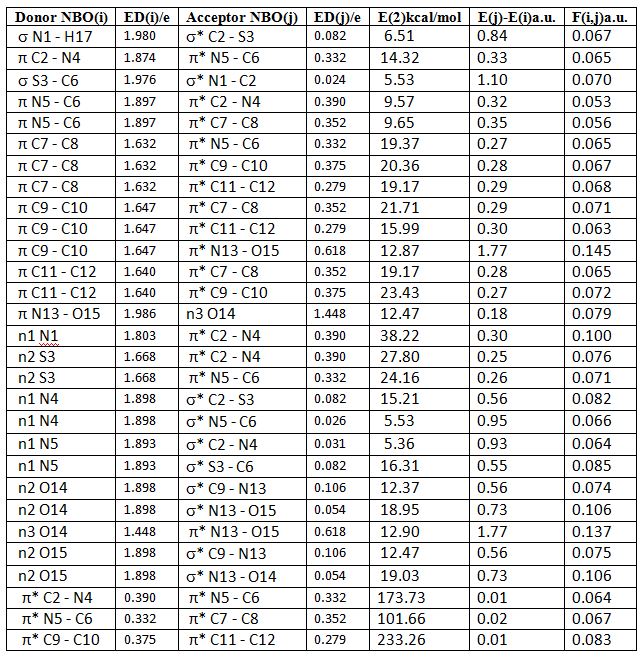
 O and improper blue-shifted C–H
O and improper blue-shifted C–H O hydrogen bonds, Phys. Chem. Chem. Phys., 6, 37-41.
O hydrogen bonds, Phys. Chem. Chem. Phys., 6, 37-41.