-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Materials and Chemistry
p-ISSN: 2166-5346 e-ISSN: 2166-5354
2012; 2(1): 10-15
doi: 10.5923/j.ijmc.20120201.02
Chemical Activities, a(H) and a(X), of Constituents in H2X Type Gas Molecules (X = O or S) at Arbitrary Degree of Dissociation
Nobumitsu Shohoji
LNEG - Laboratório Nacional de Energia e Geologia, LEN - Laboratório de Energia, Estrada do Paço do Lumiar, 22, 1649-038 Lisboa, Portugal
Correspondence to: Nobumitsu Shohoji , LNEG - Laboratório Nacional de Energia e Geologia, LEN - Laboratório de Energia, Estrada do Paço do Lumiar, 22, 1649-038 Lisboa, Portugal.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Chemical activities, a(X) and a(H), of constituents, X and H, in H2X type gas molecules (X = S or O) were evaluated as functions of temperature T and extent α of dissociation adapting a thermodynamic analysis procedure developed by Katsura for interpreting enhanced a(N) and a(H) in NH3 gas molecules with suppressed α by flowing. Present analysis results showed that both H2S and H2O gas molecules are chemically rather inert even at comparatively low α unlike nitrogen-family tri-hydrides XH3 that were proved to yield high chemical activity of each constituent in a state being away from thermodynamic equilibrium. The parameter α referring to the extent of dissociation of HnX type gas molecules appears to be a significant parameter in evaluating the chemical activities, a(X) and a(H), in the HnX gas molecules that are remained non-dissociated.
Keywords: Thermodynamics, Chemical activity, Dissociation, Non-equilibrium state, H2S, H2O
Article Outline
1. Introduction
- It is well known that N-rich nitride of metals might be synthesized at comparatively low temperature T under flow of gaseous NH3 of normal pressure. In pioneering works of this line of research published in 1930, Hägg[1] reported successful synthesis of mono-nitride for Mo and W and Lehrer[2] synthesis of Fe4N phase. Later in 1948, Jack[3] reported synthesis of Fe2N as well as Fe4N under flow of NH3 gas.Later, Katsura and collaborators[4] confirmed experimentally the validity of evidences reported by Hägg[1] demonstrating that, under flow of NH3 gas at normal pressure, mono-nitride MoN formed at 700ºC besides sub-nitride Mo2N but, when the processing temperature was risen by mere 25ºC to 725ºC, MoN decomposed to turn the reaction product to be consisted of Mo2N alone. Jehn and Ettmayer[5] reported that MoN synthesis was impossible in N2 gas environment even in autoclave that was capable of raising N2 gas pressure p(N2) up to 300 bar.Katsura[6] demonstrated that, for uranium sesqui-nitride U2N3+x (0 < x < 1) possessing extensive range of homogeneity composition synthesized at a given T, x tended to rise with the increasing NH3 gas flow rate (in other words, with the decreased extent α of dissociation of NH3). Later, Katsura and collaborators[7] demonstrated that N content in the Fe4N phase varied over the length 4 cm being dependent on the inevitable variation of the extent αof dissociation of NH3 along the flow path (i.e. decreasing a(N) on going from the upstream side to the downstream side of NH3 gas flow path on account of increasing α).During the course of surface nitriding experiment for tool steel block specimen, NH3 gas with suppressed extent α of dissociation was proved to function as hydriding medium at comparatively low T (probably lower than 300ºC) while it worked as nitriding medium with high nitrogen activity a(N) at higher T (probably higher than 400ºC)[8].Aiming at interpreting rationally all these available evidences regarding reaction of metals with NH3 gas with suppressed extent α of dissociation [1-8], Katsura [9] undertook thorough thermodynamic analysis to derive isothermal plots of chemical activity a(N) of N and chemical activity a(H) of H as a function of α for NH3. According to the analysis results presented by Katsura [9], a(N) as high as 104 might be gained with α = 0.2 or 103 with α = 0.5 at T = 700ºC while enhancement for a(H) realized by the suppressed α was modest compared with that for a(N).Later, Katsura and collaborators [10-12] systematically evaluated activity a(H) and a(X) for tri-hydride H3X of nitrogen-family elements X (= N, P or As) and demonstrated possibility of gaining very high a(X) and modestly enhanced a(H) through suppressed dissociation for H3X type gas molecules in general.In the present work, similar thermodynamic analysis was made for H2X type gas molecules (X = S or O) to evaluate isothermal plots of a(X) and a(H) as a function of α following formally the procedure developed by Katsura [9] for analysis of H3X gas molecules in state being away from dissociation equilibrium whereas, unlike H3X type nitrogen-family tri-hydride gas molecules, H2X gas molecules are highly resistant against spontaneous dissociation. Both H2S and H2O are known as corrosive molecular species (e.g., Ref.[13]) and thence their involvement in corrosion process is briefly considered with reference to the results of the present evaluation.
2. Thermodynamic Analysis Procedure
2.1. Characteristic features of HnX gas molecules
- As demonstrated by the available facts of corrosion cases[13], metallic materials might suffer from severe degradation in atmosphere containing H2O and H2S. For example, corrosion damages like SSCC (sulfide stress corrosion cracking) and HE (hydrogen embrittlement) are known to be induced in geothermal power plant and deep sour petroleum well rich in H2S as well as H2O. Thus, H2X gas molecules under consideration as well as H3X gas molecules (X = N, P or As) are certainly classified as corrosive chemical media.
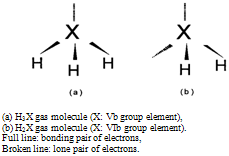 | Figure 1. Schematic "tetrahedral" configuration of electron pairs in sp3 hybrid orbital around |
|
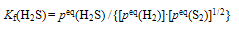 | (1) |
2.2. Analysis for H2S
- In case of H2S, dissociation reaction is represented by
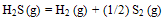 | (2) |
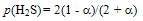 | (3) |
 | (4) |
 | (5) |
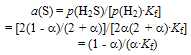 | (6) |
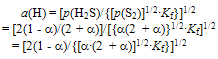 | (7) |
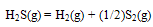 | (8) |
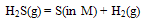 | (9) |
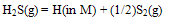 | (10) |
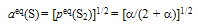 | (11) |
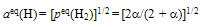 | (12) |
2.3. Analysis for H2O
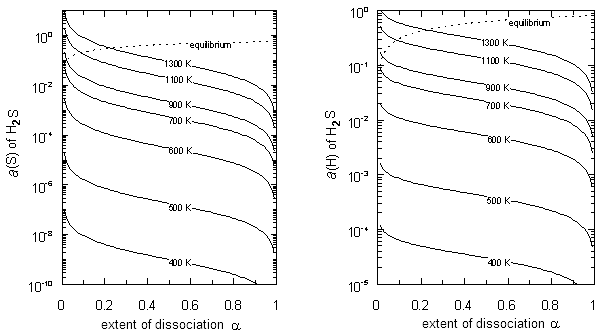
- Similar calculations were made for H2O and the results are plotted in Fig. 4. It is evident in Fig. 4 that a(O) vs. α and a(H) vs. α isotherms for H2O gas molecules at T = 1300 K are comparable to or lower than a(S) vs. α and a(H) vs. α isotherms for H2S gas molecules at T = 500 K. For H2O, aeq(O) and aeq(H) isotherms locate by far above the plots in Fig. 4 and thence they are not drawn in Fig. 4. It means that enhanced a(O) and a(H) cannot be gained for H2O gas molecules even at low α like for H2S and unlike for NH3. These evaluation results indicate that H2X type gas molecules (X = VIb group element) is not at all unstable unlike H3X type gas molecules (X = Vb group element) in spite of apparent similarity in electronic surrounding around X atom between the former and the latter as depicted in Fig. 1.
3. Discussion
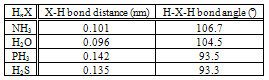
- According to molecular parameter values listed for HnX type gas molecules in Table 1, bonding strength between O and H in H2O must be by far stronger than that between N and H in NH3. This is not in contradiction to the present evaluation results for H2O suggesting low a(H) and a(O) even with suppressed α (Fig. 4) compared with very high a(N) and modestly enhanced a(H) for NH3 even at comparatively high α (Fig. 3). The similar arguments for NH3 and H2O appear to be valid for PH3 and H2S as well.As verified experimentally in the earlier works [6-8,10-12,17-20], where there are several species containing an element X coexisting in the reactants, X-containing chemical species possessing the highest a(X) in the reactants would determine the X content in the reaction product. For example, where amorphous carbon with a(C) > 1 is present in the reactant, C content in prepared carbide or carbonitride of metal would become higher than that under presence of graphite (reference state of C with a(C) = 1) alone [8,17-20] while N in NH3 gas molecule in a state being away from equilibrium state determined a(N) to yield N-rich reaction products that are not synthesized in N2 gas environment even at elevated pressure[1-12,17,18].Thus, O content in the reaction product prepared in gas phase containing H2O impurity as well as O2 impurity must be determined by chemical potential a(O) of O of H2O gas molecule represented by
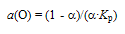 | (13) |
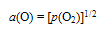 | (14) |
 | Figure 2. Chemical activity a(S) of S and a(H) of H in H2S plotted as a function of extent α of dissociation of H2S |
 | Figure 3. Chemical activity a(N) of N and a(H) of H in NH3 plotted as a function of extent α of dissociation of NH3 |
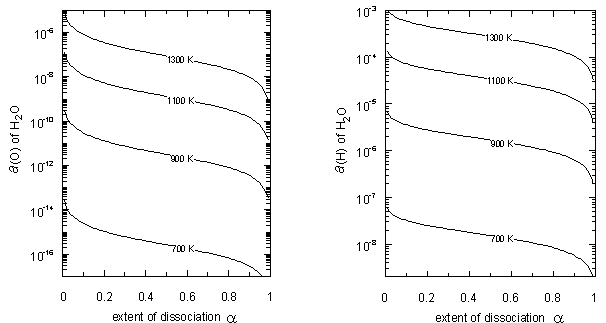 | Figure 4. Chemical activity a(O) of O and a(H) of H in H2O plotted as a function of extent α of dissociation of H2O |
- Nevertheless, chemical inertness of H2O gas molecule does not necessarily mean the electrochemical inertness of water in condensed state. Chemical reactivity and activity of condense water must be interpreted in terms of electrochemistry or solution chemistry rather than in terms of molecular chemistry. Under co-presence of H2S and H2O, yield of sulfuric acid H2SO4 is inevitable. Then, ionic species such as H+, SO42- and OH- in acidic solution would promote electrochemical process leading to corrosion. Chemical activity of element must be higher in form of ion than in form of neutral atom or molecule. As pointed out earlier in the text, the highest a(X) of the element X would determine the X content of the product in case that the element X exists in different forms in the reactant[6-12,17-20].
4. Conclusions
- Thermodynamic evaluation for chemical activities, a(X) and a(H), in H2X type gas molecules (X = S or O) was made as a function of extent α of dissociation of H2X gas molecules following formally the procedure developed by Katsura for evaluation of a(N) and a(H) in NH3 gas molecules with suppressed extent of dissociation[9] and for other XH3 type gas molecules (X = P or As)[10-12]. Although the H2X type gas molecules under consideration are resistant against spontaneous dissociation unlike the H3X type tri-hydrides of nitrogen-family element X and thence direct comparison for the evaluation results for dependence of a(X) and a(H) on α between H2X and H3X might not be fully justifiable, the present evaluation results look rational indicating that both H2S and H2O gas molecules are quite inert in chemical sense in contrast to high chemical activities of constituents, X and H, in H3X type nitrogen-family tri-hydrides under condition of suppressed dissociation.As such, the present thermodynamic evaluation results for stable H2X gas molecules together with the original analysis results for unstable H3X gas molecules presented by Katsura[9] appear to suggest that chemical activities, a(X) and a(H), of these HnX type gas molecules might be generally represented as functions of temperature T and extent α of dissociation.The aspect of controlling a(C) in metal carburizing reaction through arbitrary varying partial pressures of constituent gas species in gas mixture consisting of CO and CO2 or of CH4 and H2 was reported elsewhere[21-24] rather than through employment of amorphous carbon [8,18-20]. Thus, the evaluation results drawn in the present work for H2S and H2O demonstrating feasibility of determining the activities, a(S), a(O) and a(H), as functions of T and α must be considered valid and realistic.For the inherently unstable gaseous molecular species, low α might be realized by simply arranging experimental setup with gas flow system to retard dissociation of the gas species. On the other hand, to realize low α condition for stable gas species H2X (X = S or O), admixing with excess H2 to gain high a(H) or admixing with X to gain high a(X) might be desirable.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML