-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Internet of Things
2017; 6(3): 98-105
doi:10.5923/j.ijit.20170603.02

Performance Evaluation of Buffer Size for Access Networks in First Generation Optical Networks
Baruch Mulenga Bwalya, Simon Tembo
Department of Electrical and Electronic Engineering, University of Zambia, Lusaka, Zambia
Correspondence to: Baruch Mulenga Bwalya, Department of Electrical and Electronic Engineering, University of Zambia, Lusaka, Zambia.
| Email: |  |
Copyright © 2017 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Enhancing network performance and reducing energy consumption by the routers are two very important design challenges faced by router manufacturers today. Routers require buffers to hold packets in times of delay. Therefore, buffer size plays a big role in router design. Network performance and router energy consumption is determined by the technologies employed to build the routers. Manufacturers use the rule of thumb to assign network buffer to routers, which increases buffer size linearly with an increase in network capacity. This results in large buffers that require a lot of power and board space, and are a challenge to router manufactures. In this paper, we use OPNET simulations to study buffer size in access networks, independent of network capacity, to come up with an optimal buffer size for the network. We propose and use a model to illustrate buffer size that is optimal for access networks. By having a buffer size that can hold at least fourteen packets, we illustrate that this results in reduced power consumption by the router and enhanced network performance.
Keywords: Internetworking, Transmission Control Protocol, Buffer Size, Datagram Forwarding Rate
Cite this paper: Baruch Mulenga Bwalya, Simon Tembo, Performance Evaluation of Buffer Size for Access Networks in First Generation Optical Networks, International Journal of Internet of Things, Vol. 6 No. 3, 2017, pp. 98-105. doi: 10.5923/j.ijit.20170603.02.
Article Outline
1. Introduction
- All routers require buffers to store packets during times of delay in the network. The buffers should ideally be large enough to accommodate packets that are in queue but fast enough not to hold packets in queue longer than necessary. They should also be small enough to use fast memory technologies such as static random access memory (SRAM) or all-optical buffering [1, 20]. In an electrical packet-switched network, packet contention at the routers is resolved with a store and forward technique, where packets are stored in a buffer, and are sent out when random access memory (RAM) allows. The size and speed of electronic RAM are still bottlenecks as router manufacturers still use large, slow, off-chip dynamic random access memory (DRAM) chips, to satisfy large buffer requirements. Large buffers lead to large boards which are too hot and consume a lot of power. All-optical buffering currently does not have an equivalent to electronic RAM, so optical packet switches adopt a different approach to congestion control in the network [2, 9, 19]. While all-optical packet switching is regarded as a long term solution to increasing data rates in optical telecommunication networks, this has not yet been fully realized due to a number of factors; one of which is the problem of contention resolution during times of congestion because of the extremely long lengths of fibre required to buffer several packets for various time delays when using fibre delay lines (FDL) [3]. However, optical packet switching has advanced from just using long lines of fibre to buffer packets, to include a switching fabric for switching packets optically. This kind of switching has lower power consumption and takes up less board space compared to electronic RAM and FDL. Shinya et al. [5] demonstrated a photonic crystal based all-optical bit memory operating at very low power, where each photonic cell could only buffer a single bit, with all wavelengths sharing the same buffer space, just like in electronic buffering. Such low buffer capacities make it difficult to buffer packets in a network that has an optical switching fabric with high data transmission rates [6].Optical networks can be identified as first or second generation networks. First generation networks are point-to-point networks which use fibre as a faster substitute for copper cables. Wavelength Division Multiplexing (WDM) technology extended these systems to have more than one wavelength per fibre, thereby, increasing their capacity several times over. At each switching point in such networks, all wavelengths are terminated and converted to electrical form, and are remodulated onto the optical carrier at the output. Second generation networks obviate the need for conversion to the electronic domain by providing switching and routing services at the optical layer. Such networks are known as all optical networks [4].Further to advances with WDM technology, dense wavelength division multiplexing (DWDM) has made it possible for networks to achieve ultra-high data transmission rates [6]. The role of optics in our study is to illustrate that with increasing data rates, calculations for buffer size must be made, independent of the capacity of the transmission links in the network.In this paper, we simulate a first generation optical network, set in a multipath environment, using OPNET simulation software, although now known as Riverbed Academic Modeller, we will refer to it as OPNET in the rest of this paper. Multipath routing has the potential of improving the throughput of traffic in the network but requires optimum buffers in the access network, as it is only available in the core of the network. The main disadvantage associated with multipath routing manifests as packet disordering at the receiver, since traffic is split into these multiple paths with different latencies creating jitter [16]. Solutions to these issues have been proposed in [17] and [18]. The rest of the paper is organized as follows. In section 2, we give an overview of buffer sizes and in section 3 we address buffer size and power consumption. In section 4, we look at simulation set up. Section 5 presents simulation results and discussion. We conclude the paper in section 6.
2. Overview of Buffer Sizes
- Various proposals for calculation of buffer size have been made throughout the years. Here, we present some of the proposals made, to address the problem of buffer size in networks.
2.1. Bandwidth Delay Product
- Bandwidth delay product or the rule-of-thumb gives a measure of required buffer size for a particular network based on its average round trip time and link capacity. The rule-of-thumb comes from a desire to keep the bottleneck link as busy as possible, so that the throughput of the network is maximized by providing a buffer size equal to the bandwidth delay product. This buffer size prevents the link from going idle and thereby losing throughput. However, Transmission Control Protocol (TCP) “sawtooth” congestion control algorithm is designed to fill any buffer, and deliberately causes occasional packet loss so as to provide feedback to the sender. Therefore, no matter how big we make the buffers at a bottleneck link, TCP will cause the buffer to overflow [19].The bandwidth delay product, which is widely used in determining buffer size states that each link needs a buffer size:
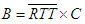 | (1) |
2.2. A Case for Small Buffers
- The rule-of-thumb complicates router buffer design due to the buffer sizes that can be required when the network capacity is large. For example, a 10Gbits/s router linecard needs approximately 250ms x 10Gbits/s = 2.5Gbits of buffer. The amount of buffer required for a router will grow linearly with linerate. Appenzeller et al. [9] conclude that buffers in backbone routers which use the rule-of-thumb, are much larger than they need to be, possibly by two orders of magnitude. They argue that the rule-of-thumb is now outdated and incorrect for backbone routers because of the large number of flows multiplexed together on a single backbone link. They go on to propose that a link with N flows requires no more than:
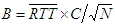 | (2) |
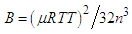 | (3) |
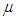 is the link capacity, RTT is the round trip time and n is the number of TCP connections. In [10], the problem of router buffer size is formulated as a multi-criteria optimization problem. The solution to this problem provides further evidence that buffer size should be reduced in the presence of traffic aggregation. The study concludes that the minimum required buffer is smaller than what previous studies suggested.Enachescu et al. [1], conducted a study on buffer sizes for backbone routers. Building on the work of Appenzeller et al. for the case of small buffers, Enachescu et al. explore how buffers in backbone routers can be significantly reduced even more, to as little as a few dozen packets, if we are willing to sacrifice a small amount of link capacity. They [1] argue that if the TCP sources are not overly bursty, then fewer than twenty packets buffers are sufficient for high throughput. This network of tiny buffers can have buffer size of:
is the link capacity, RTT is the round trip time and n is the number of TCP connections. In [10], the problem of router buffer size is formulated as a multi-criteria optimization problem. The solution to this problem provides further evidence that buffer size should be reduced in the presence of traffic aggregation. The study concludes that the minimum required buffer is smaller than what previous studies suggested.Enachescu et al. [1], conducted a study on buffer sizes for backbone routers. Building on the work of Appenzeller et al. for the case of small buffers, Enachescu et al. explore how buffers in backbone routers can be significantly reduced even more, to as little as a few dozen packets, if we are willing to sacrifice a small amount of link capacity. They [1] argue that if the TCP sources are not overly bursty, then fewer than twenty packets buffers are sufficient for high throughput. This network of tiny buffers can have buffer size of: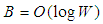 | (4) |
2.3. A Case for Large Buffers
- Dhamdhere and Dovrolis [22] raise some concerns about previous recommendations on small buffers in the network. They show that small buffers can lead to excessively high packet loss rates in congested access links that carry many flows. They argue that even if the link is fully utilized, small buffers lead to lower throughput for most large TCP flows.In [22], they state that when using small buffers, there is packet loss rate of up to 15% in congested access links that carry many flows. Such frequent packet losses can negatively affect certain applications, making application layer performance less predictable. The study recommends an increase in buffer sizes to improve network performance.Avrachenkov et al. in [11] studied the effect of the Internet Protocol (IP) router buffer size on the sending rate, the goodput and the latency of a TCP connection. They analysed short TCP transfers as well as persistent TCP connections. In [11], they conclude that small buffers increase packet loss resulting in a poor sending rate and goodput. In the case of large buffers, the queuing delays and round trip times cause a poor sending rate and goodput. Therefore, for a given TCP connection, there must be an optimal value of the buffer size for the bottleneck IP router, which must be different for each TCP connection due to propagation delays. They note several reasons for the buffer size to be increased, as opposed to being reduced. They suggest that for a system to be robust, buffers must be set larger, rather than smaller.
2.4. A Case for an Optimal Buffer
- From the foregoing reviews, it is clear there is no one agreement on what the buffer size should be. Gorinsky et al. [12] attempted to reconcile the different approaches by arguing that the problem of buffer sizing needs a new approach other than the traditional bandwidth delay product; over-square-root or small buffer rule; and connection-proportional allocation, which support increased buffer size. The suggestion in [12] is for a new formulation to address the problem of buffer size by designing a buffer sizing algorithm that accommodates the needs of all Internet applications; that does not involve the routers in any additional signalling. This, they argue, keeps the network queues short by setting the buffer size to 2L datagrams, where L is the number of input links. To find an optimal buffer size for a network carrying both TCP and User Datagram Protocol (UDP) traffic, Vinoth and Thiruchelvi [13] proposed an equation:
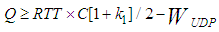 | (5) |
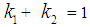 and
and 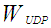 is the total number of UDP packets. However, we note in [10] that UDP does not use any congestion control and reliable retransmission and it is mostly employed for delay sensitive applications such as Internet telephony. UDP traffic does not contribute much in terms of the load in IP networks.
is the total number of UDP packets. However, we note in [10] that UDP does not use any congestion control and reliable retransmission and it is mostly employed for delay sensitive applications such as Internet telephony. UDP traffic does not contribute much in terms of the load in IP networks. 3. Buffer Size and Power Consumption
- Router design has a significant impact on the cost of the router, power consumption and the cost of memory. Small buffers can significantly reduce power consumption, the amount of fast memory required to build the buffer of the router and size of the buffer; thereby reducing the cost of the router. Small buffers also have the advantage of reducing queuing delays, while maintaining full link utilization at the target link; a design that comes with the cost of high loss rate of packets [14].To compare power utilization of an optical router with a traditional electronic router, Gu et al. [15] designed an optical router and an electronic router to deliver the same maximum throughput. They used a moderate 12.5Gbit/s for each port on the routers. The electronic router was simulated in Cadence Spectre. The simulation results show that for the electronic router, on average, the crossbar consumes 0.07pJ/bit, the input buffer consumes 0.003pJ/bit and the control unit consumes 1pJ to make decisions for each packet. The optical routers implemented the same routing algorithm and had no input buffers. This made the optical buffers under study consume one or two orders of magnitude lower power than the electronic routers. A particular Cygnus only consumed 3.8% power of the high performance electronic router while routing 512 bit packets.
4. Simulations
- We use OPNET to set up a network to evaluate buffer size. The network is simulated with Abilene backbone network, where low and heavy traffic scenarios are routed through the network. The objectives of the simulation are to find an optimal buffer size for the network with minimal packet loss, independent of link capacity, due to an increase in data transmission rates. The links of the future are projected to be higher and it is improbable that such links will be utilized one hundred percent during data transmission. Packets must, therefore, spend as little time as possible at the routers by switching faster with small buffers.
4.1. Network Setup
- The network simulation was setup with Abilene backbone network [21], shown in Figure 1, as a first generation optical network, using OC-192 links, which have a capacity of well over 9 Gbps. This setup is in a multipath environment, where packets can take the shortest available route. A server was placed on the Seattle side of the network, as shown in Figure 2, and all client or host machines were placed on the New York side of the network, as shown in Figure 3. The server and hosts were set up to have direct connection to the access routers. Throughout the simulations, network hosts were varied from six to forty-eight, directly connecting to an access router.
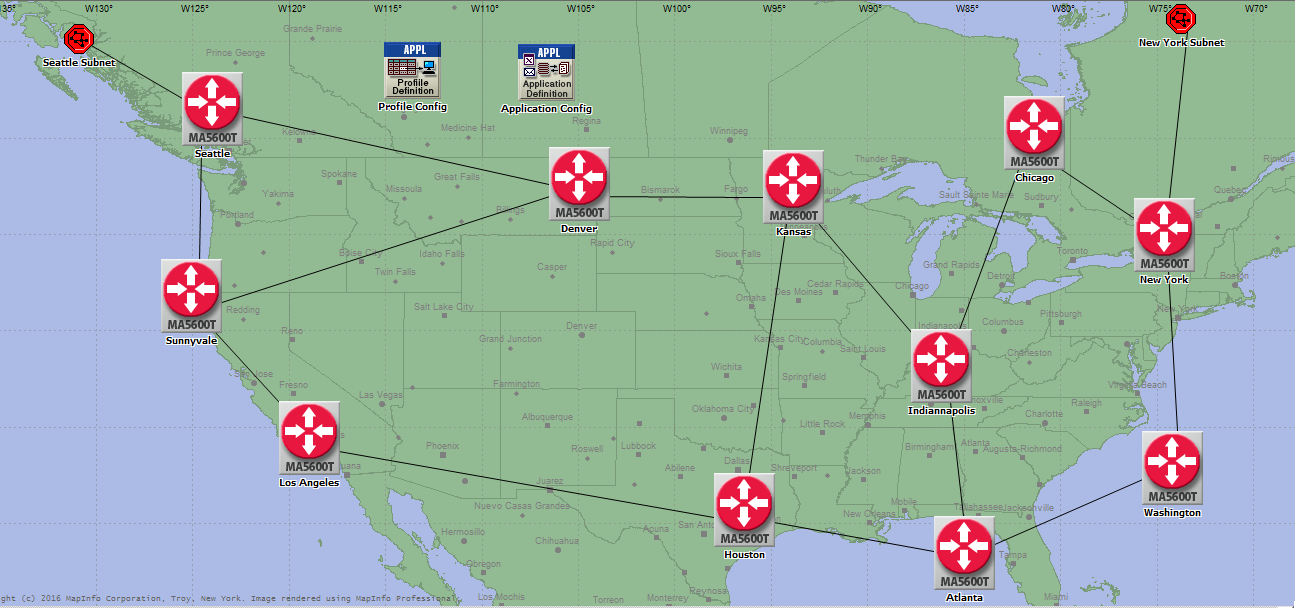 | Figure 1. Abilene backbone network [21] |
 | Figure 2. Server side setup at Seattle |
 | Figure 3. Host setup for New York subnet with six host connections to an access router |
|
|
5. Simulation Results and Discussion
- The objective of our simulation was to find an optimal buffer size. The focus of our study is not on link utilization or its relationship to buffer size.
5.1. Packet Drops across the Network
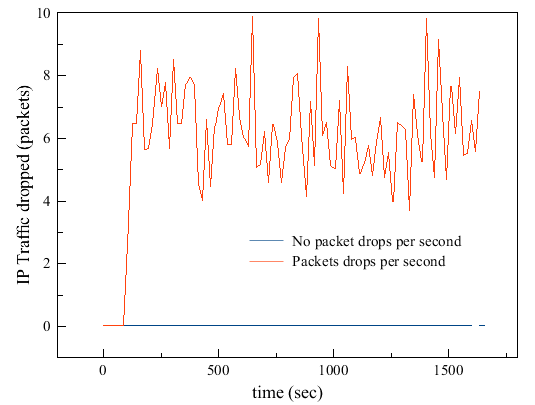
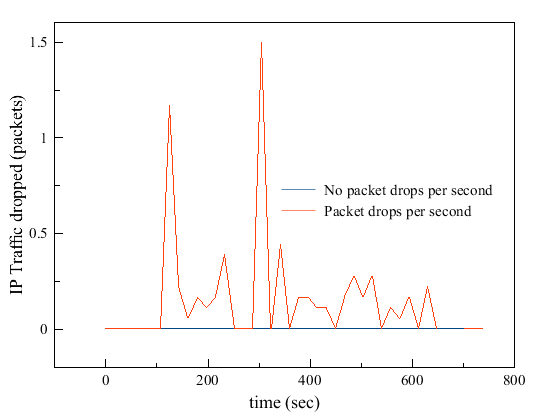
- Packet drops were observed when the buffer size and datagram forwarding rates were not sufficient for traffic routing. This was observed both in low and high traffic scenarios as shown in Figure 4 and Figure 5. With such an observation, the buffer size was adjusted further to find an optimal buffer size.Figure 4 shows packet drops in a low traffic environment with buffer size set at 17975 bytes and datagram forwarding rate (DFR) at 300 packets per second. Figure 5 shows packet drops in a high traffic environment with buffer size set at 40975 bytes and DFR set at 300 packets per second. With these settings, we observed packet drops at the edges of the network with one server and six hosts.
 | Figure 4. IP traffic flow in low traffic environment |
 | Figure 5. IP traffic flow in high traffic environment |
5.2. No Packet Drops across the Network
- By simulation, we adjusted the buffer size until we found values for buffer size and DFR where packets were not dropping. This occurred at buffer size 17975 bytes and DFR of 390 packets per second for the low traffic environment as shown in Figure 4. For a high traffic environment, we set buffer size at 40975 bytes and DFR at 16000 packets per second as shown in Figure 5. Theoretically, this means that all packets are being delivered across the network with no packet drops. This scenario also means that the buffer size is optimal and sufficient for packet transfers.As we varied the buffer size alone, while keeping DFR constant, we found the minimum buffer size required where no packets could drop across the network. From the point of the minimum buffer size, we adjusted the DFR downwards, to find the minimum forwarding rate at which no packets were dropping across the network for buffer size we had set. Minimums for a pair of datagram forwarding rate and buffer size were noted. Next, we adjusted both the DFR and the buffer size and we discovered that doing so causes excessive packet loss. We then increased one value and reduced the other. As we increased the buffer size, we reduced the DFR. This is what we state as an inverse relationship between the buffer size and DFR. We have depicted this relationship by graphing buffer size against DFR as shown in Figure 6 and Figure 7. Though we might not have found the accurate points or values for this relationship, we are satisfied that when buffer size is increased and DFR is reduced, a minimum value is found at which both these values can sustain network routing with minimal or no packets dropping across the network. We did this for low and high traffic scenarios in the network.
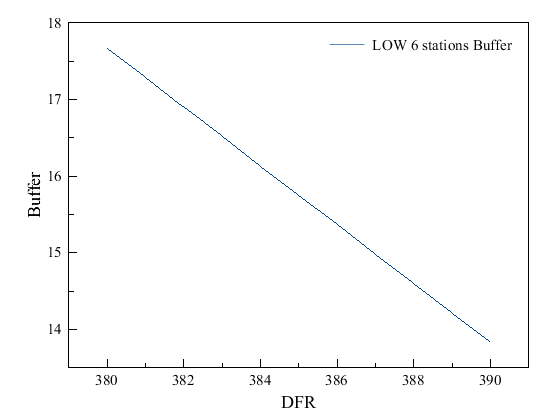 | Figure 6. Buffer size plotted against datagram forwarding rate adjusted at intervals in low traffic environment |
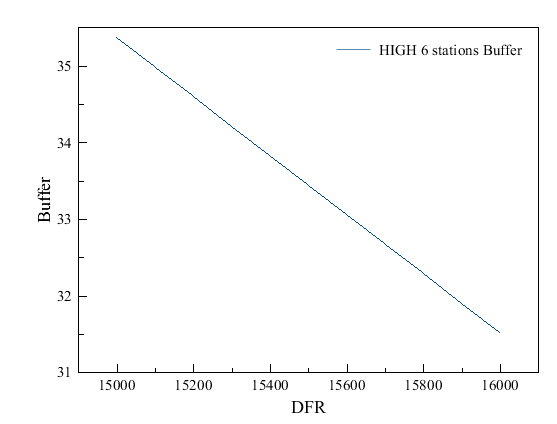 | Figure 7. Buffer size plotted against datagram forwarding rate adjusted at intervals in high traffic environment |
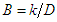 | (6) |
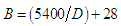 | (7) |
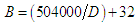 | (8) |
5.3. Discussion
- This paper summarizes a study of the feasibility of small buffers in first generation optical networks. With increasing link capacities, especially optical links, buffer sizes will increase linearly if the bandwidth delay product is used to come up with buffer sizes. Large buffers are not ideal for fast networks as they add to the delay of packets being routed. In this study, we have observed that a network can reach a point where no packets are dropped and all packets are delivered between the two end-points of the network. The absence of packet drops theoretically means that buffer size is optimal and packets deliveries and acknowledgments are happening in the network without any need for TCP to drop packets in its transmission. Buffer size and DFR were set to the same value all across the network, while adjusting the number of hosts on the client side of the network for both the low and high traffic environments. We noted that for the low traffic environment, packets were dropped when we increased the number of hosts to twenty-four. This prompted us to double the buffer size at the edge of the network, which is the New York local router; which had direct connection to the network hosts on the client side. This meant that the buffer size for traffic in low traffic environment needed to be doubled when more than twenty-four ports were being used at the router. This was not the case for high load traffic. The optimal buffer size, for both low and high traffic environment can, therefore, be calculated from equation (8), which we present as the main equation from our study. Thus:
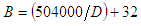 The formula we present from our study reduces the buffer size significantly from the traditional bandwidth delay product. This, in turn, reduces power consumption and board space when building the routers. The result is smaller, power efficient routers; which enhance network performance on networks with high link capacities.In our simulations with OPNET, we used 100Gbps Ethernet duplex link on the access network. The core of the network used OC-192. The RTT was observed at 0.055s, which was the highest RTT from our simulations. With these values, we can calculate the buffer size that would be required for our router using the bandwidth delay product and come up with a buffer size of 5.5GB. Contrast this value with the buffer size we get from our simulation, which is 40975 bytes or simply 50KB in high traffic scenario. A router with 5.5GB of buffer will require a lot of power and board space, resulting in a large router, that will hold packets longer during times of delay as it will queue up more packets compared to a router that has less buffer. A router with 50KB of buffer will require less power to run, take up less board space, compared to a router with 5.5GB of buffer. A 50KB router will hold fewer packets in times of delay, compared to a large buffer of, say, 5.5GB. This makes the smaller router more efficient by utilizing less power and holding packets for a shorter time in comparison to a large buffer. The result is enhanced network performance.We also noted in our simulations with OPNET that we could only simulate not more than 50,000,000 events. This gave us the difference in simulation times we observed in Figure 4 and Figure 5, even though the simulation time was set as the same in both scenarios. This did not affect our results in any negative way except that the time of simulation is shorter as more events or data is flowing during the simulation.
The formula we present from our study reduces the buffer size significantly from the traditional bandwidth delay product. This, in turn, reduces power consumption and board space when building the routers. The result is smaller, power efficient routers; which enhance network performance on networks with high link capacities.In our simulations with OPNET, we used 100Gbps Ethernet duplex link on the access network. The core of the network used OC-192. The RTT was observed at 0.055s, which was the highest RTT from our simulations. With these values, we can calculate the buffer size that would be required for our router using the bandwidth delay product and come up with a buffer size of 5.5GB. Contrast this value with the buffer size we get from our simulation, which is 40975 bytes or simply 50KB in high traffic scenario. A router with 5.5GB of buffer will require a lot of power and board space, resulting in a large router, that will hold packets longer during times of delay as it will queue up more packets compared to a router that has less buffer. A router with 50KB of buffer will require less power to run, take up less board space, compared to a router with 5.5GB of buffer. A 50KB router will hold fewer packets in times of delay, compared to a large buffer of, say, 5.5GB. This makes the smaller router more efficient by utilizing less power and holding packets for a shorter time in comparison to a large buffer. The result is enhanced network performance.We also noted in our simulations with OPNET that we could only simulate not more than 50,000,000 events. This gave us the difference in simulation times we observed in Figure 4 and Figure 5, even though the simulation time was set as the same in both scenarios. This did not affect our results in any negative way except that the time of simulation is shorter as more events or data is flowing during the simulation.6. Conclusions
- As link capacity is increasing with improvements in optical technology, buffer size calculated from the rule of thumb increases linearly. This in turn increases router power consumption and board space due to the routers increased size. We have also noted that multipath routing in the core of the network reduces the load in the core of the network, leading to the possibility of employing small buffers in the core of the network. Such buffers can be as small as 7 packets.Small buffers improve network performance. Consequently, we propose the equation as an alternative to big buffers, where D is the DFR and is non-zero.Our proposed equation will make access networks more efficient, use less power and reduce the router size. Small buffers are ideal for networks with fast links like a first generation optical network. Our further work will involve developing an interface on a router where network administrators can set buffer size and DFR based on their networking needs and also trying our proposed model on a real world network.
ACKNOWLEDGEMENTS
- I wish to acknowledge Dr. S. Tembo, Dr. M. Sumbwanyambe and Dr. D. Banda for the valuable guidance.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML