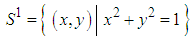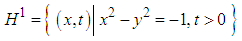-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Internet of Things
2016; 5(1): 17-28
doi:10.5923/j.ijit.20160501.03

A Geometric Structure for Internet of Things Indexing
Telesphore Tiendrebeogo1, Oumarou Sié2
1Department of Mathematics and Computer Science, Polytechnic University of Bobo Dioulasso, Bobo Dioulasso, Burkina Faso
2Department of Computer Science, University of Ouagadougou, Ouagadougou, Burkina Faso
Correspondence to: Telesphore Tiendrebeogo, Department of Mathematics and Computer Science, Polytechnic University of Bobo Dioulasso, Bobo Dioulasso, Burkina Faso.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

As the number of wireless devices increases and their size becomes smaller, there can be more interaction between everyday objects of our life. The proliferation of these devices in a communicating-actuating network creates the Internet of Things (IoT). We currently attend the deployment of a new generation of interconnected objects equipped with capacities of communication, detection and activation (wireless transport networks of information, RFID (Radio Frequency Identification System), WSAN (Wireless Sensor and Actuator Network), etc) for many applications. Thus, the interconnection of objects equipped with advanced capacities of treatment will lead to a revolution in term of creation and availability of service and deeply will change our way of interacting with our environment. In short, we attend an increasing mixture between the physical world and the virtual world. This paper presents a vision of cloud centric for worldwide implementation of Internet of Things. We propose a structure of tree hyperbolic, using the properties of the hyperbolic geometry and which allows the interconnection then the indexation of the various objects associated with this standard system. These mechanisms are based on greedy routing algorithm in the Poincaré disk model. We show how this virtualization of the objects in our structure which is not other than a Distributed Hash Table (DHT), allows to make scalable, reliable and resisting the communication between the entities even in a dynamic context of networks.
Keywords: Internet of Thing, DHT, Hyperbolic Tree, Indexing, Poincaré Disk, Greedy Routing, Routing by holes bypass
Cite this paper: Telesphore Tiendrebeogo, Oumarou Sié, A Geometric Structure for Internet of Things Indexing, International Journal of Internet of Things, Vol. 5 No. 1, 2016, pp. 17-28. doi: 10.5923/j.ijit.20160501.03.
Article Outline
1. Introduction
- The internet of things [1] refers to the only addressable objects and their virtual representations in a structure similar to the Internet. Such objects can be bound with information on them, or can transmit data of real time sensor of their state or other useful properties associated with the object. RFID Technology [2-4] sees generally as a key activator of Internet of things, because of its capacity to track a large number of only recognizable objects with the use of Electronic Product Code (EPC). However, other sorts of omnipresent devices of sensor, bar codes, or 2D codes can be also used to allow Internet of Things (IoT). The vision of the Internet inclusion of the things of simple more complex and more intelligent, objects of communication, involves to implement multi-field approach of new technologies, concepts and models (Development of integrated circuits, management of energy, systems and principles of communication, incorporated systems and packaging, acquisition and data processing, experiment on the ground) and supposes to take of many scientists, commercial and challenges of techniques. Besides, a radical evolution of current Internet in a Network of the connected objects which collects not only information of the environment and interacts with the physical world (the activation/command/control), but also uses existing standards of Internet to supply services for the transfer of the information, the analytics, the applications and the communications. Fuelled by the frequency of devices allowed by the wireless technology opened as Bluetooth, RFID, services of WiFi and phone data as well as the incorporated sensor and actuator nodes, IoT went out of its early childhood and is about to transform current static Internet in Future completely integrated Internet [5]. Internet revolution led to the interconnection between people on an unprecedented scale and to the speed. The following revolution will be the interconnection between objects and the creation of an intelligent environment. Only in 2011, the number of devices connected on the planet caught up the real number of people living there. At present there is 9 billion connected devices and we wait in the fact that it reaches 32 billion devices before 2020 [6].Figure 1 presents architecture of the Internet of things.
 | Figure 1. Internet of Things Schematic showing the end users and application areas based on data |
2. Related Work
- The discovery of Virtual Entities and the Services IoT is an essential aspect of Internet of Things. Contrary in small-scale silos of application making up an Intranet of Things, the applications and the services cannot be configured as regards fixed set services. At first, this is due to the underlying dynamics of the system IoT resulting from the mobility of physical entities and devices IoT, as well as the changeable availability of services because of the constraints of the underlying resources and from devices. Secondly, new sorts of applications and the services can be allowed, if the application can be written for a generic scenario, for example, an intelligent environment of the city, which should then work the same way to Berlin and Madrid without vast configurations.The proposed approach [7] is based on the creation and the preservation of a topology of cover which connects logically all the participating nodes/objects in the physical network (see Figure 2). Any node which connects to the physical network has to join the virtual infrastructure. In the virtual infrastructure, multiple networks of cover can be created with everything or a subset of the nodes of network. During the initiating of the physical network, the connected devices must be able to become identified. On the establishment of connectivity and the capacity of communication of multi-hop among participant’s nodes, overlay networks must be formulated. Overlay networks can summarize the topology of physical network and hide any details of the underlying physical infrastructure, bind for example the establishment or torn downward, from failures of node, the mobility of node, etc. Given the existence of an overlay network, participating in nodes has to store and retrieve data using a protocol P2P. Information retrieval can be realized with the storage and the recovery of pairs of key value. Every node which wishes to store a pair, of key-value, or to question a value based on a key, can realize it by using a DHT that operates on-top of the overlay topology. In a similar way, several applications can be built taking under consideration the existence of a high level Generic Application Programming Interface (API) that will provide them access to distributed (or centralized) repositories of data. Specific functions, as put (key, value) and get (key), can be displayed for the interaction of licence with a protocol DHT which works over a non-reliable IoT environment.
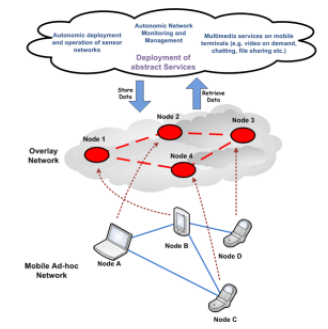 | Figure 2. Proposed approach for autonomic and decentralized services in the IoT |
3. Hyperbolic Geometry
- In this section, we interest particularly in the various elements allowing to define the hyperbolic structure of the geometry which we use in our model. Indeed, we focus on the notion of points, lines and circles who allow to characterize the metrics us concerning. One of the properties which characterizes the hyperbolic geometry is the fact that the Euclide's fifth postulate is not anymore true [18] [19].
3.1. Notion of Hyperbolic Line and Unit Circle
- We try to present briefly the notion of line in the hyperbolic plan together with the notion of unit circle represented in the spherical geometry. We present as follows these concepts:
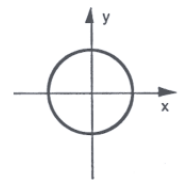
3.1.1. The Unit Circle (Represented in Figure 3)
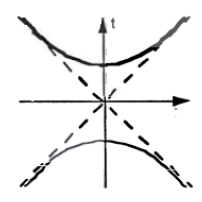
3.1.2. The hyperbolic Line (Represented in Figure 4)
3.2. Metric of Hyperbolic Distance and Computing Principle
- Given two pairs of points of the hyperbolic plan how to compare their distances? To do it, it is necessary to calculate individually their distances before comparing the obtained values. From a theoretical point of view, we could by means of a rule connect the points two-two before comparing them. But this link between points has to suit to the group of geometrical transformation of the hyperbolic context. So, so that it is for the case of the line or the circle, we choose the group of hyperbolic transformation which suits us. Our point of view concerning the comparison of two line segments is illustrated by the following principle.Principle of Superposition: Two line segments have the same length if and only if they can be superimposed by an element of the group of geometrical transformations.These positive transformations [20] have as well the property as there is a unique (positive) transformation which takes into account one suggestion to another one. Indeed, we can use our principle of superimposing by returning all our segments of line managed in a fixed canonical position, which we call Paris, to compare lengths. For a while, Paris had kept a metrics fixed length which was used for the comparison all over the world. So there is a unique positive geometrical transformation which takes into account one suggestion in Paris. Otherwise, we can think in Paris being transformed in a given point
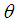 By a positive transformation
By a positive transformation 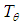 . We present
. We present 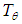 explicitly and define Paris.1) The circle Let Paris =
explicitly and define Paris.1) The circle Let Paris = 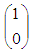 Then
Then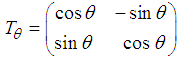 | (3) |
 on
on 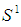 is identified with
is identified with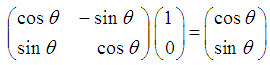 | (4) |
 Then
Then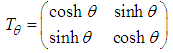 | (5) |
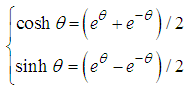 | (6) |
 on
on  is defined with
is defined with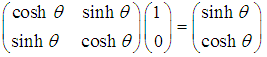 | (7) |
3.3. The Poincaré Disk Model Presentation
- The model of Klein of the hyperbolic plan shows that the hyperbolic lines are "straight", but we could also consider other properties. We describe here a model, in plan H. Poincaré, which is another another equivalent description of the hyperbolic plan, but he has the interesting property which is that the hyperbolic circles are Euclidian circles. For the Klein-Beltrami model we used central projection of
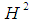 into the plane t = 1. Remind that for the sphere stereographic projection took circles to circles. We can apply the same idea for
into the plane t = 1. Remind that for the sphere stereographic projection took circles to circles. We can apply the same idea for 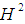 in our Minkowski geometry [21]. A natural place to choose from the projection point is the antipode of Paris, namely
in our Minkowski geometry [21]. A natural place to choose from the projection point is the antipode of Paris, namely
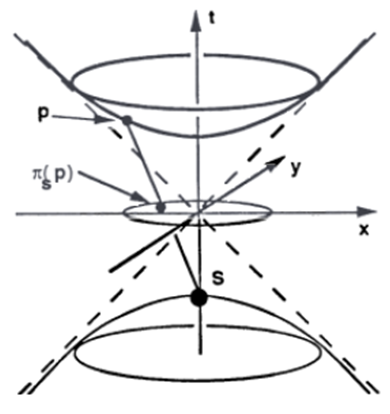 | Figure 5. The Klein model |
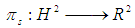 Besides, the image of
Besides, the image of 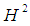 under
under 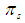 is the unit disk again, but in the plane t = 0. But what represents the image of a hyperbolic line? One easily to notice that it is about circles situated in the unit disk and which are orthogonal on the border of the disk in question or are associated to diameters in the latter. Poincaré disk model possesses an important property which is that the angular gap between two circles images of two lines is the same measure that the angle describes by two lines in the hyperbolic plan
is the unit disk again, but in the plane t = 0. But what represents the image of a hyperbolic line? One easily to notice that it is about circles situated in the unit disk and which are orthogonal on the border of the disk in question or are associated to diameters in the latter. Poincaré disk model possesses an important property which is that the angular gap between two circles images of two lines is the same measure that the angle describes by two lines in the hyperbolic plan 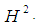 We say that the model is conformal.The continuation of our work will present the practical use of the properties of the hyperbolic geometry such we present it in the current section.
We say that the model is conformal.The continuation of our work will present the practical use of the properties of the hyperbolic geometry such we present it in the current section.4. Practical Use of the Hyperbolic Geometry
- Appeared around of 19th century, the hyperbolic geometry verifies four first ones Euclid’s postulate, but not the fifth. The Models the most popular is the model of the record of Poincaré which we use in this paper. This model is represented by Figure 6.
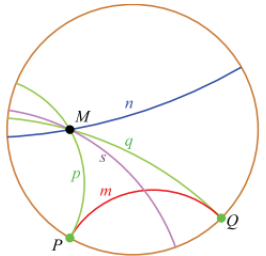 | Figure 6. Poincaré’s disk model: inside the open disc, the points of the hyperbolic plane |
4.1. Tiling of the Hyperbolic Plane
- From a famous theorem established by Poincaré at the end of the 19th century, we know that there are infinitely many tilings of the hyperbolic plan, every product by the reflection of a polygon P in the sides and, in a recurring way, in the reflection of the images on their sides, provided that the number p sides of P and the number q copies of P which can be put around a point A and exactly the cover of neighbourhood of A without satisfied overlapping the relation:
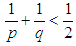 | (9) |
 | Figure 7. Tiling of the hyperbolic plane with 3-regular tree |
 thus, we call on to a metrics of Poincaré which is an isometry invariant given by the formula:
thus, we call on to a metrics of Poincaré which is an isometry invariant given by the formula: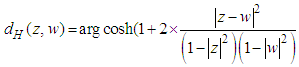 | (10) |
4.2. Information’s Routing Process in Hyperbolic Tree
- The management of the communication between devices on the Internet of things is made by the use of the specific mechanism of indexing. This process combines one greedy routing [22] and a routing by holes bypass [23]. It concerns a kind of without knowledge of the neighbourhood, which remains very effective in a context of dynamic system Dynamic context characterized by the connection and the voluntary disconnection of nodes or by failure of the system.By default a message is sent into eager’s mode via the calculation of the closest node to the destination. Thus, the following relay runner is chosen in a way distributed among nodes situated in the zone of relayage (immediate Neighbourhood of the current node) in the time a phase of the application with a period of additional withdrawal.This delay is a function of the hyperbolic distance of the relay runner in the node of the destination. However, in certain cases, when this zone is deprived of candidate node to relieve the message, the progress by the holes bypass is used. It consists initially in the discovery of the neighbourhood, then to cross in the second time with the planarization of the graph resulting from the neighbourhood before the choice of the relay runner among nodes resulting from the planar graph according to the rule “right hand” [24].In the geographical routing, the purpose of the planarization is to avoid buckles during the routing process and require to have a knowledge of the 2-neighbourhood to have a planar graph in an environment of realistic radio operator for Internet of things with the precise hyperbolic contact.Figure 8 illustrates the routing of message of connection or search for information in the disc of Poincaré that which we propose.
 | Figure 8. Routing process with Internet of things system |
5. Building and Function of Our IoT System
- In order to show in a precise way, how our system of cloud for the Internet of things run, it is important to show the various algorithms which take part in the good management of devices. These algorithms are in particular that of the creation of our structure of hyperbolic tree, thus that of the inter-devices connections between devices.

5.1. Building of the Addressing’s tree
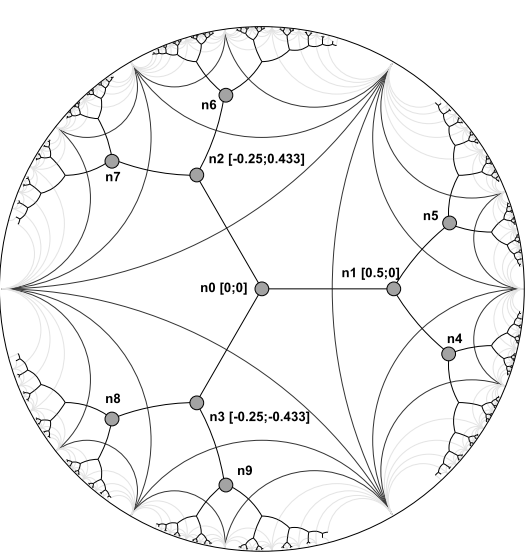
- According to Algorithm 1, the first step in the creation of our hyperbolic tree is to start the first device and to choose the degree of the addressing’s tree associated with the hyperbolic tree. We recall that the hyperbolic coordinates (i.e. a complex number) of a node of the addressing’s tree are used as the address of the corresponding device in the system. A node of the tree can give the addresses corresponding to its children in the tree. The degree determines how many addresses each device will be able to give. The degree of the tree is defined at the beginning for all the lifetime of the Internet of things system. The latter is then built incrementally, with each new device joining one or more existing device. Over time, the devices will leave the system until there is no peer left, which is the end of the system. This method is scalable because unlike [25] [26], we do not have to make a two-pass algorithm over the whole network to find its highest degree. Also in our system, a device can connect to any other device at any time in order to obtain an address. It is about a system of structured Peer-to-Peer based on a Distributed Hash Table (DHT).In the process of building of addressing’s tree, the first step is to define the degree of the tree because he allows to build the dual, namely the regular q-gon. We fix the root of the tree originally and we begin the tiling at the origin of the disk in the function of q. Every splitting of the space to create disjoint subspaces is assured when half spaces are the tangent; where from the primal is an infinite q-regular tree. We use the tree of theoretical infinity q-regular to build the fixation greedy for our tree of q-regular. Thus, the degree of the regular tree is the number of the sides of the polygon was used to building the dual (see Figure 7). In other words, the space is assigned for q devices children. Every device repeats the calculation for its own half of the space. In half of the space, the space is again assigned for q − 1 children. Every child can distribute its addresses in its half space. Algorithm 2 shows how to calculate the addresses that can be given to the children of a device. The first device takes the hyperbolic address (0; 0) and is the root of the tree. The root can assign q addresses. q is the number of half space created in the hyperbolic plane for each one.
 This distributed algorithm assures that devices are contained in different spaces and have unique address and coordinates. All the steps of the presented algorithm are suited for the distributed and asynchronous calculation. This algorithm allows the allocation of addresses as coordinates in the dynamic topology. As the global knowledge of the system is not necessary, a new device can obtain its coordinates (address) by asking an existing device to be its parent and to give its address for him. If the wanted device has already given all its addresses, the new device has to ask an address in another existing device. When the last one obtains an address, it calculates the addresses (i.e. hyperbolic coordinates) of its future devices that can potentially connect itself to the system. The tree of addressing builds itself by iteration at the same time as the system.
This distributed algorithm assures that devices are contained in different spaces and have unique address and coordinates. All the steps of the presented algorithm are suited for the distributed and asynchronous calculation. This algorithm allows the allocation of addresses as coordinates in the dynamic topology. As the global knowledge of the system is not necessary, a new device can obtain its coordinates (address) by asking an existing device to be its parent and to give its address for him. If the wanted device has already given all its addresses, the new device has to ask an address in another existing device. When the last one obtains an address, it calculates the addresses (i.e. hyperbolic coordinates) of its future devices that can potentially connect itself to the system. The tree of addressing builds itself by iteration at the same time as the system.5.2. Referencing and Binding in Poincaré Disk Model
- In this section, we present our structure of IoT based on the hyperbolic algorithm of greedy routing presented in the Section 4.2. We explain how our system stores and retrieves information in the peers of the network. With the departure, every new member of the system chooses a name which identifies the device where it is made. This name is protected by the device as long as the system exists.Then, the device obtains an hyperbolic address and becomes an entity of the system while connecting itself to the addressing’s tree. With each entity of the system is associated a pair (name, addresses). This pair makes it possible to create a link between the name and the address called binding because it is stored in the DHT by using the name as key. If the name of the entity is already a key of our system, then an error message is sent in answer to the entity so that it chooses another name, thus the structure of our IoT system itself guarantees that the names are single. To store the pair (name, addresses) associated to the device in the system, this latter creates a key by hashing its name with the algorithm SHA-2. The key of 512 bits is arbitrarily divided into 16 sub-keys of 32 bits. The system selects the first sub-key then and computes an angle by a linear transformation. The angle is given by equation 2. This angle gives us a virtual point on the circle.
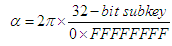 | (11) |
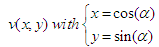 | (12) |
 | Figure 9. Hyperbolic IoT system |
6. Management of our IoT System
6.1. How to Cope with Dynamic Topologies
- The routing in the hyperbolic plan is robust as long as the integrity of the tree is maintained. In effect, the embedded greedy of [27] depends on the subjacent connectivity of the spanning tree (or planar graph) embedded. In a real IoT environment, it is expected that the failures of the links or the entities often arrive. Clearly, the disadvantage of this method is resistance to breakdowns [28]. This is why, we consider two levels of breakdowns:• the first level corresponds to the breakdowns of q-regular addressing’s tree.• the second level corresponds to the breakdowns in the graph of the IoT system.On the first level, if a link in the tree is then broken the hyperbolic greedy routing will fail for the ways crossing this link. Worse, if an entity other than a leaf breaks down, the tree is broken in a forest of with more q trees and thus disturbs the connectivity of the tree. We can then use techniques of repair or maintenance of drill of tree such as the random walk which is a natural approach for the exploration of the graphs. The idea is attractive, but in our case we cannot guarantee the consistency of the addresses when the tree amalgamates, in other words, that could create buildings minimum. Indeed, fusion without an update of the addresses of the nodes of the sub-tree is not acceptable. Moreover, the random walk is not efficient in hyperbolic space because it aims towards the infinity. But in every case, the Achilles’ heel remains the root. Therefore, to mitigate these breakdowns, it is necessary to use an alternative method of routing. If the tree of addressing is broken, two approaches can be used to restore connectivity:• method of purging: consist in purging the addresses of the nodes starting from the link or device in breakdown and to reallocate the addresses with all these nodes.• method of restoration: consist in restoring the tree in substitute the defective link by one new identical link or broken down device by a new device with the same connections.The first solution that we call the method of purging can be expensive if the size of the IoT system is very great and/or if the nodes beyond the breakdown are numerous because that can carry out to readdress a vast part of entities. The second solution that we call the method of restoration is less expensive because the addresses are kept but the implementation is more complex in the case of the breakdown of an entity. Indeed, it is difficult for a new entity to be configured with same connections as those of the failing entity that it replaces.On the second level, if the link of the IoT system is not touched by the breakdown in the addressing’s tree or if it is an entity breaks into leaf the hyperbolic greedy routing then is carried out without error through the ways being able to be longer. The addressing’s tree is built on the overlay network, which means that there exist subjacent links, potentially short cuts which can become the only possible road. In the course of time, when the solutions above are used to restore the addressing’s tree, other techniques can be used to guarantee the success of the routing. A first technique, for the downward losers their ancestor, consists in trying to establish a connection with their first ancestor (i.e. grandparent) as well as with their brothers. If they make a success of the hyperbolic greedy routing will be guaranteed, if not the addressing’s tree remains broken and the greedy algorithm fails because of the problem of “local minimum”. To overcome this problem, heuristics called “Gravity-Presses (GP)” is presented in [28] and also used in [29]. When a message arrives in an entity which is a “local minimum” it enters in mode “presses”. In this mode, the message maintains a list of the nodes which it crosses and the number of times that it crosses them. This continuous process until the message finds an entity whose distance with the destination is smaller than the distance with the “local minimum”. The solution put forward requires the storage of much information in the heading of the message which can be difficult and heavy to establish.
6.2. Storage by Replication Strategy in the IoT System
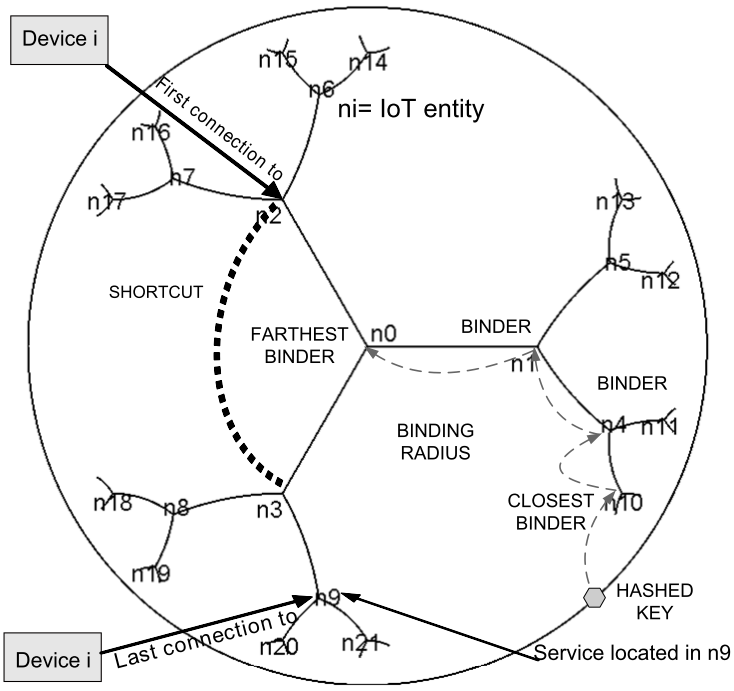
- As described in Section 4.2., the system guarantees that the names given are single and makes it possible by linear transformation via algorithm SHA-512 to compute 16 different points on the Poincaré disc model.Now, the entity determines the hyperbolic coordinates of the node nearest to this virtual point; this node is a binder of the couple (name, addresses). An example of the procedure of storage is shown in Figure 10). Thus to store in the entity n10, a request is sent to storage computed. This request is routed by using the hyperbolic greedy routing described in Section 4.2. If the request fails because the storage cannot be reached, because of a node or a link failed, then the request is redirected towards the storage one nearest which is the father of storage computed.
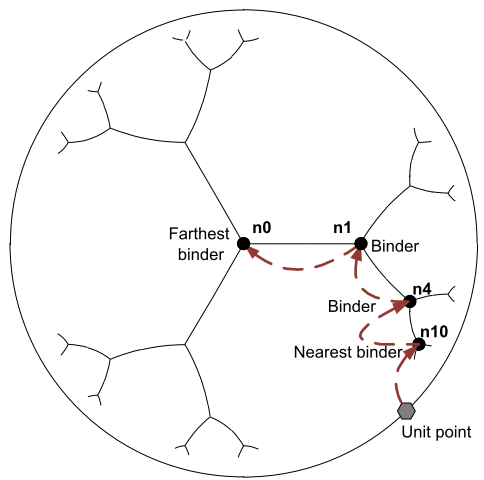 | Figure 10. Binder use for storage process |
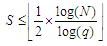 | (13) |
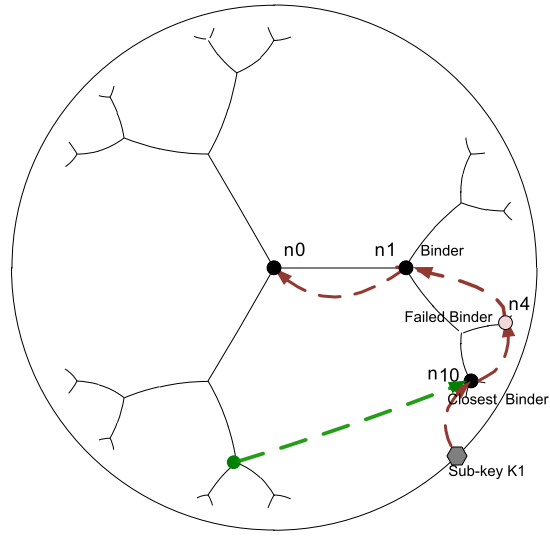 | Figure 11. Radial replication process |
 | Figure 12. Circular replication process |
7. Experimental Study of Reliability and Scalability Properties
- In this section, we present the results of the simulations that we have run and we have evaluated the performances in term of scalability and reliability, of our devices addressing system. Our IoT system is considered as dynamic (the phenomenon of churn is applied). We use the Peersim [30] simulator for IoT system simulation and it allows to service name following the uniform distribution. Excepted, the study on the floating point precision issue, our simulation involves the following parameters:• number of devices connected and used to store different kind of services is equal to 10000 in the starting up;• we consider that our IoT system is dynamic and the rate of churn varying from 10% to 60%;• we consider a simulation performed during 2 hours;• the leaving and joining of the devices follows an exponential distribution as well as the inserting and the deleting of the services of the system associated.
7.1. Analysis of the Number of Sub-keys
- Figure 13 presents the evolution of the number of primary binders according to the number of sub-keys chooses as the simulation. This plot shows a continuous growth of the number of binders according to the number of sub-keys. Furthermore, we can observe that this plot is below the ideal case or the number of binders always corresponds among sub-key. The feigned plot is besides very close to the ideal plot, what shows that we have a satisfactory situation for all the levels of replication.
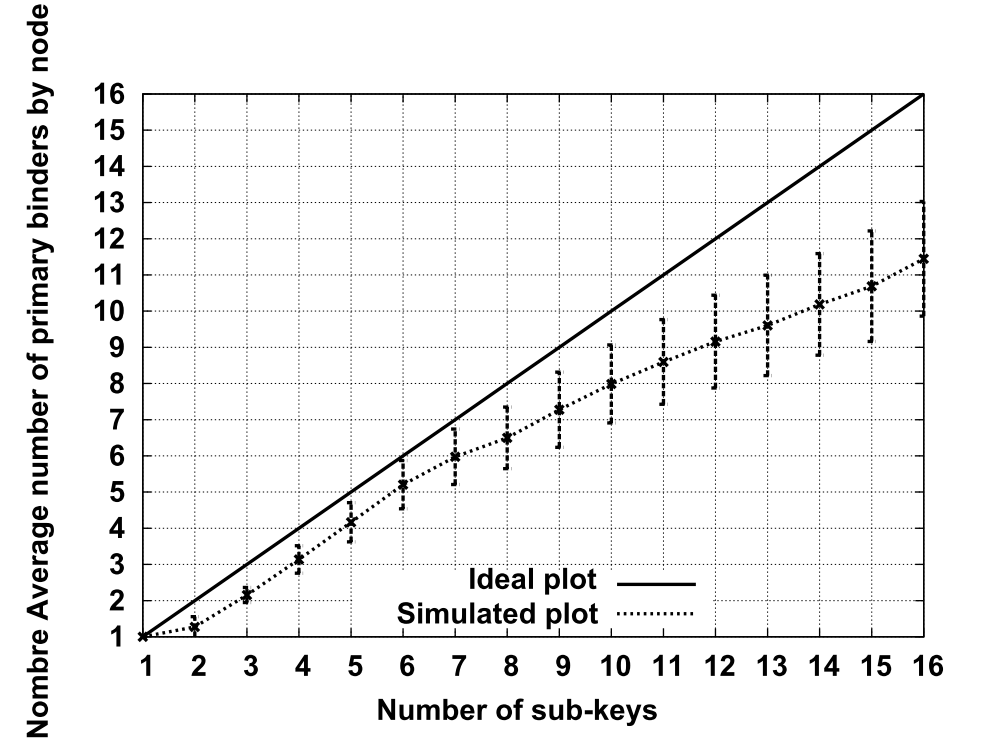 | Figure 13. Variation of binder number depending of the number of sub-keys |
7.2. Load Balancing in the IoT System
- Figure 14 shows an experimental distribution of points corresponding to the scatter plot of the distribution of devices in our IoT system. Thus, we can mark that hyperbolic-tree of our IoT system is balanced. Indeed, we can noticed by part and others around the unit circle which we have providers of services.
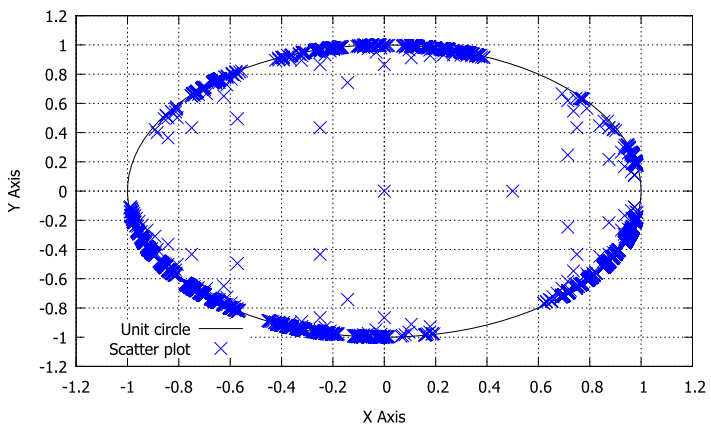 | Figure 14. Scatter plot corresponding to the distributed devices |
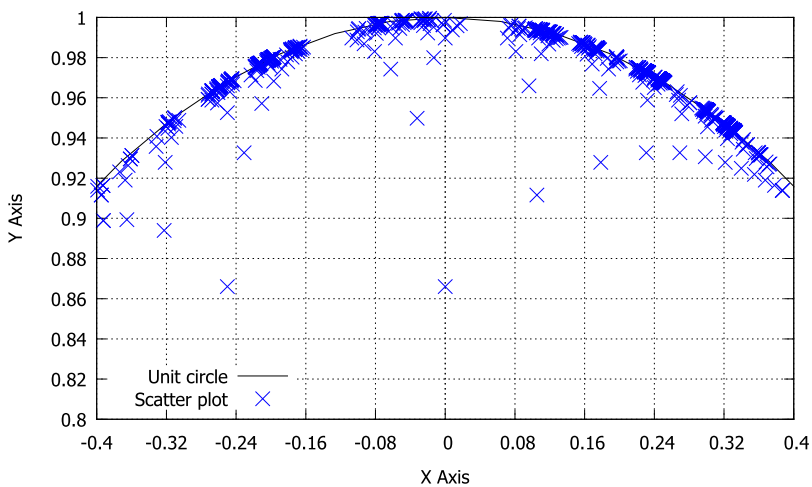 | Figure 15. Distribution of nodes in the neighbourhood of the edge of the unit circle |
8. Conclusion and Futur Work
- This paper provides the foundation of a fully distributedcontrol plane for the Internet of Things. Thus, we propose a system which uses a virtual hyperbolic frame of referenc based on the Poincaré disc model. This system has on the one hand a certain number of hyperbolic geometry properties. Furthermore, a property of robustness and reliability expressed by a strategy of replication (radial and circular) then of a scalability owing to the fact that the device has a total independence in the choice of their point among in the system.Through this study, we can realize through bound work that there is still much work to do with the domain of IoT, that is from a theoretical point of view that applied. But for the moment, no research approached the use of the Poincaré disc model in the field of IoT.This paper can be considered as a contribution brought in the context of the interconnection and the exchange between devices of the domain of the Internet of Things. We hope that it will encourage people to venture along the tracks opened in this paper and, it would be the best, to go further towards new perspectives. Us concerning, we count following this work, to suggest some solutions of repairing of the addressing's tree in situation of flash crown.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML