1. Introduction

The growth of the Internet has made cryptography is more important and critical issue in electronic application systems. Unless the system is able to provide some mechanisms to ensure security services, the system will have problems to be accepted. More reliable cryptosystems have to be proposed and, cryptography is being an essential part of today's information systems. Cryptography is the science of using mathematics to encrypt and decrypt data. It enables us to store or transmit sensitive information across insecure networks like the Internet. So that it cannot be read by anyone except the intended recipient[3].

Cryptography is one of the technological means to provide security to data being transmitted on information and communications systems. Cryptography is especially useful in the cases of financial and personal data. Hence, information security is a precondition of e-application systems when communicating over untrusted medium like the Internet.

The most effective way of data protection is encryption. A cryptography system which provides two complementing functions, encryption and decryption is called cryptosystem. Cryptosystems use encryption algorithms to determine the encryption process, the necessary software component, and the key to encrypt and decrypt the data (e.g.[1],[11]).Cryptography techniques are always employed to protect critical and confidential information against malicious attack from the intruders.

There are two main types of cryptography algorithms: symmetric-key and asymmetric-key[2]. There have been many cryptographic techniques and algorithms are well-defined in the literature such as DES, AES, RSA, and ECC[4].

In this paper, we propose a cryptosystem for Extensible Markup Language (XML) data encryption/decryption by combining the features of both symmetric key and asymmetric key cryptography. We used XML as an experimental work due to the importance of XML in data exchange in distributed systems. XML is being used across the Internet to improve compatibility between disparate Electronic Data Interchange (EDI) systems. XML designed to meet the challenges of large-scale electronic publishing. It plays an important role in the exchange of a wide variety of data on the Web[8]. There has been much research work related to information security techniques[15].

The rest of the paper is organized as follows. Section 2 gives an overview of cryptography fundamentals, followed by an explanation of cryptography types in Section 3. Section 4 presents our proposed system, and section 5 introduces the results, and finally we conclude the paper.

2. An Overview of Cryptography

The word cryptography originated from two Greek words, kryptos which means secret and graphos which means writing; hence it literally means secret writing. In particular, cryptography may be thought of as the science of secret writing, aiming at protecting data so that only the intended recipients may decrypt and read the message. A cryptosystem is composed of two complementing functions, encryption and decryption. Encryption is the conversion of data into a form, called a ciphertext that cannot be easily understood by unauthorized people based on input key. Decryption is the process of converting encrypted data back into its original form, so it can be understood using the decryption key. Encryption and decryption keys are the same for symmetric cryptosystem and different for asymmetric cryptosystem[1]. Cryptosystems are used to achieve several goals such as:

• Confidentiality is the process of keeping information private and secret so that only the intended recipient is able to understand the information.

• Authentication, which is the process of providing proof of identity of the sender to the recipient, so that the recipient can be assured that the person sending the information is who and what he or she claims to be.

• Data integrity is a service which addresses the unauthorized alteration of data. To assure data integrity, one must have the ability to detect data manipulation by unauthorized parties. Data manipulation includes such things as insertion, deletion, and substitution.

• Non-repudiation is a mechanism used to prove that the sender really sent this message. This is achieved by using a digital signature mechanism.

A fundamental goal of cryptography is to adequately address these four areas in both theory and practice. These are usually achieved through data encryption mechanism. As cryptography is the science and art of creating secret codes, cryptanalysis is the science and art of breaking those codes, with a view to finding weaknesses in them that will permit retrieval of the original data from the encrypted data, without necessarily knowing the key or the algorithm. Cryptography and cryptanalysis are two different scientific studies in direct competition with each other, the first attempts to hide a secret and the latter attempts to uncover it[3].

To ensure the security of the message, the original message is transformed to ciphertext using an encryption algorithm by the sender. And the receiver uses a decryption algorithm to transform the ciphertext back into plaintext. Encryption and decryption algorithms are called ciphers. And those algorithms operate on a set of numbers called Key. To encrypt message, we need an encryption algorithm, encryption key and the plain text. These create the ciphertext. Similarly to decrypt a message, we need a decryption algorithm, decryption key and the ciphertext. These reveal the plaintext[5].

3. Types of Cryptography

There are three types of cryptography algorithms: Symmetric-key or Secret key Cryptography, Asymmetric- key or Public key Cryptography and hash functions.

3.1. Symmetric Cryptography

In Symmetric-Key Cryptography, the same key is used by both sender and receiver. To provide privacy, this key needs to be kept secret. The traditional ciphers are substitution cipher and transposition cipher. A substitution cipher substitutes one symbol with another. And the transposition cipher does not replace the original text with different text, but moves the original text around. The most popular secret key encryption algorithms are Data Encryption Standard (DES), Triple DES, and Advance Encryption Standard (AES)[13].

DES –The Data Encryption Standard Designed at IBM during the 1970’s and officially adopted as the NIST standard encryption algorithm for unclassified data. The DES algorithm takes 56 bit and 64 bit plaintext as inputs and outputs 64 bit. In terms of strength its design has stood the test of time very well, but its relatively short key length by modern standards means that it is now considered vulnerable to brute force attacks. It is also, in software, comparatively slow.

Triple DES – Triple DES is a variation of DES. Triple-DES refers to encrypting the same 64-bit block using DES three times in sequence, using three different DES keys K1, K2 and K3. Decryption is then performed in the opposite sequence, first decrypting with K3, then decrypting with K2, and then decrypting with K1. The idea behind Triple DES is to improve the security of DES by applying DES encryption three times using three different keys.

AES – The Advanced Encryption Standard (AES) Designed in 1998 by Joan Daemen and Vincent Rijmen to replace DES algorithm. It is block cipher; It can create keys from 128 to 256-bit in length and can perform the encryption on up to 128-bit blocks of clear-text at a time. (DES is limited to 64-bit blocks). Similar to 3DES the blocks are passed to 3 layers, each layer performs a different task. Each pass encrypts the data and generates a key and the final key is applied to the ciphertext data.

Table (1) shows the time attack for some symmetric key algorithm.

Table 1. Time Table Attach Algorithm Cipher Type Key length Attack time in years DES Block 112 bits 1 x 1024 3DES Block 128 bits 1.25x 1028 AES Block 128 bits 1070

3.2. Asymmetric-Key Cryptography

This type uses two keys: a private key and a public key. Public key is used to encrypt to message whereas private key is used to decrypt. The public encryption key is made available to who wants to use it, but the private key is kept secret by the key owner. The process is explained below:

- If A wants to send a message to B, the message is encrypted by a using B’s public key.

- If B receives the message, the message is decrypted by using B’s private key. No other recipient can decrypt the message.

The most popular public key encryption algorithms are Rivest, Adi Shamir, and Leonard Adleman (RSA), and Elliptic Curve Cryptography (ECC)[4].

RSA (Rivest, Shamir, and Adleman) – RSA is the most commonly used algorithm. It is named by its inventors name Rivest, Shamir, and Adelman (RSA). It uses two numbers as the public and private keys. RSA is useful for short messages and also used in digital signatures. But it is very slow if the message size becomes long (e.g.[4],[9]).

RSA is a public key cryptosystem that was invented by Rivest, Shamir and Adleman, hence the name RSA which takes the first letter of each name. With RSA, two keys are involved which are public key and private key. As the names imply, public key can be made available to others while the private key must be kept in secret. The relationship between the public key and private key is such that, public key decrypts a message encrypted by private key, and private key decrypts a message encrypted by public key. This type of cryptography is also known as asymmetric key cryptography, which is different from symmetric key cryptography where a single key is both used for encryption and decryption. The strength of RSA algorithm relies on the difficulty of factoring the number N into two prime factors p and q. If the factoring is successful, p and q can be used to find the private key[6].

ECC (Elliptic Curve Cryptography) – ECC was discovered in 1985 by Victor Miller (IBM) and Neil Koblitz. The public key is created by agreeing on a standard generator point in an elliptic curve group (elliptic curve mathematics is a branch of number theory) and multiplying that point by a random number (the private key). Although the starting point and public key are known, it is extremely difficult to backtrack and derive the private key.

Once the public key is computed by ECC, it can be used in various ways to encrypt and decrypt. One way is to encrypt with the public key and decrypt with the private one. ECC allows a digital signature to be signed with a private key and verified with the public key[7],[14].

3.3. Hash Functions

One of the fundamental primitives in modern cryptography is the cryptographic hash function; a hash function is a one-way hash is a function (usually mathematical) that takes a variable-length string, a message, and compresses and transforms it into a fixed-length value referred to as a hash value. A hash value is also called a message digest. Here, hashing is used to perform one way encryption. One way means that once the information has been encrypted there is no way to retrieve the original information from the hashed form.

The most common cryptographic uses of hash functions are with digital signatures and for data integrity (e.g.[10],[13]). Hash algorithms that are in common use today include:

• Message Digest Service Algorithms (MD) - The message digest kinds of encryption algorithms provide encryption of 128 bits in strength and are designed to be fast and simple. Current standards are MD2, MD4 and MD5.

• Secure Hash Algorithm (SHA) - Describes Secure Hash Algorithm four algorithms SHA-1, SHA-256, SHA-384, and SHA-512. The four hash algorithms specified in this standard are called secure because, for a given algorithm, it is computationally infeasible to find a message that corresponds to a given message digest, and to find two different messages that produce the same message digest.

4. The Proposed Cryptosystem

The basic idea of our proposed cryptosystem is using the combination of both RSA and Shift cipher algorithms. The shift ciphering is symmetric key cryptography algorithm using a shared key for both encryption (converting plain text to cipher text) and decryption (converting cipher text to plain text) and here the ASCII characters are substituted as numbers from 0 to 127 and they are shifted and XORED according to a key. Then, the shifted numbers are transmitted and at the receiver the original numbers are obtained again by shifting using a key which is shared along with the transmitter key. The proposed system is composed of several modules. The following subsections explain each module.

4.1. Key Generation for RSA algorithm

The RSA involves a public key and a private key. The public key we used for encrypting document and the private key we used for decrypting document. To generate public and private keys we use the following steps:

1. Generate two large random primes, p and q.

2. Compute n = p.q and (φ) phi = (p-1) (q-1).

3. Choose an integer e, 1 < e < phi, such that:

gcd(e, phi) = 1.

4. Compute the secret exponent d, 1 < d < phi, ed ≡ 1 (mod phi).

Where:

• The public key is (n, e) and the private key is (n, d).

• The values of p, q, and phi should also be kept secret.

• n is known as the modulus.

• e is known as the public exponent or encryption exponent.

• d is known as the secret exponent or decryption exponent.

• Encrypting the massage by c = m^e mod n.

• Decrypting the message by m = c^d mod n.

4.2. Encryption

In this process sender A does the following:

1. Generate data.

2. Compute the hash value for data.

3. Generate digital signature by encrypting hash value.

4. Shift the data by affine cipher.

5. Encrypt the data using RSA algorithm.

6. Store data or transmit.

4.3. Decryption

Recipient B does the following:

1. Generate Encrypted data.

2. Decrypt hash value to generate signature.

3. Decrypt the data using RSA algorithm.

4. Re-shift the data by affine cipher.

5. Computing the hash for data.

6. Compare hash values if they are same, the signature is “good”, otherwise bad.

4.4. Digital Signing

In this process, sender A does the following:

1. Generate the keys exactly as key in the RSA.

2. Create a digest from the message D = h(M) “hash value”.

3. Uses the private key (n, d) to compute the signature s = m^d mod n.

4. Send the signature s to the recipient, B.

Public-key algorithms can also be used to form digital signatures. Digital signatures authenticate the identity of a sender (if we trust the sender's public key) and help protect the integrity of data. Using a public key generated by A, the recipient of A's data can verify that A has sent it by comparing the digital signature to A's data and A's public key.

4.5. Signature verification

In this process, recipient B does the following:

1. Use sender A's public key (n, e) to compute integer v = s^e mod n.

2. Extract the message digest from this integer.

3. Independently compute the message digest of the signed information.

4. If both message digests are identical, the signature is valid.

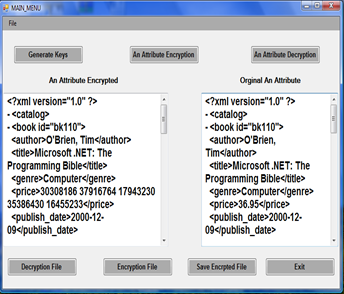Figure 1. XML data element Encryption/Decryption

5. Experimental Work

In order to evaluate our cryptosystem, we have implemented different examples to encryption and decryption XML document, and finally we evaluated the strength of our cryptosystem from point its safety and resistance of attacks. We introduce some examples of our developed system.

5.1. Example 1

Figure 1 shows the process of encrypting an element within an XML document. In this example we have tested our cryptosystem through encrypting some elements. We have selected a particular element 'price' within the XML file, and encrypt such an element.

5.2. Example 2

We have tested our cryptosystem through exchanging encrypted XML documents between distributed systems across internet network. Figure 2 shows this process, we received an encrypted XML document, then we have decrypted this document got the original document.

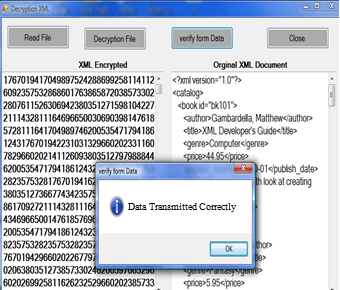Figure 2. Signed document Encryption/Decryption

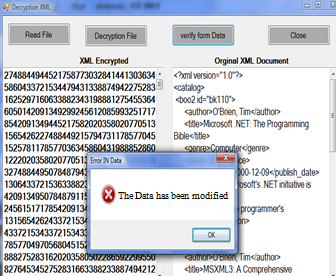Figure 3. XML Document Encryption/Decryption

5.3. Example 3

Also, we have tested the cryptosystem in another example, where, we changed just one character in document after encrypted it, and we transmitted this document into a user in another place over Internet. The receiver decrypted the document, and detected that document has been altered. Figure 3 shows the detection of this process change.

6. Results and Evaluation

In order to prove the strength and safety of our cryptosystem, we have evaluated extent of strength of our cryptosystem via calculating the range of time to decode key “cryptanalysis’’. Where the strength of any system used in the encryption is discerning in accordance with the required time to decode a key. The strength of encryption algorithm is calculated using the following equations:

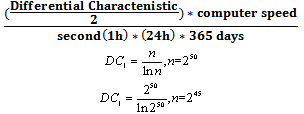Where, DC₁ differential characteristic keys of RSA algorithm. n is the number of bits of key, where, the time needs by an attacker to solve some equivalent of the integer factorization problem to factor N. In this case the bits of key are 2⁴⁵ .

DC₂ = 2⁶⁷

DC₂ means the number of bits of key for affine cipher technique and number of bits of key for encryption technique of key of RSA algorithm. We done decrypted the public keys before transmitting them. The total number of bits for our cryptosystem is:

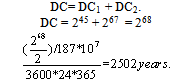The amount of time required to break key of algorithm is 2502 years, however, it will be sufficient against brute force attacks. In general, our cryptosystem provide high security, it provides a powerful means for masking information to protect it, where, achieves the fundamental requirements of cryptography that provide security adequately. It provides a powerful means of verifying the authenticity of data, confidentiality, non-repudiation, and the data integrity.

7. Conclusions

Security has always been important in electronic applications. Cryptography techniques are employed to protect critical and confidential information against malicious attack from the intruders. The security of a cryptographic system depends heavily on the strength of its keys. If an attacker can obtain your keys he can decrypt your messages. In this paper, we have proposed a cryptosystem for encrypting/decrypting XML documents. We found the results of our simulation are very much satisfactory for practical implementation as a cryptosystem for XML data. Using XML as an experimental work was due to the importance of XML in data exchange over the Web.