1. Introduction

Rough set theory, introduced by Zdzislaw Pawlak, is a mathematical tool for representing, reasoning and decision making in the case of uncertain information. This theory deals with the approximation of sets or concepts by means of equivalence relations and is considered as one of the first non-statistical approaches in data analysis. Several interesting applications of the theory have come up, in particular, in Artificial Intelligence and Cognitive Sciences. The main advantage of rough set theory in data analysis is that, it does not require any preliminary or additional information of the data. The main difference between rough sets and fuzzy sets is that the rough sets have precise boundaries whereas fuzzy set theory is generally based on ill-defined sets of data, where the bounds are not precise and hence fuzzy predictions tend to deviate from exact values. The lower and upper approximations of a set are analogous to the interior and closure operations in a topology generated by data. In this paper, we have introduced a new topology called rough topology in terms of lower and upper approximations of a rough set and we have applied the concept of topological basis to find the deciding factors for chikungunya and diabetes.

2. Preliminaries

Definition 2.1 [6]: Let U be a non-empty finite set of objects called the universe and R be an equivalence relation on U named as the indiscernibility relation. The pair (U,R) is called the approximation space. Let X be a subset of U.

i) The lower approximation of X with respect to R is the

set of all objects, which can be for certain classified as X with respect to R and it is denoted by R_*(X). That is, R_*(X)= 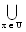{R(x):R(x) ⊆ X} where R(x) denotes the equivalence class determined by x.

ii) The upper approximation of X with respect to R is the set of all objects, which can be possibly classified as X with respect to R and it is denoted by R*(X). That is, R*(X) = 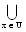{R(x):R(x) ∩X ≠ }.

iii) The boundary region of X with respect to R is the set of all objects, which can be classified neither as X nor as not-X with respect to R and it is denoted by B_RX. That is, B_R(X)= R*(X) – R_*(X).

The set X is said to be rough with respect to R if R*(X) ≠ R_*(X). That is, if B_R(X) ≠ .

Proposition 2.2[6]: If (U, R) is an approximation space and X and Y are subsets of U, then

i) R_*(X) ⊆ X ⊆ R*(X)

ii) R_*()= R*()= and R_*(U) = R*(U)= U

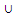iii) R*(X Y)= R*(X) 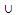R*(X)

iv) R_*(X 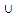Y) ⊇ R_*(X) 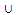R_*(Y)

v) R_*(X 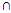Y)= R_*(X) 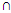R_*(Y)

vi) R*(X 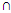Y) ⊆ R*(X) 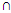R*(Y)

vii) R_*(X) ⊆ R_*(Y) and R*(X) ⊆ R*(Y) whenever X ⊆ Y

viii) R_*(X^C)= [R*(X)]^C and R*(X^C) = [R_*(X)]^C

ix) R_*R_*(X)= R*R_*(X) = R_*(X)

x) R*R*(X)= R_*R*(X)= R*(X)

Remark 2.3: R*: P(U) → P(U) satisfies the Kuratowski closure axioms that

i) R*() =

ii) X ⊆ R*(X)

iii) R*(X 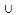Y) = R*(X) 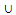R*(X)

iv) R*R*(X) = R*(X) for all subsets X and Y of U

If F = {X ⊆ U / R*(X) = X} ,using conditions (i) to (iv), we see that and U are in F; X 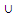Y ∈ F whenever X and Y are in F and 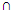Xα ∈ F for all Xα in F. Therefore, the family T, of complements of members of F is a topology on U. Thus, F is the family of T-closed sets. Also, Cl(X) = R*(X). Therefore, R* is the Kuratowski's closure operator.

Remark 2.4: Since R_*: P(U) → P(U) satisfies the following properties that

i) R_*(U) = U

ii) R_*(X) ⊆ X

iii) R_*(X 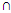Y) = R_*(X) 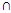R_*(Y)

iv) R_*R_*(X) = R_*(X) for all subsets X and Y of U,

the operator R_* is the interior operator.

3. Rough Topology

In this section we introduce a new topology called rough topology in terms of the lower and upper approximations.

Remark 3.1: Let U be the universe of objects and R be an equivalence relation on U. For X 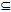U, we define 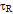= {U , , R*X, R*(X), BRX}, where R*(X), R*(X) and BR(X) are respectively the upper approximation, the lower approximation and the boundary region of X with respect to R. We note that U and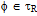. Since R*(X) R*(X), R*(X) R*(X) = R*(X) R. Also, R*(X) BR(X)= R*(X) R and R*(X) BR(X) = R*(X) R. Also, R*(X) R*(X)= R*(X) R ; R*(X) BR(X)= BR(X) R and R*(X) BR(X)= R. Remark 3.1: Let U be the universe of objects and R be an equivalence relation on U. For X U, we define R = {U , , R*X, R*(X), BRX}, where R*(X), R*(X) and BR(X) are respectively the upper approximation, the lower approximation and the boundary region of X with respect to R. We note that U and R. Since R*(X) R*(X), R*(X) R*(X) = R*(X) R. Also, R*(X) BR(X)= R*(X) R and R*(X) BR(X) = R*(X) R. Also, R*(X) R*(X)= R*(X) R ; R*(X) BR(X)= BR(X) R and R*(X) BR(X)= R.

Definition 3.2: Let U be the universe, R be an equivalence relation on U and τ_R = {U,, R_*(X), R*(X), B_R(X)} where X ⊆ U. τ_R satisfies the following axioms:

i) U and ∈ τ_R.

ii) The union of the elements of any subcollection of τ_R is in τ_R.

iii) The intersection of the elements of any finite subcollection of τ_R is in τ_R.

τ_R forms a topology on U called as the rough topology on U with respect to X. We call (U, τ_R, X) as the rough topological space.

Example 3.3: Let U ={a,b,c,d,e}, U/R={{a,b},{c,d},{e}}, the family of equivalence classes of U by the equivalence relation R and X = {a,c,d}. Then R*(X) = {a,b,c,d}, R_*(X) = {c,d} and B_R(X) = {a,b}. Therefore the rough topology τ_R = {U, , {a,b,c,d}, {c,d},{a,b}}.

Proposition 3.4: If τ_R is the rough topology on U with respect to X, then the set B = {U, R_*(X), B_R(X)} is the basis for τ_R.

Proof:

i) 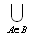A = U.

ii) Consider U and R*(X) from B. Let W = R_*(X). Since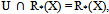 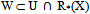and every x in 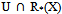belongs to W. If we consider U and BR(X) from B, taking W = B_R(X), 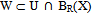and every x in 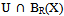belongs to W, since 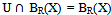. And when we consider R_*(X) and B_R(X), 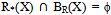. Thus, B is a basis for R.

Definition 3.5: Let U be the universe and R be an equivalence relation on U. Let τ_R be the rough topology on U and β_R be the basis for τ_R. A subset M of A, the set of attributes is called the core of R if β_M ≠ β_R-(r) for every r in M. That is, a core of R is a subset of attributes which is such that none of its elements can be removed without affecting the classification power of attributes.

4. Rough Topology in Chikungunya

Here we consider the problem of Chikungunya, a disease that is transmitted to humans by virus- carrying Aedes mosquitoes. There have been recent breakouts of CHIKV associated with severe illness. It causes fever and severe joint pain. Other symptoms include muscle pain, headache and nausea. Initial symptoms are similar to dengue fever. It is usually not life threatening. But the joint pain can last for a long time and full recovery may take months. Usually patient gets lifelong immunity from infection and hence re-infection is very rare. In recent decades the disease has spread to Africa and Asia, in particular, the Indian subcontinent.

Consider the following information table giving data about 8 patients.

Table 1. Patients Joint pain (J) Head- ache(H) Nausea (N) Temperature Chikungunya P1 Yes Yes Yes High Yes P2 Yes No No High No P3 Yes No No High Yes P4 No No No Very high No P5 No Yes Yes High No P6 Yes Yes No Very high Yes P7 Yes Yes No Normal No P8 Yes Yes No Very high Yes

The columns of the table represent the attributes (the symptoms for chikungunya) and the rows represent the objects (the patients). The entries in the table are the attribute values. The patient P₅ is characterized by the value set (Joint pain, No), (Headache, Yes), (Nausea, Yes), (Temperature, High) and (Chikungunya, No), which gives information about the patient P₅. In the table, the patients P₁, P₂, P₃, P₆, P₇ and P₈ are indiscernible with respect to the attribute 'Joint pain'. The attribute 'Joint pain' generates two equivalence classes, namely, {P₁,P₂,P₃,P₆,P₇,P₈} and {P₄,P₅}, whereas the attributes 'Joint pain' and 'Headache' generate the equivalence classes {P₁, P₆, P₇, P₈}, {P₂,P₃},{P₄} and {P₅}. The equivalence classes for the attributes Joint pain, Headache, Nausea and Temperature are {P₁}, {P₂,P₃},{P₄},{P₅},{P₆,P₈} and {P₇}. For the set of patients having chikungunya, the lower approximation = {P₁,P₆,P₈} and the upper approximation = {P₁, P₂, P₃, P₆, P₈} and hence the boundary region = {P₂, P₃}. Hence the patients P₂ and P₃ cannot be uniquely classified in view of the available knowledge. The patients P₁, P₆ and P₈ display symptoms which enable us to classify them with certainty as having chikungunya. In our case, the symptoms Jointpain, Headache, Nausea and Temperature are considered as the condition attributes and the disease chikungunya is considered as the decision attribute. Not all condition attributes in an information system are necessary to depict the decision attribute before decision rules are generated. It may happen that the decision attribute depends not on the whole set of condition attributes but on a subset of it and hence we are interested to find this subset which is given by the core. Here U = {P₁,P₂,...,P₈}.

Case1: Let X = {P₁,P₃,P₆,P₈}, the set of patients having chikungunya. Let R be the equivalence relation on U with respect to the condition attributes. The family of equivalence classes corresponding to R is given by U/I(R) = {{P₁}, {P₂,P₃}, {P₄}, {P₅}, {P₆,P₈}, {P₇}}. The lower and upper approximations of X with respect to R are given by R_*(X) = {P₁,P₆,P₈} and R*(X)= {P₁,P₂,P₃,P₆,P₈}. Therefore, the rough topology on U with respect to X is given by τ_R = {U, , {P₁,P₆,P₈}, {P₁,P₂,P₃,P₆,P₈}, {P₂,P₃}}.The basis for this topology τ_R is given by β_R = {U, {P₁,P₆,P₈},{P₂,P₃}}. If we remove the attribute 'Joint pain' from the set of condition attributes, the family of equivalence classes corresponding to the resulting set of attributes is given by U/I(R-(J)) = {{P₁,P₅}, {P₂,P₃}, {P₄}, {P₆,P₈}, {P₇}}. The corresponding lower and upper approximations are given by (R-(J))_*(X)= {P₆,P₈}; (R-(J))^*(X)= {P₁,P₂,P₃,P₅,P₆,P₈} and hence τ_R-(J) ={U,, {P₆,P₈}, {P₁,P₂,P₃,P₅,P₆,P₈}, {P₁,P₂,P₃,P₅}} and its basis β_R-(J)={U,{P₆,P₈}, {P₁,P₂,P₃,P₅}}≠ β_R. If we remove the attribute 'Headache' from the set of condition attributes, the family of equivalence classes corresponding to the resulting set of attributes is given by U/I(R-(H))={{P₁},{P₂,P₃}, {P₄},{P₅}, {P₆,P₈},{P₇}} which is the same as U/I(R) and hence τ_R-(H) = τ_R and β_R-(H) = β_R. On removal of the attribute 'Nausea', we get U/I(R-(N))={{P₁},{P₂,P₃}, {P₄},{P₅},{P₆,P₈}, {P₇}}= U/I(R) and hence τ_R-(N) = τ_R and β_R-(N) = β_R. When the attribute 'Temperature' is omitted, U/I(R-(T)) = {{P₁}, {P₂,P₃}, {P₄}, {P₅}, {P₆,P₇,P₈}}. (R-(T))_*(X)={P₁}; (R-(T))*(X)={P₁,P₂,P₃,P₆,P₇,P₈}. Therefore,τ_(R-(T))={U,, {P₁}, {P₁,P₂,P₃,P₆,P₇,P₈},{P₂,P₃,P₆,P₇,P₈}} and its basis β_R-(T) = {U, {P₁}, {P₂,P₃,P₆,P₇,P₈}} ≠ β_R. If M = {J,T}, then the basis for the rough topology corresponding to M is given by β_M = {U,{P₆,P₈}, {P₁,P₂,P₃}}. Also β_M ≠ β_R-(x) for all x in M. Therefore, CORE(R) = {J,T}.

Case2: Let X ={P₂,P₄,P₅,P₇},the set of patients not having chikungunya. Then U/I(R) = {{P₁}, {P₂,P₃}, {P₄}, {P₅}, {P₆,P₈}, {P₇}}. R*(X) = {P₄,P₅,P₇} and R*(X) = {P₂,P₃,P₄, P₅,P₇}. Therefore τ_R = {U,, {P₄,P₅,P₇}, {P₂,P₃,P₄,P₅,P₇}, {P₂,P₃}} and β_R = {U, {P₄,P₅,P₇},{P₂,P₃}}. Omitting the attribute 'Jointpain', U/I(R-(J)) = {{P₁,P₅}, {P₂,P₃}, {P₄}, {P₆,P₈}, {P₇}}. (R-(J))_*(X) = {P₄,P₇}; (R-(J))*(X) = {P₁,P₂,P₃,P₄,P₅,P₇} and hence τ_R-(J) = {U, , {P₄,P₇}, {P₁,P₂,P₃,P₄,P₅,P₇}, {P₁,P₂,P₃,P₅}} and its basis β_R-(J) {U,{P₄,P₇}, {P₁,P₂,P₃,P₅}} ≠ β_R. If the attribute 'Headache' is removed, U/I(R-(H)) = {{P₁}, {P₂,P₃}, {P₄}, {P₅},{P₆,P₈}, {P₇}} which is the same as U/I(R) and hence β_R-(H) = β_R. On removal of the attribute 'Nausea', we get U/I(R-(N)) = {{P₁}, {P₂,P₃}, {P₄}, {P₅}, {P₆,P₈}, {P₇}},which is the same as U/I(R) and hence τ_R-(N) = τ_R and β_R-(N) = β_R. When the attribute 'Temperature' is omitted, U/I(R-(T)) = {{P₁}, {P₂,P₃}, {P₄}, {P₅}, {P₆,P₇,P₈}}. (R-(T))_*(X) = {P₄,P₅}; (R-(T))*(X) = {P₂,P₃,P₄,P₅,P₆,P₇, P₈}.Therefore, τ_R-(T) = {U, , {P₄,P₅}, {P₂, P₃, P₄, P₅, P₆, P₇, P₈}, {P₂,P₃,P₆,P₇,P₈}} and its basis β_R-(T) = {U, {P₄,P₅}, {P₂,P₃,P₆,P₇,P₈}} ≠ β_R. If M = {J,T}, U/I(r)= {{P₁,P₂,P₃}, {P₄,P₅}, {P₆,P₈}, {P₇}}, r_*(X)= {P₄,P₅,P₇} and r*(X)= {P₁, P₂, P₃, P₄, P₅, P₇} where r is the equivalence relation on U with respect to M. Therefore, β_M = {U, {P₄,P₅,P₇},{P₁,P₂,P₃}} ≠ β_R-(x) for every x in M. Therefore, here again, CORE(R) = {J,T}.

Observation: From both cases we conclude that 'Jointpain' and 'Temperature' are the key attributes necessary to decide whether a patient has chikungunya or not.

5. Rough Topology in Diabetes

Diabetes is a group of metabolic diseases in which a person has high blood sugar, either because the body does not produce enough insulin, or because cells do not respond to the insulin that is produced. In diabetes, glucose in the blood cannot move into cells, so it stays in the blood. This not only harms the cells that need the glucose for fuel, but also harms certain organs and tissues exposed to the high glucose levels. This high blood sugar produces the classical symptoms of polyuria (frequent urination), weight loss and polyphagia (increased hunger).

Consider the following table giving information about six patients

Table 2. Patients Frequent Urination (F) Weight Loss (W) Increased Hunger (H) Diabetes P1 Yes Yes No Yes P2 Yes No Yes Yes P3 Yes No No Yes P4 No Yes Yes No P5 No Yes No No P6 No No Yes No

Here, U = {P₁,P₂,P₃,P₄,P₅,P₆} and Frequent Urination (F), Weight Loss (W) and Increased Hunger (H) form the condition attributes. Let X ={P₁,P₂,P₃}, the set of patients having diabetes.

U/I(R) ={{P₁}, {P₂}, {P₃}, {P₄}, {P₅}, {P₆}}. The lower and upper approximations of X with respect to R are given by R_*(X) = {P₁,P₂,P₃} and R*(X) = {P₁,P₂,P₃}. Therefore B_R(X) = . The rough topology on U is τ_R = {U, , {P₁,P₂,P₃}} and its basis, β_R = {U, {P₁,P₂,P₃}}. If the attribute 'Frequent Urination' is removed from the set of condition attributes, then U/I(R-(F)) ={{P₁,P₅},{P₃},{P₄},{P₂,P₆}}. (R-(F))_*(X)= {P₃}; (R-(F))^*(X) = {P₁,P₂,P₃,P₅, P₆} and hence τ_R-(F) ={U, , {P₃}, {P₁,P₂,P₃,P₅,P₆},{P₁,P₂,P₅,P₆}} and its basis β_R-(F)= {U, {P₃}, {P₁,P₂,P₅,P₆}} ≠ β_R. If the attribute 'Weight Loss' is removed, then U/I(R-(W)) = {{P₁,P₃}, {P₂}, {P₄}, {P₆}, {P₅}}. 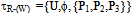(R-(W))_*(X) = {P₁,P₂,P₃} and (R-(W))*(X)={P₁,P₂,P₃} and hence and its basis β_R-(W) = {U,{P₁,P₂,P₃}} = β_R. If the attribute ' Increased Hunger' is removed, U/I(R-(H)) = {{P₁}, {P₂,P₃}, {P₄,P₅}, {P₆}}. (R-(H))_*(X) = {P₁,P₂,P₃} and (R-(H))*(X)= {P₁,P₂,P₃}. Therefore τ_R-(H) = τ_R and its basis β_R-(H) = β_R. If M ={F}, we see that β_M ≠ β_R-(F). Therefore, CORE(R) = {F}. Similarly if X is taken as the set of patients not having diabetes, then again CORE(R) = {F}.

Observation: Since the core of R has F as its only element, 'Frequent Urination' is the key attribute that has close connection to the disease diabetes .

The procedure applied in the above two cases can be put in the form of an algorithm as follows:

Algorithm:

Step 1: Given a finite universe U, a finite set A of attributes that is divided into two classes, C of condition attributes and D of decision attribute, an equivalence relation R on U corresponding to C and a subset X of U, represent the data as an information table, columns of which are labeled by attributes, rows by objects and entries of the table are attribute values.

Step 2: Find the lower approximation, upper approximation and the boundary region of X with respect to R.

Step 3: Generate the rough topology τR on U and its basis β_R.

Step 4: Remove an attribute x from C and find the lower and upper approximations and the boundary region of X with respect to the equivalence relation on C -(x).

Step 5: Generate the rough topology τ_{R -(x)} on U and its basis β_R-(x).

Step 6: Repeat steps 3 and 4 for all attributes in C.

Step 7: Those attributes in C for which β_R-(x) ≠ β_R form the core (R).

6. Conclusions

In this work, we have shown that real world problems can be dealt with the rough topology. The concept of basis has been applied to find the deciding factors of a recent outbreak 'Chikungunya' which had been reported especially, in South India and a chronic disease 'Diabetes'. We could find that Joint pain and Temperature are the deciding factors for chikungunya and frequent urination is the only deciding symptom for diabetes. It is also seen that from a clinical point of view, the rough topological model is on par with the medical experts with respect to the diseases analyzed here. The proposed rough topology can be applied to more general and complex information systems for future research. The rough set model is based on the original data only and does not need any external information, unlike probability in statistics or grade of membership in the fuzzy set theory. It is also a tool suitable for analyzing not only quantitative attributes but also qualitative ones. The results of the rough set model are easy to understand, while the results from other methods need an interpretation of the technical parameters. Thus it is advantageous to use rough topology in real life situations.