Frantisek Capkovic
Institute of Informatics, Slovak Academy of Sciences, Bratislava, Slovakia
Correspondence to: Frantisek Capkovic , Institute of Informatics, Slovak Academy of Sciences, Bratislava, Slovakia.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
The discrete-event systems (DES) modularity and supervision are utilized at synthesis of the agents cooperation. The agents are understood to be (DES) modules. They are described by place/transition Petri-nets (P/T PN)[5]. A desired strategy of the agents behaviour during the cooperation is expressed by conditions for synthesizing the DES supervisor. Then the strategy is forced on agents. Such a procedure can be utilized step-by-step also at the synthesis of more complex structures of co-operating modules (groups of agents) in order to achieve a prescribed behaviour of the global structure. The approach is illustrated by examples.
Keywords:
Agent Cooperation, Petri Nets, Supervision, Supervisor Synthesis
Cite this paper:
Frantisek Capkovic , "Supervision in Synthesis of Agents Cooperation", International Journal of Information Science, Vol. 1 No. 1, 2011, pp. 24-31. doi: 10.5923/j.ijis.20110101.04.
1. Introduction
Discrete-event systems (DES) are systems discrete in nature. Their behaviour is driven by the occurrence of discrete events. It is typical not only for software agents but also for material agents, especially in manufacturing systems (like robots, machine tools, automatically guided vehicles, etc.) and transport systems (e.g. railways). To describe DES different kinds of Petri-nets (PN) are often used. Namely, PN yield both the graphical symbolization of DES and the mathematical description. To ensure the desired cooperation of modules in a prescribed fashion the methods of DES supervising can be utilized.
1.1. Preliminaries
Here, in this paper, the P/T PN will be used. As to the structure such PN are bipartite directed graphs, i.e. h=the digraphs with two kinds of nodes (places and transitions) and two kind of edges (from places to transitions and from transitions to places). Thus PN structure is given formally as follows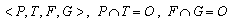 whereP is the set of the PN places pi , i = 1, 2, …, n;T is the set of the PN transitions tj, j = 1, 2, …, m;
whereP is the set of the PN places pi , i = 1, 2, …, n;T is the set of the PN transitions tj, j = 1, 2, …, m;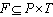 is the set of edges from places to transitions;
is the set of edges from places to transitions;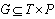 is the set of edges from transitions to places;O is the empty set.However, PN have also their dynamics. It is formally given by the following quadrupletThe system form of the PN-based model of a DES modu-le is
is the set of edges from transitions to places;O is the empty set.However, PN have also their dynamics. It is formally given by the following quadrupletThe system form of the PN-based model of a DES modu-le is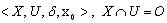 where X is the set of the PN state vectors
where X is the set of the PN state vectors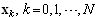 ;U is the set of the control vectors
;U is the set of the control vectors 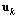 of the PN, where
of the PN, where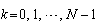 ;
;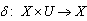 is the PN transition function expressing that a new state is given on the base of existing state and the occurrence of discrete events;
is the PN transition function expressing that a new state is given on the base of existing state and the occurrence of discrete events;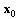 is the initial state vector of the PN.The transition function
is the initial state vector of the PN.The transition function 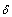 can be expressed by means of the linear discrete system
can be expressed by means of the linear discrete system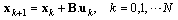 | (1) |
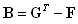 | (2) |
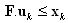 | (3) |
where k is the discrete step of the dynamics development;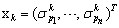 is the n-dimensional state vector;
is the n-dimensional state vector;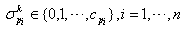 express the states of atomic activities by 0 (passivity) or by
express the states of atomic activities by 0 (passivity) or by 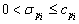 (activity);
(activity);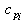 is the capacity of pi;
is the capacity of pi;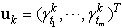 is the m-dimensional control vector;
is the m-dimensional control vector; 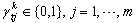 represent occurring of elementary discrete events (e.g. starting or ending the activities, failures, etc.) by 1 (presence of the corresponding discrete event) or by 0 (absence of the event); B, F, G are matrices of integers;
represent occurring of elementary discrete events (e.g. starting or ending the activities, failures, etc.) by 1 (presence of the corresponding discrete event) or by 0 (absence of the event); B, F, G are matrices of integers;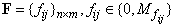 , expresses the causal relations among the states (as causes) and the discrete events occurring during the DES operation (as consequences) by 0 (nonexistence of the relation) or by
, expresses the causal relations among the states (as causes) and the discrete events occurring during the DES operation (as consequences) by 0 (nonexistence of the relation) or by 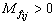 (existence and multiplicity of the relation);
(existence and multiplicity of the relation); 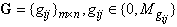 , expresess analogically to previous matrix the causal relations among the discrete events (as causes) and the DES states (as consequences); B is given according to (2);
, expresess analogically to previous matrix the causal relations among the discrete events (as causes) and the DES states (as consequences); B is given according to (2); 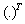 symbolizes the matrix or vector transposition.Just such an exact mathematical expression of P/T PN, in contrast to high-level PN, yields the possibility to deal with the cooperation synthesis in analytical terms. Developing (1) respecting (3) we have
symbolizes the matrix or vector transposition.Just such an exact mathematical expression of P/T PN, in contrast to high-level PN, yields the possibility to deal with the cooperation synthesis in analytical terms. Developing (1) respecting (3) we have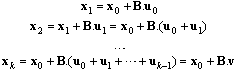 where
where 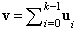 is named to be the Parikh's vector. It gives us information about how many times the particular transitions are fired during the development of the system dynamics from the initial state x0 to the state xk.Because not only the behaviour of agents but also the cooperation of agents exhibits attributes of DES we can utilize PN model for cooperating modules too.
is named to be the Parikh's vector. It gives us information about how many times the particular transitions are fired during the development of the system dynamics from the initial state x0 to the state xk.Because not only the behaviour of agents but also the cooperation of agents exhibits attributes of DES we can utilize PN model for cooperating modules too.
2. Modular Building DES
Having the PN models of DES modules we can think about building a DES structure from such modules. We can distinguish three kinds of interface among the agents. Namely, there are the interconnections throughout the PN transitions; the interconnections throughout the PN places; and the interconnections throughout both the PN transitions and the PN places.
2.1. Interface throughout the PN Transitions
In case of NA autonomous agents having the interface throughout the PN transitions the structural (incidence) matrices of the DES model have the following form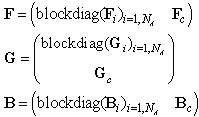 where
where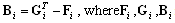 represent the matrices of parameters of the PN-based model of the module (agent) Ai, i = 1, 2, …, NA;
represent the matrices of parameters of the PN-based model of the module (agent) Ai, i = 1, 2, …, NA;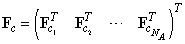 , where the entries represent the structure of the interface between cooperating agents, namely, interconnections from the agent places to interconnecting transitions;
, where the entries represent the structure of the interface between cooperating agents, namely, interconnections from the agent places to interconnecting transitions;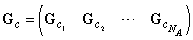 , where the entries represent the structure of the interface between cooperating agents, namely, interconnections from the interconnecting transitions to cooperating agents;
, where the entries represent the structure of the interface between cooperating agents, namely, interconnections from the interconnecting transitions to cooperating agents; 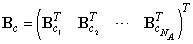 , where the entries are given as
, where the entries are given as 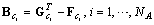 .This interface consists (exclusively) of additional PN transitions.
.This interface consists (exclusively) of additional PN transitions.
2.2. Interface Throughout the PN Places
Analogically, in case of the interface consisting (exclusively) of the additional PN places the structural (incidence) matrices are as follows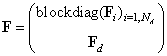
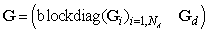
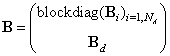 where
where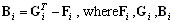 represent the matrices of parameters of the PN-based model of the module (agent) Ai, i = 1, 2, …, NA;
represent the matrices of parameters of the PN-based model of the module (agent) Ai, i = 1, 2, …, NA;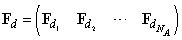 , where the entries represent the structure of the interface between cooperating agents, namely, interconnections from the agent places to interconnecting transitions;
, where the entries represent the structure of the interface between cooperating agents, namely, interconnections from the agent places to interconnecting transitions;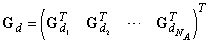 , where the entries represent the structure of the interface between cooperating agents, namely, interconnections from the interconnecting transitions to cooperating agents;
, where the entries represent the structure of the interface between cooperating agents, namely, interconnections from the interconnecting transitions to cooperating agents; 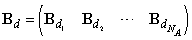 , where the entries are given as
, where the entries are given as 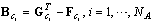 .This interface consists (exclusively) of additional PN places.
.This interface consists (exclusively) of additional PN places.
2.3. Interface through PN Transitions and PN Places
Both the PN transition and the PN places can be utilized in creating the interface between the agents. Then, the structural (incidence) matrices are the following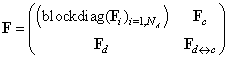
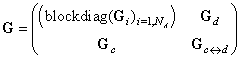
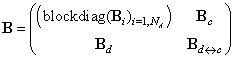 where the sense of the blocks is same than before, and moreover
where the sense of the blocks is same than before, and moreover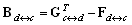 , where
, where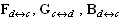 represent the relations among the transitions and places inside of the interface and vice versa.As we can see the matrices F, G, B acquire a special structure. Each of them has the big diagonal block describing the structure of autonomous agents and the specific part in the form of the letter L turned over the vertical axe. The blocks
represent the relations among the transitions and places inside of the interface and vice versa.As we can see the matrices F, G, B acquire a special structure. Each of them has the big diagonal block describing the structure of autonomous agents and the specific part in the form of the letter L turned over the vertical axe. The blocks 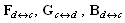 are situated in the diagonal just in the breakage of the turned L. These blocks represent a kernel of the interface and such a kernel can be understood to be another agent (coordinating the interface).
are situated in the diagonal just in the breakage of the turned L. These blocks represent a kernel of the interface and such a kernel can be understood to be another agent (coordinating the interface).
3. Supervision and Agent Cooperation
A supervisor for DES subsystems can be suitable in order to avoid the egoistic effort of autonomous agents, especially in case of limited sources (working space, raw materials or semi-products, energy, etc.). Namely, by means of prohibition some states of the global system describing the multi-agent system (MAS), e.g. like the so called mutex (mutual exclusion), a useless 'haggle' of agents each other for a priority can be removed on behalf of the global system purposes. However, on the contrary, the supervision process can be understood to be a carrier of the cooperation in the sense of the global system politics. In such a way the conditions for the supervisor synthesis represent the desired cooperation of agents in a group of agents or in MAS. In both cases some constraints has to be satisfied in order to achieve the desired behaviour (i.e. to synthesize the supervisor). Here, two kinds of constrains known from supervising methodology in DES control theory will be considered. Namely, (i) the constraints based on the P-invariants -[3]; (ii) the generalized constraints based not only on the PN laces but also on the PN Parikh's vector and/or on the PN transitions -[2,4].
4. Using PN Invariants at Supervision
The principle of the method is based on the PN P-invariants[3-5] being the vectors, v, with the property that multiplication of these vectors with any state vector 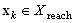 (i.e. reachable from a given initial state vector
(i.e. reachable from a given initial state vector 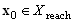 yields the same result (the relation of the state conservation), i.e.
yields the same result (the relation of the state conservation), i.e.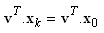 | (4) |
Because of (1) Hence, to satisfy the definition of P-invariants (4), the condition has to be met. P-invariants are useful in checking the property of mutual exclusion. To eliminate a selfish behaviour of autonomous agents at exploitation of limited joint resources it is necessary to allocate the sources to individual agents rightly, with respect to the global goal of MAS. Such a constraint of the agent behaviour and violation of their autonomy is rather in favour of MAS than in disfavour. In case of the existence of several (e.g. nx) invariants in a PN, the set of the P-invariants is created by the columns of the 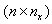 -dimensional matrix V being the solution of the homogeneous system of equations
-dimensional matrix V being the solution of the homogeneous system of equations 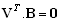 | (5) |
This equation represents the base for the supervisor synthesis method. Some additional PN places (slacks) can be added to the PN-model in question. The slacks create the places of the supervisor. Hence, (5) can be rewritten as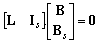 | (6) |
where,Is is 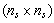 -dimensional identity matrix with being the number of slacks;L is
-dimensional identity matrix with being the number of slacks;L is 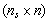 -dimensional matrix of integers representing (in a suitable form) the conditions imposed on marking of the original PN in the form
-dimensional matrix of integers representing (in a suitable form) the conditions imposed on marking of the original PN in the form | (7) |
whereb is the column vector of integers.Hence,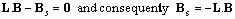 | (8) |
where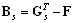 is the
is the 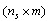 -dimensional matrix yielding (after its finding by computing) the structure of the PN-based model of the supervisor. Thus, the supervisor structure respects the actual structure of the matrix L. The supervised system (the group of autonomous agents augmented for the supervisor) is characterized by the augmented state vector xa and the augmented structural matrices as follows
-dimensional matrix yielding (after its finding by computing) the structure of the PN-based model of the supervisor. Thus, the supervisor structure respects the actual structure of the matrix L. The supervised system (the group of autonomous agents augmented for the supervisor) is characterized by the augmented state vector xa and the augmented structural matrices as follows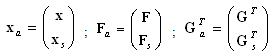 | (9) |
whereFs, Gs represent the structural (incidence) matrices of the supervisor. They correspond to the interconnections of the supervisor and autonomous agents.Analogically, the initial state of the supervisor sx0 can be computed as follows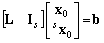 | (10) |
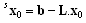 | (11) |
whereb is the integer vector of the corresponding dimensionality – i.e. 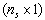 - given in (6) as the right side of the constraint imposed on the behaviour of the global system (i.e. cooperating agents). Its entries represent the limits for number of common tokens in the PN places occurring on the left side of (6). In other words, these entries represent the maximal admissible number of tokens that the corresponding PN places can possess (keep) altogether – i.e. to share them.
- given in (6) as the right side of the constraint imposed on the behaviour of the global system (i.e. cooperating agents). Its entries represent the limits for number of common tokens in the PN places occurring on the left side of (6). In other words, these entries represent the maximal admissible number of tokens that the corresponding PN places can possess (keep) altogether – i.e. to share them.
4.1. Example 1
Let us show how easy the dining philosophers problem defined by[1] can be solved by means of the supervisor synthesis. In computer science, this problem is an illustrative example of a common computing problem in concurrency. It is a classic multi-process synchronization problem where five computers competed for access to five shared tape drive peripherals. It was named as dining philosophers problem. Namely, five philosophers are sitting at a circular table with a large bowl of spaghetti in the centre doing one of two things - eating or thinking. While eating, they are not thinking, and while thinking, they are not eating. A fork (better a chopstick) is placed in between each philosopher. Each philosopher has one fork to his left and one fork to his right. It is assumed that a philosopher must eat with two forks. The philosopher can only use the fork on his immediate left or right.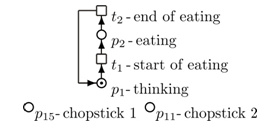 | Figure 1. The PN-based model of one philosopher activities. |
The PN-based model of the situation for one philosopher is given in Figure 1. In case of five philosophers the thinking is modelled by the PN places p1, p3, p5, p7, p9 and eating is represented by the places p2, p4, p6, p8, p10. In this situation all of the philosophers are thinking - p1, p3, p5, p7, p9 are active - i.e. no forks are necessary. However, formally they are expressed by means of the PN places p11, p12, p13, p14, p15 - see Figure 2, apart from interconnections. The defined problem can be solved by the supervisor synthesis method. The incidence matrices of the PN models of the autonomous agents Ai, i = 1, ..., 5 are 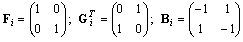 Consider that the initial states of the agents are the same
Consider that the initial states of the agents are the same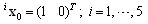 The parameters of the PN model of the group of autonomous agents can be expressed as follows
The parameters of the PN model of the group of autonomous agents can be expressed as follows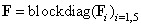
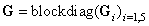
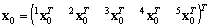 The conditions imposed on the autonomous agents are
The conditions imposed on the autonomous agents are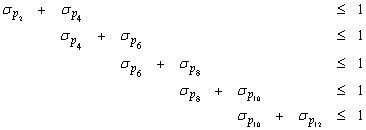 Verbally it means that two adjacent agents (neighbours) must not eat simultaneously. These conditions yield the matrix L and the vector b as follows
Verbally it means that two adjacent agents (neighbours) must not eat simultaneously. These conditions yield the matrix L and the vector b as follows Hence,
Hence,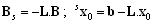
 Decomposing Bs we have structural matrices of the supervisor as follows
Decomposing Bs we have structural matrices of the supervisor as follows
 The structural matrices Fs, Gs of the supervisor give us the structural interconnections between the philosophers and the forks. Using the supervisor synthesis the problem was easily resolved. The PN-based model of the solution - the cooperating agents - is given in Figure 2.
The structural matrices Fs, Gs of the supervisor give us the structural interconnections between the philosophers and the forks. Using the supervisor synthesis the problem was easily resolved. The PN-based model of the solution - the cooperating agents - is given in Figure 2.
4.2. Example 2
Of course, the conditions for cooperation can be more complicated. Consider e.g. the group of 5 simple autonomous agents GrA = {A1, A2, A3, A4, A5} with the same structure like those handled above in Example 1. Of course, the agents need not be any philosophers but they can have a general keystone, where the state eating can mean ‘an activity’ and the state thinking can be e.g. ‘being idle’. Let us solve the situation when it is necessary to ensure that only one agent from the subgroup Sgr1 = {A1, A4, A5} and only one agent from the subgroup Sgr2 = {A2, A4, A5} and only one agent from the subgroup Sgr3 = {A3, A4, A5} can simultaneously cooperate with other agents from GrA. In other words, the agents inside the designated subgroups must not work simultaneously. Even, the agents A4 and A5 can work only individually (any cooperation with other agents is excluded). However, the agents A1, A2, A3 can work simultaneously. Now, the conditions prescribing the cooperation of agents are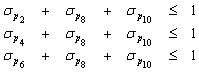 After the supervisor synthesis the PN model of the cooperating agents is displayed in Figure 3.
After the supervisor synthesis the PN model of the cooperating agents is displayed in Figure 3.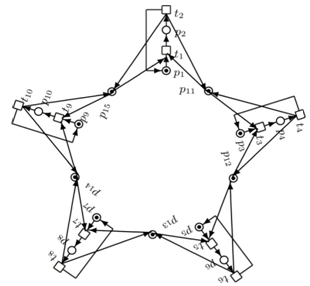 | Figure 2. The PN-based model of the supervised dining philosophers |
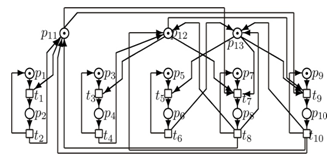 | Figure 3. The PN-based model of cooperating three groups of agents |
5. A More General Supervision
To widen a class of cooperation fashions the more general approach can be used. One of possibilities how to do this is to impose the conditions also on PN transitions. On this way also the Parikh's vector is very important and useful. The general linear constraints for supervisor synthesis were simply described in[2] as follows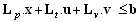 | (12) |
whereLp, Lt, Lv are, respectively, 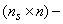 ,
, 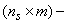 ,
, 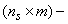 dimensional matrices. As it was shown in[2], when
dimensional matrices. As it was shown in[2], when 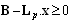 holds, the supervisor with the following structure and initial state
holds, the supervisor with the following structure and initial state 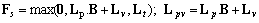
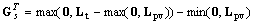
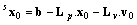 guarantees that the constraints are verified for the states resulting from the initial state. Here, the max(.) is the maximum operator for matrices. However, the maximum is taken element by element. Namely, in general, for the matrices X, Y, Z of the same dimensionality
guarantees that the constraints are verified for the states resulting from the initial state. Here, the max(.) is the maximum operator for matrices. However, the maximum is taken element by element. Namely, in general, for the matrices X, Y, Z of the same dimensionality , the relation Z = max(X, Y) it holds that zij = max(xij , yij ), i = 1, ..., n, j = 1,..., m. The same holds for min(.).
, the relation Z = max(X, Y) it holds that zij = max(xij , yij ), i = 1, ..., n, j = 1,..., m. The same holds for min(.).
5.1. Example 3 – A Case Study
The above introduced approach to the supervisor synthesis is applicable on very wide class of DES including agents, especially material agents in industry. To illustrate this let us apply the approach to the seemingly simple case, namely to the internal transport of flexible manufacturing system (FMS). Combining both kinds of constraints will be used step-by-step in order to synthesize the supervisor for the agents. The agents working in a common space - e.g. the tracks for AGVs (automatically guided vehicles) or mobile robots in a kind of FMS, or tracks for trains in a railways, etc. - have to be supervised in order to avoid a crash. To illustrate this, consider Nt tracks of AGVs in FMS. Denote them as agents Ai, i = 1,..., Nt. The AGVs carry semi-products from a place of FMS to another place and then they (empty or with another load) come round. In any track Ai there exist 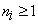 AGVs. Consider the tracks with AGVs to be the autonomous agents. The PN model of the single agent A1 is given in Figure 4. The parameters of the agents PN-based models are the following
AGVs. Consider the tracks with AGVs to be the autonomous agents. The PN model of the single agent A1 is given in Figure 4. The parameters of the agents PN-based models are the following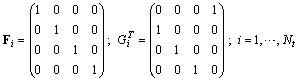
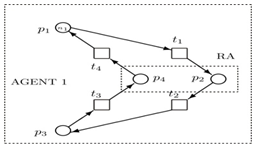 | Figure 4. The PN-based model of the agent. The places p2, p4 lie in the RA. |
During the agents activities n1 AGVs (represented by means of tokens situated in corresponding PN places) have to pass this track as well as a restricted area (RA) common for all agents, namely, even two times. RA is a “bottleneck” of the global system. Namely, in case of the AGVs e.g. the agent A1 passes RA: (i) when they carry some semi-products from a place p1 of FMS to another place p3 they have to pass the area (expressed by p2) first time, and (ii) when they come round to the place p1 they have to pass the same area (expressed now by p4) once more. However, because the space of the FMS where the agents operate is limited, there exists the restriction that only limited number of different AGVs, namely,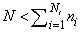 or often
or often 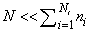 can operate in the RA simultaneously, the agents Ai have to be limited in their autonomous activities by a supervisor. The reason is that the agents themselves are not able to coalesce on a procedure satisfying all of them because the autonomous agents are usually egoistic (selfish). A violent driving of individual agents in RA might tend to wrecks with exterminatory effects, including some mechanical devastations, even standing the whole FMS off. Therefore, the supervisor determines a policy of the agents behaviour from the global point of view (i.e. conducive to the whole FMS) in order to achieve the satisfying results of the cooperative interactions among devices and expected behaviour (function) of the global FMS. Besides, it assures that no agent will be discriminated in its activities. The opposite view on the supervisor synthesis process can evoke an impress that such a process expresses e.g. the agents negotiation (although unwilling) or another kind of cooperation. Such a view is not so fantastic, because the supervisor does not drive its own selfish will or interest but its activity represents only the necessary part of the global strategy of the FMS behaviour, even the correct model of a part of the technological subprocess inside FMS. Another view on the supervisor synthesis process (especially from the control point of view) is that the supervisor realizes the objective function of the FMS subprocess. Namely, the supervisor only realizes the global demands on the behaviour of a part of FMS so as to meet the global aim of the whole FMS. In general, considering NA agents, we can describe the restrictions in analytical terms as follows
can operate in the RA simultaneously, the agents Ai have to be limited in their autonomous activities by a supervisor. The reason is that the agents themselves are not able to coalesce on a procedure satisfying all of them because the autonomous agents are usually egoistic (selfish). A violent driving of individual agents in RA might tend to wrecks with exterminatory effects, including some mechanical devastations, even standing the whole FMS off. Therefore, the supervisor determines a policy of the agents behaviour from the global point of view (i.e. conducive to the whole FMS) in order to achieve the satisfying results of the cooperative interactions among devices and expected behaviour (function) of the global FMS. Besides, it assures that no agent will be discriminated in its activities. The opposite view on the supervisor synthesis process can evoke an impress that such a process expresses e.g. the agents negotiation (although unwilling) or another kind of cooperation. Such a view is not so fantastic, because the supervisor does not drive its own selfish will or interest but its activity represents only the necessary part of the global strategy of the FMS behaviour, even the correct model of a part of the technological subprocess inside FMS. Another view on the supervisor synthesis process (especially from the control point of view) is that the supervisor realizes the objective function of the FMS subprocess. Namely, the supervisor only realizes the global demands on the behaviour of a part of FMS so as to meet the global aim of the whole FMS. In general, considering NA agents, we can describe the restrictions in analytical terms as follows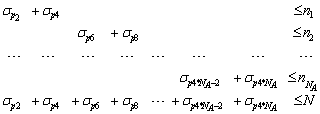 For illustration of such an approach, consider NA = 4, N = 2, n1 = n2 = n3 = n4 = 1. Consequently, we have
For illustration of such an approach, consider NA = 4, N = 2, n1 = n2 = n3 = n4 = 1. Consequently, we have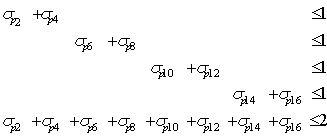 Thus, in the sense of[4], the supervisor can be synthesized as follows. Namely, from the above conditions is clear that
Thus, in the sense of[4], the supervisor can be synthesized as follows. Namely, from the above conditions is clear that
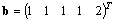 Consequently,
Consequently,
 When the initial state of the non-supervised agents is
When the initial state of the non-supervised agents is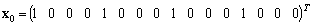 then
then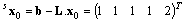 Having these parameters we can realize the supervisor structure. The structure of the supervised system is displayed in Figure 5.
Having these parameters we can realize the supervisor structure. The structure of the supervised system is displayed in Figure 5. 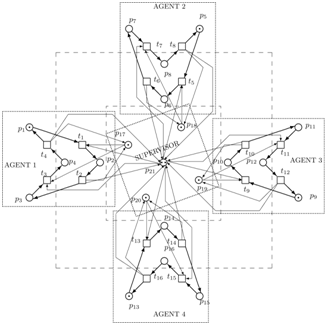 | Figure 5. The PN-based model of supervising 4 agents in order to simultaneously exploit the RA. |
The supervisor guarantees only fulfilling the prescribed restrictions. Therefore, the approach presented in[6,7] and more deeply described in[8-10], yielding the space of feasible trajectories can help to analyse the supervised plant as to the selection of the most suitable trajectories. In such a supervisor structure only the presence of N AGVs in the RA simultaneously is assured without designation which agents (in our example which N = 2 agents from four existing ones) have the priority to enter by their AGV into the area. To resolve this problem it is necessary to ensure priorities. Especially, in the given initial state, when all of the agents compete for entering the area, it is necessary to choice N of the Nt agents. During the global FMS dynamics development it is probable that not all of the agents will compete for entering. However, in general, also in such a case more than N agents can compete. Out of doubt, there is impossible in a real FMS to presume that the agents will negotiate each other to find the global optimum. Usually, there is no time for such a “democratic” negotiation process. However, there exists the way - we can synthesize another supervisor for the system being already supervised by the existing supervisor synthesized above. The advantage of such a multilevel approach consists in a flexibility. Namely, while the first level supervisor assures the stable situation that only two AGVs can occur in the RA, the second level can determine on which track (i.e. to which agent Ai AGVs belong in). In general, when we want to enter priorities, the new supervisor can be synthesized. We can consider e.g. that the priorities  of agents Ai descends with the ascending agent number - i.e.
of agents Ai descends with the ascending agent number - i.e.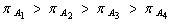 (but not only these ones, of course). The agent A1 has the highest priority as to entering to RA. The priorities of other agents descend with ascending number denoting the agent in question, namely in both directions - i.e. at carrying a part to the corresponding machine as well as on its regress. It means that the constraints imposed on elements of the Parikh's vector
(but not only these ones, of course). The agent A1 has the highest priority as to entering to RA. The priorities of other agents descend with ascending number denoting the agent in question, namely in both directions - i.e. at carrying a part to the corresponding machine as well as on its regress. It means that the constraints imposed on elements of the Parikh's vector 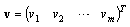 are, because m = 16, the following
are, because m = 16, the following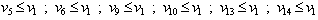
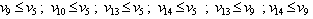 Considering v0 = 0 and respecting these constraints expressed in the light of (12) by b = 0 and Lv given as follows
Considering v0 = 0 and respecting these constraints expressed in the light of (12) by b = 0 and Lv given as follows we obtain the second supervisor with the structural matrices
we obtain the second supervisor with the structural matrices
 Hence, the initial state of the resulting supervised system is
Hence, the initial state of the resulting supervised system is 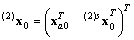 with
with 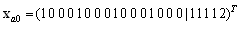 being the augmented state vector consisting of the state vector of autonomous agents and the state vector of the first supervisor and
being the augmented state vector consisting of the state vector of autonomous agents and the state vector of the first supervisor and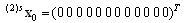 being the initial state of the second supervisor.Respecting the structure of the augmented system (i.e. the system supervised by the first supervisor), the structural matrices of the fully supervised system (i.e. by both supervisors) is the following
being the initial state of the second supervisor.Respecting the structure of the augmented system (i.e. the system supervised by the first supervisor), the structural matrices of the fully supervised system (i.e. by both supervisors) is the following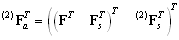
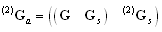
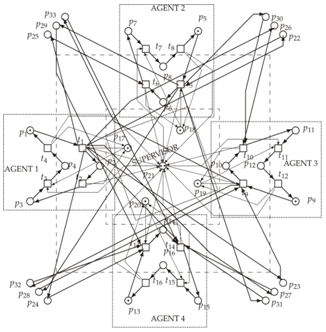 | Figure 6. The PN-based model of supervising 4 agents (AGVs) in order to simultaneously exploit the restricted area. |
Here, (2) (.) expresses that the matrices/vectors belonging to the second supervisor are meant. As it was already mentioned, the second supervisor is synthesized for the augmented system (i.e. for the original autonomous agents already supervised by the first supervisor). The structure of the second supervisor has to be embedded into the structure presented in Figure 5. The final augmented system (including the autonomous agents, first supervisor and the second one) is given in Figure 6. Here, the second supervisor is created by means of the PN places p22 – p33 together with the interconnecting arcs connecting these PN places with the previous structure given in Figure 5.
6. A Generalization of the Approach
The modular synthesis of the agent cooperation, especially that based on supervision, seems to be very hopeful. It makes possible to examine very deep and detailed mutual interferences of agents in a group to achieve a global aim. The approach need not include only two level supervision of the same group of agents. In general, the autonomous agents can be supervised on the first level by the first supervisor. This supervisor can be synthesized by virtue of (7) or (12). Afterwards, the supervisor on the second level can also be synthesized pursuant to (7) or (12), etc. Moreover, the second supervisor can be synthesized not only for the mentioned augmented system (i.e. autonomous agents supervised by the first supervisor) but also e.g. for two or more such augmented systems. Of course, here other levels of the supervisor synthesis can be applied too. This approach can continue in such a way ad lib. Consequently, the cooperation of an arbitrary structure of agents in a complicated hierarchical multi agent system can be achieved.
7. Conclusions
The paper has pointed out the possibility of the agent cooperation synthesis by means of supervision well known in DES control theory. The agents are modelled by means of P/T PN. The principles of supervision methods utilized in P/T PN theory are used. By means of supervision the demands on the expected collective behaviour of autonomous agents are forced in order to avoid a possible egoism of the agents. The modularity approach proposed here represents an effective help on that way. Two kinds of supervision were utilized – those ones based on P-invariants of P/T PN and on more general approach defined first time in[2]. Three kinds of modularity were proposed – those ones based on PN transitions, on PN places and on their combination. The applicability of the approach was illustrated on examples.
ACKNOWLEDGEMENTS
The research was partially supported by the Slovak Grant Agency for Sciences VEGA under grant # 2/0075/09. The author cordially thanks VEGA for the support.
References
| [1] | E. W. Dijkstra, 1971, “Hierarchical ordering of sequential processes”, Acta Informatica, 1, 115-138 |
| [2] | M. V. Iordache, “Methods for the supervisory control of concurrent systems based on Petri nets abstraction”, PhD dissertation, University of Notre Dame, Notre Dame, Indiana, USA, 2003 |
| [3] | M. V. Iordache and P. J. Antsaklis, 2006, “Supervision based on place invariants: A survey”, Discrete Event Dynamic Systems, 16(4), 451-492 |
| [4] | M. V. Iordache and P. J. Antsaklis, 2006, Supervisory Control of Concurrent Systems: A Petri Net Structural Approach, Birkhauser, Boston |
| [5] | T. Murata, 1989, “Petri nets: Properties, analysis and applications”, Proceedings of the IEEE, 77(4), 541-580 |
| [6] | F. Capkovic, 2007, “Modelling, analyzing and control of interactions among agents in MAS”, Computing and Informatics, 26(5), 507-541 |
| [7] | F. Capkovic, DES control synthesis and cooperation of agents, In N. T. Nguyen, R. Kowalczyk, and Shyi-Ming Chen, editors, Computational Collective Intelligence, ser. Lecture Notes in Artificial Intelligence (LNAI), Berlin-Heidelberg, Germany: Springer, 2009, vol. 5796, pp. 596-607 |
| [8] | F. Capkovic, 2010, “Automatic control synthesis for agents and their cooperation in MAS”, Computing and Informatics, 29(6+), pp. 1045-1071 |
| [9] | F. Capkovic, Cooperation of hybrid agents in models of manufacturing systems, In J. O'Shea, N. T. Nguyen, K. Crockett, R. J. Howlett and C. J. Lakhmi, editors, Agent and Multi-Agent Systems: Technologies and Applications, ser. Lecture Notes in Artificial Intelligence (LNAI), Berlin-Heidelberg, Germany: Springer, 2011, vol. 6682, pp. 221-230 |
| [10] | F. Capkovic, Modelling of Agents Cooperation and Negotiation. In P. Jedrzejowicz, N.T. Nguyen and Kiem Hoang, editors, Computational Collective Intelligence - Technologies and Applications, ser. Lecture Notes in Artificial Intelligence (LNAI), Berlin-Heidelberg, Germany: Springer, 2011, vol. 6923, pp. 110-119 |

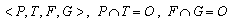 whereP is the set of the PN places pi , i = 1, 2, …, n;T is the set of the PN transitions tj, j = 1, 2, …, m;
whereP is the set of the PN places pi , i = 1, 2, …, n;T is the set of the PN transitions tj, j = 1, 2, …, m;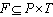 is the set of edges from places to transitions;
is the set of edges from places to transitions;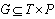 is the set of edges from transitions to places;O is the empty set.However, PN have also their dynamics. It is formally given by the following quadrupletThe system form of the PN-based model of a DES modu-le is
is the set of edges from transitions to places;O is the empty set.However, PN have also their dynamics. It is formally given by the following quadrupletThe system form of the PN-based model of a DES modu-le is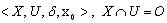 where X is the set of the PN state vectors
where X is the set of the PN state vectors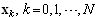 ;U is the set of the control vectors
;U is the set of the control vectors 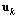 of the PN, where
of the PN, where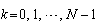 ;
;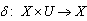 is the PN transition function expressing that a new state is given on the base of existing state and the occurrence of discrete events;
is the PN transition function expressing that a new state is given on the base of existing state and the occurrence of discrete events;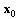 is the initial state vector of the PN.The transition function
is the initial state vector of the PN.The transition function 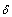 can be expressed by means of the linear discrete system
can be expressed by means of the linear discrete system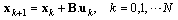
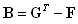
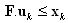
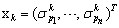 is the n-dimensional state vector;
is the n-dimensional state vector;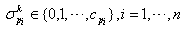 express the states of atomic activities by 0 (passivity) or by
express the states of atomic activities by 0 (passivity) or by 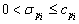 (activity);
(activity);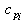 is the capacity of pi;
is the capacity of pi;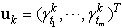 is the m-dimensional control vector;
is the m-dimensional control vector; 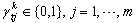 represent occurring of elementary discrete events (e.g. starting or ending the activities, failures, etc.) by 1 (presence of the corresponding discrete event) or by 0 (absence of the event); B, F, G are matrices of integers;
represent occurring of elementary discrete events (e.g. starting or ending the activities, failures, etc.) by 1 (presence of the corresponding discrete event) or by 0 (absence of the event); B, F, G are matrices of integers;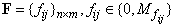 , expresses the causal relations among the states (as causes) and the discrete events occurring during the DES operation (as consequences) by 0 (nonexistence of the relation) or by
, expresses the causal relations among the states (as causes) and the discrete events occurring during the DES operation (as consequences) by 0 (nonexistence of the relation) or by 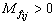 (existence and multiplicity of the relation);
(existence and multiplicity of the relation); 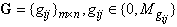 , expresess analogically to previous matrix the causal relations among the discrete events (as causes) and the DES states (as consequences); B is given according to (2);
, expresess analogically to previous matrix the causal relations among the discrete events (as causes) and the DES states (as consequences); B is given according to (2); 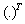 symbolizes the matrix or vector transposition.Just such an exact mathematical expression of P/T PN, in contrast to high-level PN, yields the possibility to deal with the cooperation synthesis in analytical terms. Developing (1) respecting (3) we have
symbolizes the matrix or vector transposition.Just such an exact mathematical expression of P/T PN, in contrast to high-level PN, yields the possibility to deal with the cooperation synthesis in analytical terms. Developing (1) respecting (3) we have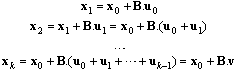 where
where 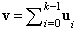 is named to be the Parikh's vector. It gives us information about how many times the particular transitions are fired during the development of the system dynamics from the initial state x0 to the state xk.Because not only the behaviour of agents but also the cooperation of agents exhibits attributes of DES we can utilize PN model for cooperating modules too.
is named to be the Parikh's vector. It gives us information about how many times the particular transitions are fired during the development of the system dynamics from the initial state x0 to the state xk.Because not only the behaviour of agents but also the cooperation of agents exhibits attributes of DES we can utilize PN model for cooperating modules too.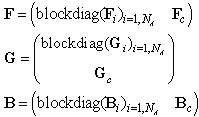 where
where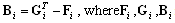 represent the matrices of parameters of the PN-based model of the module (agent) Ai, i = 1, 2, …, NA;
represent the matrices of parameters of the PN-based model of the module (agent) Ai, i = 1, 2, …, NA;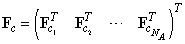 , where the entries represent the structure of the interface between cooperating agents, namely, interconnections from the agent places to interconnecting transitions;
, where the entries represent the structure of the interface between cooperating agents, namely, interconnections from the agent places to interconnecting transitions;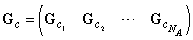 , where the entries represent the structure of the interface between cooperating agents, namely, interconnections from the interconnecting transitions to cooperating agents;
, where the entries represent the structure of the interface between cooperating agents, namely, interconnections from the interconnecting transitions to cooperating agents; 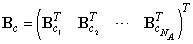 , where the entries are given as
, where the entries are given as 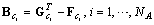 .This interface consists (exclusively) of additional PN transitions.
.This interface consists (exclusively) of additional PN transitions. 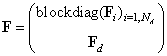
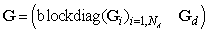
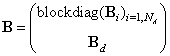 where
where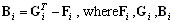 represent the matrices of parameters of the PN-based model of the module (agent) Ai, i = 1, 2, …, NA;
represent the matrices of parameters of the PN-based model of the module (agent) Ai, i = 1, 2, …, NA;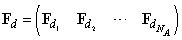 , where the entries represent the structure of the interface between cooperating agents, namely, interconnections from the agent places to interconnecting transitions;
, where the entries represent the structure of the interface between cooperating agents, namely, interconnections from the agent places to interconnecting transitions;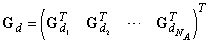 , where the entries represent the structure of the interface between cooperating agents, namely, interconnections from the interconnecting transitions to cooperating agents;
, where the entries represent the structure of the interface between cooperating agents, namely, interconnections from the interconnecting transitions to cooperating agents; 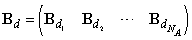 , where the entries are given as
, where the entries are given as 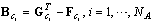 .This interface consists (exclusively) of additional PN places.
.This interface consists (exclusively) of additional PN places.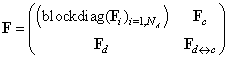
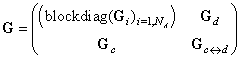
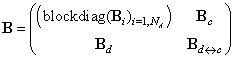 where the sense of the blocks is same than before, and moreover
where the sense of the blocks is same than before, and moreover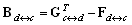 , where
, where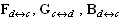 represent the relations among the transitions and places inside of the interface and vice versa.As we can see the matrices F, G, B acquire a special structure. Each of them has the big diagonal block describing the structure of autonomous agents and the specific part in the form of the letter L turned over the vertical axe. The blocks
represent the relations among the transitions and places inside of the interface and vice versa.As we can see the matrices F, G, B acquire a special structure. Each of them has the big diagonal block describing the structure of autonomous agents and the specific part in the form of the letter L turned over the vertical axe. The blocks 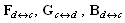 are situated in the diagonal just in the breakage of the turned L. These blocks represent a kernel of the interface and such a kernel can be understood to be another agent (coordinating the interface).
are situated in the diagonal just in the breakage of the turned L. These blocks represent a kernel of the interface and such a kernel can be understood to be another agent (coordinating the interface). 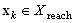 (i.e. reachable from a given initial state vector
(i.e. reachable from a given initial state vector 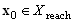 yields the same result (the relation of the state conservation), i.e.
yields the same result (the relation of the state conservation), i.e.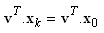
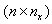 -dimensional matrix V being the solution of the homogeneous system of equations
-dimensional matrix V being the solution of the homogeneous system of equations 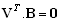
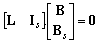
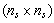 -dimensional identity matrix with being the number of slacks;L is
-dimensional identity matrix with being the number of slacks;L is 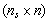 -dimensional matrix of integers representing (in a suitable form) the conditions imposed on marking of the original PN in the form
-dimensional matrix of integers representing (in a suitable form) the conditions imposed on marking of the original PN in the form
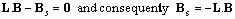
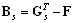 is the
is the 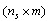 -dimensional matrix yielding (after its finding by computing) the structure of the PN-based model of the supervisor. Thus, the supervisor structure respects the actual structure of the matrix L. The supervised system (the group of autonomous agents augmented for the supervisor) is characterized by the augmented state vector xa and the augmented structural matrices as follows
-dimensional matrix yielding (after its finding by computing) the structure of the PN-based model of the supervisor. Thus, the supervisor structure respects the actual structure of the matrix L. The supervised system (the group of autonomous agents augmented for the supervisor) is characterized by the augmented state vector xa and the augmented structural matrices as follows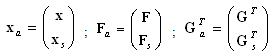
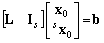
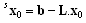
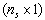 - given in (6) as the right side of the constraint imposed on the behaviour of the global system (i.e. cooperating agents). Its entries represent the limits for number of common tokens in the PN places occurring on the left side of (6). In other words, these entries represent the maximal admissible number of tokens that the corresponding PN places can possess (keep) altogether – i.e. to share them.
- given in (6) as the right side of the constraint imposed on the behaviour of the global system (i.e. cooperating agents). Its entries represent the limits for number of common tokens in the PN places occurring on the left side of (6). In other words, these entries represent the maximal admissible number of tokens that the corresponding PN places can possess (keep) altogether – i.e. to share them.
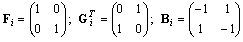 Consider that the initial states of the agents are the same
Consider that the initial states of the agents are the same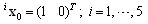 The parameters of the PN model of the group of autonomous agents can be expressed as follows
The parameters of the PN model of the group of autonomous agents can be expressed as follows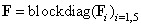
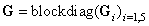
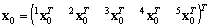 The conditions imposed on the autonomous agents are
The conditions imposed on the autonomous agents are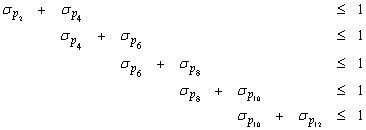 Verbally it means that two adjacent agents (neighbours) must not eat simultaneously. These conditions yield the matrix L and the vector b as follows
Verbally it means that two adjacent agents (neighbours) must not eat simultaneously. These conditions yield the matrix L and the vector b as follows Hence,
Hence,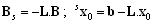
 Decomposing Bs we have structural matrices of the supervisor as follows
Decomposing Bs we have structural matrices of the supervisor as follows
 The structural matrices Fs, Gs of the supervisor give us the structural interconnections between the philosophers and the forks. Using the supervisor synthesis the problem was easily resolved. The PN-based model of the solution - the cooperating agents - is given in Figure 2.
The structural matrices Fs, Gs of the supervisor give us the structural interconnections between the philosophers and the forks. Using the supervisor synthesis the problem was easily resolved. The PN-based model of the solution - the cooperating agents - is given in Figure 2. 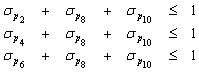 After the supervisor synthesis the PN model of the cooperating agents is displayed in Figure 3.
After the supervisor synthesis the PN model of the cooperating agents is displayed in Figure 3.

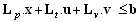
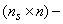 ,
, 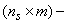 ,
, 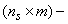 dimensional matrices. As it was shown in[2], when
dimensional matrices. As it was shown in[2], when 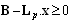 holds, the supervisor with the following structure and initial state
holds, the supervisor with the following structure and initial state 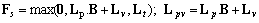
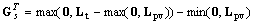
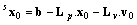 guarantees that the constraints are verified for the states resulting from the initial state. Here, the max(.) is the maximum operator for matrices. However, the maximum is taken element by element. Namely, in general, for the matrices X, Y, Z of the same dimensionality
guarantees that the constraints are verified for the states resulting from the initial state. Here, the max(.) is the maximum operator for matrices. However, the maximum is taken element by element. Namely, in general, for the matrices X, Y, Z of the same dimensionality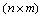 , the relation Z = max(X, Y) it holds that zij = max(xij , yij ), i = 1, ..., n, j = 1,..., m. The same holds for min(.).
, the relation Z = max(X, Y) it holds that zij = max(xij , yij ), i = 1, ..., n, j = 1,..., m. The same holds for min(.).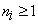 AGVs. Consider the tracks with AGVs to be the autonomous agents. The PN model of the single agent A1 is given in Figure 4. The parameters of the agents PN-based models are the following
AGVs. Consider the tracks with AGVs to be the autonomous agents. The PN model of the single agent A1 is given in Figure 4. The parameters of the agents PN-based models are the following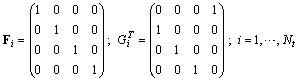

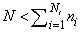 or often
or often 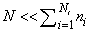 can operate in the RA simultaneously, the agents Ai have to be limited in their autonomous activities by a supervisor. The reason is that the agents themselves are not able to coalesce on a procedure satisfying all of them because the autonomous agents are usually egoistic (selfish). A violent driving of individual agents in RA might tend to wrecks with exterminatory effects, including some mechanical devastations, even standing the whole FMS off. Therefore, the supervisor determines a policy of the agents behaviour from the global point of view (i.e. conducive to the whole FMS) in order to achieve the satisfying results of the cooperative interactions among devices and expected behaviour (function) of the global FMS. Besides, it assures that no agent will be discriminated in its activities. The opposite view on the supervisor synthesis process can evoke an impress that such a process expresses e.g. the agents negotiation (although unwilling) or another kind of cooperation. Such a view is not so fantastic, because the supervisor does not drive its own selfish will or interest but its activity represents only the necessary part of the global strategy of the FMS behaviour, even the correct model of a part of the technological subprocess inside FMS. Another view on the supervisor synthesis process (especially from the control point of view) is that the supervisor realizes the objective function of the FMS subprocess. Namely, the supervisor only realizes the global demands on the behaviour of a part of FMS so as to meet the global aim of the whole FMS. In general, considering NA agents, we can describe the restrictions in analytical terms as follows
can operate in the RA simultaneously, the agents Ai have to be limited in their autonomous activities by a supervisor. The reason is that the agents themselves are not able to coalesce on a procedure satisfying all of them because the autonomous agents are usually egoistic (selfish). A violent driving of individual agents in RA might tend to wrecks with exterminatory effects, including some mechanical devastations, even standing the whole FMS off. Therefore, the supervisor determines a policy of the agents behaviour from the global point of view (i.e. conducive to the whole FMS) in order to achieve the satisfying results of the cooperative interactions among devices and expected behaviour (function) of the global FMS. Besides, it assures that no agent will be discriminated in its activities. The opposite view on the supervisor synthesis process can evoke an impress that such a process expresses e.g. the agents negotiation (although unwilling) or another kind of cooperation. Such a view is not so fantastic, because the supervisor does not drive its own selfish will or interest but its activity represents only the necessary part of the global strategy of the FMS behaviour, even the correct model of a part of the technological subprocess inside FMS. Another view on the supervisor synthesis process (especially from the control point of view) is that the supervisor realizes the objective function of the FMS subprocess. Namely, the supervisor only realizes the global demands on the behaviour of a part of FMS so as to meet the global aim of the whole FMS. In general, considering NA agents, we can describe the restrictions in analytical terms as follows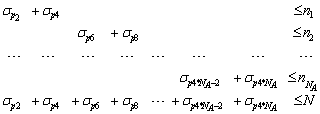 For illustration of such an approach, consider NA = 4, N = 2, n1 = n2 = n3 = n4 = 1. Consequently, we have
For illustration of such an approach, consider NA = 4, N = 2, n1 = n2 = n3 = n4 = 1. Consequently, we have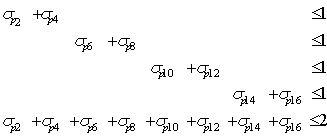 Thus, in the sense of[4], the supervisor can be synthesized as follows. Namely, from the above conditions is clear that
Thus, in the sense of[4], the supervisor can be synthesized as follows. Namely, from the above conditions is clear that
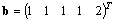 Consequently,
Consequently,
 When the initial state of the non-supervised agents is
When the initial state of the non-supervised agents is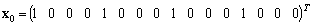 then
then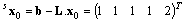 Having these parameters we can realize the supervisor structure. The structure of the supervised system is displayed in Figure 5.
Having these parameters we can realize the supervisor structure. The structure of the supervised system is displayed in Figure 5. 
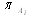 of agents Ai descends with the ascending agent number - i.e.
of agents Ai descends with the ascending agent number - i.e.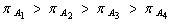 (but not only these ones, of course). The agent A1 has the highest priority as to entering to RA. The priorities of other agents descend with ascending number denoting the agent in question, namely in both directions - i.e. at carrying a part to the corresponding machine as well as on its regress. It means that the constraints imposed on elements of the Parikh's vector
(but not only these ones, of course). The agent A1 has the highest priority as to entering to RA. The priorities of other agents descend with ascending number denoting the agent in question, namely in both directions - i.e. at carrying a part to the corresponding machine as well as on its regress. It means that the constraints imposed on elements of the Parikh's vector 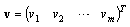 are, because m = 16, the following
are, because m = 16, the following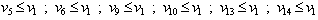
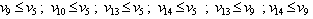 Considering v0 = 0 and respecting these constraints expressed in the light of (12) by b = 0 and Lv given as follows
Considering v0 = 0 and respecting these constraints expressed in the light of (12) by b = 0 and Lv given as follows we obtain the second supervisor with the structural matrices
we obtain the second supervisor with the structural matrices
 Hence, the initial state of the resulting supervised system is
Hence, the initial state of the resulting supervised system is 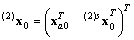 with
with 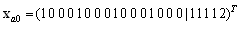 being the augmented state vector consisting of the state vector of autonomous agents and the state vector of the first supervisor and
being the augmented state vector consisting of the state vector of autonomous agents and the state vector of the first supervisor and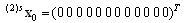 being the initial state of the second supervisor.Respecting the structure of the augmented system (i.e. the system supervised by the first supervisor), the structural matrices of the fully supervised system (i.e. by both supervisors) is the following
being the initial state of the second supervisor.Respecting the structure of the augmented system (i.e. the system supervised by the first supervisor), the structural matrices of the fully supervised system (i.e. by both supervisors) is the following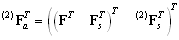
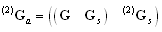

 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML