-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Hydraulic Engineering
p-ISSN: 2169-9771 e-ISSN: 2169-9801
2025; 13(1): 1-16
doi:10.5923/j.ijhe.20251301.01
Received: Sep. 18, 2025; Accepted: Oct. 3, 2025; Published: Oct. 10, 2025

Developing an Optimization Model for Pumping Operations in a Water Supply System in Brazil
Angélica Luciana Barros de Campos1, Diogo Valadão de Brito Gebrim2, Welitom Ttatom Pereira da Silva3, Sergio Koide4
1Inspection Division of the State of Mato Grosso, Brazilian National Mining Agency, Cuiabá, Brazil
2Water Production Superintendence, Environmental Sanitation Company of the Federal District, Brasília, Brazil
3Department of Sanitary and Environmental Engineering, Federal University of Mato Grosso, Cuiabá, Brazil
4Department of Civil and Environmental Engineering, University of Brasília, Brasília, Brazil
Correspondence to: Angélica Luciana Barros de Campos, Inspection Division of the State of Mato Grosso, Brazilian National Mining Agency, Cuiabá, Brazil.
| Email: |  |
Copyright © 2025 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Electricity consumption in public water supply systems is one of the main components of operational costs and is strongly influenced by the adopted operating strategies. In this study, an optimization model was developed by integrating computational algorithms that use artificial intelligence with the EPANET 2.0 software, aiming to reduce electricity costs associated with pumping in the Descoberto River Water Production System, which supplies water to approximately 60% of the population of the Federal District, Brazil. The proposed methodology incorporated Fuzzy penalties and processing time reduction techniques, aiming to make the model applicable to real and highly complex systems. The results obtained demonstrated that the model is effective in identifying operational rules that lead to the minimization of energy costs. However, it was observed that, in certain situations, the excessive number of pump and valve activations may limit the applicability of the proposed solutions due to the potential impact on equipment durability. It can be concluded that the model has strong potential as a decision-support tool, and is capable of validating previously defined operational strategies and simulating system behavior under different operating scenarios. The application in a real environment will depend on implementing additional adjustments, including limiting the number of activations, real-time demand forecasting, and integration of complementary subsystems.
Keywords: Water supply, Operational optimization, Artificial intelligence, Descoberto Water Production System
Cite this paper: Angélica Luciana Barros de Campos, Diogo Valadão de Brito Gebrim, Welitom Ttatom Pereira da Silva, Sergio Koide, Developing an Optimization Model for Pumping Operations in a Water Supply System in Brazil, International Journal of Hydraulic Engineering, Vol. 13 No. 1, 2025, pp. 1-16. doi: 10.5923/j.ijhe.20251301.01.
Article Outline
1. Introduction
- The growing importance of sustainable development and the increase in environmental awareness within society have driven organizations across various economic sectors to pursue more efficient energy management [1]. Despite the global concern with energy efficiency, in the Brazilian context, the evolution of energy management practices has progressed slowly in most municipalities, mainly due to low investments in maintenance and modernization of control systems. However, in the Federal District, the Environmental Sanitation Company of the Federal District (CAESB) has allocated significant resources to modernizing its operational systems and adopting clean energy sources. In the medium term, these initiatives will enable the implementation of real-time automated and optimized control systems, while also helping to reduce operational costs associated with electricity consumption.In 2022, the Brazilian sanitation sector consumed approximately 12.61 billion kWh of electricity for water supply and 1.72 billion kWh for wastewater services, resulting in expenses of about 9.25 billion Brazilian reais (BRL) [2]. Most of this consumption is attributed to pumping stations. At CAESB, electricity expenses are the second-largest operational cost component. In 2023, the company’s consumption reached around 290.65 million kWh, at a cost exceeding 190 million Brazilian reais (BRL).Several authors have pointed out, for decades, that energy consumption in most water supply systems could be reduced if appropriate optimization methods were applied [3]. According to these studies, improvements in hydraulic and energy aspects could lead to savings of at least 10% in energy consumption. In recent years, the application of optimization algorithms in water distribution systems has intensified, particularly focusing on methods such as the Genetic Algorithm [4,5,6], Harmony Search [7,8], Particle Swarm Optimization [9,10], Ant Colony Optimization [11], Discrete Dynamically Dimensioned Search (DDDS) [12], and Differential Evolution [13].Most of these studies adopt reference systems from the literature, which are simpler and have fewer operational units, such as those presented by [14] and [15], either to enable performance comparison between algorithms or due to the unavailability of data required for modeling real systems. Unlike these approaches, the present study applies a real and highly complex Water Supply System (WSS), similar to the one in Vasan [16].The system under study, called the Descoberto River System, located in the Federal District, is the largest production system in the region in terms of production capacity and population served. Its main operational units include: water intake from the Descoberto River, the Raw Water Pumping Station, the Descoberto Water Treatment Plant (WTP), fifteen ground storage tanks, six elevated reservoirs, seven treated water pumping stations, and nine booster stations. Therefore, it is a highly complex system, both in terms of scale and the number of operational units, which adds further challenges to the optimization process.Optimization algorithms are generally applied together with hydraulic models, such as EPANET 2.0, to simulate and optimize WSS operations [6,17]. However, traditional hydraulic simulators, such as EPANET 2.0, present high computational processing times, which can make their application to real operations unfeasible, especially in excessively detailed networks. As an alternative, skeletonized or simplified models are used [18], which reduce computational complexity without significantly impairing simulation accuracy.Due to the complexity of WSS operation optimization, it is also common to apply the Penalty Method, which penalizes infeasible solutions, guides the search toward the feasible solution space, and transforms constrained optimization problems into unconstrained ones by applying penalty coefficients [8,17,19]. Among the strategies adopted by some authors, the so-called “death penalty” stands out, in which solutions that violate constraints receive constant penalties. However, this approach has limitations, as infeasible individuals in the initial population, which would otherwise be discarded, may be essential for obtaining optimized solutions [17].In this context, Fuzzy logic–based penalties [15] emerge as a promising alternative [20], as they enable different degrees of penalization for each type of constraint violation, providing greater flexibility and efficiency of the optimization process.Thus, this study aims to primarily develop an optimization model that defines operational rules and minimizes electricity costs in water pumping, using Fuzzy penalties and computational processing time reduction techniques, based on the case study of the Descoberto River System. This study is particularly relevant in the current Brazilian context, marked by low rainfall rates and critical reservoir levels, which have resulted in increased energy costs and directly impacted the tariffs charged to consumers.
2. Methodology
2.1. Characterization of the Descoberto Water Production System
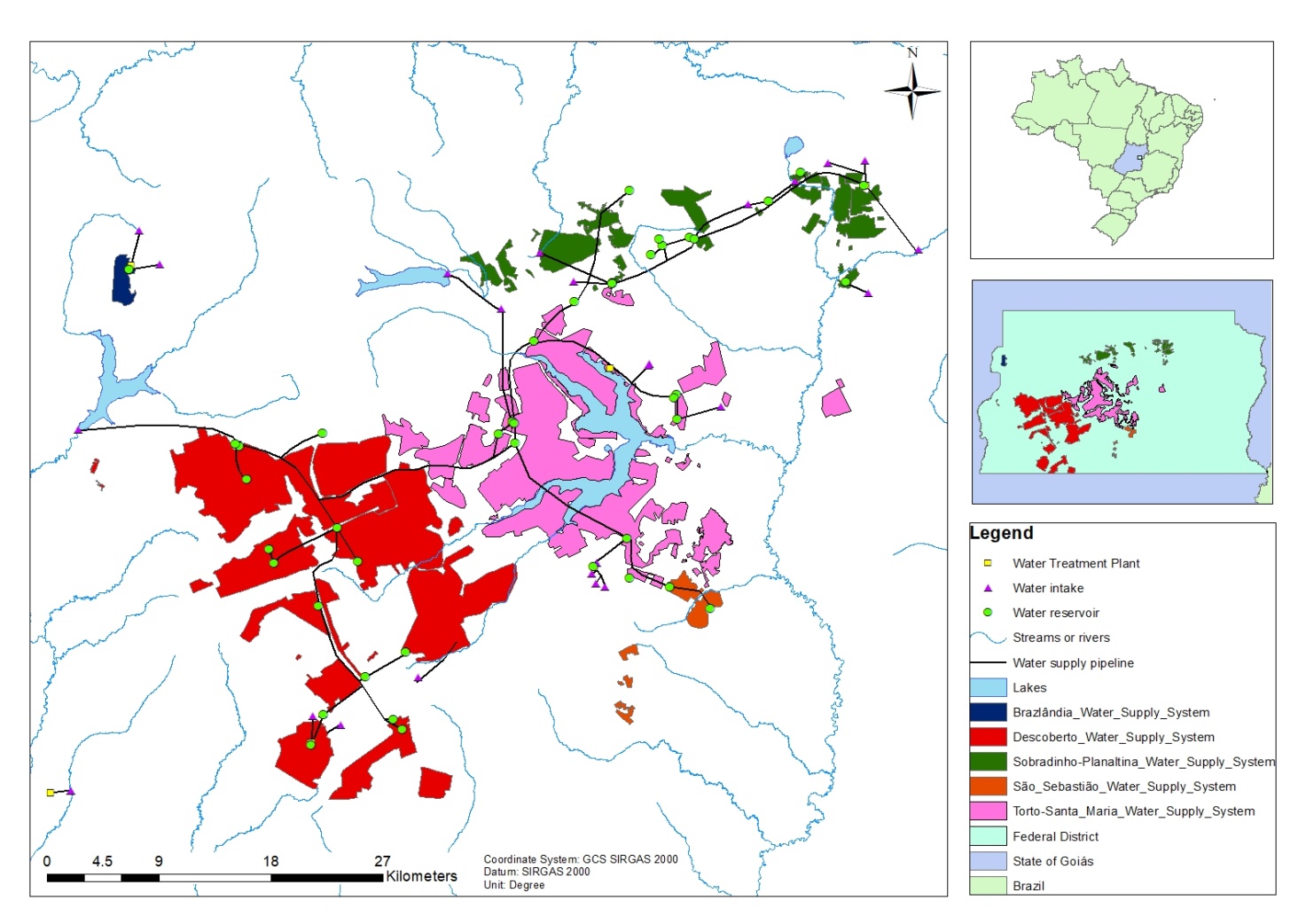
- According to CAESB [21], the Water Production System for Urban Supply of the Federal District (SPA) comprises the Descoberto, Corumbá, Torto/Santa Maria/Bananal, Paranoá Lake, Sobradinho/Planaltina, Jardim Botânico/São Sebastião, Brazlândia, Água Quente, Engenho das Lages, Incra 8, Papuda, and Vale do Amanhecer systems. Inaugurated in 2022, the Corumbá system expanded the service areas and increased the company’s potable water production capacity by approximately 15%. Some of these water supply systems are shown in Figure 1.
 | Figure 1. Federal District Water Production Systems |
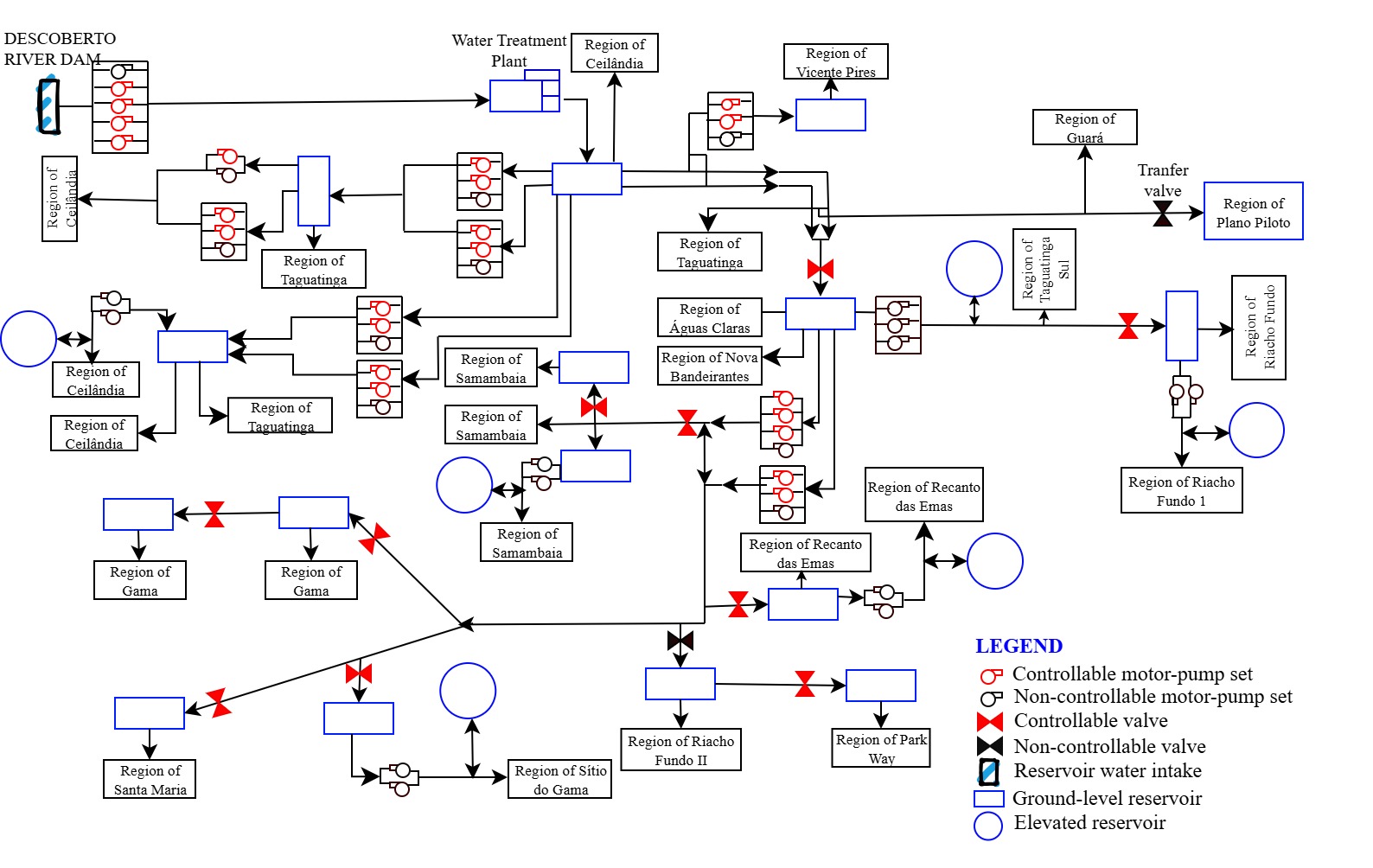 | Figure 2. Conveyance flowchart of the Descoberto Water Supply System |
2.2. Optimization Model
- The optimization model was developed based on a representation of the Descoberto Water Supply System, comprising reservoirs, pumps, and valves, considering a deterministic water consumption regime. The program simulates the operation of a typical day of the system over a 24-hour horizon (from 0:00 to 24:00), aiming to minimize the operational costs of the pumps with hourly resolution. The optimization aims to meet demand without supply failures while respecting operational constraints, such as minimum and maximum reservoir levels, maximum number of pump activations, positive pressure at demand nodes, and the difference between initial and final reservoir levels, all within pre-established limits.Similarly to Li [6], who proposed optimizing pumping station design to address insufficient pressure issues during peak hours at a railway station and in a municipal committee area, this study adopted a hydraulic modeling–based approach. The authors built a network model, conducted a systematic analysis of the supply system, and applied the NSGA-III algorithm in conjunction with EPANET software to solve a multi-objective optimization problem, simultaneously considering energy consumption and water age in the network, as well as hydraulic constraints such as reservoir levels and node pressures.In the present study, the methodological basis was the algorithm developed by Gebrim [22], which uses a Simple Genetic Algorithm implemented via the GALib library from the Massachusetts Institute of Technology (MIT), coupled with the EPANET 2.0 hydraulic simulator [24], using the codes available in the Toolkit Library. The adopted methodology also follows the line of research developed by [5,15,25]. The algorithm was implemented in C++ programming language using the Microsoft Visual Studio Express 2012 compiler.The optimization modeling aims to minimize the electricity costs associated with system pumping, as addressed in studies such as [6,26,27]. The objective function considers the total daily electricity cost, including both the energy consumed by the pumps and the demand cost of the consumer units, in accordance with the blue and green time-of-use tariffs, which differentiate between peak and off-peak periods.The total electricity cost used in pumping is represented by the objective function (Equation 1), consisting of the sum of the pump consumption costs and the demand cost, the latter divided by 30 to represent the daily value. The demand cost is calculated based on the highest power demanded by each consumer unit during each tariff period of the day (peak and off-peak hours).
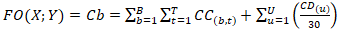 | (1) |
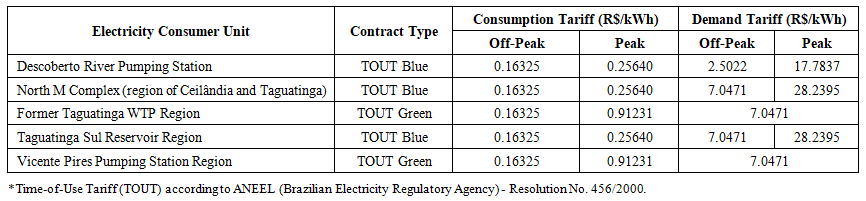 | Table 1. Electricity tariff by pumping station analyzed |
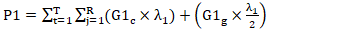 | (2) |
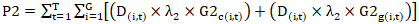 | (3) |
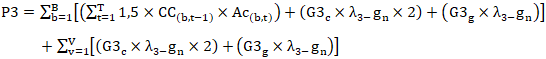 | (4) |
|
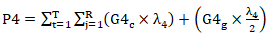 | (5) |
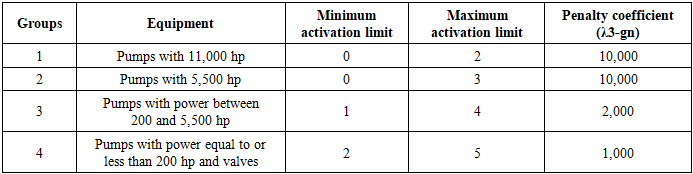
2.3. Application of the Fuzzy Approach to Penalties
- In the model proposed by [22], the penalization strategy used the so-called “death penalty,” which could result in the loss of individuals that would contribute to improving the optimized solution. This approach could lead to the elimination of promising solutions, preventing progress toward optimization. Considering that the way the fitness function is penalized directly and significantly influences the search for optimized solutions, a new penalization strategy was implemented. This new approach is based on the methodology proposed by [7,15,20], using Fuzzy logic for the formulation of penalization equations, by the fuzzification of the variables associated with the constraints.The concept of Fuzzy logic was applied to all penalties, with penalty degrees ranging from 0 to 1. These degrees were subsequently multiplied by their respective penalty coefficients, allowing for a more gradual and realistic penalization. Trapezoidal membership functions were adopted to define the penalty degrees of all variables related to the constraints.The choice of this format is justified by its proven suitability in previous studies, such as [29,30], in which the trapezoidal function proved effective for variables such as reservoir levels, pressures at consumption nodes, and the number of pump and valve activations. Figure 3 illustrates the application of the Fuzzy concept to Penalty 1.
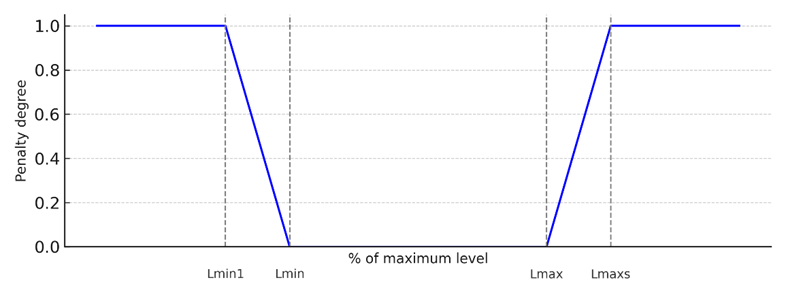 | Figure 3. Application of the Fuzzy concept to Penalty 1 |
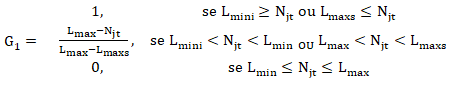 | (6) |
2.4. Hydraulic Model
- The hydraulic simulator used for the optimization of the Descoberto Water Supply System (WSS) was EPANET 2.0. The conceptual hydraulic scheme used in the study was based on the dynamic model proposed by [22], with some simplifications. In the literature, several studies on water supply system optimization use a reference system called Anytown, which has a reduced number of operational units, as in the works of [27,31,32]. On the other hand, studies such as [33,34] simulate real and more complex systems.The scheme of the Descoberto System used in this study includes a total of 273 nodes, consisting of: 23 reservoirs with variable levels, 1 fixed-level reservoir, and 35 consumption nodes. It also comprises 331 hydraulic links, of which 267 are pipelines, 47 are pumps, and 17 are valves. This set represents a high number of operational units, giving the model greater complexity compared to systems commonly adopted in the literature, which is a significant differentiating factor of this study. The hydraulic model of the Descoberto WSS is illustrated in Figure 1.The original hydraulic model had a high number of nodes and links, which significantly increased the processing time during optimization. Therefore, a simplification or skeletonization process was adopted, as applied in previous studies such as [18,35,36], to reduce computational time without compromising the hydraulic representativeness of the system. This simplification was performed through the creation of equivalent links by combining series and parallel links. For this purpose, the equivalent length equations presented by [37] were used. It is important to emphasize that no operational unit, nor any consumption node, was simplified during the process, ensuring that critical elements for system operation and control were preserved.The EPANET 2.0 model used monthly average consumption values, which implies that the operational rules adopted represent an average system operating condition. The model calibration was performed through a 24-hour extended simulation, using a known operational rule previously applied in the real system. The calibration process was conducted iteratively, with adjustments to head loss parameters, pump curves, and consumption patterns until the simulated reservoir levels approximated the observed field values. Model validation was not performed, as this structure was previously adopted by the company and considered already validated for operational purposes.
2.5. Optimization Algorithms
- Different algorithms were tested to optimize the operational electricity costs of pumping in the Descoberto Water Supply System (WSS). The algorithms evaluated were the Genetic Algorithm (GA), Dynamically Dimensioned Search (DDS), and Differential Evolution (DE). The GA, originally proposed by Holland [38], was selected for the main simulation, as it and its extensions, such as NSGA-II (Non-dominated Sorting Genetic Algorithm), are widely used in the literature for WSS optimization problems [6,15,27,39,40].Among evolutionary algorithms, the Genetic Algorithm (GA) was one of the first to be applied to the optimization of water supply systems (WSS). GAs are computational search and optimization methods for complex problems, inspired by the mechanisms of natural selection and survival of the fittest, as described in Charles Darwin’s Theory of Evolution (1859).The basic operational cycle of the simple genetic algorithm (Figure 4) begins with the creation of the initial population, which consists of a set of solution vectors representing the initial values of the decision variables. This population can be generated randomly or defined by the user. The fitness function is then evaluated for each vector. Subsequently, it is verified whether the stopping criterion has been met; in this case, the criterion is the number of GA generations. If the criterion is satisfied, the algorithm terminates; otherwise, the processes of selection, crossover (recombination), and mutation are applied to generate a new population for the next evaluation of the fitness function. This cycle continues until the stopping criterion is met.
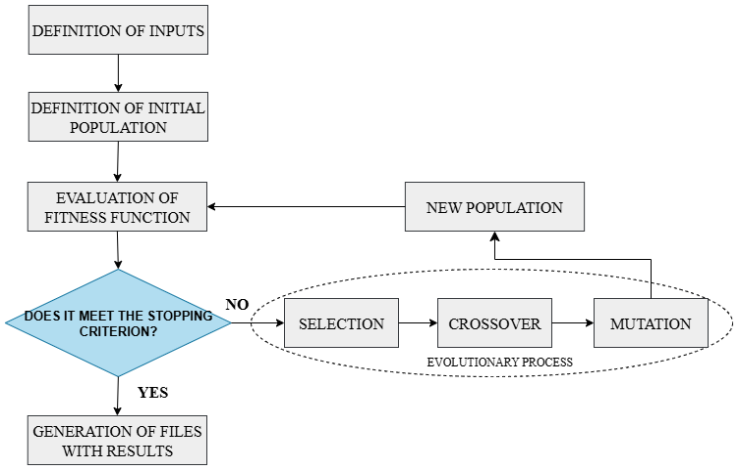 | Figure 4. Basic Operation of the Genetic Algorithm (GA) |
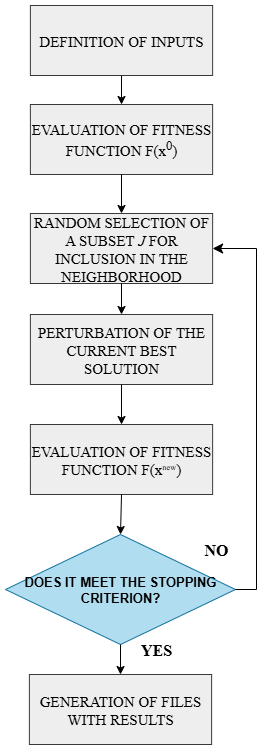 | Figure 5. Basic Operation of the DDS |
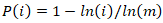 | (7) |
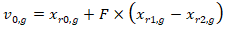 | (8) |
2.6. Input and Output Data of the Optimization Model
- The input data considered for the simulation of the optimization model were as follows:• Algorithm parameters: For the GA, the genetic operators previously calibrated by Gebrim [22] were used, as described in the previous section. For the DDS, a sensitivity analysis of the parameter was performed, setting the value of r = 0.3. For the DE algorithm, different combinations of the parameters F and CR were tested through sensitivity analysis, with the best results obtained for F = 0.6 and CR = 0.8.• Penalty coefficients: Defined based on the values used by Gebrim [22], considering the sensitivity analysis already conducted and the similarity to the problem under study, with the values presented in the previous section.• Initial solution (rule): Based on an actual operational rule used by the company responsible for the Rio Descoberto water supply system, aimed at accelerating the model processing. The initial fitness of this rule corresponds to 1,980,000. The rule consists of a set of 768 binary variables (0 or 1), where 0 represents the off/closed state and 1 the on/open state.• Number of objective function evaluations: A population size of 10 was considered — a value that produced the best results in Gebrim's simulations [22] — and 1,000 generations, totaling 10,000 objective function evaluations.• Maximum and minimum limits for applying the degrees of penalization in the fuzzy approach, according to the values previously presented.• Data for calculating electricity costs, as shown in Table 2.In total, the system under study consists of 5 energy-consuming units, where 10 pumping stations are installed, totaling 22 pumps involved in the optimization problem. The calculation was performed considering the location of each pumping station and its respective consumer unit, according to Equation 1, which presents the objective function.Additionally, input data were required in the EPANET 2.0 software, including:• Hourly consumption data over 24 hours, defined based on monitoring records from the water supply company and data from Gebrim [22], considering it is the same water supply system.• Start of operation: set at 06:00, as Gebrim [22] verified that at this time the reservoirs reached their maximum level, and it corresponds to the actual start of operation, which approximately coincides with the arrival of the operators at the company.• Initial reservoir levels: set at 98% of the maximum level, aimed at providing better hydraulic benefits and, consequently, greater operational safety.Based on the input data and the simulations performed, the model was able to generate the following output data:• Energy consumed in pumping operations.• Electricity costs.• Node pressures.• Reservoir levels.• Water flows in the network segments.• Algorithm processing time.• EPANET processing time.• Total processing time.• Objective function value and fitness function value.• Penalty values.• Operating status of pumps (on/off) and valves (open/closed), with on/open represented by 1 and off/closed represented by 0, as shown in Figure 6. This set is also referred to as the operational rule.
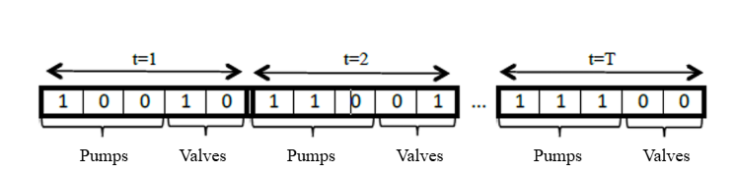 | Figure 6. Example of the operational rule representation for three pumps, two valves, and optimization period T. Source: [22] |
3. Results and Discussion
- The optimization model of the Water Supply System (WSS) was developed to minimize the total electricity cost for the operation of the Descoberto System over a 24-hour period. The model formulation considered the calculation of the energy consumption of each pump, the demand-related cost, and penalties associated with operational variables such as pressures at consumption nodes, reservoir levels, and the number of pump and valve activations. For each solution generated by the algorithm, which is represented by an operational rule, the model performs a hydraulic simulation using the EPANET software. This provides the values of the hydraulic variables, which are then used by the algorithm to calculate costs and penalties. Based on these results, the fitness function is evaluated, and a new rule is generated, repeating the process until all predefined function evaluations are executed.The model operation is based on penalizing rules that are operationally unfeasible. This includes activations that would result in pressures outside the limits established by technical standards, reservoir levels that are too high or too low, excessive pump starts, as well as variations between minimum and maximum levels exceeding a predetermined limit. Thus, the model ensures that optimized solutions respect the operational constraints of the real system.Simulations showed that, although the model was capable of finding solutions with reduced operational costs, many of these solutions would not be practically feasible. This occurs because some operational rules generated, while economically efficient, did not meet safety and operational reliability criteria. Such rules were automatically discarded by the optimization process. At the end of the simulations, the model was able to identify the operational rule closest to the ideal, reconciling practical feasibility with the lowest possible energy cost within the established operational limits. These results demonstrate the potential of the model as a decision support tool for the efficient operation of water supply systems.
3.1. Optimization Model
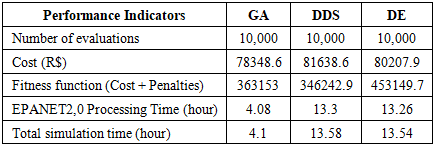
- To obtain the operational rules through the optimization algorithms, a fixed number of 10,000 fitness function evaluations was defined, with all algorithms starting the simulation from the same initial solution.The results obtained from the simulations carried out using the GA, DDS, and DE optimization algorithms, considering the same number of objective function evaluations (10,000), are presented in Table 3.
|
3.2. Operational Rules
- The optimized rule was obtained from the application of the Genetic Algorithm (GA), associated with Fuzzy penalization, using the simplified hydraulic model and the seeding technique for initialization. This combination allowed accelerating the model’s convergence and ensuring greater operational feasibility of the solutions. The final rule found did not result in pressures below 10 m.c.a. nor in reservoir levels outside the predefined limits, thus ensuring the continuity of supply over the 24-hour simulation and the applicability of the solution to the real system. However, a total of 26 activations above the recommended limit was observed, which is considered high for the practical operation of Water Supply Systems (WSSs).The pumping cost for the reference rule practiced by the company at the time of the simulation was R$ 85,934.50, while the cost associated with the optimized rule was R$ 81,327.50 — representing a savings of 5.3%. Although significant, this reduction could have been even higher if not for the already high efficiency present in the Descoberto System. It is noteworthy that the company has a technical team dedicated to managing energy consumption and that the Descoberto system alone operates near its structural limit.The total operating cost of the WSS comprises the demand cost of the consumer units and the consumption cost of the pumps, which depends directly on the operating time and the energy tariff, varying between peak and off-peak periods. The savings observed in the optimized rule are related to the strategy adopted by the model, which prioritized a smaller number of pumps in operation, both during peak and off-peak periods. Consequently, the number of activations increased, aiming to maintain other criteria within the stipulated penalty limits.The highest-power pumps, located at the Raw Water Pumping Station (5,500 and 11,000 hp), were responsible for a significant portion of the costs: 0.79% in the optimized rule, 0.83% in the reference rule, and 0.81% in the rule presented by Gebrim [22]. These values confirm that high-power pumps have a great impact on energy costs and, therefore, must be operated with special attention to minimize pumping costs, given their critical role in conveying water throughout the system. In contrast, lower-power pumps (100 and 150 hp) had an insignificant impact on the total cost, even when operating for prolonged periods: 0.011% (optimized rule), 0.006% (reference), and 0.009% [22]. This demonstrates that their continuous operation does not represent a significant increase in costs, allowing greater operational flexibility without impairing economic efficiency.Figures 7 and 8 illustrate the comparison among three operational strategies: the optimized rule proposed in this study, the reference rule adopted by the company at the time of the simulation, and the rule obtained by Gebrim [22]. Figure 7 shows the four pumps of the raw water pumping station, with powers between 5,500 and 11,000 hp, while Figure 8 displays smaller pumps (100 to 150 hp). Pumps in operation are represented in blue. In the reference rule, there is a tendency for continuous operation or few maneuvers, as in the case of pumps B2_AB, B1_AB, and B4_AB (Figure 7). This strategy aims to reduce mechanical wear of the equipment, prioritizing a lower number of activations. In all analyzed rules, there is a clear tendency to avoid peak hours (6 p.m. to 8 p.m.), which have the highest energy tariffs, as a way to reduce operational costs. Although the optimized rule resulted in a higher number of activations, all high-power pumps remained within acceptable operating limits.Figure 7 shows a greater tendency to avoid pump activation during peak hours in the reference rule. In the optimized solution, whose objective is the minimization of operational costs (objective function), the same strategy is also adopted.
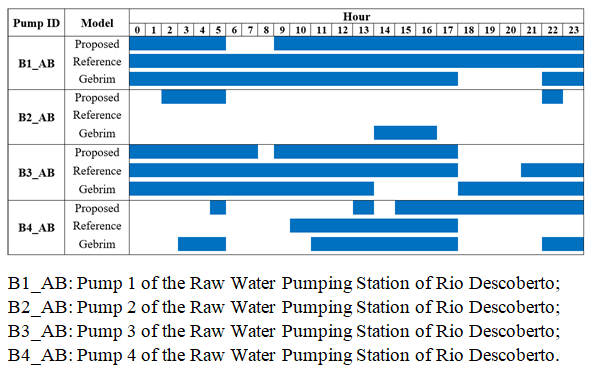 | Figure 7. Operational rules for pumps with power equal to 5,500 and 11,000 hp |
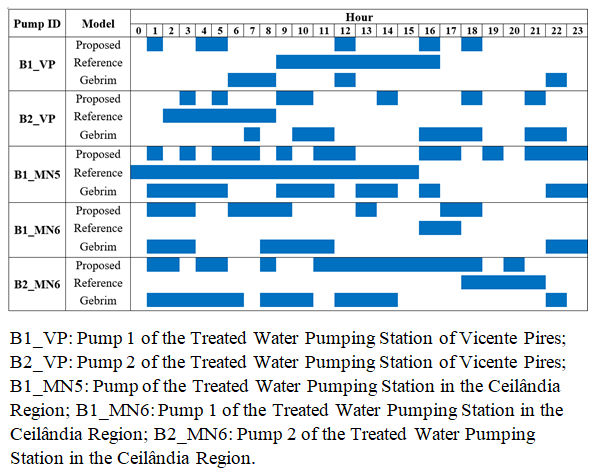 | Figure 8. Operational rules for pumps with power equal to 100 and 150 hp |
3.3. Reservoir Water Levels
- The reference rule resulted, at the end of the simulated period, in water levels lower than those at the start of the simulation in some cases, as observed in the Riacho Fundo reservoir (Figure 9). According to Gebrim [22], this behavior may indicate that, in real operations, system control is not based solely on the condition that the final reservoir level must be greater than or equal to the initial level. Instead, it is assumed that the initial level is sufficient to support the daily consumption cycle. This principle is also observed in the rule proposed by Gebrim [22], in which reservoir operation starts at 30% of the maximum level and ends at 79%. This demonstrates that the operation aims to ensure that daily demand is met safely, even if the levels do not return exactly to the initial condition by the end of the day.These results point to the need to consider more flexible operational strategies in optimization models, better reflecting real system practices, especially in contexts where the initial and final reservoir volumes do not need to match, as long as daily supply is ensured.At the end of the simulated period, the reference rule resultedin water levels lower than those at the start of the simulation in some cases, as observed in the Riacho Fundo reservoir (Figure 9). According to Gebrim [22], this behavior may indicate that, in real operation, system control is not based solely on the condition that the final reservoir level must be greater than or equal to the initial level. Instead, it is considered that the initial level is sufficient to support the daily consumption cycle. This principle is also observed in the rule proposed by Gebrim [22], in which the reservoir operation starts at 30% of the maximum level and ends at 79%. This demonstrates that the operation aims to ensure daily demand is met safely, even if levels do not return exactly to the initial condition by the end of the day.
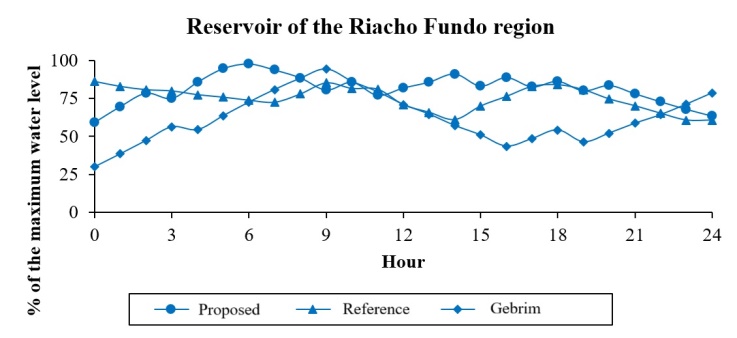 | Figure 9. Water Levels in the Riacho Fundo Reservoir |
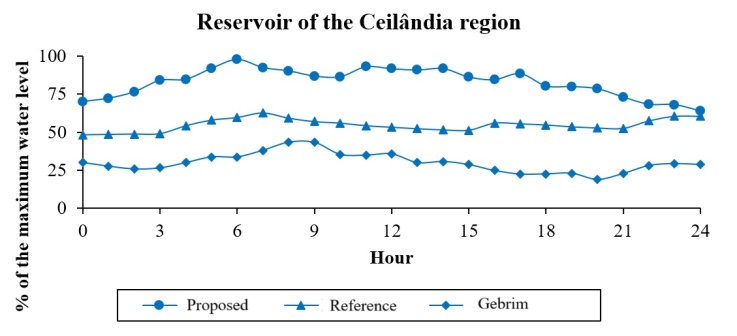 | Figure 10. Water Levels in the Ceilândia Reservoir |
4. Conclusions
- This study developed an optimization model for the pumping operation of the Rio Descoberto Water Supply System, located in the Federal District, using Genetic Algorithms (GA) in conjunction with the EPANET 2.0 hydraulic simulator and Fuzzy Logic. The results demonstrated that system optimization allows for a reduction in electricity costs while respecting established operational constraints. Moreover, the model proved capable of rapidly establishing operational rules close to the optimum, which is promising in scenarios involving system modifications, including the potential integration of the Corumbá IV Water Production System into the Rio Descoberto System—a possibility to be explored in future studies.The application of the optimized operational rule resulted in a 5.3% reduction in energy costs compared to the simulation of the reference rule. Additionally, higher reservoir levels were achieved, contributing to increased operational safety, further reinforcing the model’s potential for practical application. However, the high number of pump and valve activations observed in the simulations represents a significant limitation, as such behavior is undesirable in real operations due to the risk of equipment wear.Although the proposed model does not use a multi-objective approach, the results indicate that its application in real operations is feasible, particularly as it produces solutions close to the operational conditions currently adopted. This is reflected in aspects such as the maintenance of reservoir levels, adequate supply pressures, and relatively low processing time (1.09 hours), considering the system’s complexity and the number of evaluations performed.For real-time implementation, however, additional techniques would need to be incorporated, such as mechanisms to reduce the number of activations and the development of a demand forecaster—here considered as previously known, but in practical operations, subject to variations. Furthermore, complementary studies are recommended, including hydraulic reliability analyses of the system and the formulation of specific rules for operational emergency situations, to enhance the robustness and applicability of the proposed model.
ACKNOWLEDGEMENTS
- The authors acknowledge the Coordination for the Improvement of Higher Education Personnel (CAPES) for granting the scholarship to the first author and the Environmental Sanitation Company of the Federal District (CAESB) for providing the data used in this research.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML