Happiness Mac-Eteli1, Mobolaji Omobowale2, Goodnews Arube1
1Department of Civil Engineering, Niger Delta University, Bayelsa State, Nigeria
2Department of Agricultural and Environmental Engineering, University of Ibadan, Ibadan, Oyo State, Nigeria
Correspondence to: Happiness Mac-Eteli, Department of Civil Engineering, Niger Delta University, Bayelsa State, Nigeria.
| Email: |  |
Copyright © 2022 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
Hydraulic structures are designed for conveyance, structural integrity and sustainability. Flood prevention and control is more than ever creating a significant gap for the research society. Particularly for the southern and deltaic regions of the globe. The ease of design embodies the beauty of design. With the ever-rising climatic effects on the earth primarily due to human activities, and prevalent rise in global sea and river levels, the design of channels to manage water bodies in cities and towns is of primary importance. This paper uses basic hydraulic principles to develop analytical equations which were programmed in Microsoft Excel to design for all sectional properties of open channels as well as plot the cross section of the channel using four key variables of peak flow, channel bed slope, channel side slope, and roughness coefficient. The developed model is an enhanced calculator in the hydraulic engineering society due to its ability to function satisfactorily without prior knowledge of base with or flow depth.
Keywords:
Open Channel Flow, Calculator, Freeboard, Continuity equation, Flow depth
Cite this paper: Happiness Mac-Eteli, Mobolaji Omobowale, Goodnews Arube, A Technical Report on the Development of an Analytical Calculator for the Design of Hydraulic Sections for Open Channel Flows, International Journal of Hydraulic Engineering, Vol. 11 No. 1, 2022, pp. 10-15. doi: 10.5923/j.ijhe.20221101.02.
1. Introduction
Growing deserts, as well as a rise in the magnitude of floods and droughts, are some of the most visible climate change impacts [1]. Flood management embodies structural and non-structural approaches. Structural flood management schemes involve the design, construction and maintenance of drain systems, damns, dykes, and hydrodynamic structures, [2]. If the speed of inflow is same as that of outflow, flooding will not be experienced. However, the capacity of drain systems to effectively carry and discharge a body of flowing water is a function of the bed condition as well as the channel geometry. Nuttle et al (1992) [3], researched on the argument that increasing sea levels will boost surface runoff while lowering groundwater flow in a coastal watershed. This cannot be said to be applicable to cities and towns surrounded by rivers. A rise in river levels due to excessive rainfall or damn openings will limit its ability to receive inflow from its environment, hence an accumulation of excess water in soils and drains becomes the prevailing reality. For this reason, drains are designed to manage peak floods at estimated return periods with an allowance for safety carefully called freeboard. Excess runoff and ground water from paved streets, parking lots, sidewalks, and rooftops are drained via a storm drain system [4]. The Natural Resource Conservation Service under the United States department of Agriculture [5] has developed several spreadsheets for the calculation and design of hydraulic sections for piped and open channels. Fang [11] also developed a complex open channel flow calculator (Fig. 1), for trapezoidal, rectangular, triangular as well as circular channels. Whilst the calculator has a vast coverage, like most available calculators, it requires prior knowledge of bottom width and flow depth to activate its application [6,7,11,12]. The calculator developed by Richard [12] focuses only on the geometry of the channel as a function of width and depth for rectangular channels, side slope and depth for triangular channels and side slope, width and depth for trapezoidal channels. The dependent kinetic variables of discharge and velocity of flow were not integrated as components of the calculator. Adding to these existing developments, this paper will attempt to develop a tool for open channel flow calculations and design with no prior knowledge on base width or flow depth. 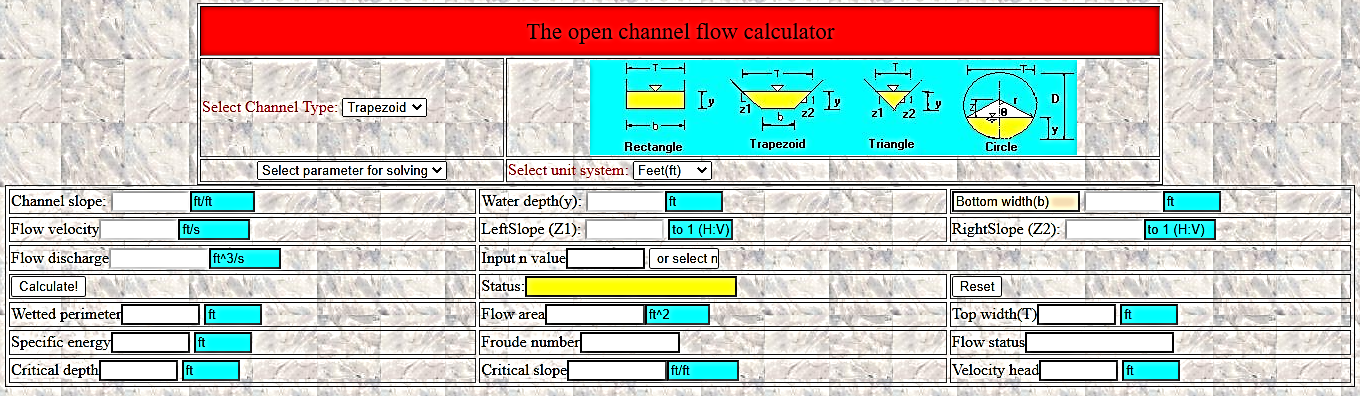 | Figure 1. The Open Channel Flow Calculator [11] |
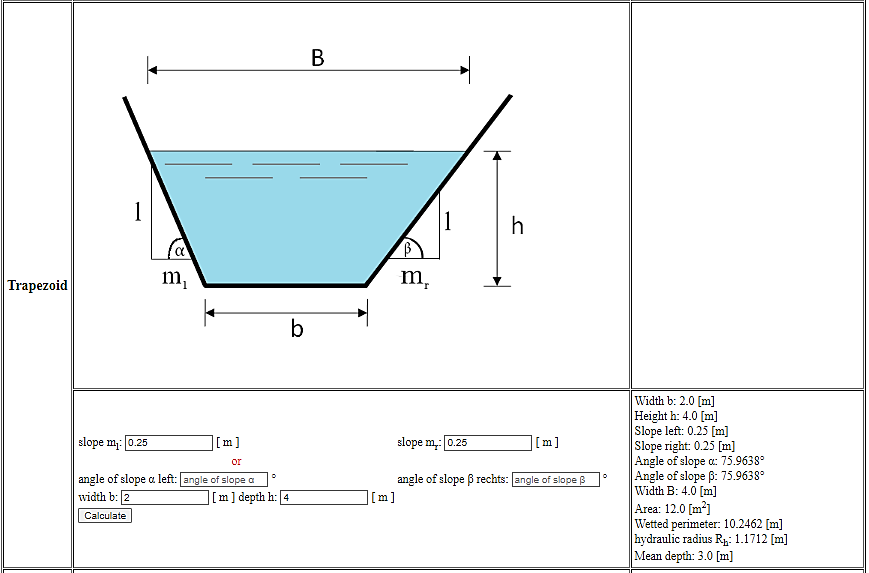 | Figure 2. Online Calculation of Open Channel Flow [12] |
The effect of erosion on river banks particularly in alluvial soils is of great concern to the engineering profession. According to National Engineering Handbook (NEH) [10], erodible channels in alluvium are designed for permissible flow velocity primarily by adjusting the slope, width, depth and planform of the flow channels. Additionally, a flow velocity of 0.61m/s is recommended for sandy silt earthen soils [10], for a regime channel condition to be maintained. In essence, an equation which embodies the above variables can simply be used to predict the optimum dependent variables in order to reach the desired flow velocity. As such, open channel flow calculators are tools for solving real life as well as dynamic problems. In implication, calculators in this field of study should have the capacity to adapt to these dynamics of changing slopes and cross-sectional areas as well as yield all related geometric as well as kinetic dependent variables. Adding to these existing developments, this paper will attempt to develop a tool for open channel flow calculations and design, with the ability to function effectively in the absence of base-width or flow-depth, having a scaled two-dimensional (2D) cross-sectional simulation template.
2. Methodology
This is an analytically based paper that incorporates basic hydraulic principles in the development of programmed analytical tool for the explicit and time saving design of the sectional properties of open channels. Using the equation of continuity and Chezy, an equation for the depth of flow, defined in terms of flow rate, bed slope, channel side slopes, and Manning’s constant was developed, and made the centroid of all other outputs or responses. The basic assumption used for the analysis is that the derivatives of the channel’s perimeter of flow and the flow depth are equal, and their ratio equates to zero.
2.1. Deriving the Flow Depth (y)
Flow depth or depth of flow is the key ingredient behind the approach adopted in this report. This is because the area of flow and the hydraulic radius of flow all incorporates the flow depth.The following steps are used in arriving at the flow depth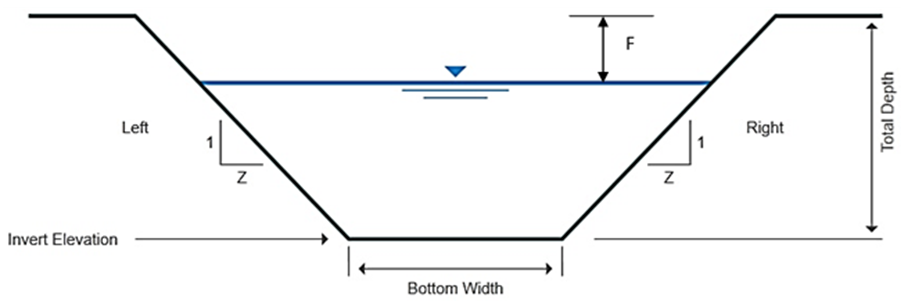 | Figure 3. Cross sectional area of a trapezoidal channel |
2.1.1. Continuity Equation
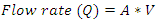 | (1) |
Where 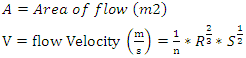 | (2) |
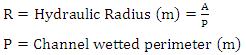 | (3) |
2.1.2. Channel Type
Trapezoidal channel is more conventional for open channel flows, as such, will form the basis for this report. In reality, natural channel side slope may differ, however, it is quite logical unless for some peculiar circumstances that the side slope of trapezoidal channel be designed to be uniform on both sides. This is taken as an assumption in this report. Hence, Z = Z1 = Z2 Where Z, Z1 and Z2 = side slope of a trapezoidal channel.Fig.3. Trapezoidal channel flow cross section.
2.1.3. Perimeter of Flow
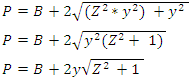 | (4) |
2.1.4. Define Channel Width (B) in Terms of Area, Depth and Side Slope
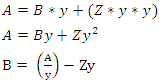 | (5) |
2.1.5. Define Area of Flow (A) in Terms of Flow Depth (y) and Side Slope (Z)
Substitute B in equation 5 into equation 4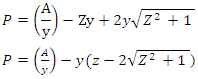 Differentiate P with respect to Y
Differentiate P with respect to Y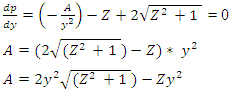 | (6) |
2.1.6. Define Flow Width (B) in Terms of Flow Depth (y) and Side Slope (z)
Substitute A in equation 6 back into equation 5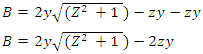 | (7) |
2.1.7. Define Flow Wetted Perimeter (P) in Terms of Flow Depth (y) and Side Slope (z)
Substitute equation 7 into equation 4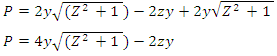 | (8) |
2.1.8. Define Hydraulic Radius (R) in Terms of Flow Depth (y)
From equation 3, 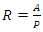 Substituting equations 6 and 8 into 3
Substituting equations 6 and 8 into 3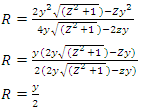 | (9) |
2.1.9. Define Flow Velocity (V) in Terms of Flow Depth (y), Manning’s Constant (n) and Bed Slope
From equation 2,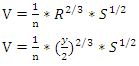 | (10) |
2.1.10. Define Flow Depth (y), in Terms of Flow Rate (Q), Manning’s Constant (n) and Bed Slope (S) and Side Slope (Z)
From equation 1,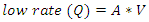 Substitute equations 6 and 10 into equation 1
Substitute equations 6 and 10 into equation 1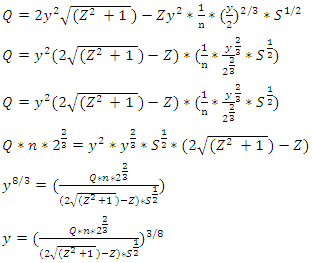 | (11) |
2.1.11. Freeboard (F) Defined as a Function of Flow Depth
There is much discrepancy on the ideal approach required for estimating the freeboard for open channels. While some suggest an ideal freeboard of 1/10th of the channel flow depth, others suggest the ideal factor to be 1/6th [6,7]. In this study however, considering the low topography of the southern region of Nigeria as well as the imminent annual flood challenges, a logical approach could be estimating the freeboard of a channel as 20% or 1/5th of the peak flow depth.i.e.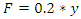 | (12) |
2.1.12. Channel Depth (D) as a Function of Flow Depth (y) and Freeboard (F)
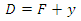 | (13) |
2.1.13. Top Width of Flow Section (T) as a Function of Side Slope (z), Channel Base Width (B) and Flow Depth (y)
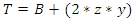 | (14) |
2.1.14. Top Width of Channel Section (M) as a Function of Side Slope (z), Channel Base Width (B) and Channel Depth (D)
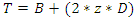 | (15) |
3. Results
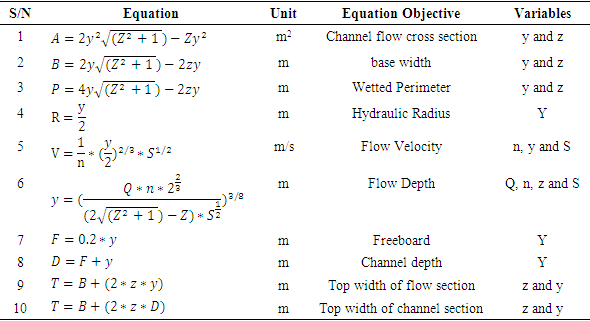
Table 1 below, is a summary of the derived equations required for the development of a statistical tool for estimating the geometric and flow properties of trapezoidal, rectangular as well as triangular open channels.Table 1. Standard Derivatives of a Trapezoidal Open Flow Channels
 |
| |
|
3.1. The Excel Template
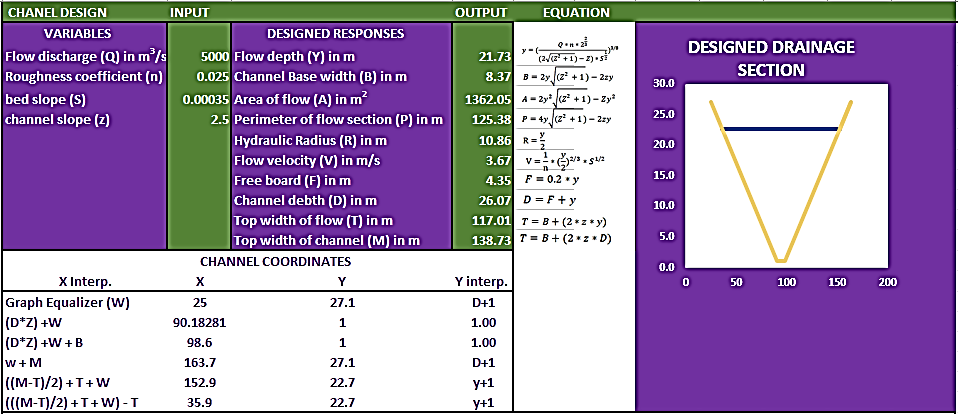 | Figure 4. Template for the design of open trapezoidal flow channel |
Fig. 4. is an excel template that functions as an open channel flow calculator, specifically for open channels with knowledge on flow rate (Q), manning’s constant (n), bed slope (S) and side slope (z). On inserting these four parameters as inputs, the calculator automatically develops the basic channel design properties as well as plots the cross section of the channel to scale. The calculator has been tested with existing calculators [8,9,11,12], and proves to be superior pertaining its ability to resolve flow channel problems with the least known parameters.
4. Conclusions
The paper has successfully explored the steps required in developing a custom-made open channel flow calculator for a trapezoidal channel with limited information. Using same principles, templates for sections such as triangular, semi-circular and rectangular channels can adequately be developed, all intended to ease the engineers stress and save time in the design and execution of open channels to curb ever growing flood challenges. This paper therefore introduces a new design tool to the engineering society enshrined with water and flood control and management.
ACKNOWLEDGEMENTS
We hereby acknowledge the profound technical support of Engr Banje Geofrey and the entire staff of the Department of Civil Engineering, of Niger Delta University, Bayelsa State, for providing a safe environment and atmosphere for research and deep study.
Conflict of Interest
We pledge that we are not involved in the interests of the financial, commercial, legal, or professional relationship with other organizations, or with the people we worked with them, that could influence this research.
References
| [1] | Misra, A. K. (2014). Climate change and challenges of water and food security. International Journal of Sustainable Built Environment, 3(1), 153-165. |
| [2] | Griffin, G., RAJABIFARD, A., & Williams, D. (2012). The Victorian emergency management continuum and the benefits of spatial enablement. |
| [3] | Nuttle, W. K., & Portnoy, J. W. (1992). Effect of rising sea level on runoff and groundwater discharge to coastal ecosystems. Estuarine, Coastal and Shelf Science, 34(2), 203-212. |
| [4] | Kumar, P. S., Santhi, T., Srivatsav, P. M., Reddy, S. S., Prasad, M. A., & Praveen, T. V. (2015). Storm water drainage design (Case study Vijayawada). Int. J. Earth Sci. Eng, 8(2), 507-511. |
| [5] | USDA, (2020). Natural Resource Conservation Service – Design Spreadsheet. United States Department of Agriculture (USDA), online source available on https://www.nrcs.usda.gov/wps/portal/nrcs/detail/md/technical/engineering/?cid=nrcseprd1337702. Last visited on 5/10/2021. |
| [6] | CivilWeb Spreadsheets, (2021). Engineering calculations and Spreadsheets -Manning Open channel Design. Online Source available on http://985.so/b1spu. Last Visited on 5/10/2021. |
| [7] | My Engineering World, (2011). Open Channel Flow Trapezoidal Section Calculator In Excel. Online source available on https://myengineeringworld.net/2011/05/open-channel-flow-trapezoidal.html. Last Visited on 5/10/2021. |
| [8] | Kenneth Alambra (2021). Omni Calculator - Open Channel Flow Calculator. Online Source available on https://www.omnicalculator.com/physics/open-channel-flow, last visited on 5/10/2021. |
| [9] | Civil Engineering, FAO, (2021). Freeboard and Open Channels. Online source available on https://www.openchannelflow.com/blog/free-board-and-open-channels, last visited on 05/10/2021. |
| [10] | National Engineering Handbook (NEH) (2007), Part 654 – Stream Restoration Design. Natural Resources Conservation Service, United Stated Department of Agriculture. |
| [11] | Zing Fang (2000). The Open Channel Flow Calculator. Department of Civil Engineering, Lamar University. Online Source available on https://www.eng.auburn.edu/~xzf0001/Handbook/Channels.html. |
| [12] | Berndt Wischnewski Richard 2022. Hydraulic Engineering - Channel Hydraulics - Online Calculation of Open Channel Flow. Online Source available on http://www.peacesoftware.de/einigewerte/gerinnehydraulik_e.html. |






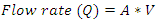
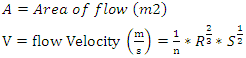
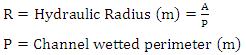
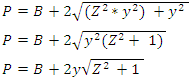
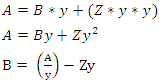
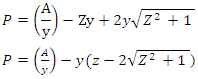 Differentiate P with respect to Y
Differentiate P with respect to Y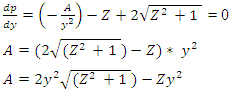
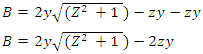
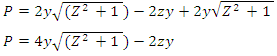
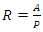 Substituting equations 6 and 8 into 3
Substituting equations 6 and 8 into 3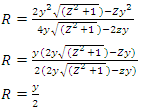
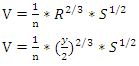
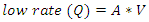 Substitute equations 6 and 10 into equation 1
Substitute equations 6 and 10 into equation 1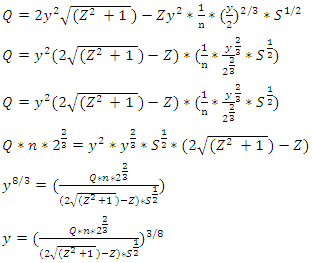
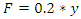
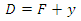
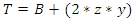
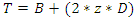


 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML