1. Introduction

It is now accepted that the presence of vegetation in aquatic environments serves various purposes, such as the improvement of water quality in wetlands and rivers (Wang et al. 2014; Rowiński et al. 2018, Afzalimehr et al. 2021), coastal protection against storm surges and waves (Möller et al. 2014; Luhar and Nepf 2016), providing a habitat for living organisms and aquatic species, and promoting biodiversity (Yi et al. 2017; Polvi and Sarneel 2018). Aquatic vegetation or macrophytes provide these valuable services through the alteration of flow field (Nepf 2012). Management of aquatic environments and the utilization of aquatic vegetation for the aforementioned services require modelling of the water-vegetation interaction and the underlying physical and biological processes (Marion et al. 2014).

The presence of macrophytes in aquatic environments decreases flow velocity and the conveyance capacity of open channels, as vegetation obstructs the flow and produces hydraulic resistance (Baptist et al. 2010; Green 2005b), consequently the water level rises which may cause flooding of adjacent lands which can be damaging especially in urban and agricultural areas (Rasmussen et al. 2021). Therefore, attempts are being made to find ways to reduce hydraulic resistance while maintaining the ecological functions of vegetated channels (Luhar and Nepf 2013).

Flow resistance due to vegetation depends on hydraulic and vegetation parameters, such as density, relative submergence, plant morphology, vegetation patchiness, and plant flexibility (Nikora et al. 2008; Fathi-Moghadam et al. 2011; Green 2006). Numerous sstudies have been done to evaluate the effect of different vegetation parameters on flow resistance (Green 2005a; Nikora et al. 2008; Järvelä 2005, Afzalimehr et al. 2019), but few have addressed the effect of vegetation patch distribution pattern on flow resistance. Literature shows that the effect of vegetation patch distribution on the flow field can have implications for flow resistance (Bal et al. 2011), contaminant removal efficiency (Sabokrouhiyeh et al. 2020), channel morphology, and sediment transport (Shan et al. 2020). Considering that vegetation occurs in heterogeneous patches in the natural environment (Anjum and Tanaka 2019; Schoelynck et al. 2012, Jahadi et al. 2020), this topic calls for a detailed investigation. Furthermore, vegetation is often removed from channels to facilitate flow of water and prevent flooding of adjacent lands (Bal et al. 2017; Errico et al. 2018).

This study experimentally investigates the effect of vegetation patch distribution on the flow field and flow resistance in a laboratory flume using five different distribution patterns of vegetation patches. The objectives of this study therefore are to obtain insights into the effect of patchiness on the hydrodynamics of vegetated channels and to determine the pattern of vegetation removal that causes the most reduction of hydraulic resistance.

2. Methodology

Experiments were conducted in a 13 m long and 0.45 m wide horizontal flume located at the Iran Water Research Institution. The water depth was fixed at 24 cm under submerged vegetation condition. 48 Wooden cylinders with a diameter of 1 cm and height of 10 cm were used as vegetation in the flume. Other studies have also used rigid cylinders to represent vegetation (Tinoco, San Juan, and Mullarney 2020). The cylinders were placed together to form different patterns of patches in each experiment (Fig. 1). The number of cylinders for the 5 experiments remained the same so as to keep the density of vegetation constant which was the main parameter effecting flow resistance (Nikora et al. 2008; Fathi-Moghadam et al. 2011). However, the distribution pattern was changed in order to compare the hydrodynamics of different distribution patterns. The patches were 10 cm apart in the transversal direction and 20 cm apart in the longitudinal direction (except for the last pattern in which the patches were 15 cm apart). The patches were placed at approximately 9 m from the flume entrance to reach the fully developed flow conditions. Gravel with uniform particle size distribution with d₅₀ =15 mm was used to cover the bed.

Figure 1. Distribution pattern 1 through 5 from the left

The velocity was measured using a propeller velocimeter which measured the velocity of water in the longitudinal direction of channel. In order to obtain the flow field, the velocity was measured in different cross-sections in the flume (5 cross-sections for the first 2 patterns and 6 for the rest of experiments) with 1 cross-section 10 cm before the leading edge of patches and 2 cross-sections 5 and 20 cm after the trailing edge. Five velocity profiles were measured within each cross-section at 7.5, 15, 22.5, 30 and 37.5 cm from the flume wall in the lateral direction with 8 points measured in the vertical axis in each profile at 3, 4, 5, 7, 10, 15, 20 cm from the bed and 1 point approximately at the water surface. In this study x, y and z are the longitudinal, lateral, and vertical directions, respectively. The flow velocity within the vegetated areas was not measured, since the velocimeter did not work well in this region.

Manning’s roughness coefficient was used to quantify the flow resistance (Salah Abd Elmoaty and T. A 2020; Li et al. 2014; Miyab et al. 2014, Afzalimehr Riazi 2020). After measuring the upstream and downstream velocity, Manning’s coefficient was calculated using equations 1 through 3, with V being the velocity, R the hydraulic radius, S the energy slope, l the length of the reach, H_f the friction loss, and h the water depth with u and d subscripts representing the upstream and downstream, respectively,

(1)

(2)

(3)

The Froude number for the 5 experiments was around 0.4 which has been observed in the field (Mohammadzade et al. 2015) and the Reynolds number was around 1.3×10⁴ showing the flow was subcritical and turbulent.

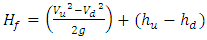3. Results and Discussion

After measuring velocity and flow depth at the upstream and downstream, Manning’s coefficient value for the 5 configurations was calculated (presented in table 1). Fig. 2 shows that Manning’s coefficient increased as the number of patches (N) increased (almost 40% for the last pattern) with the exception of the second and third configurations which had the same number of patches, however, the third configuration revealed approximately 11% more flow resistance than did the second one. Vegetation was clustered transversally in the second configuration, whereas it was clustered longitudinally in the third pattern.

Table 1. Hydraulic characteristics of experiments 1 through 5

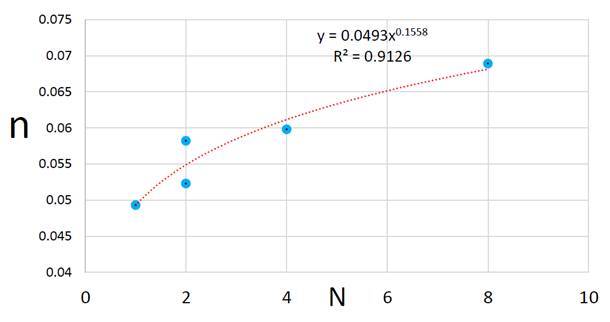Figure 2. Manning’s coefficient (n) against the number of patches (N)

This behavior was reported previously by (Luhar and Nepf 2013) who solved a set of equations developed by using a momentum balance to demonstrate that the flow resistance increased with the increasing number of distinct patches, even though the density of vegetation remained unchanged. Luhar and Nepf (2013) stated that by clustering vegetation into smaller distinct patches, the interfacial area between unobstructed water and vegetation patches increased which caused higher flow resistance. [Why?]

The third configuration led to 11% more resistance than did the second one, even though the second and third patterns both had 2 patches. However, in the second configuration, vegetation was clustered transversally, whereas in the third pattern vegetation was clustered longitudinally. Moreover, the fourth configuration had double the number of patches in comparison to the third, but producing only a little more than 2% resistance. Noting that the vegetation clustering from the third to the fourth configuration was carried out transversally. Taking these observations into account, it seemed that longitudinal clustering of vegetation caused more hydraulic resistance than did transversal clustering. Figure 3 presents Manning’s n against the number of patches in the longitudinal direction (N). Zhao and Huai (2016) studied the hydrodynamics of discontinuous vegetation patches similar to this study by experimental modelling and large eddy simulations, and stated that flow through vegetation was always non-uniform and the velocity and depth fluctuated as water flowed through vegetation. Discontinuous patches mean more fluctuations which cause more energy loss. However, in this study the velocity and the depth of water were stable without fluctuations when flow passed through patches.

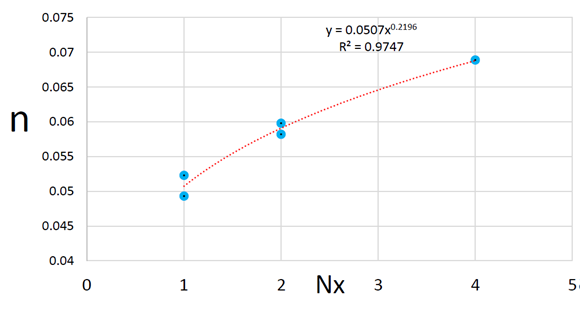Figure 3. Manning’s coefficient against the number of patches in the longitudinal direction

Bal et al. (2011) investigated the effect of 3 distribution patterns on the flow resistance and concluded that the flow resistance altered significantly when the distribution pattern of vegetation changed and generally the flow resistance increased by clustering patches into smaller patches. In their study, flow resistance increased only for higher discharges when the number of patches increased in the longitudinal direction.

Sabokrouhiyeh et al. (2020) evaluated the effect of vegetation distribution on the contaminant removal efficiency and concluded that longitudinally clustered vegetation led to more contaminant removal capacity because the flow residence was higher than in the case of elongated patches that were not clustered. Our results showed that longitudinally clustered vegetation produced more hydraulic resistance and that planners and designers must take this into account in addition to ecological and hydraulic considerations.

Figure 4 shows the velocity profile of the first, third and fifth sections of the third configuration at the center of the flume which was located 10 cm before the leading edge of patches, between the 2 patches and 5 cm after the trailing edge of the second patch, respectively. A secondary peak appears near the bed at y=4 cm in the first velocity profile. Comparing the first and third velocity profiles, it is clear that the presence of vegetation had completely altered the flow field, and velocity through the flow field decreased substantially whereas the velocity of the unobstructed field increased as the vegetation retarded the flow and the water was diverted to unobstructed regions of the flume. This alteration of velocity profile is typical of the submerged vegetation condition and has been observed in other studies (Yang, Huai, and Zeng 2020; Chembolu, Kakati, and Dutta 2019; Devi and Kumar 2016; Cui and Neary 2010). Comparing the third and fifth velocity profiles, it was observed that the velocity of the unobstructed region further increased and the depth decreased even more as the water passed through another patch of vegetation. A dip was apparent in the velocity profiles as velocity decreased near the water surface.

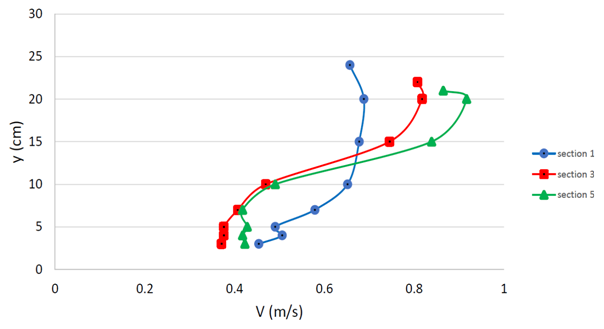Figure 4. Velocity profile of sections 1, 3 and 5 of the third configuration

Figure 5 shows the velocity contour of section 1 of the fourth configuration in the z-y plane, the contour is plotted from z=7.5 to z=37.5 cm because a fine grid of measurement needs in the y direction near the walls to achieve a reliable contour, due to considerable variation of velocity in that region. The velocity profile was taken 7.5 cm from both walls. In section 1 located 10 cm behind the patch, the velocity rose rapidly from the bed to approximately y=10 cm, showing the thickness of the boundary layer on the top of the gravel bed. In the outer region of this thickness, the velocity variation in the profile was not significant.

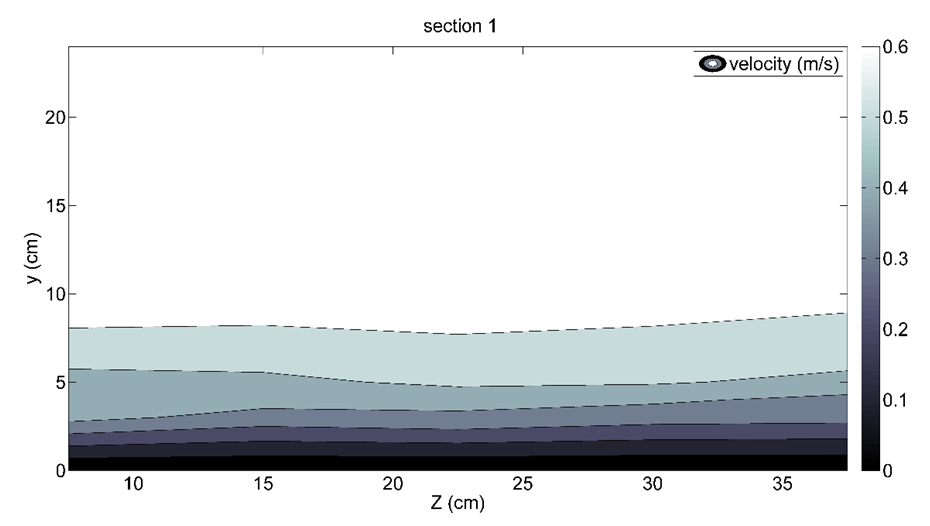Figure 5. Velocity contour of section 1 of the fourth configuration

In section 5 (Fig. 6) located 5 cm after the second row of vegetation, the effect of vegetation on the flow field was obvious, as the velocity reduced from z=9.5 cm to z= 17.5 cm behind the vegetation patch and then increased in the central gap between the patches from z=17.5 cm to z=27.5 cm and reduced again behind the second patch from z=27.5 cm to z=35.5 cm in the vertical direction. Accordingly, the velocity rose substantially in the upper regions, reaching 0.9 m/s. In the fourth configuration about 71% of the flow passed through unvegetated region in the flume as the flow was diverted to unobstructed regions. This part of flow was calculated by dividing the z-y plane into 5 areas and multiplying the mean velocity of each profile by the corresponding area.

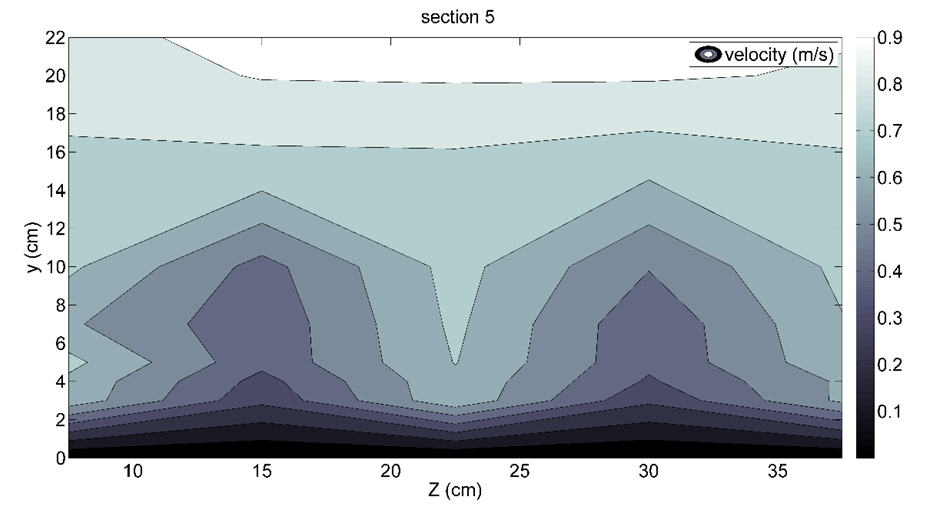Figure 6. Velocity contour of the section 5 of the fourth configuration

The section 1 of the third pattern was more or less the same as section 1 of the fourth configuration which was analyzed earlier, the mean velocity and the depth were the same and the velocity contours were nearly identical. However, in section 5 of the third configuration which is presented in figure 7, the flow field was different from that of the fourth configuration, the vegetated area which consisted of a single patch spanned from z=12.5 cm to z=25 cm in the transversal direction and from the bed to y=15 cm in the vertical direction which was discernible, as velocity had dropped significantly in this region. The velocity increased greatly in the upper unobstructed region and reached its maximum value near the surface in a short span as the water was diverted to the unvegetated regions where the depth decreased.

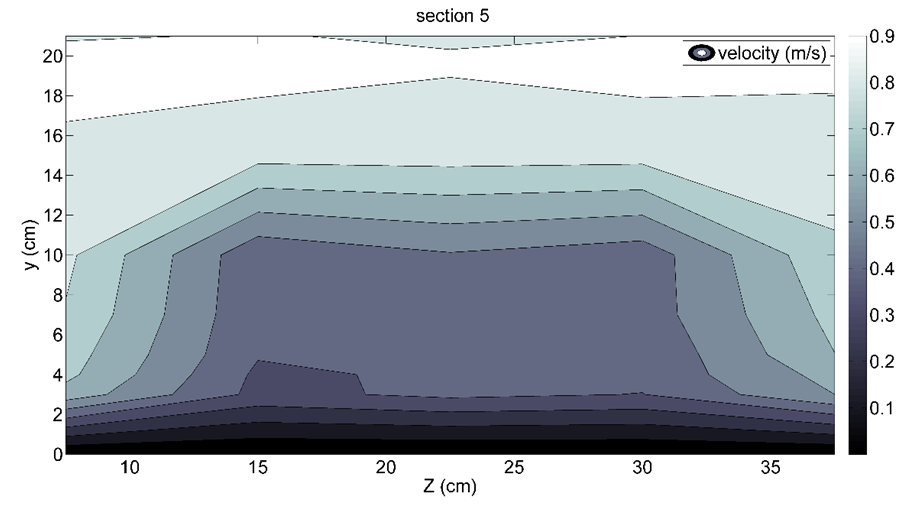Figure 7. Velocity contour of section 5 of the third configuration

Figure 8 displays the flow non-uniformity through vegetation for the velocity contour of the fifth pattern in the x-y plane. Noting that the velocity profiles were averaged in the z direction, and the flow in the upper unvegetated region rose as the flow passed through the patches in the x axis. However, the velocity changes were insignificant in the lower vegetated region, whereas some studies showed that the velocity and depth variations increased as the water passed through discontinuous patches of submerged vegetation (Ghani et al. 2019; Zhao and Huai 2016). This is because when the velocity increased, the flow depth decreased (25, 24.5, 24, 23, 22 and 21.5 cm in section 1 through 6) monotonically in the x direction.

Figure 8. Velocity contour of the fifth configuration in the x-y plane

It is known that water exerts a drag force on the vegetation patch, however, our results confirmed the previous study (Zhao and Huai 2016), that clustering of vegetation in the longitudinal direction produced extra flow resistance and consequently the drag force of water on vegetation patches increased. Natural vegetation is prone to breaking, dislodgement deflection, and generating more drag on vegetation, showing more hydrodynamic stress on the vegetation (Zhu et al. 2019) which is one of the reasons that vegetation usually grows longitudinally in continuous strips of patches in streams rather than in longitudinally clustered patches which has been observed in other studies (Yamasaki et al. 2019; Zhu et al. 2020).

4. Conclusions

Experiments were carried out to study the effect of vegetation patch distribution on the flow field and flow resistance using rigid cylinders representing vegetation. Results showed that flow resistance varied significantly with the changing vegetation distribution pattern, even though the density remained unchanged which is an important finding because the flow resistance models use density, submergence ratio, and flexibility as input parameters. To our knowledge, no flow resistance model has revealed the effect of different vegetation patch patterns. The longitudinal clustering of vegetation produces more hydraulic resistance than the transversal clustering which has been observed before. Results of this study provide a better restoration approach by considering optimal cutting and removal pattern of vegetation in open channel hydraulics.