Gwendoli Djaomazava 1, Michel Aimé Randriazanamparany 2, François D’Assise Rakotomanga 3
1Thematic Doctoral School – Renewable Energies, Antsiranana University, Hydraulic Laboratories, Madagascar
2Superior School Polytechnic, Antsiranana University, Hydraulic Laboratories, Madagascar
3Faculty of Sciences, Antsiranana University, Physical Laboratories, Madagascar
Correspondence to: Gwendoli Djaomazava , Thematic Doctoral School – Renewable Energies, Antsiranana University, Hydraulic Laboratories, Madagascar.
| Email: |  |
Copyright © 2019 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
A numerical study of the thermal natural convection applied in a vertical channel containing air, one of whose walls comprises a corrugated part subjected to a uniform heat flux of constant density, is the subject of this research. The work consists in characterizing the natural convection as a function of the height of the protuberances forming the undulations and the intensity of the heat flow, which crosses the corrugated wall. We analyze in particular the structure of the flow and the distribution of temperature inside the channel. Knowledge of different physical parameters on the behavior of the system can help to better understand its functioning and to integrate it effectively into practical applications such as, for example, passive climate control of building. The equations governing the transfers inside the channel are discretized by the explicit finite difference method, the results are illustrated using stream lines and isotherms, for a range of Rayleigh numbers from 5.103 to 5.105, for different values of the amplitude of the protuberances and for a number of Prandtl Pr = 0,71 for air.
Keywords:
Natural convection, Vertical channel, Sinusoidal protuberances, Finite difference method
Cite this paper: Gwendoli Djaomazava , Michel Aimé Randriazanamparany , François D’Assise Rakotomanga , Numerical Study of Natural Convection in a Vertical Channel, One of Whose Walls has Sinusoidal Protuberances, International Journal of Hydraulic Engineering, Vol. 8 No. 1, 2019, pp. 1-6. doi: 10.5923/j.ijhe.20190801.01.
1. Introduction
Transfers that develop by natural convection in a vertical channel where one of the walls is subjected to the uniform flow or maintained at a constant temperature different from that of the fluid have been the subject of numerous theoretical and experimental work because of their importance in areas as diverse as housing, drying, heat exchangers. Studies of natural thermal convection in a channel can be considered as irrefutable bases in the bibliographic referencing. Among the possible configurations, the heat transfers along a vertical channel with one of the walls present obstacles attracted special of attention. Many theoretical and experimental studies have been done in this area. CHENIER Eric [5] presented a numerical study of natural convection in a vertical channel whose sidewalls are heated symmetrically or asymmetrically at imposed temperature or imposed heat flux. The results that he has obtained show these natural convection flows are very sensitive to choice of open boundary conditions, particularly with regard to the structure and intensity of the flow. ZEGHMATI Belkacem [1] studied numerically the influence of a sinusoidal protuberance on natural convection transfers in a vertical channel. This protuberance is subjected to a uniform flow of constant density. He noticed that the influence of the protuberance on the transfers is all the more important as its amplitude and the density of the heat flux applied to it are high. For large values of the Rayleigh number, there appears a recirculation zone located at the outlet of the channel downstream of the protuberance. ZOUBIR Amine [11] carried out a numerical study on pure natural convection and convection/radiation coupling in an open channel partially heated in constant flux density. He found that if one considers the wall radiation, the structure of the flow changes completely: the return flow observed in the case of pure convection has disappeared and the flow has increased. In this paper, a numerical study of natural convection in a vertical wavy-wall channel is presented. We analyze the influence of the shape ratio of the corrugations and the heat flux density applied to the base of these undulations.
2. Modelization
The physical model studied is a vertical channel formed by two flat, parallel plates delimited by two vertical walls of height A and separated by a distance d. on one of the walls is fixed sinusoidal protuberances having the same height b. these protuberances are heated by injection to their base of a constant density heat flux q. The remaining parts are adiabatic. The contribution of heat by the conduction-convection protrusions to the air located in its vicinity generates a natural convection in the space delimited by the walls.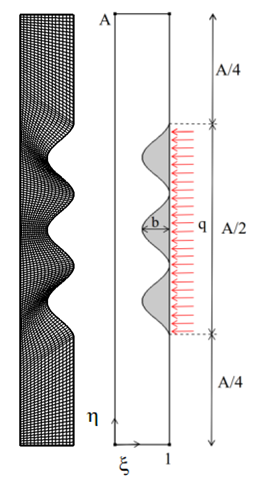 | Figure 1. Calculation domain and coordinate system |
The channel is thus traversed by a laminar rising flow of hot air. At the entrance, it has a temperature T0 (Fig. 1). Assuming that the Boussinesq hypothesis applies and the viscous dissipation is negligible, the equations governing the transfers in the space delimited by the two plates are the classical equation of natural convection. They are dimensioned by introducing the following dimensionless quantities: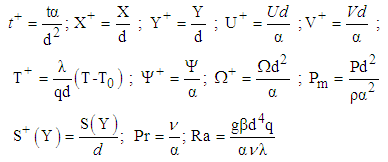 | (1) |
The dimensional coordinates (X, Y) define the physical domain. It will therefore be difficult to render the rectangular mesh according to these coordinates because nodes are located outside the domain because of the curvature of the sinusoidal wall. For that, it is transformed into a digital domain characterized by the parameters 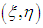 called homotopic coordinates to give it a virtual rectangular shape:
called homotopic coordinates to give it a virtual rectangular shape: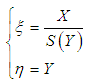 | (2) |
The relation below defines the dimensional profile of the sinusoidal protuberances: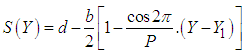 | (3) |
With these transformations, the transfer equations and the boundary conditions are rewritten in the homotopic coordinate system. The (+) exponent on dimensionless quantities is omitted to lighten the notations on the equations which, from now on, are all dimensional.Given the simplifying assumptions made and the transformation of the coordinates, the dimensionless equations are written as follows:• Heat equation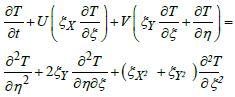 | (4) |
• Equation of vorticity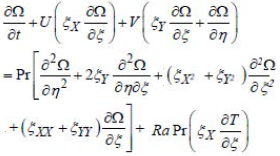 | (5) |
• Equation of the stream function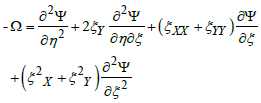 | (6) |
• Components of speed [3], [7], [13]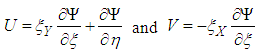 | (7) |
With, | (8) |
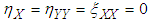 | (9) |
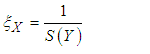 | (10) |
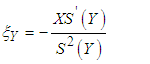 | (11) |
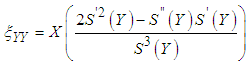 | (12) |
The initial and boundary conditions are:At t = 0, the fluid is at rest and the entire system is at the same temperature T0.Is: 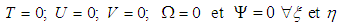 At the inlet of the channel:
At the inlet of the channel: 
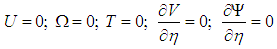 | (13) |
On the adiabatic left wall: 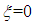
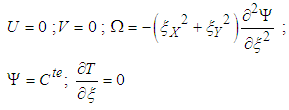 | (14) |
On the right heating wall: 
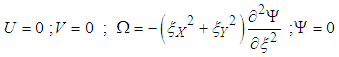 | (15) |
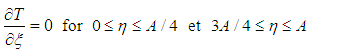 | (16) |
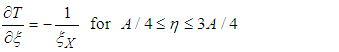 | (17) |
To the outlet of the channel: 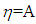
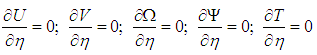 | (18) |
3. Numerical Resolution
Conservation equations describing flow and heat transfer are solved by approximating partial derivatives with explicit finite differences. The time derivatives are approximated by a finite difference of the first order between the instants t - ∆t and t (∆t being the time step). Equation (6) giving the stream function is solved by an iterative method. The relaxation coefficient is used to accelerate: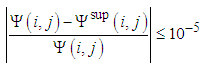 | (19) |
To ensure the accuracy of our results, the calculation code that we realized was validated on results of the literature. The comparisons made as part of this validation are reported below.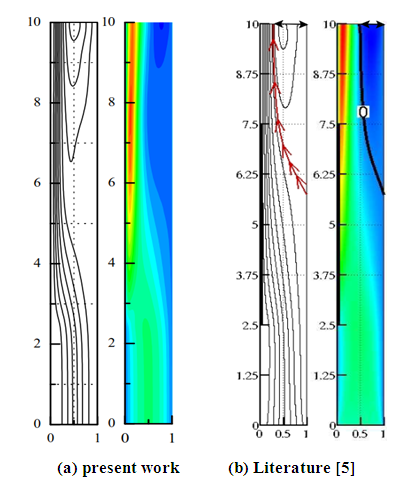 | Figure 2. Streamlines and velocity field for Ra = 5.105, Pr = 0,71 and A = 10. Comparison of results |
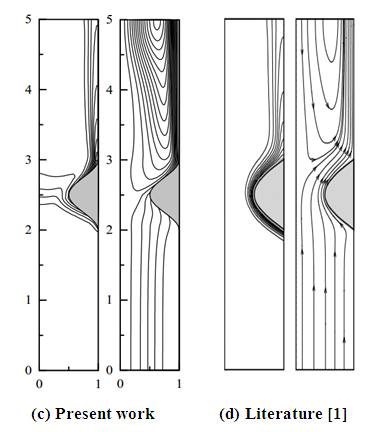 | Figure 3. Isotherms and streamlines for Ra = 5.105, Pr = 0,71 and A = 5. Comparison of results |
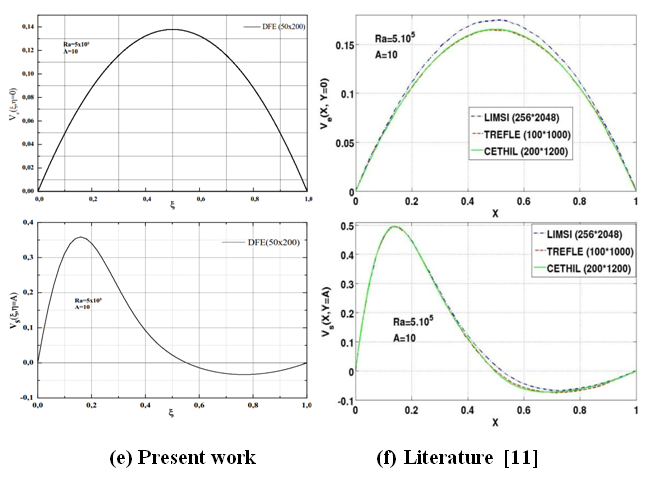 | Figure 4. Vertical velocities at the inlet and outlet of the canal for Ra = 5.105, Pr = 0,71 and A = 10. Comparison of results |
We tried to compare it with another closed system also our calculation code to better see its efficiency, on this confined space, one of the walls is heated. And we see a great similarity with the same study parameters.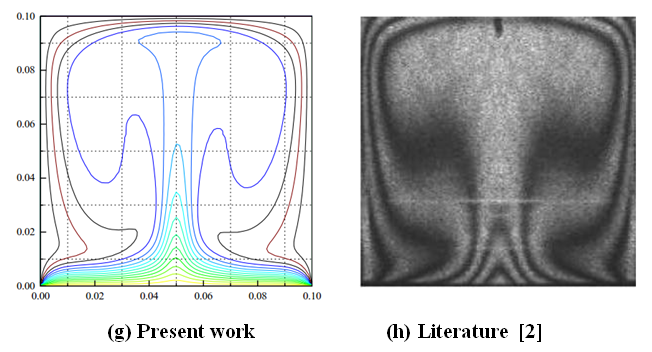 | Figure 5. Isotherms for Ra = 1,836.105, Pr = 0,71. Comparison of results |
4. Results and Discussion
The results are obtained from simulations carried out in the case where three protuberances are present in the channel, for different values of the height b of the obstacles, the number of Rayleigh Ra, fixing the length / width ratio of the channel at A = 8 and the Prandtl number at Pr = 0,71, the fluid being air. The stream and isothermal lines resulting from the calculations carried out are shown in figure 6 to figure 9.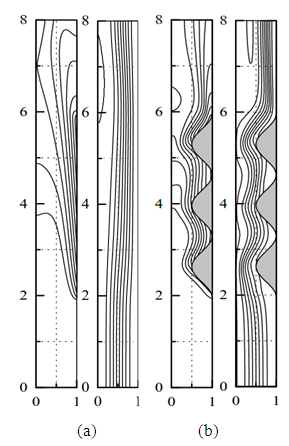 | Figure 6. Isotherms and streamlines for Ra = 5.103, Pr = 0,71, A = 8, b = 0 (a), b = 0,50 (b) |
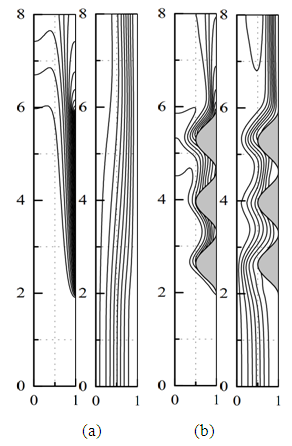 | Figure 7. Isotherms and streamlines for Ra = 5.104, Pr = 0,71, A = 8, b = 0 (a), b = 0,50 (b) |
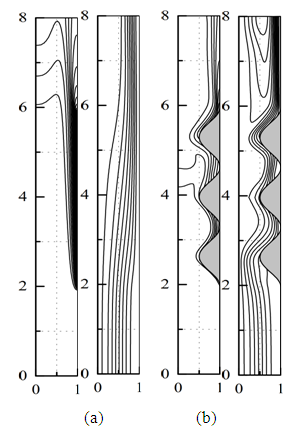 | Figure 8. Isotherms and streamlines for Ra = 2.105, Pr = 0,71, A = 8, b = 0 (a), b = 0,50 (b) |
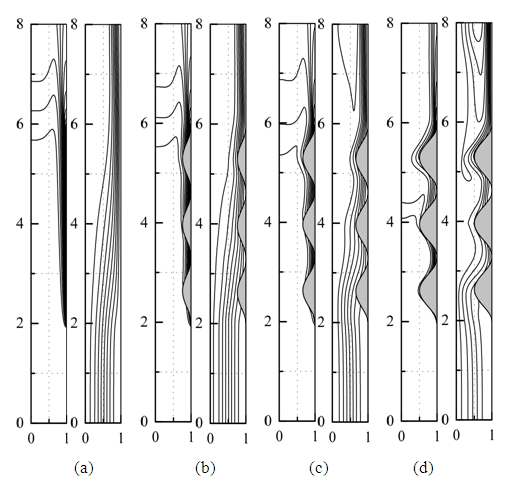 | Figure 9. Isotherms and streamlines for Ra = 5.105, Pr = 0,71, A = 8, b = 0 (a), b = 0,25 (b), b = 0,35 (c) et b = 0,50 (d) |
The results show that the structure of the flow is strongly influenced by the presence of the protuberances. Indeed, if we compare the streamlines without the protuberances (b = 0) and with the protuberances, we note the following differences. In the first case, the lines remain parallel to the walls over a large part of the channel before being deflected on the right wall where there is the heated part, in the vicinity of the outlet. This structure remains almost unchanged regardless of the Rayleigh number. In the second case, the settlement of the streamlines on the right-hand wall is more pronounced. In addition, the presence of the protuberances promotes the appearance of a recirculation zone in the vicinity of the outlet [4]. This recirculation intensifies, for given Rayleigh number, when increasing the height of the protuberances and, for given protuberance height, when increasing the Rayleigh number.From the thermal point of view, the air that enters the channel at room temperature heats up from the moment it comes into contact with the heated part of the wall. A non-uniform temperature distribution is established and causes the upward movement of the fluid. This movement intensifies with the increase in the number of Rayleigh that is to say when increasing the value of the heat flux injected on the heating wall. The isotherms indicate that the temperature distribution in the vicinity of the outlet is uniform when the protuberances are present.
5. Conclusions
This work that we carried out brought us on several horizons of the study of the natural convection. We modeled the system using the natural convection equations formulated in terms of vorticity and stream function. The non-rectangular geometrical shape of the channel with protuberances led us to proceed to a homotopic transformation of the equations. It is then a question of numerically solving the equation of the function of stream. The first two is solved with a direct calculation process while the stream function is iteratively calculated. The numerical results obtained allow us to make the following remarks:- The flow does not undergo any disturbance upstream of the protuberances; - For large values of the shape ration of the protuberances, there appears an air recirculation zone near the outlet downstream of the obstacles due to the abrupt change of the section of the channel and to the presence of the heat flow applied.- The modification of the amplitude of the protuberances implies an increase of the heat exchange surfaces inside this channel and, consequently, an intensification of the convection.As a perspective, we plan to do broader explorations using a wider range of influencing parameters. We also plan to carry out an experimental setup and make measurements to reinforce the validations.
Nomenclature
Latin letters Greek letters
Greek letters Exponent
Exponent
References
| [1] | B. Abdellah, R. Mebrouk et T. Abdelhamid, ‘‘Etude de l’influence d’une protubérance sinusoïdale sur les transferts par convection naturelle dans un canal vertical’’, 12ème Journnées Internationales de thermique, 2005. |
| [2] | B. Calcagni, F. Marsili, M. Paroncini, Natural convective heat transfer in square enclosure heated from below, Appl. Therm. Eng. 25(2005)2522-2531. |
| [3] | C. C. Wang, C. K. Chen, ‘‘Forced convection in a wavy wall channel,’’ Heat and Mass Transfer. 45, 2587-2795 (2002). |
| [4] | C.Garnier, ‘‘Modélisation numérique des écoulements ouverts de convection naturelle au sein d’un canal vertical asymétriquement chauffée’’, France, 2014. |
| [5] | E. Chénier, A. Joulin, ‘‘Convection naturelle d’air dans un canal vertical asymétriquement chauffé à flux imposé: exercice de comparaison et solutions de référence’’ Congrès Français de Thermique, Gérardmer, France. pp. Article 6144 (USB), 2013. |
| [6] | G. Desrayaud, A. Fichera, ‘‘Laminar natural convection in a vertical isothermal channel with symmetric surface-mounted rectangular ribs,’’ Int. J. Heat and Fluid Flow, Vol. 23, 519-529, 2002. |
| [7] | H. Nakamura, Y. Asoko and T. Naitou, ‘‘Heat transfer by free convection between two parallel plates,’’ Numer. Heat Transfer, Vol. 5, 39-58(1982). |
| [8] | R. J. Krane and S. A. M. Said, ‘‘An analytical and experimental investigation of natural convection heat transferin vertical channel with a single obstruction,’’ Int. Heath Mass Transfer, 33. |
| [9] | S. Prétot, B. Zeghmati, Ph. Caminat, ‘‘Influence of surface roughness on natural convection above a horizontal plate,’’ Advances in Engineering Software, Vol.31, 793 – 801, 2000. |
| [10] | W.M. Yan end T.F. Lin, ‘‘Natural convection heat transferin vertical open channel flows with discrete heating,’’ int. comm.heat mass transfer, vol. 14, pp.187-200,1987. |
| [11] | Z. Amine, S. Xin, S. Giroux-Julien, C. Ménézo, ‘‘Etudes numériques des transferts thermo-convectifs dans un canal d’air vertical à flux imposé’’, in: Proc. Of the annual congrès Français de Thermique, SFT Perpignan, 2011, 163-168. |
| [12] | I. Hashim, A.I. Alsabery, M.A. Sheremet, A.J. Chamkha, ‘‘Numerical investigation of natural convection of Al2O3 – water nanofluid in a wavy cavity conductive inner block using Buongiorno’s two-phase model’’, Advanced Powder Technology, Vol. 30, 399-414, 2019. |
| [13] | A.K. Hussein, S.H. Hussain, ‘‘Heatline visualization of natural convection heat transfer in an inclined wavy cavities filled with nanofluids and subjected to a discrete isoflux heating from its left sidewall’’, Alexandria Engineering Journal (2016) 55, 169-186. |



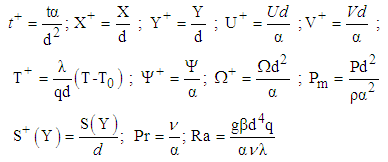
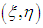 called homotopic coordinates to give it a virtual rectangular shape:
called homotopic coordinates to give it a virtual rectangular shape: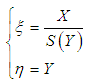
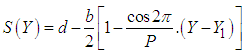
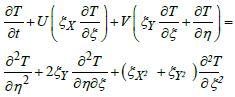
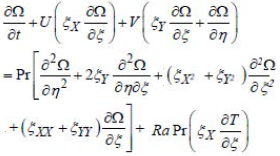
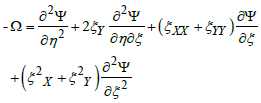
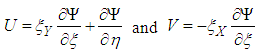

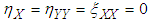
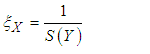
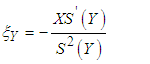
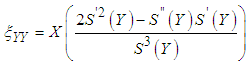
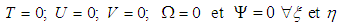 At the inlet of the channel:
At the inlet of the channel: 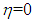
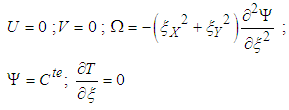
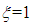
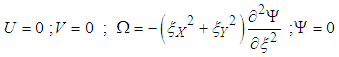
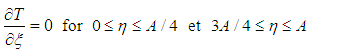
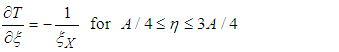
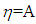
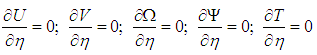








 Greek letters
Greek letters Exponent
Exponent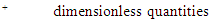
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML