1. Introduction

According to the United Nations (UN, 2014) 46% of the world’s population live in rural areas. While there is a consistent trend toward urban migration, the rural poor is still the demographic most likely to not have access to potable water.

Small gravity fed water systems relying on surface water sources are common in the developing world and high sediment loads can compromise their effectiveness. In monsoonal regions, especially in areas where deforestation has exacerbated the problem of watershed erosion, it is not uncommon for the peak flow, and thus the sediment load, during the rainy season to exceed the average annual flow by several times or even an order of magnitude. For example, the Mekong, a large river in Southeast Asia, has a typical peak annual flow at Luang Prabang, Laos, of around 12,000 cumecs (cubic meters per second) and a long term mean annual flow of approximately 3500 cumecs resulting in a peak to average flow ratio of 3.4 (Mekong River Commission, 2009). In 1978, the peak was about 77,000 cumecs giving a ratio of 22. This ratio is even more pronounced in smaller basins. In their study on the ratio of peak to average daily discharges, Ellis and Gray (1966) found that the instantaneous peak to average daily flow ratio decreased exponentially as the basin area increased.

Sediment in water systems reduces water quality and degrades the physical system. Water treatment plants and distribution systems are particularly susceptible (UNESCO 2011). These factors are especially challenging in developing world communities where basic infrastructure and financial resources are limited. The reality of sediment related problems in water systems is broadly acknowledged by water management professionals and efforts have been made to develop intake designs that reduce the sediment load. Raudkivi, (1993) proposes several alternative designs for small intake structures. He points out that countless structures have been constructed to provide water to communities all around the world and although these systems are small, the cumulative cost is significant.

This paper reports on the development and testing of a novel device to exclude sediment from small water systems using a Coanda effect screen. Consideration of realistic constraints commonly found in the developing world is a key objective.

The Coanda effect is named after Henri Coanda (1886-1972), a Romanian inventor and early aerodynamicist who observed that a fluid jet will tend to follow the contour of a solid surface (Circiu, not dated). Coanda effect screens (also called wedge wire screens) are used in the food processing industry and as fish and trash screens for hydropower intakes. Hosseini (2011) describes a project where Coanda effect screens were used to remove debris from a large flood control structure. A simple numerical model and a physical model were successfully employed to determine design parameters and flow detailing for design and setup of the screens.

No research has been found that attempts to study the utility of these screens for sediment exclusion from water supply intake systems.

2. Coanda Screen Structure

Screens (Fig.1) are typically installed in an overflow weir. The accelerator plate, space below the crest and above the screen, is used to assure an appropriate velocity over the screen (Fig. 2). Through-flow passes through the screen and is captured in a collection box where it is routed into a discharge pipe. Excluded sediment passes over the screen and is carried downstream by the bypass-flow. As a result the screen is self-cleaning.

Figure 1. Photographs of a typical Coanda effect screen in plan and longitudinal section views. This particular screen has a wire width of 3.2mm (1/8 inch), a wire tilt angle of 13° and a wire spacing of 0.3mm. The screen has dimensions of approximately 30cm x 20cm

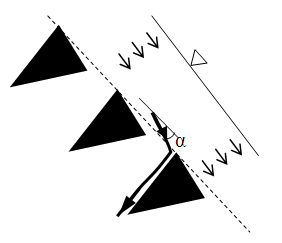Figure 2. A typical installation has the Coanda effect screen installed on the face of an overflow weir. Through-flow passes into a collection box and a discharge pipe routs the water downstream

The quantity of through-flow is controlled by two mechanisms. First is the flow driven by the effective hydrostatic pressure that results from the depth of water over the space between any two parallel wires. Wahl, (2001) developed an equation that describes the unit discharge through tilted wire screens. He shows that it can be put in the form of the typical orifice equation. The relationship is a function of two coefficients. One accounts for velocity reduction and contraction (C_cv) as the flow moves through the slot and the other (C_F) is dependent on the Froude number, the geometry of the wires and the angle of attack of the approaching flow. In Wahl’s model the depth of the flow above the slot is contained in the specific energy term that provides the driving force for the flow. The second flow mechanism is the thin layer of water that is sheared off the bottom of the flow section. As seen in Figs. 1 and 3, the individual wires are tilted resulting in an elevated leading edge on each wire. The sharp edge shears a portion of the water and directs it through the gap between the wires (Fig. 3). The Coanda effect is responsible for keeping the flow attached to the top face of the wire as it approaches the next wire. Screens are orientated so that the wires are perpendicular to the direction of flow and at a slope that assure supercritical flow on the face of the screen. Wahl (2001) reports Froude numbers across the screen between 2 and 30. The higher values occur near the toe of the screen in situations where there is little bypass-flow and thus the flow depth is small and velocity high, resulting in large Froude numbers.

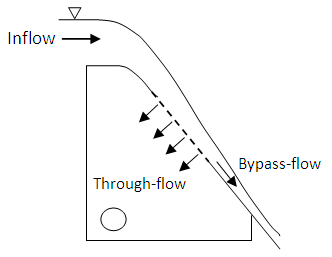Figure 3. A thin layer of water is sheared off by the leading edge of each wire. The angle of attack α is the critical parameter for determining through-flow

Wahl studied the flow characteristics of Coanda effect screens with a series of clean water, laboratory experiments. He originally developed a theoretical based computational model that used a modified orifice equation with the Froude number, Weber number and Reynolds number to predict the depth and velocity profiles across a screen (Wahl 2001). He found that screen curvature and air entrainment have a significant effect on flow performance but that the hydraulic friction derived from the flow over the screen has no effect on the flow. In a later study Wahl (2013) refined his model and identified the angle of attack, α (Fig 3) of the approaching velocity vector, as the dominant parameter. Using regression, he related the orifice coefficient, C_cv to α and found that, for a given screen geometry there is a unique relation between the two factors. Using this, Wahl was able to improve his model, reducing the standard deviation of the relative errors between the computed and observed flows from 16.5% to 7%. The new model predicts significantly higher flows and is more accurate over a wider range of operation. These changes have been implemented in a computer model (USBR, 2015).

Other investigators [Venkataraman (1977), Nasser et al. (1980), and Ramamurthy et al. (1994)] have also related the orifice discharge coefficient to the Froude number for flow between parallel slots for a variety of flow regimes. Both one dimensional flow with an assumed hydrostatic pressure distribution and more complex free surface models have been used to predict flow characteristics with good results. However, it is important to note that these studies are for flow through parallel slots created by rectangular bars. They support the basic concept of modelling flow through parallel slots but none of these have geometries with tilted wires that create the geometric offset unique to wedge wire screens and the subsequent sheared flow. Because of this, direct comparison cannot be made to Wahl’s work and neither these nor Wahl’s work investigates flow with sediment.

Kamanbedast (2012) studied the flow through a channel bottom intake rack with parallel bars used to exclude sediment in small hydropower intake structures. The best performance for sediment exclusion occurred when the rack slope was 30% (17°) and the open area between bars was 40%. Wahl (2003) reported on screen slopes ranging from 10° to 75° and generally concludes that while unit discharge does not change considerably with screen angle, a steeper angle (closer to 45°) is better. The difference between these (17° vs 45°) can be, at least partially, explained by the importance of the flow angle of attack and high Froude numbers needed for effective Coanda screen performance.

3. Laboratory Models

A series of laboratory tests were completed to assess the efficacy of the Coanda effect screen in removing sediment. Initially, the clean water hydraulics were validated with the apparatus shown in Fig. 4. The flume has a nearly horizontal approach section and a test section set at a slope of 45°. Screens were inserted into an opening in the flume bed. Water was circulated from a tank through the flume and into either the through-flow or bypass-flow tanks before returning to the recirculation tank. For all tests the flow rate was measured with a sonic flow meter just before the flow entered the flume. Calibrated v-notched weirs were used to measure the through-flow and bypass-flow in their respective tanks. The system was operated with continuous flow.

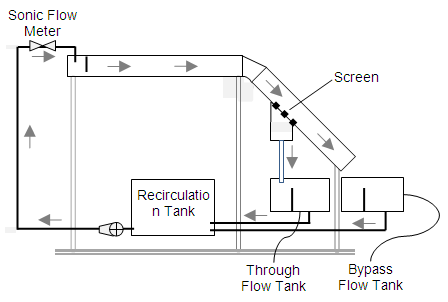Figure 4. Schematic diagram of the laboratory apparatus in continuous flow mode

3.1. Geometry of Coanda Effect Screens

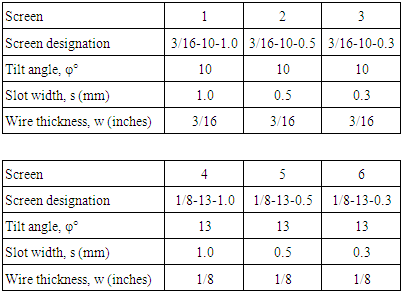
The wire tilt angle φ, face angle λ, slot width s and wire width w characterize the screen geometry and are defined in Fig. 5 and summarized for six screens in Table 1. The mixed units used by the manufacture to designate the screen are maintained here. For example the 1/8–13-0.3 screen shown in Figure 1 refers to a 1/8” wire width, 13° tilt angle and 0.3mm slot width.

Table 1. Screen geometry

Screen geometry was verified using photographic measurements. As seen in the example (Fig. 5) there is some variation in the measured angles but in general they match the nominal values reported by the manufacturers.

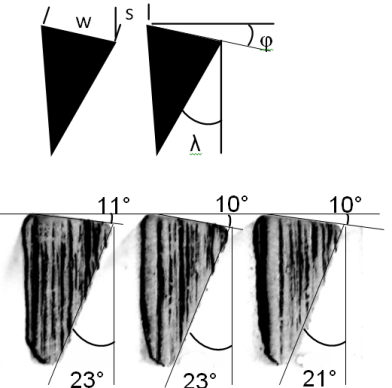Figure 5. Geometric parameters are defined in the idealized top view and confirmation of angles from photographic measurements are shown in the bottom view

3.2. Clean Water Tests

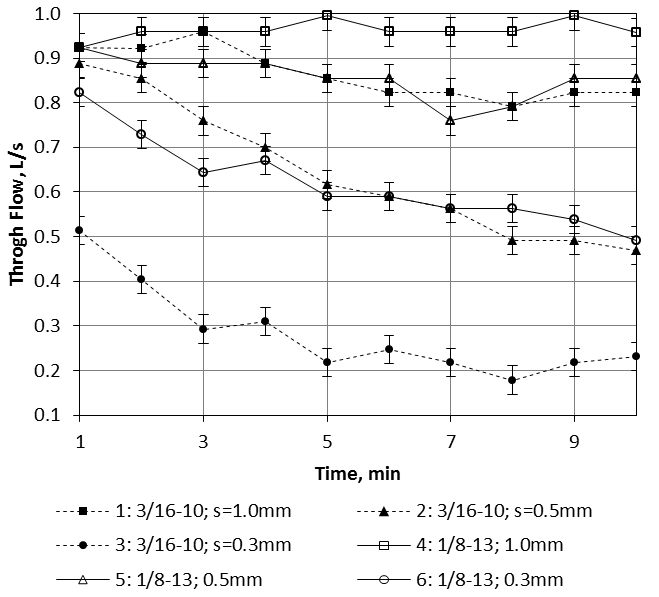
Clean water tests were run to verify the hydraulic performance. Using the laboratory apparatus (Fig 4), screens were inserted into the device and runs were made varying the inflow from 0 to about 1.26 L/s (20gpm). This is the typical range of design flows for small rural water systems in the developing world.

As expected, flow through a screen is a function of the wetted length of screen that is producing flow. Other factors, including angle of attack, wire spacing and tilt angle were studied by Wahl (2003, 2013). He found that the unit discharge was proportional to the wetted length raised to the 1.24 power (L^1.24). For screens 1, 2 and 3 the comparable relationships from this study are,

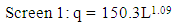(1)

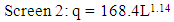(2)

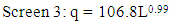(3)

where q is the discharge per unit width through the screen and L is the wetted length of the screen. The error bars for each data set (Fig 6.) are roughly the same size as the separation between the fitted trend lines. The similarity of these relationships suggests that the through-flow does not vary appreciably with slot width, s, which can be explained by considering that for any length of screen the total open area (between wires) is roughly the same. Wahl provides a thorough discussion of clean water flow through screens.

Figure 6. Screen 1 produces a typical relationship between through-flow and wetted screen length

3.3. Water and Sediment Tests

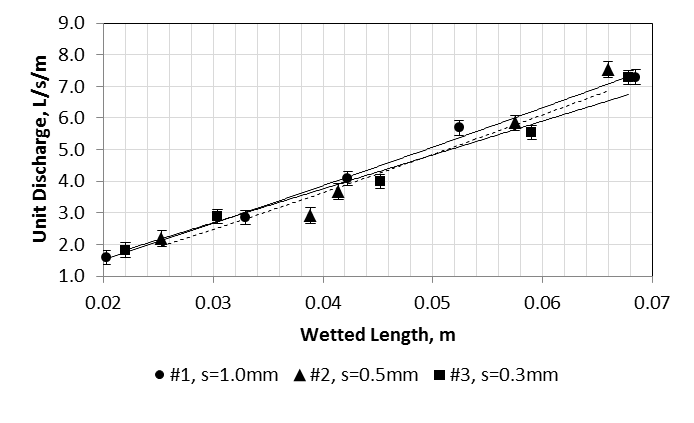
In small upland watersheds, the sediment particle size distribution and concentration varies with the local geology, hydrology, topography and land use. A sediment sample collected from a small stream in northern Nicaragua was used as a model for the particle size distribution (Fig. 7) in this study. The particles in this sample fall within the sand size range (0.0625mm to 2mm) and although smaller particles, responsible for increased turbidity, are most likely present during storm flows, they generally do not degrade the physical system and cannot be removed with Coanda effect screens. Because the Nicaragua sample included bed load, the distribution is skewed toward the larger sizes. The design mix was adjusted by increasing the fraction of smaller particles resulting in a more realistic distribution.

Sediment concentration in rivers and streams vary widely. Specific data on small streams in monsoonal regions is not available, but to get a sense of the possible range of concentrations consider that the flow weighted suspended sediment/sand concentration for 16 USGS gaging stations on the Mississippi River and its tributaries ranged from 137 mg/L to 29,900 mg/L (pre-1953) and 61.6 mg/L to 11,100 mg/L (post-1967). By 1967, most of the larger channelization projects and land-conservation practices implemented on the Mississippi River were in place resulting in the reduced sediment load (Heimann 2011). The Yellow River in China at the Sanmenxia station has one of the world’s highest recorded sediment concentrations; the long term annual average concentration is 35,000 mg/L (Wu 2004).

Figure 7. Sediment particle size distributions for a typical sample from Nicaragua and the design sediment mix used for testing

For this study a sediment concentration of approximately 25,000 mg/L was used. This represents a very high concentration and presumably will significantly exceed the actual sediment load in streams where the Coanda effect screens would be used.

To assess the efficacy of the Coanda effect screen as a sediment exclusion device the test apparatus was modified to run in batch mode (Fig 8). Sediment was injected into the flow via a hopper suspended above the flume entrance. A calibrated valve at the exit of the hopper regulated a steady flow of sediment. The system was adjusted for 10 minute batch runs at a water flow rate of approximately 0.883 L/s (14 gpm) and a concentration of 25,000 mg/L.

Figure 8. Schematic diagram of the laboratory apparatus in batch flow mode

Samples were collected at the 2, 5 and 8 minute marks from the through-flow and bypass-flow streams. The samples were dried and the sediment size distributions were determined using a standard sieve test. A simple calculation leads to the fraction of each sand size removed by the Coanda effect screen.

4. Results

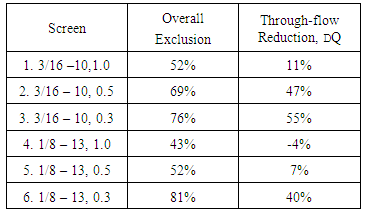
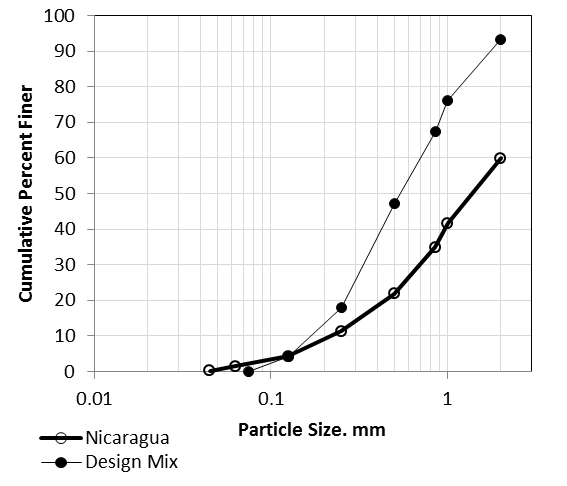
With time the space between individual wires tends to clog with sediment reducing the total flow through the screen. This is a function of the screen geometry. The 3/16-10 and 1/8-13 screens with 1.0 mm wire spacing and the 1/8-13 with a 0.5 mm spacing did a good job of self-cleaning, reaching a flow equilibrium by the end of the 10 minute batch run and maintaining a relatively high flow rate with reductions of up to 11% (Fig.9). The other screens had poorer performance exhibiting a greater reduced flow (40% - 55%) or not reaching flow equilibrium.

Figure 9. Flow through Coanda effect screens as a function of time with sediment laden water

Sediment tends to build up on a portion of the screen and then periodically it self-cleans. This episodic behaviour appears to be triggered by the increased depth of flow resulting from the accumulation of sediment that blocks flow through the screen at that location. Observations suggest that increased shear stress, due to increased depth, and possibly an increased local velocity are responsible for initiation of the self-cleaning process.

The percent of sediment excluded, as indicated in Figure 10, refers to the fraction of material that did not pass through the Coanda effect screen for that particle size interval and is a measure of the screen’s effectiveness. For example, for the 3/16-10; 1.0mm screen, 100% of the material 2.0mm or greater was excluded from the through-flow. For the particle size interval between 1.0mm and 2.0mm 100% was excluded, for the 0.85mm to 1.0mm interval 65% was excluded and so on … (0.5mm to 0.85mm - 49% for 0.25mm to 0.50mm - 32%, 0.125mm to 0.25 - 19% and 0.075 to 0.125mm - 7%). Figure 10 shows the results for all 6 screens. The accompanying reduction in equilibrium through-flow, DQ, is also listed. These results are for measurements made 8 minutes into the 10 minute batch test.

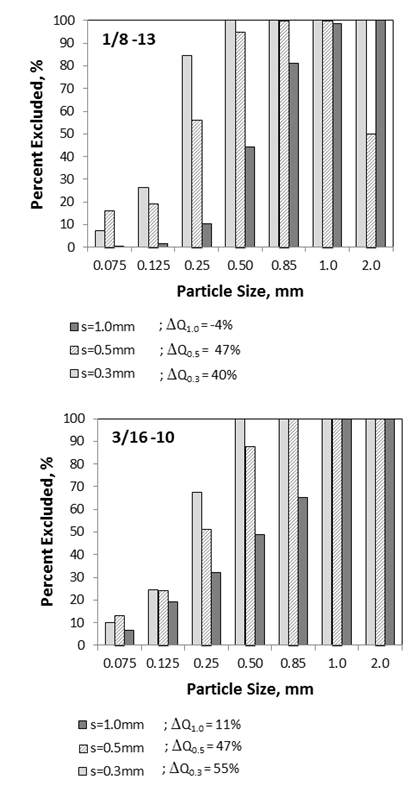Figure 10. Percent of sediment removed for each particle size interval

The total amount of sediment excluded by each screen is determined by knowing the size-interval removal rates (Fig. 10) and the portion of the sample represented by that interval (Fig. 7). For the test design mix, this resulted in overall sediment exclusion rates from 43% to 81% (Table 2).

Table 2. Total sediment excluded from the through-flow

Note that screen 4 shows an increase in through-flow of 4%. This is explained by either errors in the flow measurement or variations in the inflow during the batch test.

As the sediment distribution becomes coarser the overall exclusion rate increases. For example, if the size-interval removal rates shown in Figure 10 are applied to the Nicaragua sediment distribution (Fig 7) the overall exclusion rates for the 3/16-10 screens increase to 74%, 84% and 87% for the 1.0mm, 0.5mm and 0.3mm screens respectively.

4.1. Field Prototype

A field prototype (Fig 11.) was designed and constructed using realistic constraints commonly found in rural, developing world communities. While the laboratory model confirmed performance, the purpose of the field prototype was to assess the feasibility of implementing a Coanda effect screen structure in the field. The prototype was constructed on an irrigation ditch fed from a small river with a sediment concentration much less than that used in the laboratory tests. The structure has the same fundamental shape, size and flow capacity as the laboratory model and thus it is reasonable to assume that the hydraulic performance of the field prototype would be similar to the laboratory model.

Figure 11. Field prototype of a Coanda screen, sediment exclusion structure where H=66cm, L=66cm and W=15cm. The bottom-left photo shows debris on the screen. This debris will eventually be removed by the by-pass flow

The structure was sized for a typical installation with a maximum through-flow capacity of 1.26 L/s (20gpm). The spillway slope angle is 45°, the drop is 66cm, the horizontal length is 66cm and the channel width is 15cm. The screen is 15cm x 30cm. A range of flows could easily be accommodated by simply decreasing the screen length. The pipe, visible on the left side of the structure, transports through-flow to the downstream system.

Construction was accomplished using tools and material that are commonly available in the target communities. The material cost was $260 US and 72 man-hours of labor were required to complete construction.

Based on qualitative observations the 1/8-10; 0.5mm screen did a good job of removing both sediment and debris.

Wahl et.al. (2004) provides a discussion of operation and maintenance issues for a variety of small Coanda effect screen structures. Many of these are similar to the field prototype.

5. Conclusions

The hydraulic performance of the screens during clean water runs closely matched that found by Wahl. During sediment laden tests, screens 1, 4 and 5 met the target flow rate of 0.882 L/s (14gpm) (Table 1). The 1.0mm (1/8-13) screen 4 significantly out-performed the 1.0 mm (3/16-10) screen 1 exceeding the through-flow capacity by nearly 12% with an uncertainty that represents 4% of the flow.

While it was not possible to isolate whether the difference in performance was due to the variation in the wire width, w, or the tilt angle, φ, the results were consistent across all three wire spacings. Uniformly, the combination of larger tilt angle and smaller wire width resulted in a larger through-flow with sediment laden water. Based on geometry, the author believes that the tilt angle is the more important of the two parameters. For illustrative purposes the schematic diagram (Fig. 12) shows an exaggerated progression of increasing φ from zero in frame-a to a large value in frame-c. As φ increases the thickness of the sheared flow layer increases (shaded area below the horizontal line) improving flow performance but also adversely resulting in a narrower constriction between wires where sediment can become trapped. Finding the optimum wire tilt angle is a balance between increasing flow and reducing sediment clogging. This behavior was confirmed in the sediment runs (Fig. 9) where the screens with the 13° tilt angle out performed (higher through-flow) those with φ=10°.

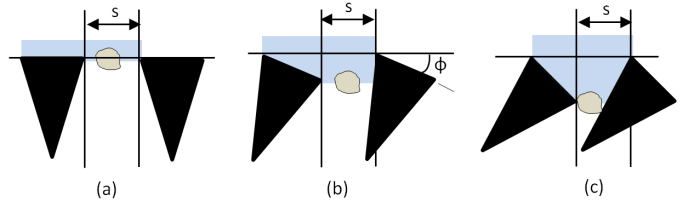Figure 12. As the wire tilt angle, φ, increases the through-flow increases but the tendency to trap sediment on the screen also increases

Clearly, screens with smaller wire spacing i.e. (s=0.3mm vs s=1.0mm) are better at removing sediment (Fig 10 and Table 2), but this comes at a cost of reduced through-flow as shown in Figure 9. As one would expect, a screen with a specific wire spacing say, s’ should remove all particles with a size greater than or equal to s’ and the data largely supports this statement. However, as a screen begins to clog and particles lodge between the wires the effective spacing decreases and particles smaller than s’ can be excluded. The corresponding cost is a reduction in flow. This is clearly reflected in Figure 10 where the smallest wire spacing is 0.3mm yet a significant fraction of particles smaller than 0.3mm are excluded. This is true for all sizes. For example, the 1.0mm screens show a removal of 40% to 50% for 0.5mm sediment.

The sediment exclusion data for each particle size interval (Fig 10.) provides a general performance measure for each screen. When this is applied to a specific sediment distribution the total sediment removal for that screen can be determined (Table 2). If the goal is to remove as much sediment as possible, then the 1/8-10; 0.3 screen 6 was the top performer with a total removal of 81%. Correspondingly this screen also had a 40% reduction in equilibrium through-flow over the duration of the test. If this screen were selected, then either a larger screen area or multiple screens would be required to achieve the target through-flow rate. The 1/8 – 10; 0.5 screen 5 is perhaps the best overall performer with a sediment exclusion of 52% and a flow reduction of only 7%. In these tests the active screen area was only 15cm by 30cm so increasing the screen size or using multiple (adjacent or stacked) screens would be a reasonable action.

The purpose of the field prototype was to assess the feasibility of implementing a Coanda effect screen for sediment exclusion in a water system intake structure in the developing world. Cost, time and difficulty of construction were considered. The prototype was successfully constructed subject to appropriate and rather stringent, real world constraints. Relying on the performance results from the laboratory model and the construction experience from the field prototype gives an accurate representation of both the efficacy and feasibility of the design and confirms the proof of concept for the use of Conada effect screens in sediment exclusion structures.

6. Recommendations

While the results are encouraging, more testing is needed to develop usable design guidelines. The relative importance of the screen geometric properties and more elaborate quantification of system performance over a wider range of operating parameters is needed. Though the relationship between unit discharge and wetted length of the screen (Fig. 6) can be used to make an initial estimate of the length of screen needed for a specific application, this relationship should be further developed using sediment laden flow and possibly varying width screens. Ultimately, relationships that could be used to provide systematic design of Coanda effects screens for sediment exclusion are needed.

ACKNOWLEDGEMENTS

This work was completed as a senior design project in the engineering program at Fort Lewis College by Justin Boren, Aaron Somogyi, Megan Chambellan and Benson Taziwa. My sincere thanks to this group of students for their work on the project. Thanks to Tony Wahl for providing valuable input. Screens for this study were graciously provided by Norris Screens and Manufacturing Inc., a part of the Elgin Equipment Group, Tazewell, Virginia and Hydroscreens CO. LLC, Denver, Colorado. Lastly, partial funding was provided by a grant from the Dean’s undergraduate research program at Fort Lewis College.