-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Hydraulic Engineering
p-ISSN: 2169-9771 e-ISSN: 2169-9801
2014; 3(3): 85-92
doi:10.5923/j.ijhe.20140303.02
On Flow Resistance Due to Vegetation in a Gravel-Bed River
Nazanin Mohammadzade Miyab1, Hossein Afzalimehr1, Vijay P. Singh2, Behzad Ghorbani3
1Department of water engineering, Isfahan University of Technology, Isfahan, Iran
2Department of Civil and Environmental Engineering, Dept. of Biological and Agricultural Engineering, Texas A&M University, USA
3Department of water engineering, Shahr-kord University, Shahr-kord, Iran
Correspondence to: Hossein Afzalimehr, Department of water engineering, Isfahan University of Technology, Isfahan, Iran.
| Email: |  |
Copyright © 2014 Scientific & Academic Publishing. All Rights Reserved.
Using hydraulic data collected in thirteen cross-sections in a 250 m long reach of Babolroud River, Iran, this study investigated the relation between flow resistance and vegetation in a gravel-bed river with vegetated banks. It was found that the maximum flow velocity occurred on the water surface for bare bank cross-sections, but near the vegetated banks the dip phenomenon was observed and the maximum velocity occurred below the water surface for vegetated cross-sections. The log law is valid at various distances from vegetated banks in gravel bed rivers with different commencement levels. The flow resistance was found to be an exponential function of the average relative roughness with the coefficient of determination 0.733. Correlation of coefficient of 0.943 was obtained by charting between relative velocity and nonlinear equation dependent on relative roughness, Reynolds number and plant inclination factor. More field investigations are needed to quantify and localization this relation.
Keywords: The log law, Flow resistance, Vegetated banks, Gravel bed
Cite this paper: Nazanin Mohammadzade Miyab, Hossein Afzalimehr, Vijay P. Singh, Behzad Ghorbani, On Flow Resistance Due to Vegetation in a Gravel-Bed River, International Journal of Hydraulic Engineering, Vol. 3 No. 3, 2014, pp. 85-92. doi: 10.5923/j.ijhe.20140303.02.
Article Outline
1. Introduction
- Ecological and aesthetic values have become an integral part of modern river management, and therein natural riverbank and floodplain vegetation plays major role. In recent years, river restoration has become an accepted practice in many countries [1]. In this regard, softer alternatives to earlier engineering solutions, such as bioengineering, are being increasingly preferred. Of fundamental importance in river restoration is the assessment of flow resistance caused by vegetation [2].Vegetation, in general, is a controlling factor in the interaction of flow, erosion and geomorphology in rivers and may cause difficulties in hydraulic design. Vegetation along rivers and in floodplains consumes a great amount of energy and momentum from the flow, and is often found to be in the region with most roughness [3]. The transfer of momentum causing shear stress on channel walls influences the main channel flow and floodplains as well as erosion and the stability of banks [4]. Masterman and Thorne (1992) pointed out that bank vegetation is a key factor in reducing flow velocity [5].Interactions between flow and vegetation are complex and depend on environmental factors and plant characteristics, such as mean flow velocity, turbulence, channel morphology, water temperature, plant morphology, age and size, and the spatial distribution of plant patches [6].Many investigations have already been undertaken to describe the relationship between flow resistances, Manning’s n, or drag coefficient (Cd), with the type and spatial distribution of vegetation. Analytical and experimental studies of vegetation-related resistance to flow depend on relative submergence [7]. Also, plant characteristics, such as leafs and bending, may have an important influence on the flow resistance ([2], [8]).The chart below shows that flow resistance depends on many factors.The definitive quantitative relation between flow resistance and controlling parameters (predictor parameters) is a long-standing problem in hydraulics and remains unclear as yet [9]. A rigorous approach for deriving hydraulic resistance relationships is based on the integration of the double-averaged (in time and space) Navier–Stokes equations [10]. However, it is not an easy task to quantify the contribution of all predictor parameters in the flow resistance equation by Navier–Stokes equations. Among simplified approaches which are currently applied, two methods are promising. The first method was suggested by Kouwen et al. as follows:
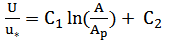 | (1) |
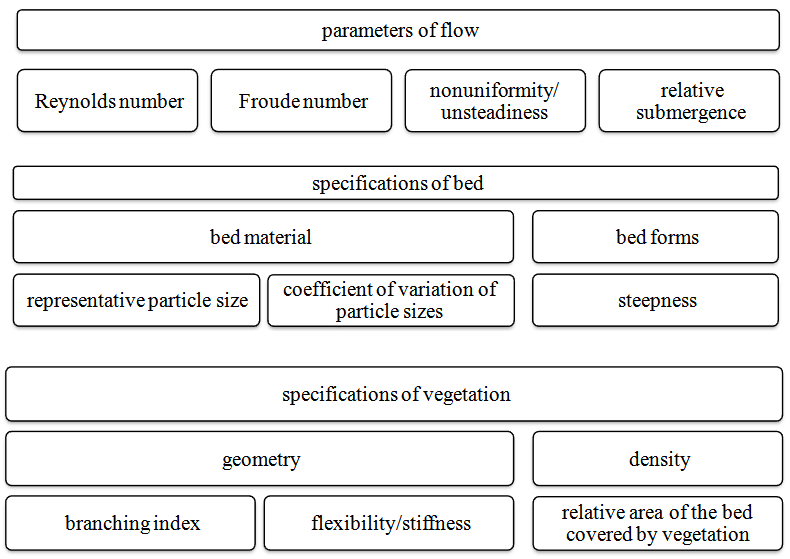 | Figure 1. Chart showing parameters affecting flow resistance estimation |
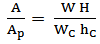 | (2) |
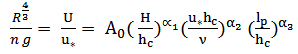 | (3) |
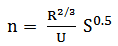 | (4a) |
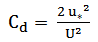 | (4b) |
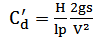 | (4c) |
2. Experimental Setup
- A reach of Babolroud River was selected for field experiments. The river is located near the city of Babol in north of Iran, near the Caspian Sea. The reach was 250 m long with 13 measured cross sections where 11 cross sections of which are with vegetation on banks and 2 cross sections of which are with bare banks. Figure 2 presents a plan of selected reach.
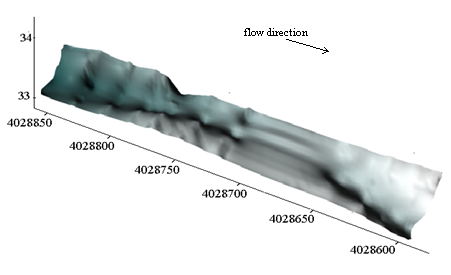 | Figure 2. Plan of the selected reach |
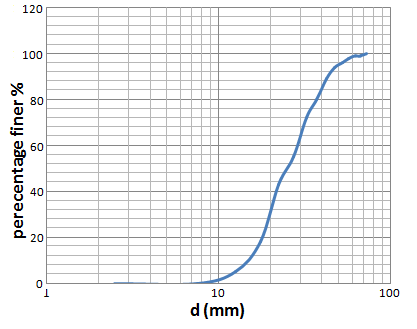 | Figure 3. Grain size distribution of bed material |
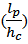 between 1.5-3.
between 1.5-3. | Figure 4. Image of vegetation along river banks |
 | Figure 5. Current-meter used in this study |
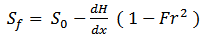 | (5) |
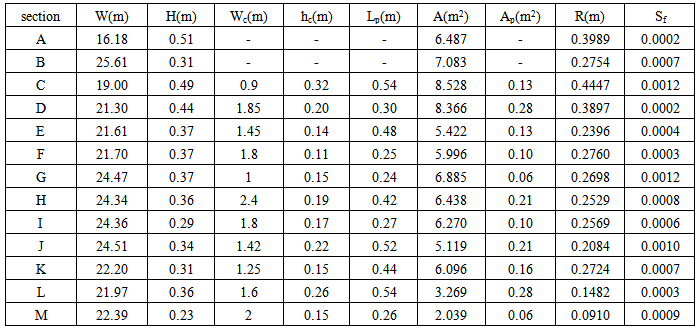
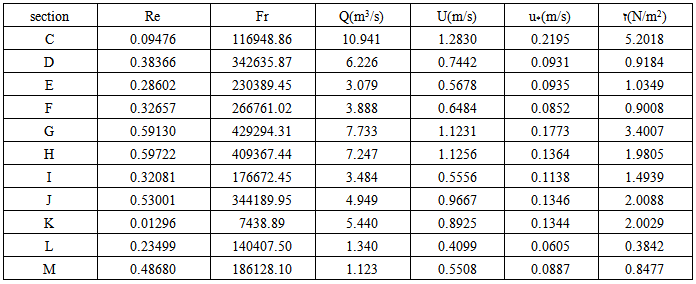
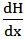 is the flow depth variation and Fr is the average of Froude number at each cross section. The range of width and depth of the reach is from 17.5 to 25.6 meters and 0.14 to 0.65 m, respectively. Discharge was calculated by using the continuity equation Q = A × V, where A is the cross section area, and V is the weighted velocity in each section.Table 1 presents a summary of experimental and calculated data for 13cross-sections along the selected reach, where Wc and hc present the weighted values.No vegetation cover was observed at the sections of A and B, that is why no value was reported for Wc, hc, Lp and Ap at these sections.
is the flow depth variation and Fr is the average of Froude number at each cross section. The range of width and depth of the reach is from 17.5 to 25.6 meters and 0.14 to 0.65 m, respectively. Discharge was calculated by using the continuity equation Q = A × V, where A is the cross section area, and V is the weighted velocity in each section.Table 1 presents a summary of experimental and calculated data for 13cross-sections along the selected reach, where Wc and hc present the weighted values.No vegetation cover was observed at the sections of A and B, that is why no value was reported for Wc, hc, Lp and Ap at these sections.
|
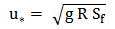 | (6) |
|
3. Results
3.1. Velocity Distribution
- Considering the range of river width in table 1, the aspect ratio (Wc / hc) changes with an interval of 26-100 with an average of 80. Figure 6 shows measured dimensionless velocity profiles in which the maximum flow velocity occurs at the water surface for the bare banks sections, however, near the vegetated banks the dip phenomenon is observed in which the maximum flow velocity is below the water surface. Also, the application of the log law is presented for each velocity profile in Figure 6.
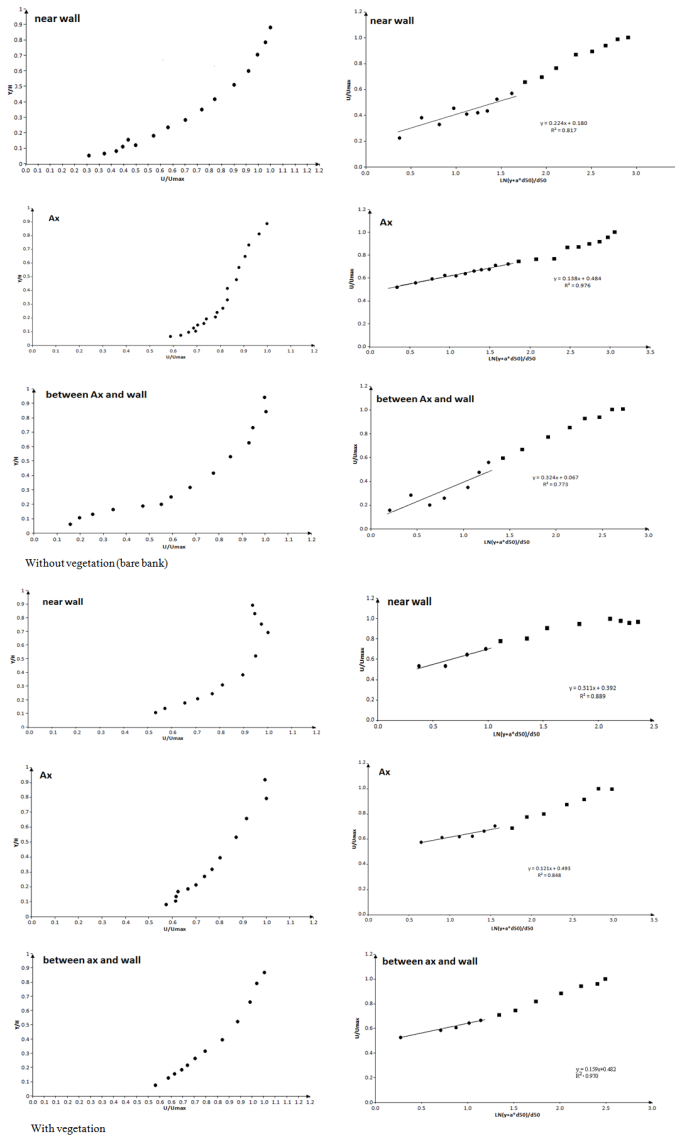 | Figure 6. Velocity distribution and log law application for bare banks and vegetated banks sections |
 | (7) |
3.2. Flow Resistance Estimation
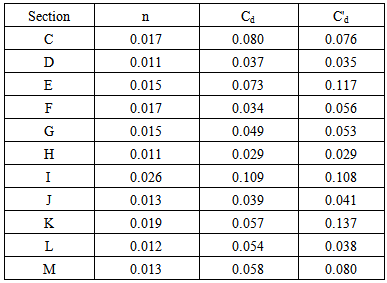
- The flow resistance was determined using equations (4). Results of the weighted values of the Manning coefficient (n), drag coefficient (Cd) and bulk drag coefficient are presented in table 3.
|
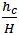 , plant inclination factor
, plant inclination factor 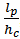 , and areal vegetation cover
, and areal vegetation cover 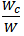 [17].In the studies of Kouwen (1969), Watson (1987), Barky et al. (1992), Champion and Tanner (2000) and Green (2005a), the site average relative roughness
[17].In the studies of Kouwen (1969), Watson (1987), Barky et al. (1992), Champion and Tanner (2000) and Green (2005a), the site average relative roughness 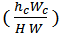 was adequate to predict the flow resistance. Therefore, it was selected for this study ([9], [11], [18], [19]).Using a statistical analysis of resistance coefficients and
was adequate to predict the flow resistance. Therefore, it was selected for this study ([9], [11], [18], [19]).Using a statistical analysis of resistance coefficients and 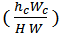 , it was found that the best correlation with a range of R2 0.733 revealed an exponential function.
, it was found that the best correlation with a range of R2 0.733 revealed an exponential function.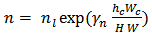 | (8a) |
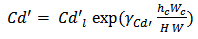 | (8b) |
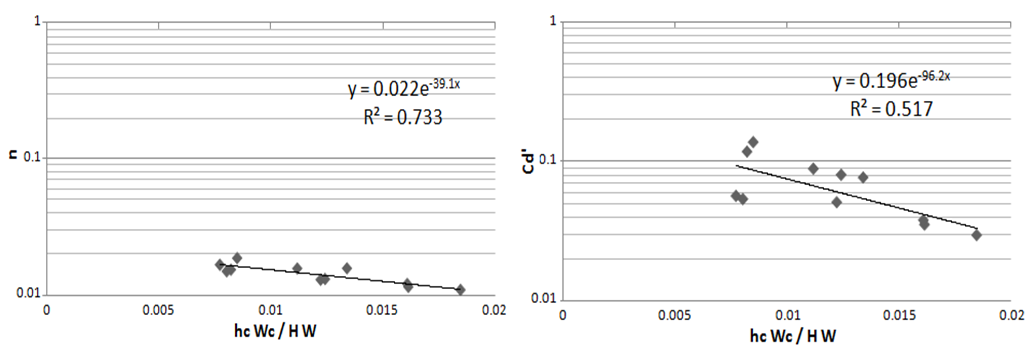 | Figure 7. Exponential relations of flow resistance |
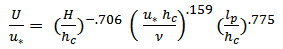 | (9) |
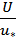 and
and 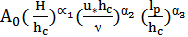 were achieved as A0 that drawing the plot for cross sections was in the form of linear sub contrariety with R2 = 0.943 (figure 8).
were achieved as A0 that drawing the plot for cross sections was in the form of linear sub contrariety with R2 = 0.943 (figure 8).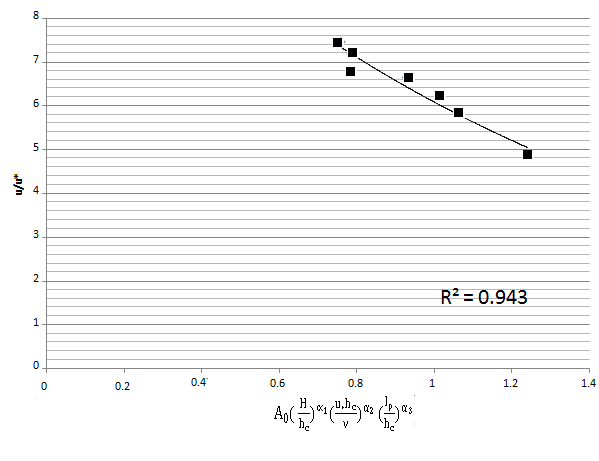 | Figure 8. Flow resistance presentation |
4. Conclusions
- The following conclusions are drawn from this filed study:1. The aspect ratio varies from 26 to 100 with an average of 80 showing the larger aspect ratio, the smaller is Manning coefficient.2. The maximum flow velocity occurs at the water surface for the bare banks sections, but near the vegetated banks the dip phenomenon is observed and the maximum flow velocity occurs below the water surface.3. Vegetation on river banks affects the thickness of log law zone where the log-law is applicable, showing this law can be applied at various distances from vegetated banks in gravel-bed rivers with different commencement levels.4. The relation between the Manning roughness coefficient (n) and average relative roughness was found to be exponential, with the coefficient of determination of 0.733. 5. For grass with low stem density, the relation between relative velocity and characteristic parameters of relative roughness, Reynolds number and plant inclination factor was significant with the coefficient of determination of 0.943. More data are required to calibrate and validate the findings of this research.
Notation

 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML