Madjid Delkash, Babak Ebrazi Bakhshayesh
Department of Civil and Environmental Engineering, University of Delaware, Newark, USA
Correspondence to: Madjid Delkash, Department of Civil and Environmental Engineering, University of Delaware, Newark, USA.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
Side weir is a popular hydraulic structure used widely in drainage and irrigation systems and wastewater treatment plants. This paper probes some well-known discharge coefficient equations to assess the condition of validation and accuracy for each. In order to achieve this goal, 193 tests were run. 15 well-known equations presented in table 1 were meticulously investigated to examine their accuracy. Despite DeMarchi’s assumptions, the results reveal that specific energy is not constant along lateral weir and ignoring its gradient along lateral weir is not reasonable. Further investigation renders gradient of specific energy greater than water profile gradient along this weir in some cases; therefore this paper presents a discharge coefficient equation appropriate for mentioned condition.
Keywords:
Side weir, Discharge coefficient, DeMarchi equation, Common discharge equation of weir
Cite this paper: Madjid Delkash, Babak Ebrazi Bakhshayesh, An Examination of Rectangular Side Weir Discharge Coefficient Equations under Subcritical Condition, International Journal of Hydraulic Engineering, Vol. 3 No. 1, 2014, pp. 24-34. doi: 10.5923/j.ijhe.20140301.03.
1. Introduction
Side weir is built on the side of a main channel andfree spatially varied flow with decreasing discharge is the dominant regime over this hydraulic structure. Its mechanism is deviation of water from straight direction and sending it to side weir. Decreasing the ultimate (downstream) discharge in main channel is the result of this action. It means, if a flow with discharge (Q1) crosses a side weir, its discharge will be reduced (Q2) because of spilling over side weir (Qw). As observed and represented in Fig.1 for subcritical condition, the depth of water increases while passing side weir.While side weir plays a vital role in several systems, there is no exact, comprehensive and analytical solution for it.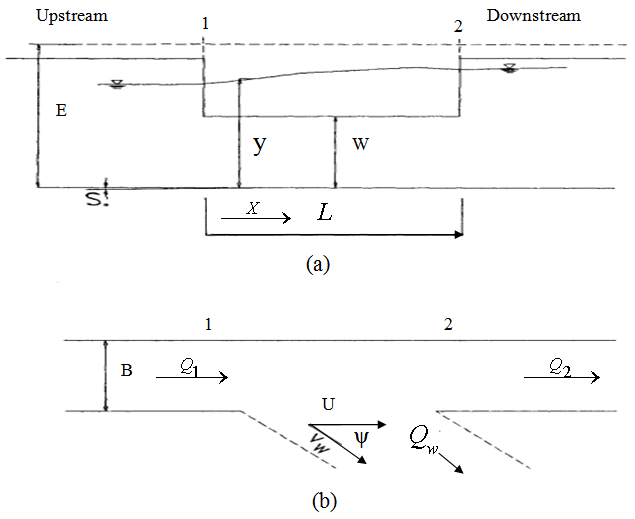 | Figure 1. Scheme of a side weir (a) lateral (b) plan view |
Specific energy in rectangular channeldefinedin terms of equation (1) is the key to solve some hydraulic problems such as determination of side weir’s discharge.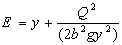 | (1) |
where E is specific energy, y is the depth of water, Q is the discharge of fluid, g is the gravitational constant and b is the width of main channel.A considerable number of studies have been conducted to improve the knowledge about this complicated hydraulic structure since previous century. Kindsvater and Carter (11), examined the role of surface tension as a function of the ratio of head of the water to the weir height. Some researches addressed the experimental results to generate the discharge coefficient[1, 5, 9, 13, 17, 19]. Some scientists believed that constant momentum along lateral weir is the correct assumption[4]. On the other hand, several works asserted that constant specific energy along it is a better assumption. This paper searches among the second group studies.Equation (2) displays the common formula used for weirs and is derived based on some assumptions. It is crucial to calculate discharge coefficient (Cm) to obtain the discharge of side weir. This coefficient mainly hinges on Froude number, ratio of the length of the side weir to the width of the main channel, ratio of the water depth to the height of the weir and angle of deviation. The deflection angle of water flow is defined by equation (3) to (5). The dimensionless ratio length of side weir to width of main channel (L/b) implies the effect of deflection angle, so this parameter (Ψ) is not considered in discharge coefficient equation (4).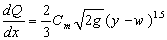 | (2) |
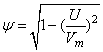 | (3) |
where Cm is discharge coefficient of weir, x is the axis along this weir, U and Vw are the abbreviations of velocity of main channel and spilling flow, Ψ the angle of deviation (Cos Ψ = 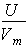 in Fig.1-b) and w is the height of side weir.Combination of equations (1) and (2) yields the equation (4). Moreover, it is evident that equation (5) is the other form of equation (1).
in Fig.1-b) and w is the height of side weir.Combination of equations (1) and (2) yields the equation (4). Moreover, it is evident that equation (5) is the other form of equation (1). 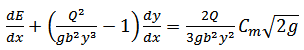 | (4) |
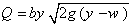 | (5) |
Now merging equations (4) and (5) produces equation (6).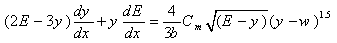 | (6) |
DeMarchi (3), made some assumptions which solved the flow over side weir analytically. Ignoring the friction and assuming constant specific energy along lateral weir are the main assumptions made by him. Based on these assumptions, he presented the equation (1) by solving analytically[6;18]. DeMarchi supposed constant specific energy along the side weir (dE/dX=0), so he eliminated the secondterm of left side of the equation (6) and that led to his famous equation shown as equation (7) where subscripts 1,2 indicate the upstream and downstream conditions respectively.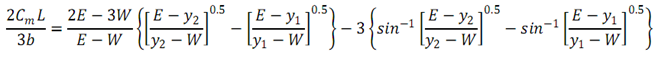 | (7) |
where L is the length of side weir.Various investigations have been done to identify the side weir discharge coefficient. These researches investigated the rectangular side weir under subcritical flow. Looking at these equations reveals that they have different values for same hydraulic flow configurations. In addition, some of them are function of Froude number only, while the others are function of L/B and W/y too. Table 1 is the excerpt of the several researchers’ former effortsordered chronologically. Obviously, only Froude number was prevalent in most earlier equations, while the later ones involve other effective elementsdetermining discharge coefficient such as (L/b, y/W) too. Table 1. Discharge coefficient equation surveyed in this review
 |
| |
|
Glimpsing at table 1 expresses that there is no same trend in dealing with side weir discharge coefficient and there are several equations whose applications are not clear. It seems crucial to study that which equation has the most validity and finding out the governing conditions for each equation. By the way, it is interesting to examine the importance of each non-dimensional number in discharge coefficient at various hydraulic circumstances. Literature is overwhelmed with side weir discharge equations and the first question sticks in mind is that why there are many equations for this side weir. If they stem from one origin, why there is no certain equation. It seems that something is wrong about them and the origin of these equations, equation 6, will be surveyed based on order of magnitude latter, then an analytical solution will be applied in order to illuminate the accuracy of DeMarchi’s assumptions. Moreover, no investigation has been reported about examining the side weir discharge coefficient up to now. It is important to point out that since there is lack of well-knit research done in this regard, the decisions made about side weir discharge coefficient is not based on scientific decision.Nevertheless, it sounds essential to share the direct observations and results of experiments to develop a reliable source for decision making and estimation of side weir discharge coefficient. This paper aims at clarifying which equations indicated for side weir discharge coefficient have the most applicability and accuracy among well-known equations presented in Table 1 and introduce the appropriate discharge equation (DeMarchi equation or common equation) for specific hydraulic and geometry conditions (Froude number, the ratio of side weir length to main channel width and the depth of water to the height of side weir). Furthermore, analytical approach was spotted to illuminate why DeMarchi equation is not valid in some cases and finally a new equation will be dedicated for its appropriate condition.
2. Materials and Methods
2.1. Data Description and Facilities
About 193 tests including various ranges of the hydraulic and geometric parameterswere run for this investigation. Table (2) displays all the information about set up of these tests.| Table 2. Data description |
| | Parameters | Values | | Length of side weir (cm) | 20,30,45,75 | | Height of side weir(cm) | 1,10,19 | | Slope of channel(%) | -0.5,0,0.5,1 | | Discharge(lit per sec) | 35-100 | | Froude number | 0.1-0.8 | | Number of tests | 193 |
|
|
The flume used for these tests has 12 (m) length, 0.3(m) width and 0.5(depth). The side weir employed in this flume was constructed by plexiglass and 2 standard weirs measuring discharge were established at the beginning and end of the channel, also 2 piezometers were installed to measure water depth (Fig.2). Any further descriptions about experimental setup can be found in Borghei et al,[1].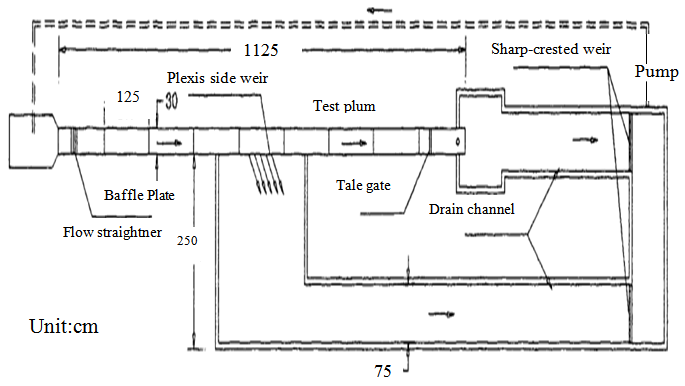 | Figure 2. Plan of experimental setup |
2.2. Methodology
To find out that which equation is the most fitted for which condition the main assumption of side weir under subcritical condition was considered (Constant specific energy between up and down stream). Both DeMarchi’s equation (7) and common discharge equation (2) were taken into account as another equation to obtain the two unknowns (y2 and Q2), because it was not explicitly mentioned in literature that these discharge coefficient equations were recommended for either DeMarchi equation or common equation. These two equations (constant specific energy and once DeMarchi’s and then common equation) were solved simultaneously to determine the downstream discharge and depth(Q2 and y2). Getting the downstream discharge leads us to finding the discharge passing over side weir for taking DeMarchi or common equations (Qs=Q1-Q2). Comparing the side weir calculated by taking DeMarchi’s equation or common equation against the observed side weir discharge declares the better equation should be used in. This procedure was repeatedfor all the presented equations in Table 1. Dividing known effective parameters (Fr, w/y and L/b) to several intervals paves the way for interpretation, thereforethe Froude number is broken down to (0.2-0.3), (0.3-0.4), (0.4-0.6) and (0.6-0.8), while the ratio of length of side weir to width of channel is disintegrated to 0.67,1 and 2.5. Jalili and Borghei[1], attested that the ratio of the depth of water to the height of side weir (y/w) has a reverse effect on discharge coefficient, the values of W as indicated in table 2 are 10,19 and 190 (cm).
3. Results and Analytical Equation
3.1. Results
According to table 1, Froude number prevails in most of the equations.Ramamurthy and Carballada[14] stated that the ratio of the length of side weir to width of main channel played an inevitable role in determining discharge coefficient. Singh et al.[16], believed that the ratio of height of the side weir to depth of water affected the discharge coefficient.The criteria being the best equation are defined in terms of a low R.M.S.E.(Root Mean Square Error) and the best regression simultaneously. It means that the least value of RMSE and closest regression value (slope) to one were taken into account as the best equation. If there were more than one equation, or two equations with similar RMSEs and slopes of regression, the 95% confidence level was considered to find out the best equation. As the 95% confidence level decreases, the statistical relation between two discharge data is much significant. In some cases, there are no significant statistical differences between two data sets, so both of them were introduced as appropriate equations. 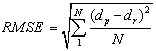 | (8) |
where 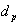 stands for predicted value and
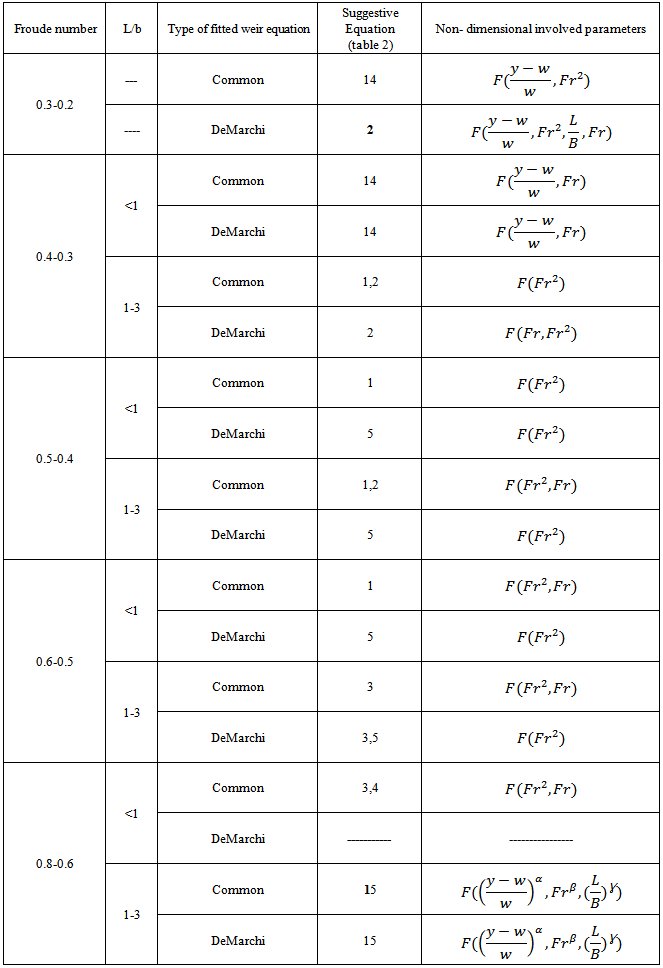
stands for predicted value and 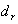 is representative of observed values and N is the number of data. The volume of results is beyond this paper, this methodology was implemented for all the subdivision conditions defined previously and the best results are reported in table (3). The table represents the best equation for any condition (Froude number, the ratio of side weir length to main channel width and the depth of water to the height of side weir).
is representative of observed values and N is the number of data. The volume of results is beyond this paper, this methodology was implemented for all the subdivision conditions defined previously and the best results are reported in table (3). The table represents the best equation for any condition (Froude number, the ratio of side weir length to main channel width and the depth of water to the height of side weir).Table 3. Suggestive equations for any condition
 |
| |
|
3.2. Analytical Survey of DeMarchi Equation
As the results corroborate, the DeMarchi equation does not operate properly under some conditions, thusit is attempted to explore the causes here. To this end, first the validity of his assumptions is meticulously investigated. In equation (6), DeMarchi ignored the gradient of specific energy along lateral weir. In order to assess this assumption the order of magnitude of the first and second terms in left side of the equation (6) was compared. Since the differentiation of specific energy and water depth with respect to x direction are unknown, so the linear differentiations are the substitution of them. It signifies that the ratio of the subtraction of the upstream from downstream values to the length of side weir is representative of differentiation. The results show only in less than 10% of cases the second term in the left side of the equation (6) is negligible by comparison with the first term, so this eliminationis not reasonable and will render inevitable error. In other word, DeMarchi supposed inequalityshown below would govern over side weir.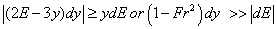 | (9) |
DeMarchi assumption will be correct, provided that the above inequality comes true. As one answer for it, the condition whose Froude number urges to zero and differentiationof specific energy is less than water depth counterpart can be considered. To dive into abyss a new non-dimensional parameter is defined: differentiation of specific energy with respect to water depth (dE/dy).The sensibility of this parameter to Froude number in DeMarchi assumption can be deduced by equation (9), so the sensibility to other parameters is discussed here. Base on inequality (9), when dE/dy is higher than one, DeMarchi equation is not valid. With regard to Fig.3, the ratio of side weir length to main channel width(L/b) has a reverse effect on this ratio(dE/dy). Governing DeMarchi’s assumption, conservation of specific energy, needs the less than1 vertical value, although most of them do not obey this assumption. Figure 3 reveals that this assumption is not comprehensive.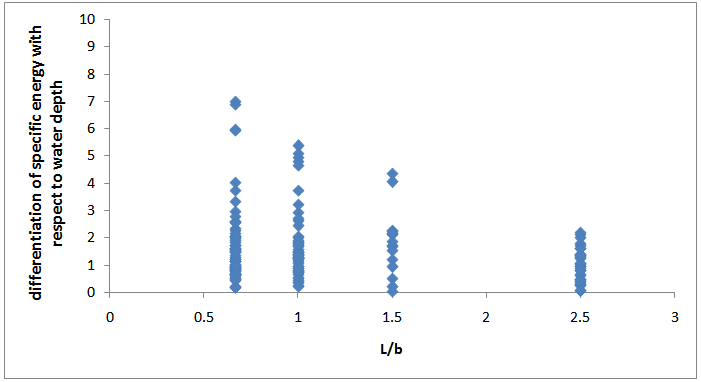 | Figure 3. Differentiation of specific energy with respect to water depth versus L/b |
The other effective parameter, i.e., the height of side weir, is considered in Fig.4. Thisfigure represents the trend of dE/dyagainst the height of side weir. It is extractable that the more height of side weir leads to the more dE/dy, which denies DeMarchi assumption for side weir with higher heights. Furthermore,no explicit trend between dE/dy and the ratio of the depth of water to the height of side weir (W/y) was observed.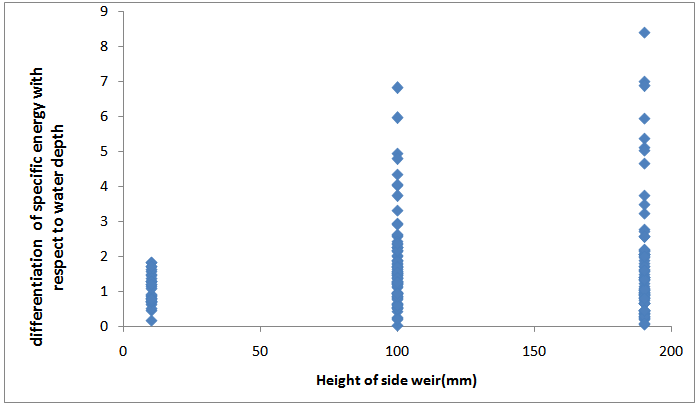 | Figure 4. Differentiating of specific energy with respect to water depth versus height of side weir |
Considering the figure of specific energy versus water depth (Fig.5) reveals that the dE/dyreduces as the flow get closer to critical condition, therefore another parameter helping us illuminate the reasons of deficiency of De Marchi equation is introduced as((E1-Ec)/(E2-Ec)). So it can be deduced that his assumption is not reliable in flow with a far specific energy from critical counterpart(E>>Ec).(E1>E2 and y12) are the proved facts about subcritical flow passing side weir, thus if we turn to Fig.5, this transverse of flow seems like a transition from point 1 to point 2. On the other hand, based on inequality (9) and Fig.5 for deeper flow, (dE/dy) urges to one (the gradient of this function is one at infinite depth), meanwhile in this condition Fr≈0 (E is equal to y, thus the velocity is negligible) so the inequality (9) is not determined because both of them are urged to zero. 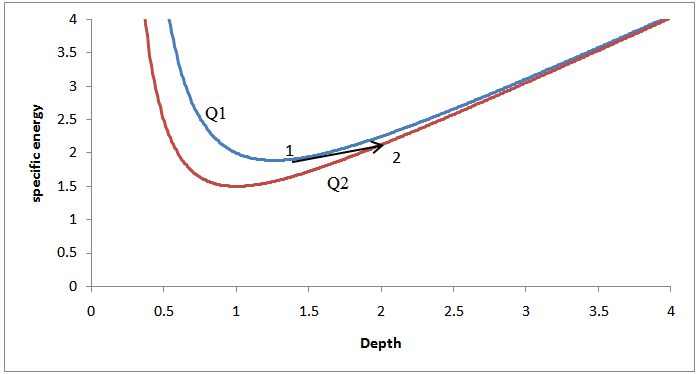 | Figure 5. Depth of flow vs. specific energy |
Beside, Fig.6 expresses when ((E1-Ec)/(E2-Ec))=1 the value of (dE/dy) can be greater than 1 and it fails the validity of inequality (9). This limit urges to 1 for infinite specific energy and higher value of ((E1-Ec)/(E2-Ec)) denotes proximity to critical flow condition. For critical condition it can be noted that Froude number tends to one, thus, dE/dy is about 1.5(E=1.5y) and fails the validity of DeMarchi assumption. As a result, DeMarchi assumption is governed in medium value of specific energy (far from critical and infinite values). 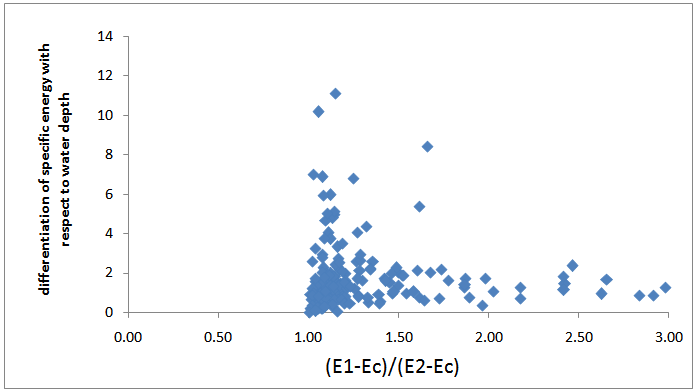 | Figure 6. Differentiating of specific energy with respect to water depth versus ratio of differences of E1,E2 from critical E |
Literature is overwhelmed with the constant specific energy assumption for flow passing side weir[1, 12]. The experiments run in this paper approve the abovementioned fact because the average of relative specific energy variation is 0.04 with standard deviation 0.03 here. But the ignored point is that assuming constant specific energy is not sufficient to ignore the (dE) in equation(6), because the (dE) is multiplied by a factor and moreover, comparing order of magnitude is essential to eliminate the energy term variation in equation (6). Turning to equation (6), order of magnitude of first to second term is dependent on dE/dy. It was shown in figures 3 and 4 that dE/dy varies as (L/b) and (W) alters. So, for several tests the first term in left side isnegligible by comparison with the second term according to the order of magnitude. This phenomenon is dominant here when the L/b is low (0.67) and W is high(190mm). So for these conditions, equation (6) can be solved analytically and equation (10) will be generated. In order to solve equation (6), the first term was ignored and the ordinary differential equation(ODE) was produced as equation(10). 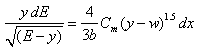 | (10) |
Solving ODE equation (10) renders equation (11) as a new solution for the oppositeDeMarchi’s assumed condition.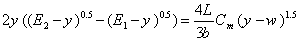 | (11) |
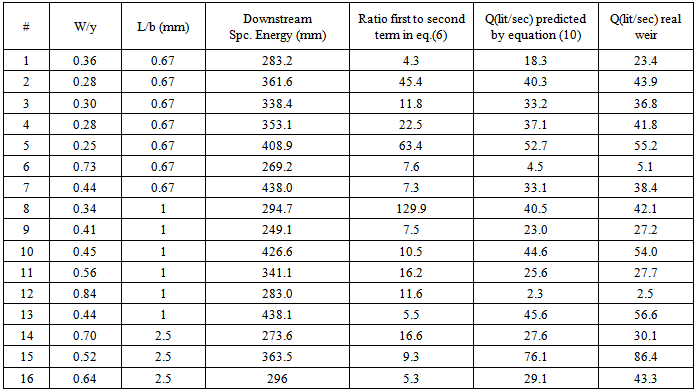
The above equation implies that water depth is constant while this assumption is not completely valid for each condition. It is worthy to note that the ratio of second term to first one of equation (6) is between 0.5-2 in majority. In other words, ignoring is not reasonable and analytical solving without any negligence for equation (6) is essential to get anaccurate and comprehensive answer.In order to evaluate equation(11), 16 tests satisfying the assumptions defined in terms of abovementioned conditionswere run. The geometry and hydraulic configurations of these tests are displayed in Table 4. As it can be seen in figures 3 and 4, ignoring the terms in equation (6) is associated with the orders of magnitude varying for each experiment. For instance, it can be inferred that equation (11) would be much reliable in higher weir height based on figure 4, while low values of (dE/dy) were observed at this condition too. It is not clear that when the validity of this equation is undermined. It renders that there are some complexity in this regard. So regarding orders of magnitude, there are some significant errors in the presented equation (11) which can be referred to complicated relation between parameters and discharge, turbulence and probable synergic relation between mentioned parameters. But generally, the introduced equation can estimate the discharge well (about 10% error).Table 4. 16tests run for evaluating the accuracy of Eq.(11)
 |
| |
|
As Fig.7 displays,the trendline shows the accuracy level of equationfor debated condition. This figure indicates the results of some tests whose second term is four times greater than first term. As the ratio of second term to first term in left hand of equation (6) increases, this figure is more fitted to bisector line (45º) reflecting the equality of measured and predicted discharge.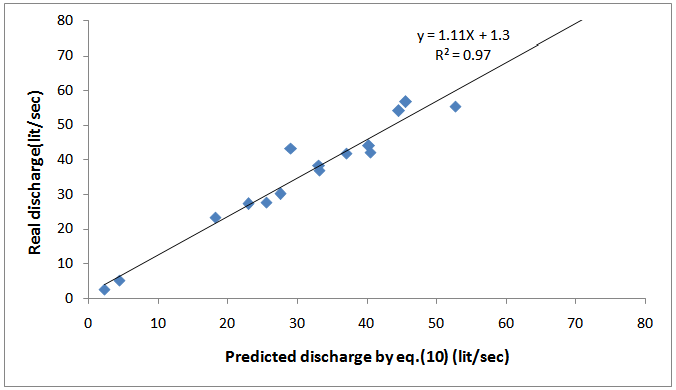 | Figure 7. Goodness of presented equation(11) for mentioned condition |
4. Conclusions
In this paper several discharge coefficient equations were investigated and the suitable condition for using them was found out, table3captures all these conditions. An analytical review of DeMarchi equation substantiates that his assumptions are not entirely validand there are several cases refuting his assumptions. This paper introduces another suitable discharge coefficient when the differentiation of specific energy with respect to water depth is higher than 1 or generally whenever inequality[9] is not compatible with DeMarchi’s assumptions and the paper verifies the accuracy of it.
ACKNOWLEDGEMENTS
The author gratefully acknowledges the assistance of Professor Borghei, deceased Professor in Sharif University of Technology, Tehran, Iran.
Nomenclature
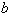 : Width of main channel
: Width of main channel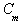 : Discharge coefficient
: Discharge coefficient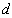 : Data used for statistical operations
: Data used for statistical operations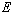 : Specific energy of water
: Specific energy of water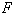 : Unknown function
: Unknown function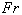 : Froude number (=
: Froude number (=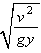 )
)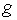 : Gravitational acceleration (m/s²)
: Gravitational acceleration (m/s²)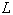 : Length of the side weir
: Length of the side weir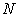 : Number of data used in statistical operations
: Number of data used in statistical operations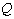 : Discharge of water
: Discharge of water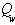 : discharge passing weir
: discharge passing weir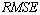 : Root Mean Square Error (equation 8)
: Root Mean Square Error (equation 8)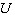 : Velocity in main direction
: Velocity in main direction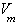 : Total Velocity
: Total Velocity 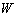 : Height of side weir
: Height of side weir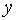 : Depth of water
: Depth of water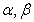 : Constants used in discharge coefficient equations
: Constants used in discharge coefficient equations
Subscript
1,2 and c= upstream, downstream and critical conditions, respectivelyp,r= predicted and real values, respectively
References
| [1] | Borghei M, Jalili MR, Ghodsian M.D is charge coefficient for sharp-crested side weir in subcritical flow. ASCE Journal of Hydraulics Engineering 1999;125(10):1051-6. |
| [2] | Cheong, HF.Discharge coefficient of lateral diversion from trapezoidal channel”, Journal of Hydrological Engineering, ASCE1991;117(4): 461-475. |
| [3] | De-Marchi, G.Essay on the performance of lateral weirs. L’ Energia Elettrica, Milan1934:11(11); 849-860(in Italian). |
| [4] | El-Khashab A, and Smith, KVH. Experimental investigation of flow over side weirs. ASCE Journal Hydrological Engineering 1976;102(9),1255-1268. |
| [5] | Emiroglu ME, Agacciouglu H, Kaya N. Discharge of rectangular side weir in straight open channels. Flow measurement and Instrumentation 2011;22:319-330. |
| [6] | Ghodsian (sabze Ali) Masoud. Analysis of side weirs and side sluice Gates. Ph.D. Thesis, University of Roorlee.India 1993. |
| [7] | Ghodsian M. Rectangular side weir analysis using elementary Discharge Coefficient. 4th International Conference on civil engineering. Tehran, Iran, 1997 May 4-6 (In Persian). |
| [8] | Hager, WH. Lateral out flow over side weir. ASCE Journal of Hydrological Engineering 1987;113(4): 491-504. |
| [9] | Jalili, MR and Borghei, SM, Ghodsian M. Discharge coefficient of rectangular side weirs. 4th International Conference on civil engineering. Tehran, Iran, 1997 May 4-6 (In Persian). |
| [10] | Jalili, MR, Borghei, SM. Discussion of discharge coefficient of rectangular side weir, by R. Singh, D. Manivnnan, and T. Satyanarayana. ASCE Journal of Irrigation and Drainage Engineering 1996;122(2):132. |
| [11] | Kindsvater CE, Carter RW. Discharge characteristics of rectangular thin-plate weirs. ASCE Journal of Hydraulic division 1957;83(6):1-36. |
| [12] | Mwafaq Y. Mohammed, Ahmed Y. Mohammed. Discharge coefficient for an inclined side weir crest using a constant energy approach, Flow Measurement and Instrumentation, Vol. 22, 2011, pp. 495-499. |
| [13] | Nadesamoorthy T, Thomson A. Discussion of spatially varied flow over side weir. ASCE Journal of the Hydraulics division 1972;98(12):2234-5. |
| [14] | Ramamurthy AS, Carballada L. Lateral weir flow model. ASCE Journal of Irrigation and Drainage Engineering 1980; 106(1):9-25. |
| [15] | Ranga Raju KG, Prasad B, and Gupta S. K. Side Weir in Rectangular Channel. ASCE Journal of Hydrological Engineering, 1979;105 (5):547-554. |
| [16] | Singh R, Manivnnan D, and Satyanarayana T. Discharge coefficient of rectangular side weirs. ASCE Journal of Irrigation and Drainage Engineering 1994;120(4):814-9. |
| [17] | Subramanya K, and Awasthy S C. Spatially varied flow over side weirs. ASCE Journal of Hydrological Engineering 1957; 98(11): 2046-2048. |
| [18] | Swamee PK, pathak SK, Mohan M, Agrawal SK, Ali MS. Subcritical flow over rectangular side weir. ASCE Journal of Hydrological Engineering 1994;120(1):212-217. |
| [19] | Yu–Tech L. Spatially varied flow over side weirs. ASCE Journal of Hydrological Engineering 1972; 98(11):2046- 2048. |


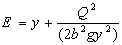
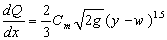
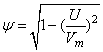
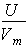 in Fig.1-b) and w is the height of side weir.Combination of equations (1) and (2) yields the equation (4). Moreover, it is evident that equation (5) is the other form of equation (1).
in Fig.1-b) and w is the height of side weir.Combination of equations (1) and (2) yields the equation (4). Moreover, it is evident that equation (5) is the other form of equation (1). 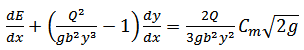
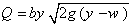
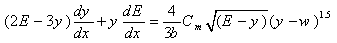
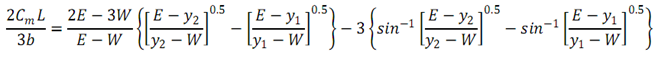

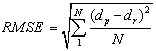
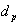 stands for predicted value and
stands for predicted value and 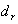 is representative of observed values and N is the number of data. The volume of results is beyond this paper, this methodology was implemented for all the subdivision conditions defined previously and the best results are reported in table (3). The table represents the best equation for any condition (Froude number, the ratio of side weir length to main channel width and the depth of water to the height of side weir).
is representative of observed values and N is the number of data. The volume of results is beyond this paper, this methodology was implemented for all the subdivision conditions defined previously and the best results are reported in table (3). The table represents the best equation for any condition (Froude number, the ratio of side weir length to main channel width and the depth of water to the height of side weir).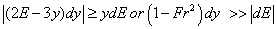




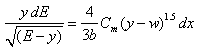
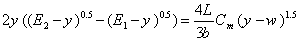

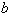 : Width of main channel
: Width of main channel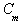 : Discharge coefficient
: Discharge coefficient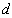 : Data used for statistical operations
: Data used for statistical operations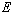 : Specific energy of water
: Specific energy of water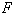 : Unknown function
: Unknown function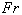 : Froude number (=
: Froude number (=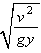 )
)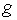 : Gravitational acceleration (m/s²)
: Gravitational acceleration (m/s²)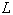 : Length of the side weir
: Length of the side weir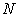 : Number of data used in statistical operations
: Number of data used in statistical operations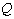 : Discharge of water
: Discharge of water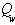 : discharge passing weir
: discharge passing weir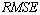 : Root Mean Square Error (equation 8)
: Root Mean Square Error (equation 8)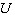 : Velocity in main direction
: Velocity in main direction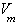 : Total Velocity
: Total Velocity 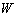 : Height of side weir
: Height of side weir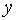 : Depth of water
: Depth of water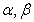 : Constants used in discharge coefficient equations
: Constants used in discharge coefficient equations  Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML

