| [1] | Barr, D. I. H. (1977). "Discussion on "Accurate explicit equations for friction factor," by A.K.Jain." J. Hydraul. Div. Am. Soc. Civ. Eng., 103(3), 334-337. |
| [2] | Bombardelli, F., and Garcia, M. (2003). "Hydraulic Design of Large-Diameter Pipes." J.Hydraul.Eng., 129(11), 839-846. |
| [3] | Brkić, D. (2011a). "New explicit correlations for turbulent flow friction factor." Nucl.Eng.Des., 241(9), 4055-4059. |
| [4] | Brkić, D. (2011b). “Review of explicit approximations to the Colebrook relation for flow friction.” Journal of Petroleum Science and Engineering, Vol. 77, Issue 1, April 2011, 34–48. |
| [5] | Clamond, D. (2009). "Efficient Resolution of the Colebrook Equation." Ind Eng Chem Res, 48(7), 3665-3671. |
| [6] | Colebrook, C. F. (1939). "Turbulent flow in Pipes, with particular reference to the transition region between the smooth and rough pipe laws." J. Inst. Civil Eng., 11(4), 133-156. |
| [7] | Danish, M., Kumar, S., and Kumar, S. (2011). "Approximate explicit analytical expressions of friction factor for flow of Bingham fluids in smooth pipes using Adomian decomposition method." Communications in Nonlinear Science and Numerical Simulation, 16(1), 239-251. |
| [8] | Diniz, V. E. M. G., and Souza, P. A. (2009). "Four explicit formulae for friction factor calculation in pipe flow." Transactions on Ecology and the Wnvironment, 125 369-380. |
| [9] | Fang, X., Xu, Y., and Zhou, Z. (2011). "New correlations of single-phase friction factor for turbulent pipe flow and evaluation of existing single-phase friction factor correlations." Nucl.Eng.Des., 241(3), 897-902. |
| [10] | Giustolisi, O., L. Berardi, L., and Walski, T. M. (2011). "Some explicit formulations of Colebrook–White frictionfactor considering accuracy vs. computational speed." Journal of Hydroinformatics, 13(3), 401-418. |
| [11] | Gulyani, B. B. (2001). "Approximating equations for pipe sizing." Chemical Engineering, 108(2), 105-108. |
| [12] | Haaland, S. E. (1983). "Simple and Explicit Formulas for the Friction Factor in Turbulent Pipe Flow." J.Fluids Eng., 105(1), 89-90. |
| [13] | Imbrahim, C. (2005). "Simplified equations calculates head losses in comercial pipes." The Journal of American Science, 1(1), 1-2. |
| [14] | Jain, K. (1976). "Accurate explicit equation for friction factor." Journal of Hydraulics Division, ASCE, 102(HY5), 674-677. |
| [15] | Li, P., Seem, J. E., and Li, Y. (2011). "A new explicit equation for accurate friction factor calculation of smooth pipes." Int.J.Refrig., 34(6), 1535-1541. |
| [16] | Moody, L. F. (1947). "An approximate formula for pipe friction factors." Mech. Engng., 69 1005-1006. |
| [17] | Nikuradse, J. (1933). "Stroemungsgesetze in rauhen Rohren." Ver. Dtsch. Ing. Forsch., 361 1-22. |
| [18] | Prandtl, I. (1952). Essentials of fluid dynamics ,Hafner,New York. |
| [19] | Romeo, E., Royo, C., and Monzón, A. (2002). "Improved explicit equations for estimation of the friction factor in rough and smooth pipes." Chem.Eng.J., 86(3), 369-374. |
| [20] | Sonnad, J., and Goudar, C. (2006). "Turbulent Flow Friction Factor Calculation Using a Mathematically Exact Alternative to the Colebrook–White Equation." J.Hydraul.Eng., 132(8), 863-867. |
| [21] | Swamee, P. K., and Jain, A. K. (1976). "Explicit equations for pipe flow problems." J.Hydraul.Eng. ASCE, 102(5), 657-664. |
| [22] | Swamee, P. K., and Rathie, P. N. (2007). "Exact equations for pipe-flow problems" Journal of Hydraulic Research, 45(1), 131-134. |
| [23] | Swamee, P. K., and Swamee, N. (2007). "Full-range pipe-flow equations." Journal of Hydraulic Research, 45(6), 841-843. |
| [24] | Valiantzas, J. (2008). "Explicit Power Formula for the Darcy–Weisbach Pipe Flow Equation: Application in Optimal Pipeline Design." J.Irrig. Drain. Eng., 134(4), 454-461. |
| [25] | von Karman, T. (1934). "The fundamentals of the statistical theory of turbulence." J. Aero Sci., 4 131-138. |
| [26] | Yıldırım, G. (2009). "Computer-based analysis of explicit approximations to the implicit Colebrook–White equation in turbulent flow friction factor calculation." Advances in Engineering Software (1992), 40(11), 1183-1190. |
| [27] | Yildirim, G. (2010). "A MathCAD procedure for commercial pipeline hydraulic design considering local energy losses." Advances in Engineering Software (1978), 41(3), 489. |

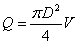
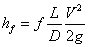
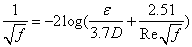
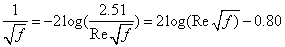
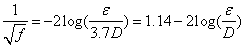
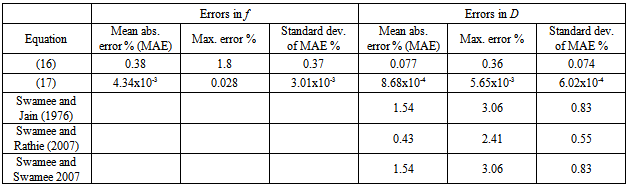
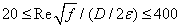 can be represented by a continuous curve which is asymptotic to Eqs. (4) and (5). With this important observation Colebrook derived Eq. (3) by using Eqs. (4) and (5) without explanation of the additive property of the terms in the logarithm. The Colebrook-White equation (3) is implicit in f requiring a numerical iterative procedure for its solution. This complexity does not affect the problem of type I (computation of discharge, Q) because Q can be computed by a closed-form equation: By computing
can be represented by a continuous curve which is asymptotic to Eqs. (4) and (5). With this important observation Colebrook derived Eq. (3) by using Eqs. (4) and (5) without explanation of the additive property of the terms in the logarithm. The Colebrook-White equation (3) is implicit in f requiring a numerical iterative procedure for its solution. This complexity does not affect the problem of type I (computation of discharge, Q) because Q can be computed by a closed-form equation: By computing 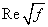 where the velocity V is estimated by Eq. (2), substituting in the right hand side of Eq. (3), and computing Q from Darcy – Weisbach equation, the following equation is derived for Q:
where the velocity V is estimated by Eq. (2), substituting in the right hand side of Eq. (3), and computing Q from Darcy – Weisbach equation, the following equation is derived for Q: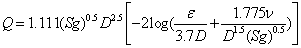
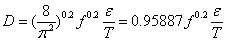
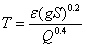
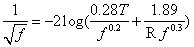
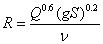
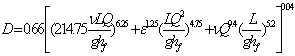
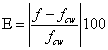
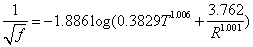
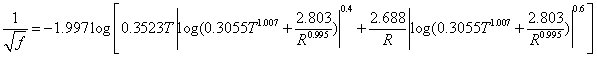
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML