-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Hydraulic Engineering
2012; 1(5): 43-47
doi: 10.5923/j.ijhe.20120105.03
Evaluation of Synthetic Unit Hydrograph (SCS) and Rational Methods in Peak Flow Estimation (Case Study: Khoshehaye Zarrin Watershed, Iran)
A. Majidi 1, M. Moradi 1, H. Vagharfard 2, A. purjenaie 1
1Graduate Watershed management, Natural Resources Faculty, Hormozgan University, Iran
2Natural Resources Faculty, Hormozgan Agricultural Sciences & Natural Resources University, Iran
Correspondence to: A. Majidi , Graduate Watershed management, Natural Resources Faculty, Hormozgan University, Iran.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
The leakage of statistic and data of hydrometry gages is the one of basic difficulties in peak flow estimation with different return periods, because of this estimation of peak flow in these gages are more importance. Khoshehaye Zarrin watershed did not have any hydrometry gages So, the present research is conducted with goal of determining amount of peak flow with two methods that mentioned in the title, firstly we calculated the run-off coefficient and rainfall intensity in each sub basin with Rational method, then with calculating of run-off height by curve number, peak flow was calculated for each sub basin and according to this, the dimensionless unit hydrograph was drawn. For assessment of accuracy of these two methods, we compared their results with nearest gage. The results showed that SCS method has accurate estimation than Rational method and it can be used for peak flow estimation in the similar condition watersheds.
Keywords: Peak Flow, Synthetic Unit Hydrograph, Rational, Khoshehaye Zarrin Watershed, Iran
Cite this paper: A. Majidi , M. Moradi , H. Vagharfard , A. purjenaie , "Evaluation of Synthetic Unit Hydrograph (SCS) and Rational Methods in Peak Flow Estimation (Case Study: Khoshehaye Zarrin Watershed, Iran)", International Journal of Hydraulic Engineering, Vol. 1 No. 5, 2012, pp. 43-47. doi: 10.5923/j.ijhe.20120105.03.
Article Outline
1. Introduction
- Nowadays peak flow estimation from storms in small basins and no-statistics especially is very important for hydrologists[4]. Peak estimation from precipitation is always one of the basic problems of the watershed and it causes that many of implemented projects are encountered with numerous problems[2,9]. Therefore using of peak flow estimation methods is very important in no-gage watersheds and selection of the most accurate estimation seems necessary with use of available statistics[16]. Several researches have conducted about evaluation of peak flow estimation methods[10,12,14,17,1]. Shahmohammadi studied peak flow estimation with use of SCS, Triangular dimensional and Snyder’s unit hydrographs methods in Khorasan watershed, Iran. The results showed that SCS unit hydrograph method estimated peak flows with less error than the others methods[19]. Barkhordai et al studied Clark, SCS, Triangular dimensional and Snyder’s unit hydrographs methods evaluation in peak flow estimation in Sikhoran watershed, Iran. Their results showed that for selecting unit hydrograph method in no-statistics watersheds, SCS and Triangular dimensional methods for low-slope watersheds and Clark and Snyder’s mountainous watersheds show the best estimation[3]. methods for Cheng; Cheng et al and Taguas et al have used Rational method in peak flow estimation in small watersheds and they have determined direct run-off coefficient between 0.8-1 and also their resulted showed that there are not difference between observation and estimated discharges[5,6,20]. Considering Khoshehaye Zarrin watershed has no hydrometry gage and peak flow measurements have not done, therefore we have used valid and acceptable empirical methods for peak flow estimation in this research.
2. Data and Methodology
2.1. Study Area
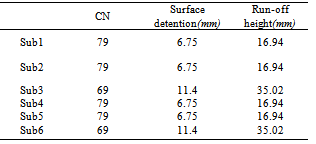
- Khoshehaye Zarrin watershed is located in Arak province, Iran, between 50° 08' 52" to 50° 15' 42.85" E and 35° 37' 33.4" to 35° 54' 30" N. Its area is 8362 hectares and it has been divided to 6 hydrological units based on drainage pattern. Its maximum elevation is 1380 m and its minimum elevation is 1100 m in the watershed outlet. The mean annual rainfall is 197.5 mm and its general slope is northwest to southeast. Khoshehaye Zarrin watershed has two permanent rivers that these rivers are the most important source of irrigation of Khoshehaye Zarrin region. Figure (1) shows Khoshehaye Zarrin watershed location and table (1) shows some physiographic characteristics of its sub-basins.
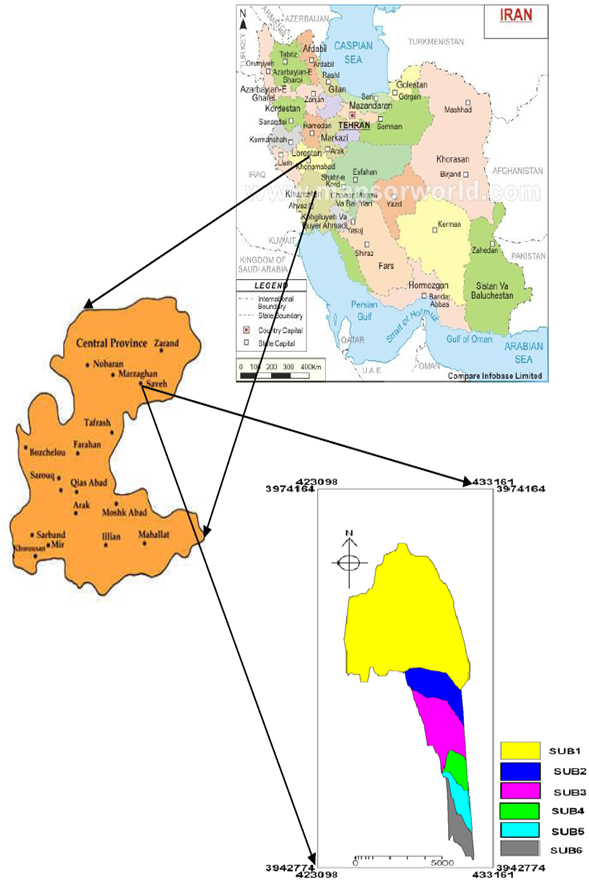 | Figure 1. Khoshehaye Zarrin watershed location |
2.2. Study Method
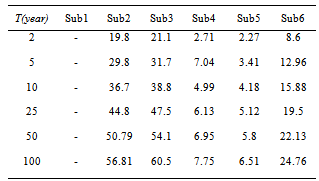
- We have used rainfall data and field studies for analysing in Khoshehaye Zarrin watershed. Then following empirical methods used for estimating of flood discharges in the study area due to high relative accuracy:
2.2.1. Rational Method
- This method uses for small watersheds (about 1000 till 5000 hectares) and therein is assumed that rainfall falls with constant intensity and uniform in all basins. The major defect of this method is ignoring the factors such as soil moisture and temperature but ease of its use caused to be used widely[13]. This method is given by following equation (1).
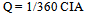 | (1) |
2.2.2. SCS Unit Hydrograph Method
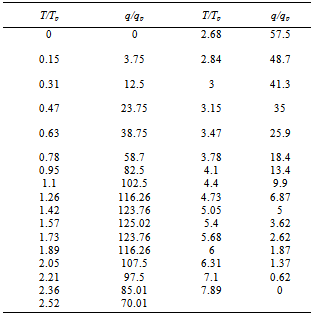
- A unit hydrograph is expressed as direct run-off due to one inch of rainfall excess and its figure is characteristic function of basin[7]. Unit hydrograph can be used synthetically and using physical factors of Basin in cases there is no hydrometry gage. Mockus (1957) showed a dimensionless unit hydrograph with the study of accomplished measurement by USA Soil Conservation Service that it has T/Tp and q/qp axis. For determining of synthetic unit hydrograph in this method, time to peak (Tp) and peak flow (qp) must be calculated. Equations (2) and (3) are used for determining (Tp) and (qp)[13].
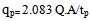 | (2) |
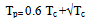 | (3) |
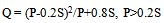 | (4) |
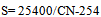 | (5) |
3. Results and Discussion
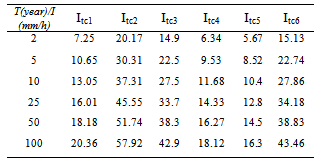
- With regard to no record of rain recorder data with appropriate statistical period in Khoshehaye Zarrin watershed, rainfall intensity in time of concentration with different return periods estimated by Ghahraman and Abkhezr’s equation[8]. Rainfall intensity in time of concentration in study watershed is shown in table (2).
|
|
|
|
|
|
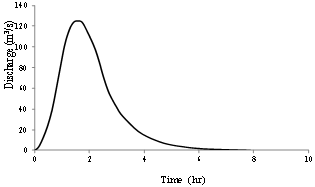 | Figure 2. Dimensionless unit hydrograph for sub-basin 1 |
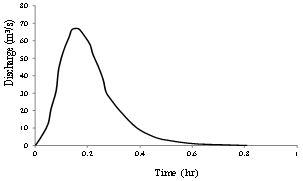 | Figure 3. Dimensionless unit hydrograph for sub-basin 4 |
4. Conclusions
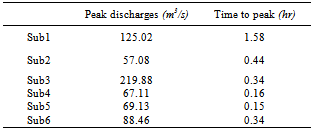
- With regard to this point that Khoshehaye Zarrin watershed has no hydrometry gage and peak flow measurements have not done, so we used the nearest data of hydrometry gage to study watershed for evaluating accuracy. This research results showed that Synthetic Unit Hydrograph (SCS) method has more accurate estimate than Rational method and also this method estimated watershed flood hydrographs with less error than Rational method and so it can be used for peak flow estimation in the similar condition watersheds. This research results correspond with results of studies such as Khosroshahi[11] and Musavi[15]. Meanwhile, the study watershed has intense rains and high flooding so that sub-basin 3 with 220 (m3/s) is the most flooding and versus sub-basin 2 with 57 (m3/s) is the least flooding that their reason is hydrological and physiographic conditions of sub-basins 3 and 2 and we suggest that sub-basin 3 should be considered in first priority of flood control.
ACKNOWLEDGMENTS
- The authors greatly acknowledge the financial supports of Khoshehaye Zarrin (of all organic pomegranate crops), provided for running the present project.
References
| [1] | Abdi, M. Fathzade, A. and Palizdan, N., 2009, Determination of the best method of annual run-off estimation in no-statistic watersheds (Case study: Sunich watershed, Iran), 2th National drought effects conference, Esfahan, 1-7. |
| [2] | Akhondi, A., 2001, Checking curve number model in flood estimation by GIS, M.Sc. thesis in agriculture and natural resources , Tarbiat Moddares university, p94. |
| [3] | Barkhordai, J. Telvari, A. Ghyasi, N. and Rastgar, H., 2006, Checking and evaluating synthetic unit hydrograph methods in flood estimation in Sikhoran watershed, Research and construction journal in natural resources, 71, 57-65. |
| [4] | Behbahani, S. M. R., 2002, Surface water hydrology, Tehran university press. p488. |
| [5] | Cheng, J. D., 1997, Small watershed peak flow estimation, Joyrnal of Soil and Water Conversation, 29, 3, 306-315. |
| [6] | Cheng, Q. Li, L. and Wang, L., 2009, Characterization of peak flow events with local singularity method, Nonlin, Processes Geophys, 16, 503–513. |
| [7] | Curtis Weaver, J., 2003, Methods for Estimating Peak Discharges and Unit Hydrographs for Streams in the City of Charlotte and Mecklenburg County, North Carolina. Water-Resources Investigations Report 03–4108, p55. |
| [8] | Ghahraman, B. and Abkhezr, H. R., 2004, Improvement in Intensity-Duration-Frequency Relationships of Rainfall in Iran, agriculture and natural resources journal, 8, 2, 1-13. |
| [9] | Gholami, A. Mahdavi, M. Ghanadha, M. and Vafakhah, M., 2001, An evaluation of suitable probability distributions for minimum, mean and maximum discharges, using L moment method (Case study: Mazandaran province), Iranian journal of natural resources, 54, 4, 345-354. |
| [10] | Khosla, A. N., 1949, Analysis and utilization of data for the appraisal of water resources, Journal of Irrigation Power. India, 410-422. |
| [11] | Khosroshahi, F., 1991, Evaluation of unit hydrograph in flood estimation, 1th Iran hydrology conference, 1-18. |
| [12] | Kothyari, U. C., 1995, Estimation of monthly runoff from small catchments in India. Hydrological Sciences, 40, 4, 533-543. |
| [13] | Mahdavi, M., 2009, Applied hydrology, Vol. 2, Tehran university press, p437. |
| [14] | Mohammadpoor, M. Akhondali, A. M. and Nasajizavare, M., 2007, Discharge estimation in no-statistic watersheds (Case study: Ala and Roodzard rivers), 9th National Irrigation conference, Kerman, 1-8. |
| [15] | Musavi, F., 1998, Study and Test of Fitting Natural and Synthetic Unit Hydrographs in Zayandehrud-dam Watershed (Pelasjan Sub-basin), Agriculture and natural resources journal, 2, 2, 93-107. |
| [16] | Movaheddanesh, A. A., 1994, History of hydrology, Vol. 3, Amidi press, p54. |
| [17] | Patil, J. P. Sarangi, A. Singh, A. K. and Ahmad, T., 2008, Evaluation of modified CN methods for watershed runoff estimation using a GIS-based interface, Biosystems Engineering, 100, 1, 137-146. |
| [18] | Razavi, S. L. Sadeghi, S. H. R. and Mahdavi, M., 2010, Increase of SCS model estimation accuracy by precipitation replacement with precipitation in time of concentration of khanmirza and kesilian watersheds, 6th National watershed and 4th national erosion and sediment conferences, 1-8. |
| [19] | Shahmohammadi, Z., 1994, Evaluation of synthetic unit hydrograph methods in Khorasan watershed, M.Sc. thesis, Tehran University. |
| [20] | Taguas, E. V. Ayuso, J. L. Pena, A. Yuan, Y. Sanchez, M. C. Giraldez, J. V. and Pérez, R., 2008, Testing the relationship between instantaneous peak flow and mean daily flow in a Mediterranean Area Southeast Spain. Catena, 75, 2, 129-137 |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML