Avinash M. Badar, Aniruddha D. Ghare
Dept. of Civil Engineering, Visvesvaraya National Institute of Technology, Nagpur, 440010, India
Correspondence to: Aniruddha D. Ghare, Dept. of Civil Engineering, Visvesvaraya National Institute of Technology, Nagpur, 440010, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
Consumption of water can be optimized by metering it. In irrigation systems, many lined irrigation canals have trapezoidal cross sections. A simple portable device for measurement of discharge in small trapezoidal agricultural canal has been analyzed in this paper. Measuring flume consists of a cylinder positioned axially in nearly horizontal prismatic trapezoidal channel which can be quickly fixed and removed for short-time use in trapezoidal channels. The cylinder placed in the flow reduces the cross section for flow, thus creating critical flow conditions. In this paper, a new mathematical model has been developed to predict the discharge through a trapezoidal canal by simple cylindrical flume using experimental data available in literature for trapezoidal canal having 1:1 side slope. Dimensional analysis has been carried out to achieve the objective of prediction of more accurate discharge than that calculated by a model available in the literature. The resulting non-dimensional parameters have been used to develop the proposed mathematical model and the results of the proposed model have been compared with the results of the model available in the literature.
Keywords:
Flume, Discharge Measurement, Open Channel Flow, Dimensional Analysis
Cite this paper: Avinash M. Badar, Aniruddha D. Ghare, Development of Discharge Prediction Model for Trapezoidal Canals using Simple Portable Flume, International Journal of Hydraulic Engineering, Vol. 1 No. 5, 2012, pp. 37-42. doi: 10.5923/j.ijhe.20120105.02.
1. Introduction
Water is vitally important natural resource for mankind and is a valuable national asset. Efficient development and optimum utilization of water resources is of great significance to the overall development of the country. Accurate measurement of irrigation water results in more intelligent use of this valuable natural resource. Such measurement reduces excessive waste and allows the water to be distributed among users according to their needs and the importance.Various approaches exist to measure discharge in canals. The usual discharge measurement in canals is based on the critical flow concept. Most of previous works for discharge measurement structures were carried out in canals with rectangular cross sections. However, in irrigation systems, specially the lined canals, have trapezoidal cross sections.Hence an attempt is made to develop a refined mathematical model for prediction of discharge through trapezoidal canal having 1:1 side slope, using experimental data on simple cylindrical flume presented by Samani et al.[1].There are two strategies for discharge measurements in canals. A structure can be mounted permanently or it can be temporarily positioned in the canal for discharge evaluation. The critical flow condition can be attained for constant discharge and steady flow conditions. This can be achieved either by local contractions or by local bottom elevations or by both. For recording discharge at different points in irrigation canal system over a limited period, a mobile apparatus would be convenient. Such apparatus should be light in weight and easily adjustable in the channel. This advantage is offered by the simple cylindrical portable flume. The literature shows the use of various flumes, most of which are of fixed type. Parshall flumes are characterized by cross-section with various degrees of convergence and divergence. Skogerboe[2] developed the cutthroat flume, which has only two sections, viz., converging section and diverging section and has no throat. Replogle[3] presented Replogle – Bos Clemers (RBC) flumes which posed sedimentation problems at its entrance. Hager[4] determined discharge-head relations for trapezoidal canals by using models that accounted for the streamline slope and curvature. Hager[5] measured the discharge in circular channel by inserting a circular conduit. Samani et al.[1] based on the parameters measured in the laboratory, developed a computer model for calibration of simple cylindrical portable flume. The flume consisted of a pipe installed axially inside a trapezoidal canal with the side slope 1:1, as shown in Figure 1. Samani et al.[6] also proposed another simple flume consisting of two semi-cylinders attached to each of the side walls of the rectangular channel. Baiamonte, et al.[7] presented a flume for measuring flow discharge in sloping rectangular channels using two half cylinders and determined the two coefficients of the power stage-discharge equation.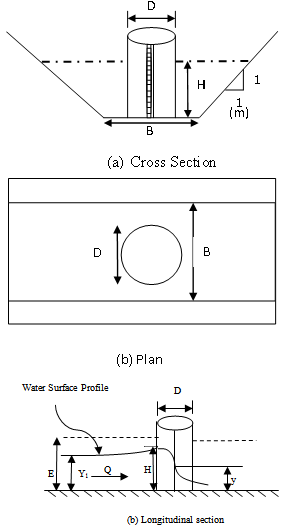 | Figure 1. Simple Cylindrical Flume |
2. Theoretical Analysis of Flow through Simple Cylindrical Flume
Discharge measurement in open channels is based on the principle of critical flow. Specific energy on upstream of critical section assuming uniform velocity distribution can be expressed as; | (1) |
By considering a horizontal contracted flume, and neglecting the energy loss between upstream and critical flow section, the upstream energy and the energy at critical section can be obtained by | (2) |
The critical flow occurs between cylindrical column and canal where water reaches the smallest cross section for the canal. At critical section Froude Number is unity. The critical flow equation can be described as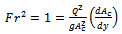 | (3) |
in which  represents the derivative of critical flow cross section with respect to flow depth.From Equation (2) and Equation (3),
represents the derivative of critical flow cross section with respect to flow depth.From Equation (2) and Equation (3), | (4) |
If vertical pipe of diameter ‘D’ is placed centrally in a trapezoidal canal, then cross section at the critical point Ac as function of Y can be expressed as  | (5) |
Equations (3) and (4) can be used for determination of Q and Y, if the upstream energy is measured.
3. Dimensional Analysis for Simple Cylindrical Flume
Dimensional analysis is used to obtain a functional relationship between the variables in terms of non-dimensional parameters, which are used to form the best fit equation describing the phenomenon. Buckingham’s Π method of dimensional analysis has been used for development of the discharge relationship.The relationship between the upstream energy head ‘H’& the discharge ‘Q’ for a trapezoidal flume having horizontal bottom, formed by contracting the flow by placing a cylinder of diameter ‘D’ centrally at the canal bottom with width ‘B’, can be expressed as - | (6) |
Total number of variables is 5. There are only two fundamental dimensions involved i.e. L & T. Therefore, there are 3 dimensionless Π terms.According to the Π theorem of dimensional analysis, the functional relationship given by Equation (6) can be expressed by using only three dimensionless groups. 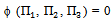 | (7) |
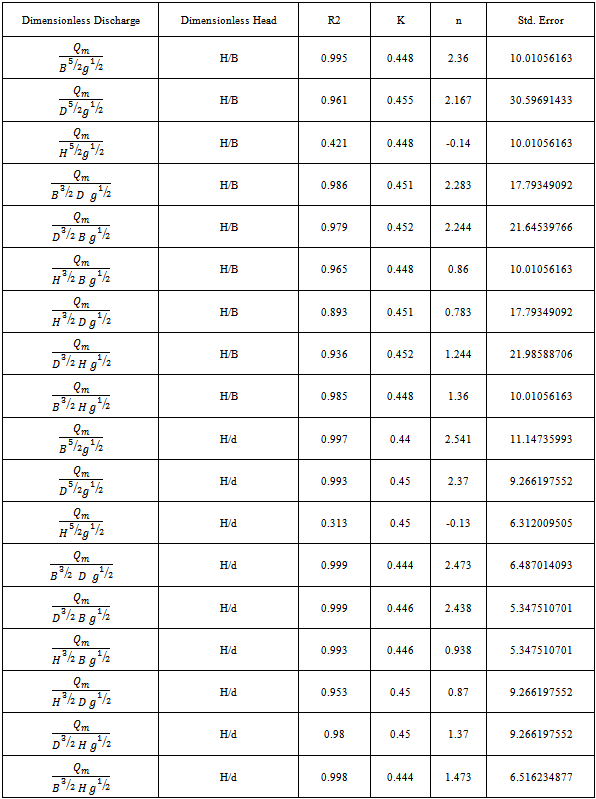
where Π1, Π2 & Π3 are dimensionless groups whose expressions have to be determined. Let B and g be the repeating variables.Π terms have been grouped as follows : | (8) |
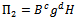 | (9) |
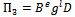 | (10) |
Where a, b, c, d, e and l are numerical constants.Substituting the measurement units of each variable in Equations (8), (9) and (10),  | (11) |
 | (12) |
Table 1. Results of Regression Analysis
 |
| |
|
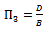 | (13) |
Substituting Equations (11), (12), (13) into Equation (7), 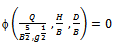 | (14) |
Similarly, from the permutations and combinations, following equations can be obtained 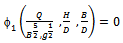 | (15) |
 | (16) |
The different combinations of dimensionless discharges and head terms for simple cylindrical portable flume in trapezoidal canal have been generated and are listed in Table 1.
4. Regression Analysis
A discharge model can be developed using the observed column head readings. The dimensionless discharge can be expressed as the exponential function of dimensionless head. The regression analysis has been carried out for the best fit correlation between dimensionless discharge and dimensionless head for establishment of dimensionless relationship for the data given by Samani et al.[1]. Nine combinations of dimensionless discharge and two combinations of dimensionless head have been considered. A total of eighteen combinations have been considered for assessing the variation of dimensionless discharge with dimensionless head. Regression analysis has been carried out as shown in Table 1. Power model for fitness of trend line, in the form y = k . xn was found to be appropriate to yield high value of R2. Figure 2 shows the variation of (Qm/(D3/2*B*g1/2)) with H/D using measured flow rates (Samani et al.[1]). 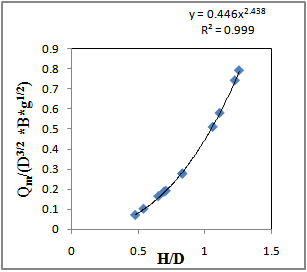 | Figure 2. Plot of Variation of (Qm/(D3/2 *B*g1/2)) with H/D |
Correlation coefficient (R2) is a measure of well predicted values from a set of observed values. Numerically it cannot exceed unity. It always lies between 0 and 1. Correlation between the variables of equation, (Qm/(D3/2*B*g1/2)) and H/D, gave the value of coefficient of determination, R2 = 0.999. This regression coefficient suggests that the model is very good and hence can be adopted. The developed mathematical model is given by  | (17) |
5. Comparison of Proposed Mathematical Model with Samani’s Model
Proposed model (Eq 17) incorporates all the governing parameters affecting the flow rate such as base width, diameter of the cylinder, upstream energy, whereas the model developed by Samani et al.[1] incorporated canal base width and the upstream energy and was given by Equation (18).  | (18) |
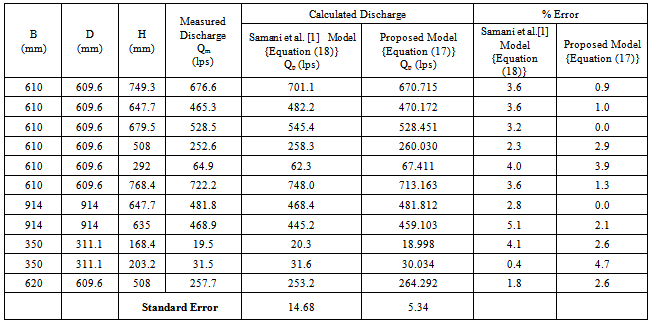
The discharge is calculated for comparing the accuracy of the developed model, i.e. Equation (17); with the model obtained by Samani et al.[1], i.e. Equation (18). This comparison is shown in Figure 3.The mean percentage error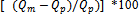 between measured discharge and predicted discharge has been calculated and shown in Table 2. It is found that the % error lie within ± 4.7% when proposed model {Equation (17)} is used, whereas, in case of Samani et al.[1] model {Equation (18)}, the % error is found to be ± 5.1%.The standard error is a measure of accuracy of predictions. The size of the standard error also helps up to assess the quality of regression model. The standard error has been calculated by –
between measured discharge and predicted discharge has been calculated and shown in Table 2. It is found that the % error lie within ± 4.7% when proposed model {Equation (17)} is used, whereas, in case of Samani et al.[1] model {Equation (18)}, the % error is found to be ± 5.1%.The standard error is a measure of accuracy of predictions. The size of the standard error also helps up to assess the quality of regression model. The standard error has been calculated by – Standard error as per Samani et al.[1] model is found to be 14.68 whereas as per the proposed model, it is found to be 5.34. These results are shown in Table 3. Thus, it is evident from the comparison that the developed mathematical model {Equation (17)}, gives more accurate predicted discharge for a simple cylindrical portable flume.
Standard error as per Samani et al.[1] model is found to be 14.68 whereas as per the proposed model, it is found to be 5.34. These results are shown in Table 3. Thus, it is evident from the comparison that the developed mathematical model {Equation (17)}, gives more accurate predicted discharge for a simple cylindrical portable flume. | Figure 3. Comparison of measured discharge with proposed model {Equation (17)} |
Table 2. Comparison of Measured Discharge with Calculated Discharge
 |
| |
|
| Table 3. Comparison of Samani et al. model[1] with the Proposed model |
| | Factor | Samani’s Model,Equation (18) | Proposed Model, Equation (17) | | Mean % error | ± 5.1 | ± 4.7 | | Standard error | 14.68 | 5.34 |
|
|
6. Conclusions
Simple cylindrical portable flume can be used as a mobile discharge measurement device for small sized trapezoidal canals on irrigation fields. The discharge can be estimated using the proposed mathematical model {Equation (17)}, which incorporates the channel bed width, diameter of cylinder and the column head reading. Proposed model incorporates all the influencing parameters governing the flow as compared to the Samani et al.[1] model{Equation (18)}, which used only bottom width and the column head reading. The actual measured flow rates have been compared with the calculated flow rates by both the models i.e. Samani et. al.[1] model {Equation (18)} and the proposed model {Equation (17)}. The results of the comparison show that the proposed mathematical model {Equation (17)} predicts more accurate discharge with maximum error upto 4.7% as compared to Samani et al.[1] model{Equation (18)}, which has maximum error upto 5.1%. Also the standard error, in case of proposed model is found to be 5.34 as compared to Samani et al.[1] model{Equation (18)}, which is found to be 14.68. The proposed mathematical model is valid for only the trapezoidal section with side slopes of 1:1. There is need to collect more experimental data for different side slopes (m:1), so that a more generalized mathematical model can be developed.
NOTATIONS
The following symbols are used in this paper:a, b, c, d, e, l - Numerical constant;A - Cross sectional area of flow;AC -Cross sectional area of flow at critical flow section;B - Canal bottom width;D - Diameter of column pipe;E - Upstream energy;EC - Energy at the critical flow section;f - Function;Fr - Froude number;g - Acceleration due to gravity;H - Column reading;K - Coefficient in head-discharge relation;m - Side slope;n - Exponent in head-discharge relation;N - Number of observations;Q - Flow rate;Qm - Measured Discharge;Qp - Predicted Discharge by proposed model;Qps - Predicted Discharge by Samani Model;r - Qp/Qm = Discrepancy ratio;R2 - Coefficient of determination;Y - distance from the surface of water at the critical point to the flume floor;Y1 - depth of water at upstream of critical section;Φ - Function;y - Y – axis parameter;x - X – axis parameter.
References
| [1] | Samani, Z., and Magallanez, H. (1993). ‘‘Measuring water in trapezoidal Canals,’’ Journal of Irrigation and Drainage Engineering, ASCE, Vol –119, No -1,Pg.-181–186. |
| [2] | Skogerboe, G. V., and Hyatt, M.L., (1967), “Rectangular cut throat flumes”, Journal of Irrigation and Drainage Engineering Div., 98(4), 569-583. |
| [3] | Replogle, J.A. (1975) “Critical flow flumes with complex cross sections.” Proc., Irrig. Drain. Div. Spec. Conf., ASCE, New York, N.Y., 336-338. |
| [4] | Hager, W. H. (1985). “Modified Venturi Channel,” Journal of Irrigation and Drainage Engineering., ASCE, Vol– 111, No - 1, Pg. - 19-35 |
| [5] | Hager, W. H. (1988).“Mobile Flume for Circular Channel,” Journal of Irrigation and Drainage Engineering., ASCE, Vol – 114, No - 3, Pg. - 558-566. |
| [6] | Samani, Z., and Magallanez, H. (2000).“Simple flume for flow measurement in open channel.”Journal of Irrigation and Drainage Engineering, ASCE, Vol – 126, No. 2, Pg. No.127–129. |
| [7] | Baiamonte, G., and Ferro, V., (2007). “Simple flume for measurement in sloping open channel”, Journal of Irrigation and Drainage Engineering, ASCE, V01-113, No.-1, Pg -71-78 |




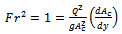
 represents the derivative of critical flow cross section with respect to flow depth.From Equation (2) and Equation (3),
represents the derivative of critical flow cross section with respect to flow depth.From Equation (2) and Equation (3),


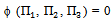

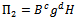
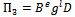


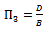
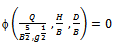
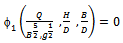




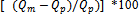 between measured discharge and predicted discharge has been calculated and shown in Table 2. It is found that the % error lie within ± 4.7% when proposed model {Equation (17)} is used, whereas, in case of Samani et al.[1] model {Equation (18)}, the % error is found to be ± 5.1%.The standard error is a measure of accuracy of predictions. The size of the standard error also helps up to assess the quality of regression model. The standard error has been calculated by –
between measured discharge and predicted discharge has been calculated and shown in Table 2. It is found that the % error lie within ± 4.7% when proposed model {Equation (17)} is used, whereas, in case of Samani et al.[1] model {Equation (18)}, the % error is found to be ± 5.1%.The standard error is a measure of accuracy of predictions. The size of the standard error also helps up to assess the quality of regression model. The standard error has been calculated by – Standard error as per Samani et al.[1] model is found to be 14.68 whereas as per the proposed model, it is found to be 5.34. These results are shown in Table 3. Thus, it is evident from the comparison that the developed mathematical model {Equation (17)}, gives more accurate predicted discharge for a simple cylindrical portable flume.
Standard error as per Samani et al.[1] model is found to be 14.68 whereas as per the proposed model, it is found to be 5.34. These results are shown in Table 3. Thus, it is evident from the comparison that the developed mathematical model {Equation (17)}, gives more accurate predicted discharge for a simple cylindrical portable flume.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML
