Edward Ching-Ruey LUO
Department of Civil Engineering, National Chi-Nan University, Nanto County, 545, Taiwan
Correspondence to: Edward Ching-Ruey LUO, Department of Civil Engineering, National Chi-Nan University, Nanto County, 545, Taiwan.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
Generally, the natural rivers or sometimes the artificial channels are composed of a deep main channel with one or two shallow flood plains. The flow situation must be a 3D condition, while on purpose of hydraulic management, it is necessary treated as 1D to calculate the corresponding hydraulic characteristics. And the energy and momentum coefficients to correct the effect of non-uniformity of velocity distribution are needed to adopt. In this paper, the straight symmetric compound-channel flow is researched beginning with dimensional analysis to find the variables affecting these two coefficients. The main factors, such as the reciprocal of Reynold’s number and cross-section shape including water depth and main channel width, influencing the phenomena of the two coefficients in main channel, flood plain and total section are analysed and discussed.
Keywords:
Compound Channel Flow, Energy Coefficient, Momentum Coefficient, Regression, Velocity Distribution
1. Introduction
In general, natural rivers or artificial channels are composed of a deep main channel and one or two shallow flood plains near the main channel. The compound channel flow is very complicated, and it is a three-dimensional flow condition. While engaging in river management, we often treat nature river flow as one-dimensional flow condition to calculate its hydraulic characteristics. It needs to adopt the energy coefficient and the momentum coefficient to correct the effect of the non-uniformity of velocity distribution. The dimensional analysis method is used to find the variables that affect energy coefficient and momentum coefficient in straight compound open channel flow, and the hydraulic flume test was carried out to investigate the relationship of the energy coefficient and momentum coefficient in straight compound channel with the change of relevant variables from dimensional analysis, such as Reynold’s number, cross-section shape, or relative water depth for main channel, flood plain and total section. We also discuss the limitation of Reynold’s number in this paper.
2. Similarity and Experiment Results
The dimensional analysis of similarity on straight symmetric compound-channel flow was shown in many papers, such as Knight and Demetriou[1], Knight and Hamed[2], Wormleaton et.al[3],Wormleaton and Hadjipanos[4], Prinos et.al[5], Myers[6], and Myers and Brennan[7]. The equations of continuity, momentum and energy for one-dimension open channel flow of Field et.al[8] were used. Some powerful experimental data are used to directly calculate and regress the equations for the energy and momentum coefficients, and the results and comparisons are presented here.The obvious mechanisms and factors for set-up of the experiment are b/B=0.214, 0.257, 0.314, 0.371, and 0.414; d/D=0.375, 0.348, 0.286, 0.250, and 0.211; b/h =1, 1.2, 1.467, 1.733, and 1.933; b=0.22m, 0.26m, and 0.29m; b/D=from 0.917 to1.381; bf /2d =from 2.28 to 4.00; So=0.001 and Qt =from 4.95 l/s to 27.6 l/s. Totally 53 sets of data are generated. The positions for the above mentioned situations are expressed in figure 1. The definition will be given in the following section.
2.1. Figures and Tables
Please see the figure 1, for presenting the set-up of experiment figure in the calculation from the experimental real data. The results of regressions, as follows, are from Table 1 to Table 3.
2.2. Abbreviations and Acronyms
The Definitions of each abbreviation and acronym are:B (m), the width of water surface; b (m), the width of main channel; bf (m), the width of symmetric flood plain=B-b; h (m), the depth of main channel; D (m), the total depth of the compound channel; d(m)= D-h; So, the bed slope, and Qt (l/s), the experimental discharge.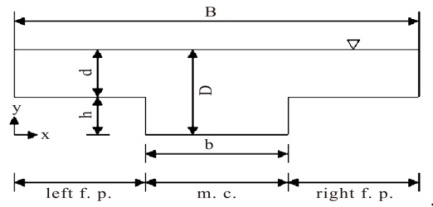 | Figure 1. The definition of the compound channel flow section |
2.3. Equations
The three equations from Field et.al (1998) are,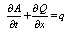 | (1) |
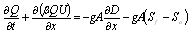 | (2) |
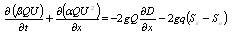 | (3) |
The general forms of energy and momentum coefficients are,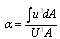 | (4) |
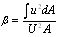 | (5) |
The numerical forms of α and β are,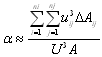 | (6) |
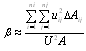 | (7) |
Where Q: the discharge along the flow direction; A: the cross-section; q: the lateral discharge; U: the mean flow velocity. Aij: the grid area; uij: the grid point velocity from the experimental data
2.4. Results of Relationships for α and β:
A. The Relationship of αorβwith 1/Re for different b/B:(1) In main channel: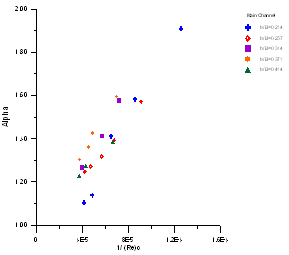 | Figure 2. The relationship between α and 1/Ree in main channel |
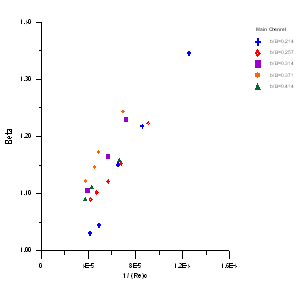 | Figure 3. The relationship betweenβand 1/Ree in main channel |
(2) In flood plain: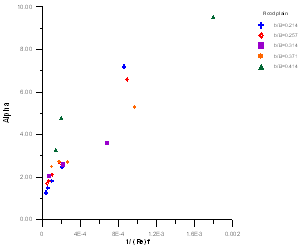 | Figure 4. The relationship betweenαand 1/Ref in flood plain |
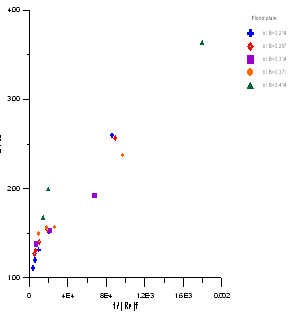 | Figure 5. The relationship betweenβand 1/Ref in flood plain |
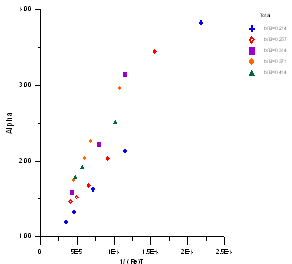 | Figure 6. The relationship betweenαand 1/ReT of total section |
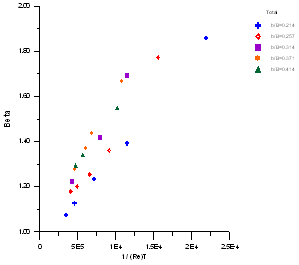 | Figure 7. The relationship betweenβand 1/ReT of total section |
B. The Relationship of αorβwith d/D for different b/B:(1) In main channel: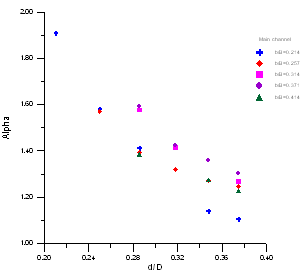 | Figure 8. The relationship between α and d/Din main channel |
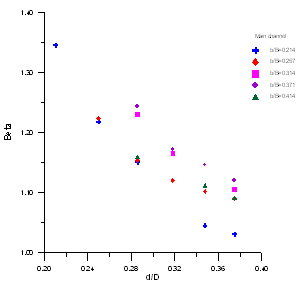 | Figure 9. The relationship betweenβand d/D in main channel |
(2) In flood plain: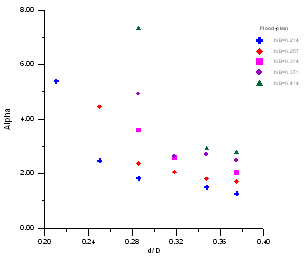 | Figure 10. The relationship between α and d/D in flood plain |
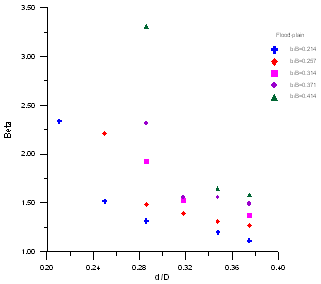 | Figure 11. The relationship betweenβand d/D in flood plain |
(3) In total section: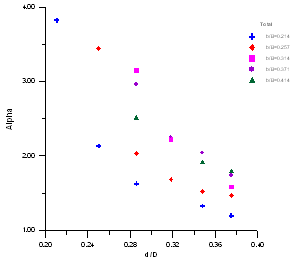 | Figure 12. The relationship between α and d/D of total section |
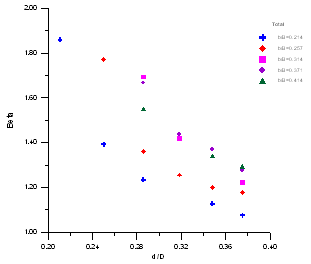 | Figure 13. The relationship betweenβand d/D of total section |
C. Lateral change of different d/D to α with b=:D. Lateral change of different b to α with d/D=0.375: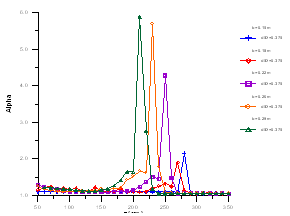 | Figure 15. Lateral change of different b to α |
E. Lateral change of different Ut/U* to α or β with given b/B of total section:(1) For α: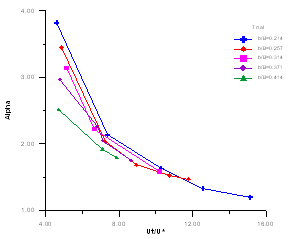 | Figure 16. The variation of α with Ut/U* for total section |
(2) Forβ: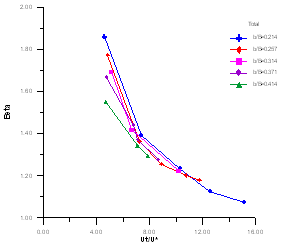 | Figure 17. The variation of β with Ut/U* for total section |
F. 2-D total section Regression of α or β with Ut/U*:(1) For α: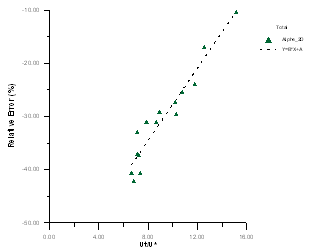 | Figure 18. 2-D total section Regression of α with Ut/U* |
(2) For β:A. For Main-Channel: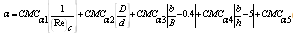 | (8) |
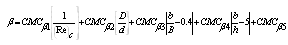 | (9) |
B. For Flood-Plain: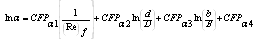 | (10) |
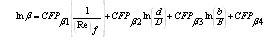 | (11) |
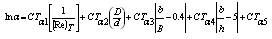 | (12) |
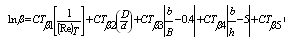 | (13) |
Table 1. Parameters and Regression of Main Channel
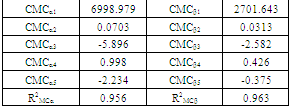 |
| |
|
Table 2. Parameters and Regression of Flood Plain
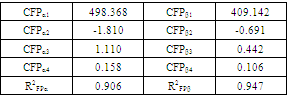 |
| |
|
Table 3. Parameters and Regression of Total Section
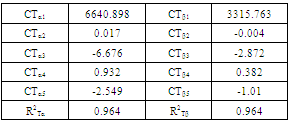 |
| |
|
3. Discussion
When we discuss the flows of natural or artificial channel or pipe, two important factors, Froude’s number and Reynold’s number, are mentioned. For particle initial movement, pipe flow without free surface, friction factor, f, in moody diagram, and the drag coefficient, Cd, the Reynold’s number presents a major function because of small diameter of particle, relatively small hydraulic radius, R=D/4, with slow flow velocity. When the flow velocity is relatively large enough, the particle is suspended without function on channel bed formation which will change the Manning’s n, the friction factor, f, in moody diagram is only function of hydraulically relative thickness, k/D, and the drag coefficient is function of shape cross-section only. With the above mentioned, the Reynold’s number becomes minor factor, meanwhile, the Froude’s number will take over the position, and Hwang[9] also presented this characteristic, and α is decreasing from 1.325 to 1.024 with increasing of d/D from 0.188 to 0.721. In open channel flows, the channel is always wide-shallow (W-S) type and some particular artificial channel is narrow-deep (N-D), the velocity governs the situation. A series of equations presented by Luo[10] will give us some useful information.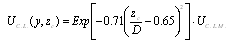 | (14) |
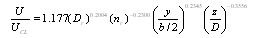 | (15) |
Issam A. Al-khabit[11] also presented the energy coefficient and momentum coefficient in straight compound cross-section flumes with d/D=0.933, 0.867, and 0.800; b=0.20m, 0.30m, and 0.45m; b/h =9, 6, 4.5, 4, 3, 2, and 1.33; Qt =from 3.194 l/s to 100.706 l/s. B=0.67m; h=0.05m, 0.10m, and 0.15m. The energy coefficient is from 1.029 to 1.063 while the momentum coefficient from 1.005 to 1.034, that is, the two coefficients are very close to 1.000 which means the flow situations in the experimental flume can be treated as the single channel with uniform velocity- distribution flows, and the results from our study show extremely different phenomena which are compound channel with varied velocity-distribution 3D flows.
4. Conclusions
(1) The hydraulic flume test was carried out to investigate the relationship of the energy coefficient and momentum coefficient in straight compound channel with the change of Reynold’s number and cross-section shape.(2) The value of both the energy coefficient and momentum coefficient in main channel, flood plain and total section decrease with the increase of water depth and Reynold’s number at the same relative width.(3) The value of both the energy coefficient and momentum coefficient in main channel, flood plain and total section increase with the increase of main channel width at the same relative water depth.(4) At the same Reynold’s number, the value of both the energy coefficient and momentum coefficient in main channel and total section increase with the increase of main channel width.(5) While the Reynold’s number on flood plain is larger than 104, the value of both the energy coefficient and momentum coefficient in flood plain is not significant with cross-section shape.
ACKNOWLEDGEMENTS
Here, I want to show my great appreciation to Mr. Yu-lin, Yen and Prof. Ginn-I, Chang, the master and instructor of National Chia-Yi University for the agreement of publishing our co-research data.
References
| [1] | Knight, D. W., and Demetriou, J. D.,“Floodplain and Mainchannel flow interaction.” Journal of Hydraulic Engineering, ASCE, Vol.109, No. 8, pp.1073-1092(1983) |
| [2] | Knight, D. W., and Hamed, M. E.,“Boundary shear in symmetric compound channels.” Journal of Hydraulic Engineering, ASCE, Vol.110, No. 10, pp.1412-143(1984). |
| [3] | Wormleaton, P. R., Allen, J., and Hadjipanos, P.,”Discharge assessment in compound channel flow.”Journal of Hydraulic Division, ASCE, Proc., Amer. Soc. Civil Engr., Vol. 108, No. HY9, pp.975-994(1982.) |
| [4] | Wormleaton, P. R., and Hadjipanos, P.,“Flow distribution in compound channels.” Journal of Hydraulic Engineering, ASCE, Vol. 111, No. 2, pp.357-361(1985) |
| [5] | Prinos, P., Townsend, R., and Tavoularis, S., “Structure of turbulence in compound channel flows.” Journal of Hydraulic Engineering, ASCE, Vol. 111, No. 9, pp.1246-1(1985) |
| [6] | Myers, W. R. C., “Velocity and discharge in compound channels.” Journal of Hydraulic Engineering, ASCE, Vol. 113, No. 6, pp.753-766(1987) |
| [7] | Myers, W. R. C., and Brennan, E. K., “Flow resistance in compound channels.” Journal of Hydraulic Research, IAHR, Vol.28, No. 2, pp.141-155(1990.) |
| [8] | Field, W. G., Lambert, M. F., and Williams, B. J.,“Energy and momentum in one dimensional open channel flow.” Journal of Hydraulic Research, Vol.36, No. 1, pp.29-42(1998) |
| [9] | Hwang, Y. C., “The flow in compound cross-sectional weirs and rating curve”, Master Thesis, National Cheng Kung University |
| [10] | Luo, C.R. “Hydrodynamic characteristics and applications of compound-channel flows” Proceedings of the 7th IAHR: Stochastic Hydraulics ’96 pp. 535-541(1996) |
| [11] | Issam, A. Al-khabit., “Momentum and kinetic energy coef- ficients in symmetrical rectangular compound cross section flume.” Tr. J. Engineering and Environmental Science Vol.23, pp.187-197(1999) |


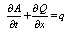
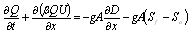
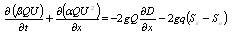
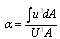
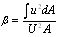
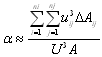
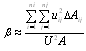
















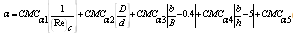
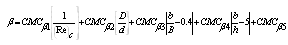
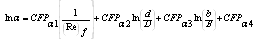
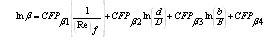
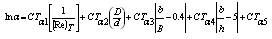
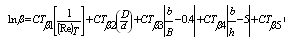
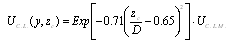
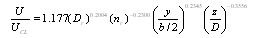
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML

