-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Hydraulic Engineering
2012; 1(2): 1-14
doi: 10.5923/j.ijhe.20120102.01
Characterizing the Impact of Geometric Simplification on Large Woody Debris Using CFD
Jeffrey B. Allen 1, David L. Smith 2
1Information Technology Laboratory, U.S. Army Engineer Research and Development Center, ATTN: CEERD-IE-C, 3909 Halls Ferry Road, Vicksburg, Mississippi, 39180, USA
2Environmental Laboratory, U.S. Army Engineer Research and Development Center, ATTN: CEERD-IE-C, 3909 Halls Ferry Road, Vicksburg, Mississippi, 39180, USA
Correspondence to: Jeffrey B. Allen , Information Technology Laboratory, U.S. Army Engineer Research and Development Center, ATTN: CEERD-IE-C, 3909 Halls Ferry Road, Vicksburg, Mississippi, 39180, USA.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
In general, the presence of large woody debris within river systems creates a desirable effect on fish populations. Experimentally, these positive effects are well documented. Unlike experimental observations; however, numerical simulations of these obstructions are relatively sparse. Those that do exist are in general conducted using idealized simplifications of the actual geometries that they are intended to represent. The purpose of this article is to evaluate the effect of this geometric simplification on the flow field dynamics using numerical simulation. For a given flow field obstruction consisting of a fallen root wad, a series of progressively detailed geometries were created. For each geometry, a shape complexity factor was computed and used for quantifiable comparison purposes. As expected, the localized effect of increased Reynolds number resulted in an increase in turbulent kinetic energy. However, an increase in complexity factor resulted in local and downstream decreases in turbulent kinetic energy. For the cases examined, the results indicated that oversimplifying the complexity of an object can result in significant overpredictions of both velocity magnitude and turbulent kinetic energy.
Keywords: Large woody debris, computational fluid dynamics, turbulence modeling, ecohydraulicsThe method for creating each LWD and subsequently embedding it within the underlying river bed is also outlined in[43]. Figure 5 shows the geometries for e
Article Outline
1. Introduction
- Computational Fluid Dynamics (CFD) models have found widespread use in ecohydraulic assessments[1-4]. One of the most important aspects of using CFD for this purpose is to capture flow field complexity. Eddies and velocity gradients that result from interaction between flow and channel roughness such as large rocks and woody debris are important because invertebrates utilize such environments[5-7]. In general, flow and habitat complexity resulting from the occurrence of large roughness elements and habitat quality may be positively correlated[8].As demonstrated by Crowder and Diplas[2], field data of rivers often captures only the bathymetry while omitting the large scale roughness elements. CFD models typically account for this omission by applying a global roughness value across a large area of the channel. This simplification however, clearly diminishes the local influence of individual rocks and thus mitigates the effective utility of the model for the purposes of ecological assessments. This limitation has been addressed by explicitly representing individual large rocks within the CFD[3,4,9]. Explicit modeling of large woody debris (LWD), on the other hand, has been much more limited. This is not surprising given that detailed field measurement of complex large woody debris and the subsequent computational mesh development can be very difficult. Inadequate meshing practices can leave cells highly distorted, causing numerical diffusion, solution instability, and convergence issues[10].LWD can be a significant source of form drag in a river and can account for 50 percent of the total drag in the channel[11]. LWD plays an important role in stream morphology and is often introduced into streams at reach and watershed scales as part of restoration actions. Given the difficulty in modeling LWD with CFD, it is likely that the hydraulic effects and subsequent linkages to the ecology are not well represented in most CFD models.Previous experimental studies involving turbulent obstructed flow in river systems include the examination of obstructed flow surrounding various boulder profiles[12]. Although these authors naturally encountered local flow variations, they did find similar flow patterns within the turbulent wake of each boulder. They used the results to further discuss how these related to natural channel design and fish habitat. Lacey and Roy[13] also incorporated acoustic velocimetry to characterize turbulent flow around various large roughness elements. They further utilized multivariate regression analysis as a tool to better predict wake turbulence.Complementary to the experimental studies, numerical simulations can also offer an additional means for analyzing turbulent obstructed flow from LWD’s. Unlike the experimental studies mentioned previously, however, a comparable quantity of numerical LWD simulations is severely lacking. While several numerical investigations of turbulent flow in natural stream settings attempt to account for the effects of sediment[14-21], these are generally limited to fairly small grain size distributions. The effects of these flow obstructions are often accounted for by the incorporation of a roughness length. Several field studies have related the total roughness length (ks) to a particle diameter at a certain percentile of the grain size distribution of natural streams[22]. However, there are substantial limitations to utilizing large roughness lengths that may affect the accuracy and stability of solutions. Additionally, most reliable roughness models restrict the roughness length to one-half the near-bed cell thickness[23]. This can become impractical for beds composed of cobbles or even gravels because of the constraints on the amount of flow detail that can be resolved in streams with larger grain sizes. Solution stability and solution accuracy become problematic. If larger near-bed cells are utilized, the cell centroid may no longer fall within the law of the wall region[24]. Modeling LWD’s utilizing roughness length representations remains therefore unfeasible.In natural settings, most LWD boundaries are highly complex and non-uniform. In such cases it is often impractical to model their complex surfaces without using an excessive number of grid elements. Insufficient grid resolution can lead to the near-boundary cells being highly distorted, causing numerical diffusion, solution instabilities, and convergence problems. As a result, relatively few studies have attempted to address the effects of individual flow field obstructions, such as large woody debris[25]. Those that do exist are, in general, conducted using idealized simplifications of the actual geometries that they wish to represent[12]. These geometric simplifications, for example, will often include idealized spheres and cylinders to represent boulders and logs, respectively. The localized and downstream effects of these simplifications on the surrounding flow field when contrasted with non-idealized cases are not well understood. These uncertainties may also be contributing to imprecise conclusions concerning the quality, preservation, and growth of fish habitat in and around these structures.Based on these uncertainties, the objective of this work is to quantify the numerical effect of LWD geometric simplification on the surrounding flow field. Specifically, the local velocity and turbulent kinetic energy will be numerically computed for each of three successively refined LWD geometries. Turbulence modeling will be accomplished via the unsteady Reynolds-averaged Navier-Stokes (URANS), utilizing one of three selected turbulence closer models. For each geometry, a shape complexity factor is computed and used to quantify a relative means for comparison. Preliminary validation, specifically relating to the choice of turbulence closure model, will be first examined through the use of a simplified 3D benchmark study, conducted experimentally by Lyn and Rodi[26] and Lyn et al.[27].
2. Validation Method
- For model validation purposes, the physical experiments performed by Lyn and Rodi[26] and Lyn et al.[27], corresponding to the high Reynolds number, 3D turbulent flow of water over a square cylinder, were selected. This particular application was selected due to its relevance to unsteady viscous flow characteristics behind bluff bodies at high Reynolds’ numbers. Additionally, the study has served as a benchmark for the validation of several different turbulence closure models, including those of DNS, LES and RANS related studies[28-30].One of the most challenging problems associated with turbulence modeling is the accurate prediction of boundary layer flow separation from solid surfaces. While Large Eddy Simulation (LES), has in recent years assumed the primary role in the simulation of these types of flows, a growing number of URANS based turbulence closure models have also shown significant promise. Compared to LES, RANS based models, particularly linear two equation models, although inherently less accurate, are attractive due to their relatively low computational cost, and their seamless amenability to wall functions. Typical LES simulations intrinsically require very high spatial and temporal resolution in order to adequately resolve the large scale turbulent eddies. Additionally, the ensemble averaging that is required for the computation of various mean field quantities, requires relatively long integration times. URANS simulations, in contrast, are significantly less computationally expensive, and require only a few shedding periods in order to converge upon time averaged results. For this study, due to the moderately high Reynolds numbers that are expected, along with the high grid resolution requirements that are necessitated by high fidelity LWD studies involving complex surfaces, the use of a simplified URANS, two-equation turbulence model, combined with the use of wall functions is highly desirable. As previously stated however, the suitability of these simplified models may be questionable for these types of flows. While some authors have claimed their successful utility [28, 31], others have claimed their inadequacy at solving these difficult flow problems[32]. The purpose of this validation section is therefore to evaluate, for the present application involving a square cylinder under a high Reynolds number flow, the applicability of using a two-equation URANS, turbulence closoure approach. If suitable, (via experimental comparisons), the proposed model will then be utilized for the more complicated LWD geometries, which comprise the primary focus of this research.In this study we compare three, URANS, two-equation, linear eddy viscosity turbulence models, with the experimental results of Lyn et al.[26,27]. These turbulence models include the standard k-ε model (SKE)[33], the Re- Normalization Group k-ε model (RNGKE)[34], and the shear- stress transport k-omega model (SSTKW)[35].At high Reynolds numbers the URANS models avoid the need to integrate the equations of motion right down to the wall layer by satisfying the log law:
 | (1) |
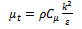 | (2) |
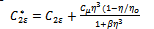 | (3) |
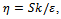 and
and 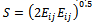 , and the model constants were prescribed as:
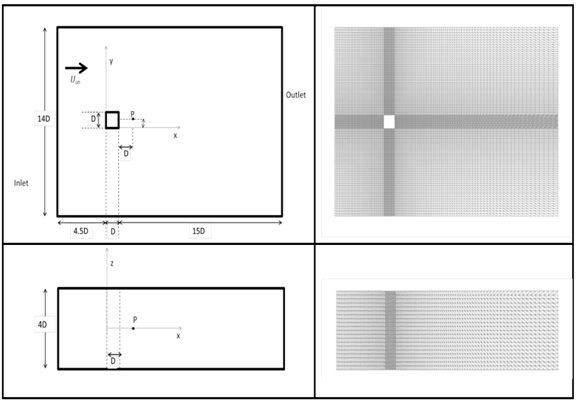
, and the model constants were prescribed as: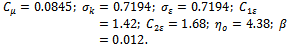 The third and final turbulence closure model used in this study is the SSTKW turbulence model. It was designed by Menter [35] to give improved accuracy in terms of the onset and the amount of flow separation under adverse pressure gradients by the inclusion of the transport turbulent shear stress within the formulation of the eddy-viscosity. Additionally, the model includes a cross-diffusion term in the ω-equation and a blending function to ensure that the model equations perform reasonably within both the near-wall and far-field regions. The performance of this model, particularly with respect to shear separated flows, has been demonstrated in a large number of validation studies, including those of Bardina et al.[37].A square cylinder of side length D (D=0.04m) was situated within a domain of size 21.5D x 14Dx 4D, as shown in Figure 1. As indicated, the square cylinder was located 4.5D aft of the inlet cross section. From previous studies[38,39], the dimensions of the computational domain were deemed sufficiently large to allow for adequate flow evolution in all directions and thus minimize boundary condition effects. A summary of some of the various geometric, inlet and non-dimensional parameters applicable to this study are shown in Table 1.
The third and final turbulence closure model used in this study is the SSTKW turbulence model. It was designed by Menter [35] to give improved accuracy in terms of the onset and the amount of flow separation under adverse pressure gradients by the inclusion of the transport turbulent shear stress within the formulation of the eddy-viscosity. Additionally, the model includes a cross-diffusion term in the ω-equation and a blending function to ensure that the model equations perform reasonably within both the near-wall and far-field regions. The performance of this model, particularly with respect to shear separated flows, has been demonstrated in a large number of validation studies, including those of Bardina et al.[37].A square cylinder of side length D (D=0.04m) was situated within a domain of size 21.5D x 14Dx 4D, as shown in Figure 1. As indicated, the square cylinder was located 4.5D aft of the inlet cross section. From previous studies[38,39], the dimensions of the computational domain were deemed sufficiently large to allow for adequate flow evolution in all directions and thus minimize boundary condition effects. A summary of some of the various geometric, inlet and non-dimensional parameters applicable to this study are shown in Table 1.
|
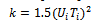 | (4) |
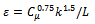 | (5) |
 | (6) |
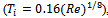 ), and the turbulence length scale (L) was taken as 0.07d, (the factor 0.07 is based on the maximum mixing length in a turbulent pipe flow).The governing equations were solved utilizing OpenFOAM[40] which incorporates the Finite Volume Method (FVM), in which the domain is subdivided into a finite number of small control volumes. FVM uses the integral form of a general convection-diffusion equation over a solution domain subdivided into a finite number of control volumes. For each control volume this equation may be represented as:
), and the turbulence length scale (L) was taken as 0.07d, (the factor 0.07 is based on the maximum mixing length in a turbulent pipe flow).The governing equations were solved utilizing OpenFOAM[40] which incorporates the Finite Volume Method (FVM), in which the domain is subdivided into a finite number of small control volumes. FVM uses the integral form of a general convection-diffusion equation over a solution domain subdivided into a finite number of control volumes. For each control volume this equation may be represented as: | (7) |
3. Validation Results
- Figure 2 shows the time averaged, streamwise velocity component along the domain centerline (
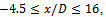 y/D=0.5, z/D=0) comparing the SKE, RNGKE, and the SSTKW turbulence closure models with the experiments performed by Lynn et al.[26,27]. Unless specified otherwise, each of the models were run with the same mesh density, 130 x 120 x 20 cells, corresponding to a near wall resolution of y+=100. As indicated, there is near perfect agreement between the experimental results and all of the turbulence models forward of x/D = 0 (corresponding to the front leading edge of the square cylinder). Aft of the cylinder, (at x/D=1) however, there is noticeable disagreement. As shown, of all the models, the SKE model shows the least agreement with the experimental results. The SKE model predicts the location (x/D) and magnitude (U/Uo) of the minimum velocity to be approximately -0.1 and 2.5, respectively. This is in significant contrast to the experimental results, for which the location and the minimum velocity were measured to be approximately -0.2 and 1.25, respectively. Additionally, the rate at which the velocity returns to its free stream value is also much slower for the SKE model than for all of the other models. The RNGKE model shows some improvement both with respect to the minimum velocity magnitude (-0.18) and a steeper velocity gradient, but the location of the minimal velocity (at ~ x/D=2.5) remains unchanged from the SKE prediction. The SSTKW model with near wall resolution y+ = 100, shows better agreement with experiment than either the SKE or the RNGKE models. It predicts a minimal velocity of approximately -0.2 at a location of 1.7. The return to the free stream velocity is also faster than either model. Increasing the total number of grid elements to 180x180x40 cells, and the near wall resolution to y+=30, (corresponding to the maximum near wall resolution for which log-wall functions remain valid) resulted in better agreement with the experimental data. As indicated, although the SSTKW at y+=30 (hereafter SSTKW2) still under predicts the streamwise velocity aft of x/D=4, the near-wall agreement (
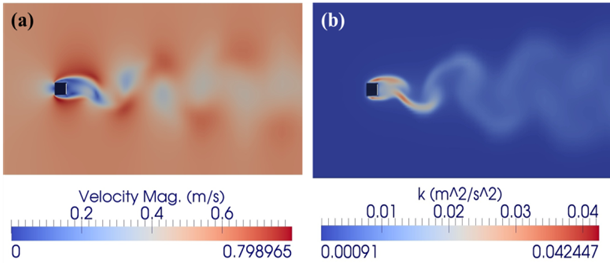
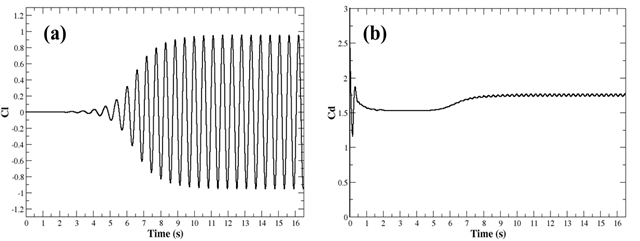
y/D=0.5, z/D=0) comparing the SKE, RNGKE, and the SSTKW turbulence closure models with the experiments performed by Lynn et al.[26,27]. Unless specified otherwise, each of the models were run with the same mesh density, 130 x 120 x 20 cells, corresponding to a near wall resolution of y+=100. As indicated, there is near perfect agreement between the experimental results and all of the turbulence models forward of x/D = 0 (corresponding to the front leading edge of the square cylinder). Aft of the cylinder, (at x/D=1) however, there is noticeable disagreement. As shown, of all the models, the SKE model shows the least agreement with the experimental results. The SKE model predicts the location (x/D) and magnitude (U/Uo) of the minimum velocity to be approximately -0.1 and 2.5, respectively. This is in significant contrast to the experimental results, for which the location and the minimum velocity were measured to be approximately -0.2 and 1.25, respectively. Additionally, the rate at which the velocity returns to its free stream value is also much slower for the SKE model than for all of the other models. The RNGKE model shows some improvement both with respect to the minimum velocity magnitude (-0.18) and a steeper velocity gradient, but the location of the minimal velocity (at ~ x/D=2.5) remains unchanged from the SKE prediction. The SSTKW model with near wall resolution y+ = 100, shows better agreement with experiment than either the SKE or the RNGKE models. It predicts a minimal velocity of approximately -0.2 at a location of 1.7. The return to the free stream velocity is also faster than either model. Increasing the total number of grid elements to 180x180x40 cells, and the near wall resolution to y+=30, (corresponding to the maximum near wall resolution for which log-wall functions remain valid) resulted in better agreement with the experimental data. As indicated, although the SSTKW at y+=30 (hereafter SSTKW2) still under predicts the streamwise velocity aft of x/D=4, the near-wall agreement (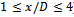 ) is significantly improved.Figure 3 shows velocity and turbulent kinetic energy contours for the simulated square cylinder using SSTKW2. As shown, the vortex shedding motion is well captured. In agreement with the results of Tritico and Hotchkiss[12], who performed physical experiments on actual boulder obstructions, the initial vortex diameters are consistent with the primary obstruction dimensions.Figure 4 shows the time history of the lift and drag coefficients, Cl and Cd, respectively, for SSTKW2. From Figure 4(a), the Cl gradually increases its amplitude of oscillation until approximately t=10s, at which time it reaches a steady oscillation amplitude of approximately ±1. Also from Figure 4(a), the oscillation period was calculated to be 0.5621 seconds, corresponding to a shedding frequency (f) of 1.779 Hz. This resulted in a Strouhal number of 1.33. Figure 4(b) shows the corresponding Cd plot over the same time interval. As indicated, the Cd plot does not show the same amplitude of oscillation as the Cl plot, but instead shows a relatively constant value through the initial 5 seconds of simulation, and thereafter a steady increase in magnitude to an approximate average value of 1.75. At this average value, the amplitude of oscillation is approximately ±0.035.
) is significantly improved.Figure 3 shows velocity and turbulent kinetic energy contours for the simulated square cylinder using SSTKW2. As shown, the vortex shedding motion is well captured. In agreement with the results of Tritico and Hotchkiss[12], who performed physical experiments on actual boulder obstructions, the initial vortex diameters are consistent with the primary obstruction dimensions.Figure 4 shows the time history of the lift and drag coefficients, Cl and Cd, respectively, for SSTKW2. From Figure 4(a), the Cl gradually increases its amplitude of oscillation until approximately t=10s, at which time it reaches a steady oscillation amplitude of approximately ±1. Also from Figure 4(a), the oscillation period was calculated to be 0.5621 seconds, corresponding to a shedding frequency (f) of 1.779 Hz. This resulted in a Strouhal number of 1.33. Figure 4(b) shows the corresponding Cd plot over the same time interval. As indicated, the Cd plot does not show the same amplitude of oscillation as the Cl plot, but instead shows a relatively constant value through the initial 5 seconds of simulation, and thereafter a steady increase in magnitude to an approximate average value of 1.75. At this average value, the amplitude of oscillation is approximately ±0.035.
|
4. Large Woody Debris Method
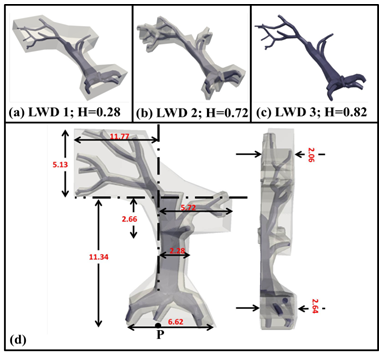
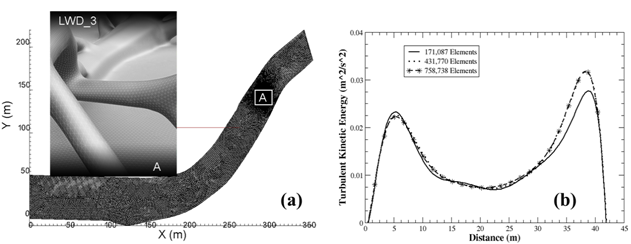
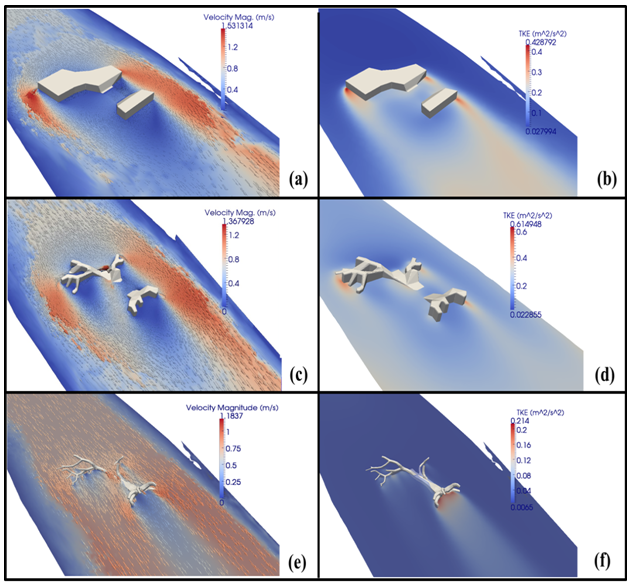
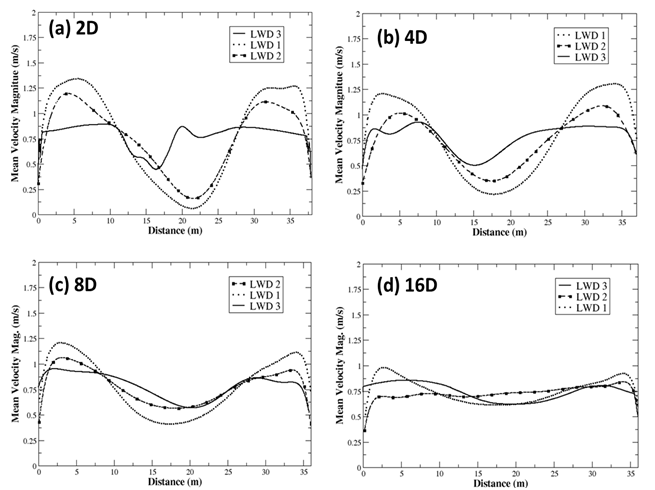
- For context, we selected bathymetric field measurements taken from a 2.4-km (1.5-mile) stretch along the Robinson Restoration project of the Merced River in California[42]. This particular restoration effort was due to the decline over the last decade of both spawning and rearing of fall-run Chinook salmon[42]. A small section of this stretch was considered, extending, as shown in Figure 8(a), over an area of approximately 350 m 200 m. At approximately the 300-m, 150-m downstream location (marked A in Figure 6 (a)), one of a total of three LWD’s (Figure 5 (a-c)) was embedded within the underlying river bathymetry.The river topography was created from a triangulated network of digital terrain mapped (DTM) data in x, y, z format. The points consisted of a coarse set of river cross-sections containing elevations and planar information in Universal Transverse Mercator (UTM) coordinates. The points were then mapped to a grid using the method outlined in a previous study[43]. In brief, the 3DS MAX[44] software tool was heavily utilized and enabled the development of a highly refined uniformly meshed surface mesh.The boundary conditions consisted of a constant velocity inlet of 0.5 m/s. Using the approximate diameter of the tree trunk (2.28 m), this resulted in an average Reynolds number of 21400. Since the water surface elevation did not significantly change over the study section, and since this study is focused on a fully submerged bluff body, the closed lid approach was utilized to model the water surface in lieu of a free surface approach, such as the Volume of Fluid (VOF) method[45]. The outlet boundary condition was implemented using a zero velocity gradient and a constant pressure condition . The terrain boundaries, including the LWD object, were modeled with no-slip boundaries. Bed roughness was approximated from the average sediment sizes which are common to the area (~0.01m), and this roughness height was provide as an input to the turbulent viscosity via a roughness wall function approach[40]. Like the validation studies, the inlet turbulence values associated with the turbulent kinetic energy (k), the turbulent dissipation rate (ε), and the specific dissipation rate (ω) were computed from Equations 4-6. Each LWD geometry was meshed using GAMBI [46], applying a hybrid, non-conformal combination of unstructured tetrahedral and hexahedral elements. A size function application was utilized that allowed for localized mesh refinement at the surface of each LWD. The graded mesh, governed by a first cell height of approximately 0.003 m, resulted for the case of each LWD, a value for the non-dimensional viscous wall unit (y+) of approximately 100 (well within the desired bounds for log law applications 30 < y+< 500). Mesh coarsening of surrounding cells was based on a 10 percent maximum successive increase and culminated in a maximum allowable edge length of approximately 0.61 m. In this manner, the face geometries having the smallest length scales governed the initial size function parameter. For each case a mesh convergence study was conducted to establish the minimum mesh resolution corresponding to grid-independent fluid dynamics. Figure 6(b) shows the cross-stream variation in turbulence kinetic energy associated with the grid resolution of LWD_2. The sampled location pertains to a distance of approximately 0.5D upstream from the obstruction. The mesh resolution, as indicated, beginning with 1.71E5 elements was first increased by a factor of approximately 2.5 to 4.32E5 elements. Subsequently a refinement factor of approximately 1.75 was employed and substantiated sufficient grid independence involving 4.32E5 elements. This same procedure was conducted for the remaining LWD cases, resulting in approximately 2.69E5 elements and 1.49E6 elements for LWD_1 and LWD_3, respectively.From the previous validation results, the SSTKW turbulence closure method was selected due to its superior performance, over the other two turbulence models, for predicting the flow-field evolution over a rectangular cylinder. The governing equations, consisting of the conservation of mass, momentum and the two additional turbulence transport equations, were solved utilizing OpenFOAM[40]. The interpolation to cell faces for the convection terms was performed using a second-order, upwind discretization scheme, while second-order central differences were utilized for the viscous terms. Pressure-velocity coupling was based on the Pressure Implicit with Splitting of Operators (PISO) method[41]. The temporal discretization was conducted using a second order, implicit backward differencing scheme, and an average time step of 1.0e-3 seconds was adaptively maintained in order to keep the maximum Courant number below 1.0. Time averaging of the unsteady results were conducted subsequent to two flow through times (residence times), or 1.4E6 iterations.In contrast to the validation cases, prior to conducting simulations via the highly sensitive SSTKW model, it was necessary to begin each of the three LWD simulations using the SKE approach, approximating the input values for k and epsilon from Equation 4 and Equation 5. After several seconds of simulation, an approximate value for omega could be computed based on Equation 6. In this manner, convergence and numerical instability issues were successfully avoided.
5. Geometric Complexity
- Apart from the apparent qualitative geometric differences between LWD_1, LWD_2, and LWD_3, it is desirable, for the purposes of making quantitative comparisons, to prescribe for each LWD a unique shape complexity factor. Information theory[47] is a useful tool for this purpose. The theory provides a meaningful way to quantify information and describe it within a probabilistic framework. Researchers have applied the theory, for example, to such diverse fields as communications[47], signal processing[48], and medical imaging[49].From information theory[47] we may define a random variable x with a probability density function p(x). We define the complexity factor (H) as:
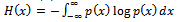 | (8) |
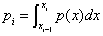 where xi and xi+1 are specific values of x we can write a discrete form of Equation (3) and obtain the following expression for the complexity factor:
where xi and xi+1 are specific values of x we can write a discrete form of Equation (3) and obtain the following expression for the complexity factor: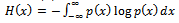 | (9) |
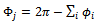 | (10) |
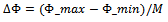 | (11) |
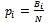 | (12) |
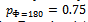 , and
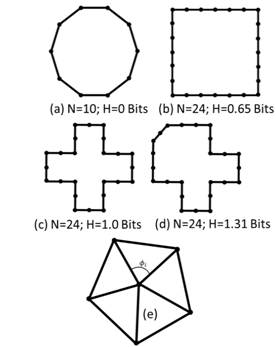
, and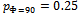 , respectively. Applying Equation 4 (and ensuring log2x is utilized), this leads to a complexity factor of 0.65 bits. By comparison, the decagon of Figure 7(a) contains only one bin for all of its N=10 samples. This figure thus yields a complexity factor of zero, and provides an idealized reference value from which all other shapes (with equivalent samples; N=10) may be compared. Figure 5 (c-d) shows the complexity factors associated with two additional shapes with increasing levels of complexity. As shown, even though the total number of samples remains the same (a necessary prerequisite for making relative comparisons among 2D and 3D objects), the asymmetry of Figure 7(d) contributes to its having a higher complexity factor.
, respectively. Applying Equation 4 (and ensuring log2x is utilized), this leads to a complexity factor of 0.65 bits. By comparison, the decagon of Figure 7(a) contains only one bin for all of its N=10 samples. This figure thus yields a complexity factor of zero, and provides an idealized reference value from which all other shapes (with equivalent samples; N=10) may be compared. Figure 5 (c-d) shows the complexity factors associated with two additional shapes with increasing levels of complexity. As shown, even though the total number of samples remains the same (a necessary prerequisite for making relative comparisons among 2D and 3D objects), the asymmetry of Figure 7(d) contributes to its having a higher complexity factor.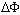 ) and sample size (N) govern the computation of the probability density function (and thus the complexity factor), for relative comparisons among each LWD, we must use consistent numbers of each. For this work we used a constant bin width of 1 deg (M = 360°) and a sample size (N), corresponding to the total number of boundary vertices of LWD_1 (N=24,825).
) and sample size (N) govern the computation of the probability density function (and thus the complexity factor), for relative comparisons among each LWD, we must use consistent numbers of each. For this work we used a constant bin width of 1 deg (M = 360°) and a sample size (N), corresponding to the total number of boundary vertices of LWD_1 (N=24,825).6. Length Scale
- The global Reynolds number (Re) is commonly defined as:
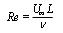 | (13) |
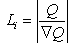 | (14) |
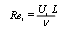 | (15) |
7. Large Woody Debris Results
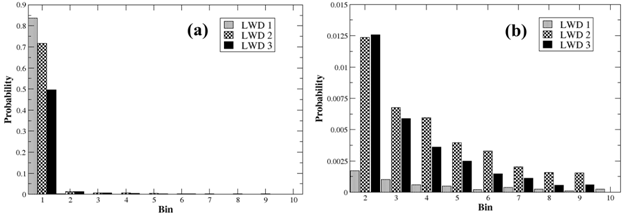
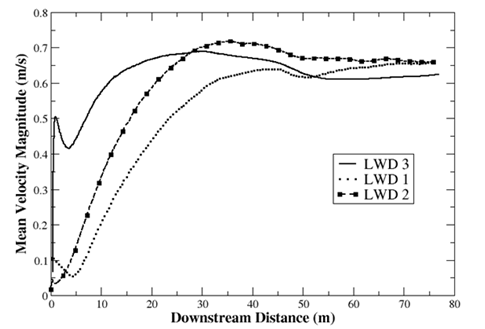
- The resulting complexity factors for each LWD are shown in Table 3. As expected, LWD_1 exhibits the least shape complexity with a complexity factor value of 0.28 bits, while LWD_2 and LWD_3 have complexity factor values of 0.72 bits and 0.82 bits, respectively. The probability plot shown in Figure 8 helps to further clarify the complexity factor differences. As indicated from Figure 8(a), a significant proportion of the LWD bin probabilities are associated with bin 1, corresponding to planar surfaces. Bin one, for example accounts for nearly 85% of LWD_1 surfaces and approximately 72% and 50% for LWD_2 and LWD_3, respectively. Since the remainder of the vertex angles (bins) are associated with non-planar surfaces, it is evident from Figure 8(b), that LWD_2 and LWD_3 contain a much larger proportion of these bin probabilities compared to LWD_1. This larger variance directly corresponds to the increase in complexity factor for LWD_2 and LWD_3. Additional studies of the three LWD’s incorporating larger sample sizes and more refined bin widths were conducted and resulted in negligible complexity factor changes.
|
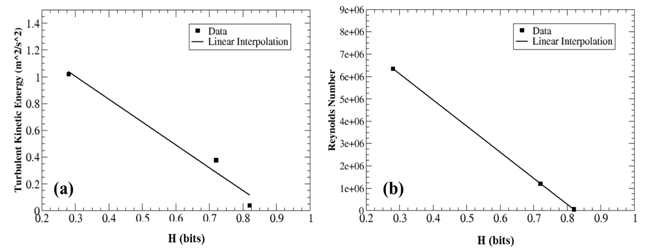 | Figure 10. Plots of locally integrated TKE and Reynolds number (Re) as a function of complexity factor (H). As shown, both the TKE and Re decrease linearly with increasing object complexity |
8. Summary and Conclusions
- The purpose of this article was to evaluate the effect of LWD geometric simplification on the flow-field dynamics as evaluated using CFD. The first step included a validation effort with existing experimental data on two relatively simple boulder geometries consisting of an idealized cylindroid and parallelepiped. The validation tests resulted in reasonable agreement between the numerical and experimental results for both the streamwise velocity and turbulent kinetic energy at a given 1-m cross section. Next a series of three LWD case studies were examined, each representing the same LWD object, but consisting of progressively finer geometric resolution. For each LWD a shape complexity factor was computed based on Information Theory and used quantitatively for relative complexity comparisons. As expected, the localized effect of increased Re resulted in an increase in turbulent kinetic energy. However, for the cases examined, an increase in complexity factor resulted in local decreases in turbulent kinetic energy. The effect of geometric complexity on the velocity magnitude and turbulent kinetic energy was also evident on the downstream flow field. The results indicated that minimizing complexity can result in significant over predictions of both velocity magnitude and turbulent kinetic energy.In summary, the localized and downstream effects of oversimplifying LWD objects within a computational flow field simulation can be significant. Caution should be exercised when undertaking prediction efforts to quantify the effects of these structures when any degree of geometric simplification is conducted.
ACKNOWLEDGEMENTS
- This study was funded in part through the System-wide Water Resources Program (SWWRP).
Nomenclature
- Bi Sampling parameterCμEmpirical constant used in k-ε modeld Semi-major axis (m)H Complexity factor (bits)k Turbulent kinetic energy (m2/s2)ks Roughness length (m)L Length scale (m)LWD Large woody debrisM Number of binsN Total number of samplespiProbability densityQ Representative scalar flow quantityRe Reynolds numberTiTurbulence intensityUVelocity (m/s)
Greek Symbols
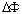 Bin width
Bin width Angle excess (deg.)ε Turbulent dissipation rate (m2/s3)ϕ Subtended wedge angle (deg.)v Kinematic viscosity (m2/s)
Angle excess (deg.)ε Turbulent dissipation rate (m2/s3)ϕ Subtended wedge angle (deg.)v Kinematic viscosity (m2/s)Subscripts
- mag magnitude∞ freestream
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML
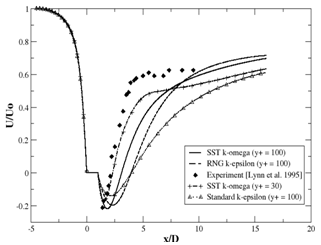
 , y/D=0.5, z/D=0) comparing the SKE, RNGKE, and the SSTKW turbulence closure models with the experiments performed by Lynn et al.[26, 27](1994, 1995). The SSTKW model with near wall resolution, y+=30, resulted in the closest agreement with experiment
, y/D=0.5, z/D=0) comparing the SKE, RNGKE, and the SSTKW turbulence closure models with the experiments performed by Lynn et al.[26, 27](1994, 1995). The SSTKW model with near wall resolution, y+=30, resulted in the closest agreement with experiment