Manoochehr Fathi-Moghadam1, Khosro Drikvandi2
1School of Water Science Eng., Shahid Chamran University, Ahvaz, Iran
2Ministry of Jihad-Keshavarzi, Khoram-Abad, Iran
Correspondence to: Manoochehr Fathi-Moghadam, School of Water Science Eng., Shahid Chamran University, Ahvaz, Iran.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
Manning’ n-value varies in vegetation zones of river and flood plains due to variation of vegetation flexibility and flow depth. Study of river behavior and effect of vegetation on river systems are very important for water intake in pumping stations, water treatment plans and wastewater, fish pools in the river banks and construction of structures such as bridges and diversion channels. Purpose of this research is to develop relationships for estimation of non-submerged vegetation roughness in the flood plains and river banks. Number of 182 experiments was conducted on a laboratory flume and effect of parameters on the roughness coefficient was evaluated. Results show a nonlinear decrease of roughness coefficient with increasing of flow rate. Increase of velocity from 0.2 m/s to 2 m/s make Manning’s coefficient reduces to one third of the first case. Decrease of roughness coefficient with decrease of submergence ratio and density was low compared to velocity effect.
Keywords:
Manning coefficient, Vegetation, Flexibility, Non-Submerged
Cite this paper: Manoochehr Fathi-Moghadam, Khosro Drikvandi, Manning Roughness Coefficient for Rivers and Flood Plains with Non-Submerged Vegetation, International Journal of Hydraulic Engineering, Vol. 1 No. 1, 2012, pp. 1-4. doi: 10.5923/j.ijhe.20120101.01.
1. Introduction
Because of vegetation flexibility in river banks and floodplain, friction factors vary in these areas and are a function of vegetation characteristics and flow conditions. Flow conditions include velocity and depth of flow, and vegetation characteristics are density, flexibility. Vegetation at river banks reduces water flow capacity and causes rising of water level in such areas which may submerge existing structures such as pump stations. Removing vegetation in spite of increasing flow capacity causes instability of the river banks and sometimes endangers the structures, as well as adverse environmental impacts.Vegetation at river banks is either in submerged or non-submerged forms. Grass vegetation and shrubs are submerged forms, and tall trees are non-submerged. Chen (1976) was conducted some experiments on grass vegetation in laboratory flume in laminar flow regime and showed that friction factor decreases with increasing of Reynolds number. Kouwen (1992) applied boundary layer theory to develop a relationship between Manning’s coefficient and product of flow velocity and hydraulic radius. Fisher (1996) showed that vegetation roughness in open channels depend on vegetation type, flexibility, height, density, and their vegetation distribution. Fu-chun and Hsieh (1999) conducted experiments with mane instead of vegetation and concluded that vegetation friction decrease with increasing depth for non-submerged case, while it decreases for submerged cases. (Kouwen and Fathi-Moghadam, 2000) developed a relationship for non-submerged vegetation roughness concerning flow velocity and depth and as well as a vegetation index to characterize type of vegetation. Vegetation index is defined as a function of first module of natural frequency, height, weight and length of plants. Jarvela (2002, 2004) in two studies for determination of flow resistance caused by different combinations of grass, sedges and willows in submerged and non-submerged condition, concluded that changes in depth, velocity, Reynolds number and vegetation density are key factors; and that the maximum friction factor was obtains for low Reynolds number and velocity. The roughness coefficient for leafy trees was about seven times more than leafless trees. Fathi-Moghadam (2006) studied effects of land slope and flow depth on friction factors for non-canalized flow. It was found that friction factors decrease significantly with increase of land slope as result of increase of flow velocity. The friction factor increased with increase of flow depth due to increasing of more submerged elements. Baptist and et al. (2007) compared some methods and solved one-dimensional k-3 equation using an artificial network for calculation of vegetation friction factor Rameshwaran and Shiono (2007) suggested a two- dimensional model for calculation depth- average velocity and shear stress for flow in straight compound channel with flood plain vegetation. The secondary current and friction terms were considered for solution of Navier-Stokes Equations. Fathi-Moghadam (2007) proposed a vegetation index based on first mode of vibration for study of wind flow through four types of coniferous trees. This model can estimate mechanical characteristics of vegetation by considering parameters such as leaf density, shape and flexibility of vegetation. Lai et al. (2008) conducted some flood field measurement on natural rivers and determined flow resistance changes with respect to hydraulic radius variation and flow depth. In this research it has been explained that main channel interaction with flood plains cause the complexity of flow resistance calculation. They have taken two terms of apparent shear stress and mean shear stress in boundary layer and suggested a numerical model for determining the complex friction factor in rivers.Although many studies on effects of vegetation on friction factors, the suggested coefficients are very variable and a constant Manning's value is normally used in practice for all flow and vegetation conditions. This will lead mathematical river models to an incorrect estimation of water level for rivers. This study has been performed on three vegetation types which are normally grown along rivers and in flood plains in arid and semi-arid zones including south parts of . Effect of flow depth and velocity on vegetation roughness is considered.
2. Materials and Methods
As mentioned above, vegetation friction factors because of flexibility is a function of flow condition and vegetation characteristics. Thus for a relationship between Manning’s and Darcy-Wiesbach friction factors, the effective parameters on Non-Submerged vegetation can be assumed as follow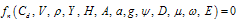 | (1) |
Where Cd is drag coefficient which is equal to ratio of shear velocity to mean flow velocity; V, representing flow velocity; ρ, water density; Y, flow depth; H, vegetation height; A, area of one side of leaf and branches; a , flume bed area covered by vegetation; g, gravity acceleration; ψ, a parameter showing vegetation type and leaf surface; D, vegetation density; μ, water viscosity; ω, first mode of natural frequency for vegetation; E, elasticity of vegetation. Then the dimensionless parameters could be;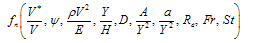 | (2) |
Three last non-dimensional numbers are Reynolds number, Froude number and Strouhal number, respectively. Froude number was less than 1 in all experiments of this study thus it doesn't have any effect on the modelling. The flow is turbulent and steady state is assumed, so Reynolds and Strouhal numbers are not considered here, and Eq. 2 can be reduced as: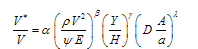 | (3) |
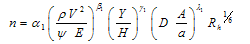 | (4) |
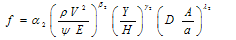 | (5) |
The experiments were conducted in a 12.6m long, 0.5m wide and 0.6m deep glass-walled flume. Discharge water was provided by a centrifuge pump with maximum 55l/s and 10m head. Three vegetation types, including tall and native populous and tamarisk and mixture of populous and tamarisk with four densities, were tested. Natural bush of this vegetation with 35 cm height were installed in regular spaces (in 100% density at 3 cm distances) in different densities in a 2.8 m part of the flume. Flow depths were 11, 13, 16, 20, 28 cm. Slope of flume bed was variable and was changed from 0.005 to 0.02. Flow velocity is measured by a miniature propeller current meter with a propeller diameter of approximately 10 mm (Nixon 430 made in UK) with ,1.5 % resolution. Velocity was measured 30cm upper and lower part vegetation and in 6 points in each cross-section.Using Manning and Darcy –Weisbach equations following relationship were obtained for (f) and (n) coefficients.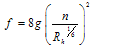 | (6) |
Vegetation density of 100% was defined in such a way that if we look at flume bed from above, bed flume is nearly invisible. Then by reducing of bush numbers, three other densities were defined. The momentum absorbing area was obtained by scanning the pictures taken from flume top. Auto cad and Elvis software were used to count area of black pixels number (A). The method of Fathi-Moghadam (2007) was used to determine the vegetation index 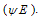
| Table 1. vegetation index and momentum absorption surface obtained from each tree. |
| | Tree type | Vegetation Index | Adsorbed momentum area | | Tamarix | 2.32 | 0.175 | | Populous | 2.02 | 0.150 |
|
|
3. Results and Discussions
The estimated vegetation index and momentum absorbing area for the tested vegetation species are shown in Tab. 1. A considerable effect of velocity on Manning n-value for different ratio of submergence is shown on Figs. 1 and 2.Effect of ratio of submergence on Manning's n-value for different channel velocity is shown in Fig. 3 for populous (density of 50%). Friction coefficient increases with ratio of submergence due to increase of more roughness elements.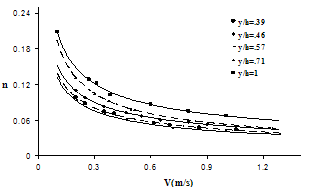 | Figure 1. Manning’s coefficients versus velocity and ratio of submergence for 100% density (Populous). |
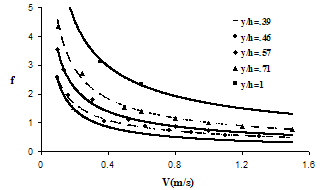 | Figure 2. Darcy-Weisbach friction factor (f) versus velocity and ratio of submergence for 100% density (Tamarix). |
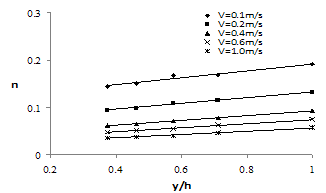 | Figure 3. Manning’s coefficients changes with submerge ratio in similar velocity in populous in density50%. |
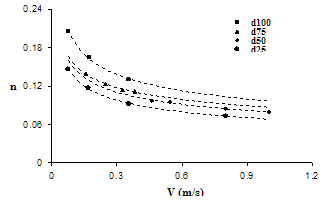 | Figure 4. Manning's n versus velocity for different density (Tamarix). |
Figure 4 shows considerable increase of Manning's n-value with increase of vegetation density. Figure 5 also illustrates a linear increase of n-value with increase of density as it was with flow depth in Fig. 3.Figure 6 shows variation of n-value with velocity for populous and tamarix. A higher value of n for Tamarix reveal more rigidity of tamarix than populous.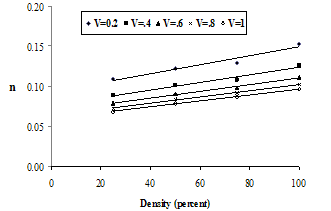 | Figure 5. Effect of vegetation density on Manning’s coefficients for tamarisk. |
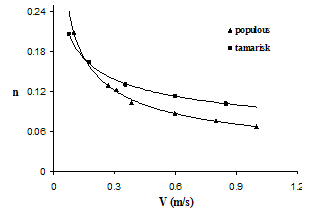 | Figure 6. Comparing effect of vegetation type on Manning’s coefficients (tamarisk and populous, 100% density). |
Using SPSS and vegetation index for tamaix and populous (Table 1), results of all flume experiments in this study were incorporated into Eqs. 4 and 5 and following equations for calculation of friction coefficients (n and f) are correlated.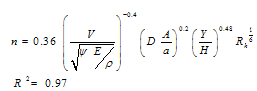 | (7) |
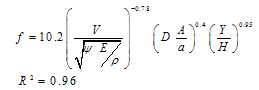 | (8) |
Equations 7 and 8 can be used in river hydraulic models for estimation of friction coefficients (n and f) at any flow and vegetation conditions in metric system of units.
4. Conclusions
Equation 7 and 8 have been developed based on experimental results and can be used to estimate friction factor coefficients for non-submerged vegetation along rivers and in flood plains with minimum required parameters. Equations in agreement with previous works (Kouwen and Fathi-Moghadam, 2000); Jarvela (2004) confirm consider effect of flow and vegetation condition on roughness coefficients. The coefficients decrease with increase of flow velocity, while it increases linearly with increase of flow depth and density due to submergence of more roughness elements. This proofs existence of an additive property for increase of roughness elements. The vegetation index showed to be a suitable parameter to characterize mechanical properties and behavior of vegetation against the flow.
ACKNOWLEDGEMENTS
The authors would like to acknowledge Chamran University of Ahwaz and the Centre of Excellence on Operation Management of Irrigation and Drainage Networks for financial support and facilitation of the experiments. Acknowledgement is also extended to the Research and Standard Office of Khuzistan Water and Power Authority (KWPA).
References
| [1] | Baptist MJ (2007). On inducing equations for vegetation resistance. Journal of Hydraulic Research, 45 (4): 435-450 |
| [2] | Chen CI (1976). Flow resistance in broad shallow grassed channels. Journal of the Hydraulics division, ASCE, 102(3): 307-322 |
| [3] | Fathi-Moghadam M (2006). Effects of Land slope and flow depth retarding flow in Non-submerge vegetated Land. Journal of Agronomy, 5(3): 536-540 |
| [4] | Fathi-Moghadam M (2007). Physical properties of vegetation for resistance to flow .Journal of Agronomy, 6: 194-198 |
| [5] | Fisher KR (1996). Hand book for assessment of hydraulic performance of environmental channels. Report SR490, draft .HR Wallingford, Wallingford, GB, 346 pages |
| [6] | Fu-chun W, and Hsieh WS (1999). Variation of roughness coefficients for un submerged and submerged vegetation” Journal of Hydraulic Engineering, 125 (9): 934-942 |
| [7] | Jarvela J (2002). Flow resistance of flexible and stiff vegetation; a flume study with natural plants. Journal of Hydrology 269(1-2): 44-54 |
| [8] | Jarvela J (2004). Determination of resistance caused by non-submerged woody vegetation.. Int. J. River Basin Mangt. 2(1): 61-70 |
| [9] | Kouwen N (1992). Modern approach to design of grassed channels. Journal of Irrigation and Drainage Engineering, ASCE, 118(5): 733-743 |
| [10] | Kouwen N, Fathi-Moghadam M (2000). Friction factors for coniferous trees along rivers. Journal of Hydraulic Engineering 126(10): 732-740 |
| [11] | Lai SH, Bessaih N, Ling LP., Ghani, AA, and Seng MY (2008). Determination of apparent and composite friction factors for flooded equatorial natural rivers. Intl. Journal. River Basin Management. 6 (1). 3-12 |
| [12] | Rameshwaran P., and Shiono K (2007). Quasi two- dimensional model for straight overbank flows through emergent vegetation on floodplains. Journal of Hydraulic Research, 45 (3):.302–315 |

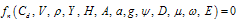
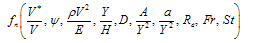
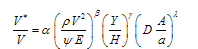
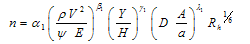
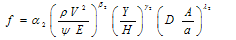
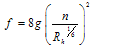






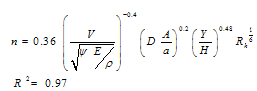
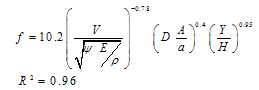
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML