| [1] | Ablowitz, M.J. and P.A. Clarkson, 1991. Solitons, nonlinear evolution equations and inverse scattering, Cambridge: Cambridge University Press. |
| [2] | Hirota, R., 2004. The Direct Method in Soliton Theory, Cambridge Univ. Press. |
| [3] | Wazwaz, A. M., 2006. Travelling wave solutions for combined and double combined sine-cosine-Gordon equations by the variable separated ODE method, Appl. Math. Comput, 177: 755-760. |
| [4] | Dehghan, M. and J. Manafian, 2009. The solution of the variable coefficients fourth–order parabolic partial differential equations by homotopy perturbation method, Z. Naturforsch, 64: 420-430. |
| [5] | Dehghan, M., J. Manafian and A. Saadatmandi, 2010. The solution of the linear fractional partial differential equations using the homotopy analysis method, Z. Naturforsch, 65a: 935-949. |
| [6] | Dehghan, M., J. Manafian and A. Saadatmandi, 2010. Solving nonlinear fractional partial differential equations using the homotopy analysis method, Num. Meth. Partial Differential Eq. J, 26: 486-498. |
| [7] | He, J. H., 1999. Variational iteration method a kind of non-linear analytical technique: some examples, Int. J. Nonlinear Mech, 34: 699-708. |
| [8] | Dehghan, M., J. Manafian and A. Saadatmandi, 2010. Application of semi–analytic methods for the Fitzhugh–Nagumo equation, which models the transmission of nerve impulses, Math. Meth. Appl. Sci, 33: 1384-1398. |
| [9] | Dehghan, M. and J. Manafian, 2011. Study of the wave-breaking’s qualitative behavior of the Fornberg-Whitham equation via quasi-numeric approaches, Int. J. Num. Methods Heat Fluid Flow, to appear in 2011. scattering, Cambridge: Cambridge University Press. |
| [10] | Fan, E., 2000. Extended tanh-function method and its applications to nonlinear equations, Phys. Lett. A, 277: 212-218. |
| [11] | Menga, X. H., W. J. Liua, H. W. Zhua, C. Y. Zhang and B. Tian, 2008. Multi-soliton solutions and a Bäcklund transformation for a generalized variable-coefficient higher-order nonlinear Schrö dinger equation with symbolic computation, Phys. A, 387: 97-107. |
| [12] | Manafian Heris, J. and M. Bagheri, 2010. Exact Solutions for the modified KdV and the Generalized KdV Equations via Exp-Function Method, J. Math. Extension, 4: 77-98. |
| [13] | He, J. H., 2006. Non-perturbative method for strongly nonlinear problems. Dissertation, De-Verlag im Internet GmbH, Berlin. |
| [14] | He, J.H. and X.H. Wu, 2006. Exp–function method for nonlinear wave equations, Chaos, Solitons Fractals, 30: 700-708. |
| [15] | Dehghan, M., J. Manafian and A. Saadatmandi, 2011. Application of the Exp-function method for solving a partial differential equation arising in biology and population genetics, Int. J. Num. Methods Heat and Fluid Flow, 21: 736-753. |
| [16] | Dehghan, M., J. Manafian and A. Saadatmandi, 2011. Analytical treatment of some partial differential equations arising in mathematical physics by using the Exp-function method, Int. J. Modern Physics, B, 25: 2965-2981. |
| [17] | Wang, M., X. Li and J. Zhang, 2008. The (G'/G )-expansion method and travelling wave solutions of nonlinear evolution equations in mathematical physics, Phys. Lett. A, 372: 417-423. |
| [18] | Zhang, J., X. Wei and Y. Lu, 2008. A generalized (G'/G )-expansion method and its applications evolution equations in mathematical physics, Phys. Lett. A, 372: 3653-3658. |
| [19] | Zhang, S., J. L. Tong and W. Wang, 2008. A generalized (G'/G )-expansion method for the mKdV equation with variable coefficients, Phys. Lett. A, 372: 3653-3658. |
| [20] | Bekir, A., 2008. Application of the (G'/G )-expansion method for nonlinear evolution equations, Phys. Lett. A, 372: 3400-3406. |
| [21] | Micu, S., 1999. On the controllability of the linearized Benjamin–Bona–Mahony equation, SIAM J Control Optim, 29: 1677–1696. |
| [22] | Bona, J., 1981. On solitary waves and their role in the evolution of long waves. Applications of nonlinear analysis, Boston, MA: Pitman. |
| [23] | Wazwaz, A. M., 2008. The extended tanh method for new compact and noncompact solutions for the KP–BBM and the ZK–BBM equations, Chaos Solitons Fractals, 38: 1505-1516. |
| [24] | Yusofoǧlu, E., 2008. New solitonary solutions for the MBBM equations using Exp-function method, Phys Lett A, 372: 442-446. |
| [25] | Benjamin, T.B., J.L. Bona and J.J. Mahony, 1972. Philos. Trans. R. Soc. London, Ser. A, 272: 47-55. |
| [26] | Saut, J.C. and N. Tzetkov, 2004. Appl. Math. Res. Express, 1: 1-11. |
| [27] | Varlamov, V. and Y. Liu, 2004. Discrete Dynam. Syst, 10: 731-739. |

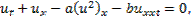
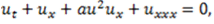
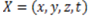 and dependent variable
and dependent variable 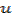
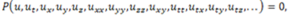
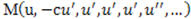
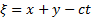 is wave variable. Also, c is constant to be determined later.Step 2. We seek its solutions in the more general polynomial form as follows
is wave variable. Also, c is constant to be determined later.Step 2. We seek its solutions in the more general polynomial form as follows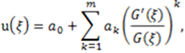
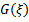 satisfies the second order linear ordinary differential equation (LODE) in the form
satisfies the second order linear ordinary differential equation (LODE) in the form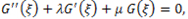
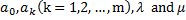 are constants to be determined later,
are constants to be determined later, 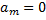 , but the degree of which is generally equal to or less than
, but the degree of which is generally equal to or less than 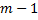 , the positive integer m can be determined by considering the homogeneous balance between the highest order derivatives and nonlinear terms appearing in Eq. (2.2). Step 3. Substituting (2.3) and Eq. (2.4) into Eq. (2.2) with the value of m obtained in Step 1. Collectingthe coefficients of
, the positive integer m can be determined by considering the homogeneous balance between the highest order derivatives and nonlinear terms appearing in Eq. (2.2). Step 3. Substituting (2.3) and Eq. (2.4) into Eq. (2.2) with the value of m obtained in Step 1. Collectingthe coefficients of 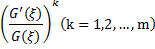 , then setting each coefficient to zero, we can get a set of over-determined partial differential equations for
, then setting each coefficient to zero, we can get a set of over-determined partial differential equations for 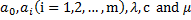 with the aid of symbolic computation Maple 12.Step 4. Solving the algebraic equations in Step 3, then substituting
with the aid of symbolic computation Maple 12.Step 4. Solving the algebraic equations in Step 3, then substituting 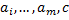 and general solutions of Eq. (2.4) into (2.3) we can obtain a series of fundamental solutions of Eq. (2.1) depending of the solution
and general solutions of Eq. (2.4) into (2.3) we can obtain a series of fundamental solutions of Eq. (2.1) depending of the solution 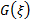 of Eq. (2.4).
of Eq. (2.4). 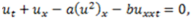
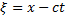 reduces it to an ODE
reduces it to an ODE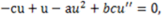
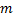 , we balance the linear term of the highest order
, we balance the linear term of the highest order 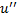 with the highest order nonlinear term
with the highest order nonlinear term 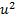 in Eq. (3.2), along with (2.3) we get
in Eq. (3.2), along with (2.3) we get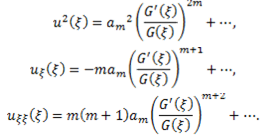
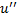 with
with 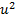 in Eq. (3.2), based on (3.3) we required that
in Eq. (3.2), based on (3.3) we required that 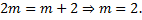 We can suppose that the solutions of Eq. (3.1) is as follows
We can suppose that the solutions of Eq. (3.1) is as follows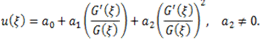 (3.4)and therefore
(3.4)and therefore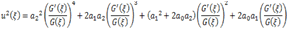
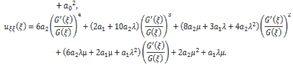
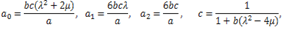
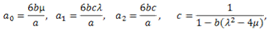
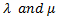 are arbitrary constants. Substituting (3.7) and (3.8) into expression (3.4), can be written as
are arbitrary constants. Substituting (3.7) and (3.8) into expression (3.4), can be written as 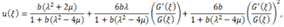
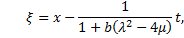
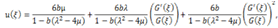
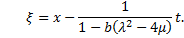 Substituting the general solutions of Eq. (2.4) into (3.9) and (3.10) we have three types of exact solutions of Eq. (3.1). I. When
Substituting the general solutions of Eq. (2.4) into (3.9) and (3.10) we have three types of exact solutions of Eq. (3.1). I. When 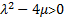 , we obtain hyperbolic function solution
, we obtain hyperbolic function solution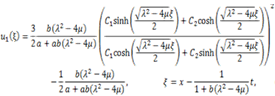
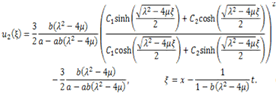
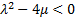 , we have trigonometric function solution
, we have trigonometric function solution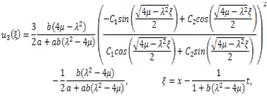
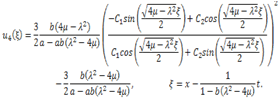
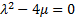 , we get rational solution
, we get rational solution
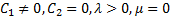 , then solution (3.11) and (3.12), respectively, give:
, then solution (3.11) and (3.12), respectively, give:
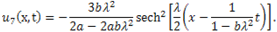
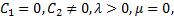 then (3.11) and (3.12) give respectively
then (3.11) and (3.12) give respectively

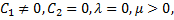 then (3.13) and (3.14) can be written as respectively
then (3.13) and (3.14) can be written as respectively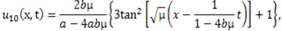
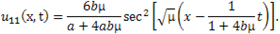
 then (3.13) and (3.14) can be written as respectively
then (3.13) and (3.14) can be written as respectively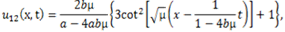
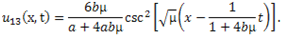
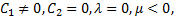 then (3.11) and (3.12) give respectively
then (3.11) and (3.12) give respectively
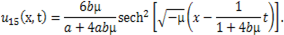
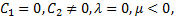 then (3.11) and (3.12) give respectively
then (3.11) and (3.12) give respectively
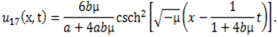
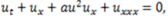
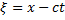 reduces it to an ODE
reduces it to an ODE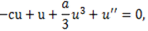
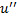 with the highest order nonlinear term
with the highest order nonlinear term 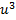 in Eq. (4.2), and by using Eq. (2.3) we will have
in Eq. (4.2), and by using Eq. (2.3) we will have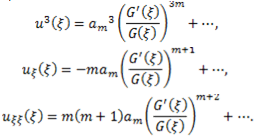
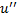 with
with 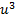 in Eq. (4.2), based on (4.3) we required that
in Eq. (4.2), based on (4.3) we required that 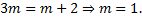 We can suppose that the solutions of Eq. (4.1) is as follows
We can suppose that the solutions of Eq. (4.1) is as follows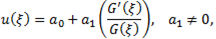
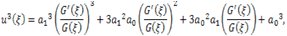
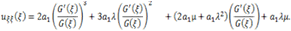
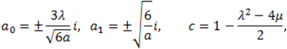
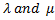 are arbitrary constants. Substituting (4.7) into expression (4.4), can be written as
are arbitrary constants. Substituting (4.7) into expression (4.4), can be written as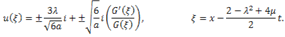
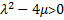 we obtain hyperbolic function solution
we obtain hyperbolic function solution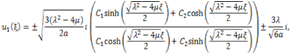
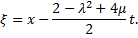 II. When
II. When 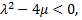 we have trigonometric function solution
we have trigonometric function solution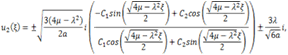
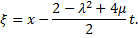 III. When
III. When 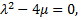 we get rational solution
we get rational solution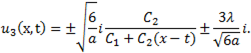
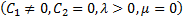 or
or 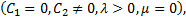 then (4.9) gives
then (4.9) gives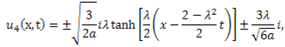
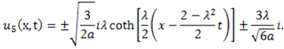
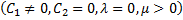 or
or 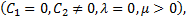 then (4.10) becomes respectively
then (4.10) becomes respectively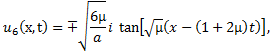
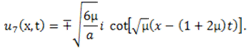
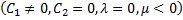 or
or 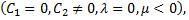 then (4.9) gives respectively
then (4.9) gives respectively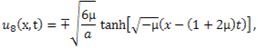
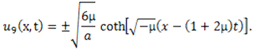
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML