Dodik Siswantoro 1, I Gusti Ngurah Agung 2
1Department of Accounting, Universitas Indonesia, Depok, 16424, Indonesia
2Department of Management, Universitas Indonesia, Depok, 16424, Indonesia
Correspondence to: Dodik Siswantoro , Department of Accounting, Universitas Indonesia, Depok, 16424, Indonesia.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
Most researchers in accounting use models having dummy independent variables to divide the research objects into two or more groups of objects or individuals. In other researches, they employ more than one variable in the model. However, the dummy variable(s) that stand alone may implicate improper correlations between the numerical independent variables with the corresponding dependent variable within the groups, namely the numerical independent variables have the same effects on the dependent variables within all groups of individuals. To overcome this problem, interaction factors between the dummies and the numerical variable(s) should be used as additional independent variables. So that the models considered would be heterogeneous regression models. It is found, only very few researchers employ the heterogeneous regression models, or the interaction models in general, in top accounting journal, recently. This paper attempts to show that the absence of interaction models may mislead the causal relationship between the independent and dependent variables, specifically between the numerical variables, of the models. The main objective of this paper is to present the importance of interaction models should be applied as the basic statistical models. It is expected that this paper can contribute for a better understanding to the students and less experience researchers in developing the statistical models, in various field of studies.
Keywords:
Accounting Model, Interaction Models, Causal Relationship
Cite this paper:
Dodik Siswantoro , I Gusti Ngurah Agung , "The Importance of the Effect of Exogenous Interaction Factors on Endogenous Variables in Accounting Modeling", International Journal of Finance and Accounting , Vol. 1 No. 6, 2012, pp. 194-197. doi: 10.5923/j.ijfa.20120106.08.
1. Introduction
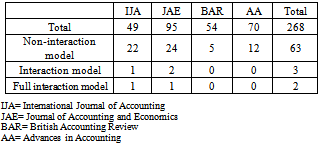
It seems that there is no procedural standard when we use one or two dummy variables in the accounting model for research. Some books of SPSS or Eviews do not treat this specifically when there is a dummy variable used. Actually, when we employ a dummy variable we assume that there is a difference between the groups of the research objects generated by the dummy variable. In fact, some researchers may not consider those differences to present their models. This is actually important tools to see whether the dummy variable is needed or otherwise.This paper tries to see the importance of the counting model having interaction independent variable(s), in a theoretical sense, since a number of additive counting models have been presented in accounting journal recently. For this paper, we have observed a total of 268 papers in four international journals, namely the International Journal of Accounting (IJA), Journal of Accounting and Economics (JAE), British Accounting Review (BAR) and Advances in Accounting (AA), from 2008 to 2010. There are a total of 63 papers use dummy variable, but only five are using interaction models, where two of the five interaction models are full interaction models, as presented in table 1.Note that this table shows that the only Journal of Accounting and Economics and International Journal of Accounting have been presenting the interaction models. This may be caused the need of categorization to differentiate the inherent characteristics for each journal.Table 1. The total number of models by their classification, presented in four journals, observed in the last three years
 |
| |
|
An interaction models, including the heterogeneous regression model, should be considered as the very basic statistical model, in general. Since if we have several exogenous (cause, source, upstream or independent) variables, then it can easily be identified, in a theoretical sense, that the effect of an exogenous variable should depend on at least one of the others. Hence, the main objective of this paper is to present the basic theoretical concepts of heterogeneous regression models, the interaction models in general. Furthermore, it is expected that this paper would contribute for a better understanding to the students, as well as less experience researchers, in developing the statistical models in various field of studies.
2. Basic Theoretical Concept of the Interaction Models
Corresponding to the interaction models, Agung (2010, 2009, 2008 and 2006) has demonstrated the applications of interaction models, even for the models having two or three independent variables, either categorical or numerical independent variables, where each categorical should be transformed to dummy variables. In fact, heterogeneous regressions model was presented by Johnson & Neyman in 1936 (quoted by Huitema, 1980, p.270). So that the interaction models have been applied for more than 75 years, hence, the suggestion for using interaction model(s) may be important issue for enriching the research. This section presents the basic theoretical concept of the interaction models, which could easily be extended to higher order interaction models with many independent variables.
2.1. Models Having Two Dichotomous Independent Variables
Having a numerical endogenous variable Y, including the zero-one problem indicator, and two dichotomous exogenous variables A and B, then the model should be considered is a two-way ANOVA model. Note that the dichotomous variables A and B, respectively, should be represented using pairs of dummy variables, namely (DA1, DA2), and (DB1, DB2), then the following alternative two-way interaction models can be applied (Agung, 2010).(a) A pure interaction model: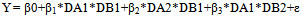 | (1) |
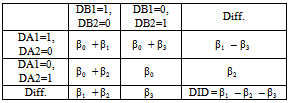
Table 2. Difference in differences model 1
 |
| |
|
By applying pure interaction model would cause (β11 – β22 – β3)ddifference in differences (DID). Model gives meaningful result in DID. (b) A non-hierarchical model: 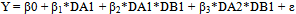 | (2) |
Model with non-hierarchical would result different DID (β22 – β3 ). Model with dichotomous variable should interact with all other variable to give better DID. (c) Another non-hierarchical model: 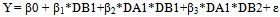 | (3) |
(d) A full-factorial or hierarchical model: 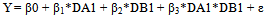 | (4) |
Table 3. Difference in differences model 2
 |
| |
|
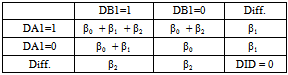
Note that all models should have four parameters, namely β0, β1, β2, and β3 which equals to the number of cells generated by the factors A and B, and they are representing the effect of the factor A (or B) on Y depends on the factor B (or A), in a theoretical sense. So that, the following additive model should be considered an improper or worst model.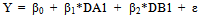 | (5) |
In other words, this model has hided assumptions, in addition to the basic assumption of its error terms, since the model has only three parameters for the four cells generated by the factors A and B. DID would give 0 which means meaningless as dichotomous variables do not have each interaction. Dichotomous variable is the lowest group under ordinal, interval and ratio data. Therefore, it should be grouped with interaction for specific case. Table 4. Difference in differences model 5
 |
| |
|
2.2. Models Having a Numerical and a Dichotomous Independent Variables
Having a numerical endogenous variable Y, including the zero-one problem indicator, a numerical exogenous variable X, and a dichotomous exogenous variables A, then in general X has different effects on Y between the two groups generated by the factor A. In this case then the simplest heterogeneous regressions can be applied, which has the following alternative forms.(a) A model using a dummy variable with intercept parameter: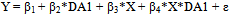 | (6) |
(b) A model using two dummy variables without intercept parameter.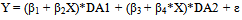 | (7) |
2.3. Models Having Two Numerical Independent Variables
It is recognized that if we have a numerical endogenous variable Y, and two numerical exogenous variables X1 and X2, then in most cases the linear effect of an exogenous variables on Y, depends of the other exogenous variable, in a theoretical sense. Thence, the interaction factor X1*X2 should be used as an independent variable of any models considered. In this case, it is recommended to apply the following simple alternative two-way interaction models.(a) A hierarchical or full interaction model: 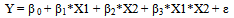 | (8) |
(b) Alternative reduced models: 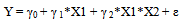 | (9) |
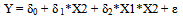 | (10) |
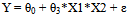 | (11) |
3. Interaction Models Presented in Selected Papers
This section presents selected papers from international journals that use interaction models. It will be explained the significant effect of interaction model, and the need of different test for each categorical variable. This is important to see whether the categorization of dummy variable is needed or otherwise. The complex problem may arise if more than one dummy variable are employed, the matrix table may be useful to see different test.First, Francis & Martin (2010) present a three-way interaction model (12) having a single dummy variable (D), defined as D=1 if the return is negative (R < 0) and D=0 if otherwise, and 24 parameters. In other words, the model has 23 independent variables Note that the model has two-interaction variables, such as Di,t-1 * Ri,t-1, AcqCARi,t * Di,t-1 and AcqCARi,t * Ri,t-1, and three-way interaction variables: AcqCARi,t * Di,t-1 * Ri,t-1 and Leveragei,t-1 * Di,t-1 * Ri,t-1. Thence, it can be concluded that the numerical independent variables have different effects on Xi,t-1 between the groups indicated by D=1 and D=0. But they do not apply different test between the groups.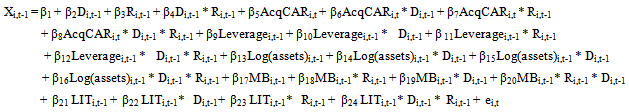 | (12) |
Kann & Watts (2009) also employ a three-way interaction model (13). It is presented that each of the interaction independent variables (Ret*Size), (Ret*M/B), (D*Ret), (D*Ret*Size), (D*Ret*Lev) and (D*Size) has a significant adjusted effects on X. But they do not apply different test between the groups indicated by the dummy variable D.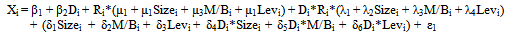 | (13) |
Shah, et.al (2009) employ a two-way interaction model (14) using S as a dummy variable, such that S=1 if the firm classified as large, S=0 otherwise. Note that the two-way interaction between S and each of the other variables , namely A, RD, E, BV, D and CC, indicate that the six variables have different effects on MV between the two groups of the firms indicated by the dummy variable S.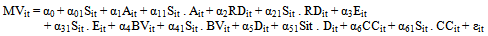 | (14) |
Jermias & Setiawan (2008) utilize a full interaction model (15) to see the effect of three independent variables to performance (Perform). They use two dummy variables, hierarchy and control system. In their paper, they do not conduct different test for each dummy variable, so we hardly to know whether this categorization is needed or otherwise. But all interaction variables show significant effect to Performance for dichotomous control. In this case, only (Control*Participation) variable that do not show significant effect. 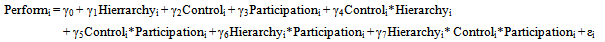 | (15) |
Lastly, Hugon & Muslu (2010) adopt a full interaction model, but the dummy is actually under interaction model for other variable (REV). Only variables (REV*INS) and (REV*CONSERV*INS) show significant effect to CAR. 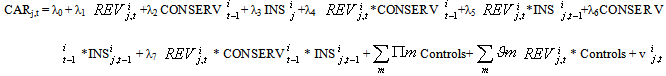 | (16) |
From journals that use accounting model, we can see interaction variable can give significant effect to the model or dependent variable. Based on the interaction model, it can be shown that the absence of interaction model may mislead the analysis.
4. Conclusions
In a theoretical sense, interaction model should be applied if we have at least two cause or source variables, especially if we have categorical independent variable(s) which should be represented using dummy variables. This is because a dummy variable is a tool to see whether there is a significant effect among variables or otherwise. Thus, we should interact it to other variables as it attach to them directly. Mapping or matrix model may be a good explanation to see this. Research results show that only few papers adopt a full interaction model when they employ a dummy variable/s. Significant effect of interaction variable may show that the interaction model is needed when we use a dummy variable(s).Even though the interaction models are very importance models, we would never present empirical models using all possible interactions, if the models have three or more numerical independent variables. So that the researchers should select some important interactions, based on their best judgments, supported by their knowledge and experiences.
ACKNOWLEDGEMENTS
This paper is a revision of the paper, which has been presented at The 3rd International Accounting Conference held by Universitas Indonesia, 27 - 28 October 2010. Bali, Indonesia.
References
| [1] | Agung, I. G. N., Penerapan model rerata-sel multivariat dan model ekonometri dengan SPSS. Jakarta: Yayasan SAD Satria Bhakti, 2006. |
| [2] | Agung, I. G. N., Manajemen penulisan skripsi, tesis dan disertasi statistika: Kiat-kiat untuk mempersingkat waktu penulisan karya ilmiah yang bermutu. (4th ed.). Jakarta: PT RajaGrafindo Persada, 2008. |
| [3] | Agung, I. G. N., Time series data analysis using E-Views. Singapore: John Wiley & Sons, 2009. |
| [4] | Agung, I. G. N., Cross section and experimental data analysis using E-Views. Singapore: John Wiley & Sons, 2011. |
| [5] | Artur Hugon, Volkan Muslu, “Market demand for conservative analysts”, Journal of Accounting and Economics, vol. 50, pp. 42–57, 2010. |
| [6] | Jere R. Francis, Xiumin Martin, “Acquisition profitability and timely loss recognition”, Journal of Accounting and Economics, vol. 49,pp.161–178, 2010. |
| [7] | Johnny Jermias, Trisnawati Setiawan, “The moderating effects of hierarchy and control systems on the relationship between budgetary participation and performance”, The International Journal of Accounting, vol. 43, pp. 268–292, 2008. |
| [8] | Huitema, B. E. The Analysis of Covariance and Alternatives. John Wiley & Sons, New York, 1980 |
| [9] | Mozaffar Khan, Ross L. Watts, “Estimation and empirical properties of a firm-year measure of accounting conservatism”, Journal of Accounting and Economics, vol. 48, pp. 132–150, 2009. |
| [10] | Syed Zulfiqar Ali Shah, Andrew W. Stark, Saeed Akbar, “The value relevance of major media advertising expenditures: Some U.K. Evidence”, The International Journal of Accounting, vol. 44, pp.187–206, 2009 |

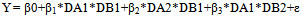
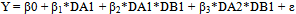
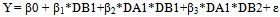
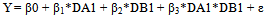
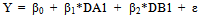
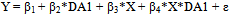
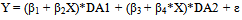
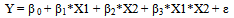
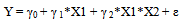
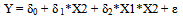
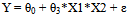
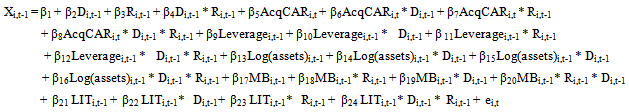
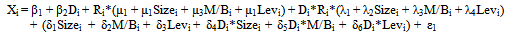
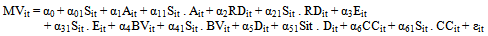
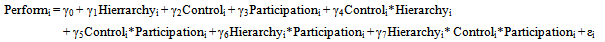
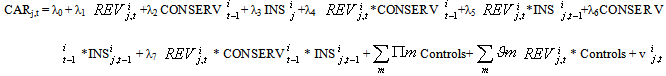
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML


