-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Finance and Accounting
p-ISSN: 2168-4812 e-ISSN: 2168-4820
2012; 1(3): 23-27
doi:10.5923/j.ijfa.20120103.01
Good Prediction of Gas Price between MLFF and GMDH Neural Network
Vida Varahrami
Kargar-e-Shomali Avenue, Faculty of Economics, University of Tehran, Tehran, Iran
Correspondence to: Vida Varahrami, Kargar-e-Shomali Avenue, Faculty of Economics, University of Tehran, Tehran, Iran.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Studies show neural networks have better results in predicting of financial time series in comparison to any linear or non-linear functional form to model the price movement. Neural networks have the advantage of simulating the non-linear models when little a priori knowledge of the structure of problem domains exist or the number of immeasurable input variables are great and system has a chaotic characteristics. Among different methods, MLFF neural network with back-propagation learning algorithm and GMDH neural network with genetic learning algorithms are used to predict gas price of the Henry Hob database covering 01/01/2004-13/7/2009 period. This paper uses moving average crossover inputs and the results confirms (1) the fact there is short-term dependence in gas price movements, (2) the EMA moving average has better result and also (3) by means of the GMDH neural networks, prediction accuracy in comparison to MLFF neural networks, can be improved.
Keywords: Artificial Neural Networks (ANN), Multi Layered Feed Forward (MLFF), Group Method of Data Handling (GMDH)
Cite this paper: Vida Varahrami, Good Prediction of Gas Price between MLFF and GMDH Neural Network, International Journal of Finance and Accounting , Vol. 1 No. 3, 2012, pp. 23-27. doi: 10.5923/j.ijfa.20120103.01.
Article Outline
1. Introduction
- Neural networks are a class of generalized nonlinear models inspired by studies of the human brain. Their main advantage is that they can approximate any nonlinear function to an arbitrary degree of accuracy with a suitable number of hidden units. Neural networks get their intelligence from learning process, and then this intelligence makes them have the capability of auto-adaptability, association and memory to perform certain tasks. The task of knowledge extraction from data is to select mathematical description from data. But the required knowledge for designing of mathematical models or architecture of neural networks is not at the command of the users In mathematical statistics it is need to have a priori information about the structure of the mathematical model. In neural networks the user estimates this structure by choosing the number of layers, and the number and transfer functions of nodes of a neural network. This requires not only knowledge about the theory of neural networks, but also knowledge of the object's nature and time. Besides this the knowledge from systems theory about the systems modelled is not applicable without transformation into an object in the neural network world. But the rules of translation are usually unknown[4].GMDH type neural networks can overcome these problems. It can pick out knowledge about object directly from data sampling. The GMDH is the inductive sorting-out method, which has advantages in the cases of rather complex objects, having no definite theory, particularly for the objects with fuzzy characteristics. GMDH algorithms found the only optimal model using full sorting-out of model-candidates and operation of evaluation of them, by external criteria of accuracy or difference types[1,2].In this paper, a method of non-parametric approach to predict the gold price over time in different condition of market is used. MLFF neural network with back-propagation algorithm and GMDH neural network with genetic algorithms are briefly discussed, and they are used to make appropriate model for predicting the gas price of Henry Hub Gulf Coast Natural gas spot price. As input variables to the neural networks, we use price time series separately with 2 lags of the 5, 10, 15, 30, 35, 50 and 55-day moving average crossover. These two models are coded and implemented in Matlab software package. The prime aim here is to find out dependence in gas price and also which neural network model does best in forecasting when the input parameters are little or great. The remainder of the paper is organized as follows. Section 2 describes the non-parametric modeling approach adopted here as per MLFF neural network with back-propagation algorithm and GMDH neural network with genetic algorithms which are briefly discussed. Section 3 discusses relevant concepts of the technical indicators used for the study. Empirical results are presented in Section 4 and concluding remarks in Section 5.
2. Modeling Using Neural Network
- Artificial Neural Networks (ANN) is biologically inspired network based on the organization of neurons and decision making process in the human brain[1]. In other words, it is the mathematical analogue of the human nervous system. This can be used for prediction, pattern recognition and pattern classification purposes. It has been proved by several authors that ANN can be of great used when the associated system is so complex that the underline processes or relationship are not completely understandable or display chaotic properties[13]. Development of ANN model for any system involves three important issues: (i) topology of the network, (ii) a proper training algorithm and (iii) transfer function. Basically an ANN involves an input layer and an output layer connected through one or more hidden layers. The network learns by adjusting the inter connections between the layers. When the learning or training procedure is completed, a suitable output is produced at the output layer. The learning procedure may be supervised or unsupervised. In prediction problem supervised learning is adopted where a desired output is assigned to network before hand[14].
2.1. MLFF Neural Network
- MLFF neural network is one the famous and it is used at more than 50 percent of researches that are doing in economy field recently[23]. This class of networks consists of multiple layers of computational units, usually interconnected in a feed-forward way. Each neuron in one layer has directed connections to the neurons of the subsequent layer. In many applications the units of these networks apply a sigmoid function as a transfer function (
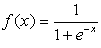 ). It has a continuous derivative, which allows it to be used in back- propagation. This function is also preferred because its derivative is easily calculated:
). It has a continuous derivative, which allows it to be used in back- propagation. This function is also preferred because its derivative is easily calculated: 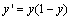 Multi-layer networks use a variety of learning techniques; the most popular is back-propagation algorithm (BPA). The BPA is a supervised learning algorithm that aims at reducing overall system error to a minimum[1,9]. This algorithm has made multilayer neural networks suitable for various prediction problems. In this learning procedure, an initial weight vectors
Multi-layer networks use a variety of learning techniques; the most popular is back-propagation algorithm (BPA). The BPA is a supervised learning algorithm that aims at reducing overall system error to a minimum[1,9]. This algorithm has made multilayer neural networks suitable for various prediction problems. In this learning procedure, an initial weight vectors 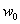 is updated according to[10]:
is updated according to[10]: 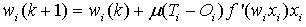 | (1) |
 The weight matrix associated with ith neuron;
The weight matrix associated with ith neuron;  Input of the ith neuron;
Input of the ith neuron; 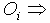 Actual output of the ith neuron;
Actual output of the ith neuron; 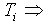 Target output of the ith neuron, and μ is the learning rate parameter.Here the output values (
Target output of the ith neuron, and μ is the learning rate parameter.Here the output values (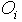 ) are compared with the correct answer to compute the value of some predefined error- function. The neural network is learned with the weight update equation (1) to minimize the mean squared error given by[10]:
) are compared with the correct answer to compute the value of some predefined error- function. The neural network is learned with the weight update equation (1) to minimize the mean squared error given by[10]: 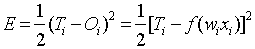 By various techniques the error is then fed back through the network. Using this information, the algorithm adjusts the weights of each connection in order to reduce the value of the error function by some small amount. After repeating this process for a sufficiently large number of training cycles the network will usually converge to some state where the error of the calculations is small. In this case one says that the network has learned a certain target function. To adjust weights properly one applies a general method for non-linear optimization that is called gradient descent. For this, the derivative of the error function with respect to the network weights is calculated and the weights are then changed such that the error decreases[18].The gradient descent back-propagation learning algorithm is based on minimizing the mean square error. An alternate approach to gradient descent is the exponentiated gradient descent algorithm which minimizes the relative entropy[19].
By various techniques the error is then fed back through the network. Using this information, the algorithm adjusts the weights of each connection in order to reduce the value of the error function by some small amount. After repeating this process for a sufficiently large number of training cycles the network will usually converge to some state where the error of the calculations is small. In this case one says that the network has learned a certain target function. To adjust weights properly one applies a general method for non-linear optimization that is called gradient descent. For this, the derivative of the error function with respect to the network weights is calculated and the weights are then changed such that the error decreases[18].The gradient descent back-propagation learning algorithm is based on minimizing the mean square error. An alternate approach to gradient descent is the exponentiated gradient descent algorithm which minimizes the relative entropy[19].2.2. GMDH Neural Network
- By means of GMDH algorithm a model can be represented as sets of neurons in which different pairs of them in each layer are connected through a quadratic polynomial and thus produce new neurons in the next layer. Such representation can be used in modeling to map inputs to outputs[1,2, 12]. The formal definition of the identification problem is to find a function
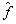 so that can be approximately used instead of actual one,
so that can be approximately used instead of actual one, 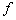 , in order to predict output
, in order to predict output 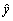 for a given input vector
for a given input vector 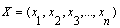 as close as possible to its actual output
as close as possible to its actual output 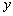 [22]. Therefore, given M observation of multi-input-single-output data pairs so that
[22]. Therefore, given M observation of multi-input-single-output data pairs so that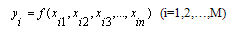 it is now possible to train a GMDH-type neural network to predict the output values
it is now possible to train a GMDH-type neural network to predict the output values 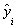 for any given input vector
for any given input vector 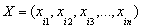 , that is
, that is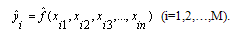 The problem is now to determine a GMDH-type neural network so that the square of difference between the actual output and the predicted one is minimized, that is
The problem is now to determine a GMDH-type neural network so that the square of difference between the actual output and the predicted one is minimized, that is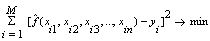 .General connection between inputs and output variables can be expressed by a complicated discrete form of the Volterra functional series in the form of
.General connection between inputs and output variables can be expressed by a complicated discrete form of the Volterra functional series in the form of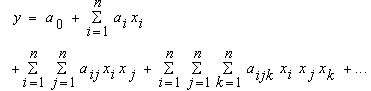 | (2) |
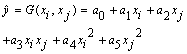 | (3) |
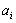 in equation (3) are calculated using regression techniques so that the difference between actual output, y, and the calculated one,
in equation (3) are calculated using regression techniques so that the difference between actual output, y, and the calculated one, 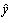 , for each pair of
, for each pair of 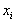 ,
, 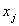 as input variables is minimized. Indeed, it can be seen that a tree of polynomials is constructed using the quadratic form given in equation (3) whose coefficients are obtained in a least-squares sense. In this way, the coefficients of each quadratic function
as input variables is minimized. Indeed, it can be seen that a tree of polynomials is constructed using the quadratic form given in equation (3) whose coefficients are obtained in a least-squares sense. In this way, the coefficients of each quadratic function 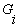 are obtained to optimally fit the output in the whole set of input-output data pair, that is[16]
are obtained to optimally fit the output in the whole set of input-output data pair, that is[16]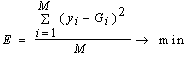 | (4) |
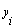 , i=1, 2, …, M) in a least-squares sense. Consequently,
, i=1, 2, …, M) in a least-squares sense. Consequently, 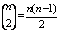 neurons will be built up in the first hidden layer of the feed forward network from the observations {
neurons will be built up in the first hidden layer of the feed forward network from the observations {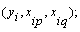 (i=1, 2,… M)} for different
(i=1, 2,… M)} for different 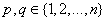 . In other words, it is now possible to construct M data triples {
. In other words, it is now possible to construct M data triples {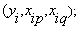 (i=1, 2,…, M)} from observation using such
(i=1, 2,…, M)} from observation using such 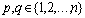 in the form
in the form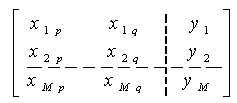 .Using the quadratic sub-expression in the form of equation (3) for each row of M data triples, the following matrix equation can be readily obtained as
.Using the quadratic sub-expression in the form of equation (3) for each row of M data triples, the following matrix equation can be readily obtained as 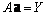 where
where 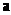 is the vector of unknown coefficients of the quadratic polynomial in equation (3)
is the vector of unknown coefficients of the quadratic polynomial in equation (3)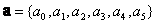 | (5) |
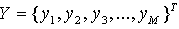 is the vector of output’s value from observation. It can be readily seen that
is the vector of output’s value from observation. It can be readily seen that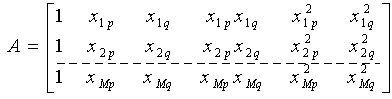 The least-squares technique from multiple-regression analysis leads to the solution of the normal equations in the form of
The least-squares technique from multiple-regression analysis leads to the solution of the normal equations in the form of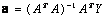 | (6) |
3. Technical Indicators Used for the Study
3.1. Simple Moving Average (SMA)
- This is perhaps the oldest and the most widely used technical indicator. It shows the average value of price over time. A simple moving average with the time period n is calculated by:
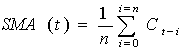 where Ct is a price at time t[17]. The shorter the time period, the more reactionary a moving average becomes. A typical short term moving average ranges from 5 to 25 days, an intermediate-term from 5 to 100, and long-term 100 to 250 days. In our experiment, the window of the time interval n is 5.
where Ct is a price at time t[17]. The shorter the time period, the more reactionary a moving average becomes. A typical short term moving average ranges from 5 to 25 days, an intermediate-term from 5 to 100, and long-term 100 to 250 days. In our experiment, the window of the time interval n is 5.3.2. Exponential Moving Average (EMA)
- An exponential moving average gives more weight to recent prices, and is calculated by applying a percentage of today's closing price to yesterday's moving average. The equation for n time period is[17]:
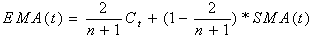 The longer the period of the exponential moving average, the less total weight is applied to the most recent price. The advantage to an exponential average is its ability to pick up on price changes more. In our experiment, the window of the time interval n is 5.
The longer the period of the exponential moving average, the less total weight is applied to the most recent price. The advantage to an exponential average is its ability to pick up on price changes more. In our experiment, the window of the time interval n is 5.4. Empirical Results
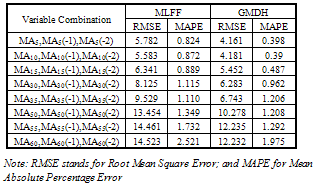
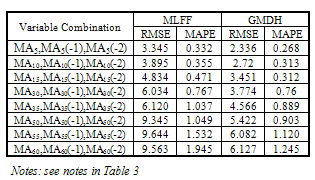
- As input variables to the neural networks, we use price time series covering 01/01/2004-13/7/2009 period separately, with 2 lags of the 5-day [MA5, MA5(-1), MA5(-2)], 10-day [MA10, MA10(-1), MA10(-2)], 15-day [MA15, MA15(-1), MA15(-2)], 30-day [MA30, MA30(-1), MA30(-2)], 35-day [MA35, MA35(-1), MA35(-2)], 50-day [MA50, MA50(-1), MA50(-2)], 55-day [MA55, MA55(-1), MA55(-2)] and 60-day [MA60, MA60(-1), MA60(-2)] moving average crossover. 5, 10 and 15-day simple moving average and EMA are used to measure the short-term dependency, 30,35 and 40-day moving average for intermediate-term dependency and 50, 55 and 60-day moving average are used to measure the long-term dependency in gas price. Training set is determined to include about 50% of the data set and the 25% will be used for testing and 25% for validating purposes. During the designing of MLFF model we have changed the number of layers and neurons. Finally we found the best network in this research as a network with 3 hidden layers and 15-8-10 neurons. Almost 100 transfer function has been used and sigmoid is used for the input function and the linear function is used for output. Table 1 summarizes the characteristics of the best network.
|
|
|
|
5. Conclusions
- Gas is an important traded commodity and forecasting its price, has important implications economically. Despite the significant number of studies on gas and its price, the precise pricing mechanism in the gas market has not been deciphered. Many of them are based on neural network and it shows they are much better than the other methods. This paper used two types of neural networks to investigate the price of gas. It has been shown that GMDH type neural networks have better results when the associated system is so complex and the underline processes or relationship are not completely understandable or display chaotic properties.We have used gas price time series and its moving average as the input to the neural network and the results show:1- The GMDH has better response relative to MLFF neural network.2- Gas price has short-term dependence to its history.3- The exponential moving average is a better choice relative to simple moving average, if the moving average techniques are used.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML