1. Introduction

The revealed limits of fossil fuels, the threat posed by global warming and the ever-increasing need for global energy have prompted exploration of other so-called renewable energy sources, including solar energy. Considered to be the world’s oldest energy, on which almost all other energy sources depend, it is used either directly or after transformation into other forms of energy (thermal energy, electric energy).

The central element of the solar thermal energy applications is the solar thermal collector. It transforms the radiant energy of the sun into thermal energy extracted by the flowing fluid. This energy is used in various applications such as drying, domestic and industrial heating, solar cooling production, etc. [1]. Most of the research is being devoted to the development of solar collectors using water as heat transfer fluid in terms of thermal efficiency. In general, there are few studies on solar collectors using air as heat transfer fluid because, air does not have a better heat exchange efficiency due to its low thermo-physical properties [2]. However, with the current technological development, this field has undergone significant renewal in theory and experiment [2-6]. Thus, several scientific studies have been carried out on these collectors, with the aim of optimizing the useful energy transmitted to air, by acting on the optical (relating to transparent covers) and geometric (shapes and dimensions) properties of the collector, as well as all other parameters that may affect its thermal performance [7-10].

Transparent cover in a collector has the dual function of allowing the maximum amount of solar radiation to pass and avoiding the cooling of the absorber, reducing air convection phenomena and "blocking" emitted infrared radiation [11,12]. Such a device thus represents a real trap to solar radiation, which can be improved by equipping the collector with an additional cover (double cover) or by playing on the properties of the material of the cover [13-14]. It then realizes greenhouse effect, which involves both solar radiation and infrared radiation.

Important studies have been carried out in the context of the optimization of flat-sided solar air collectors [15]. In particular, there is an important bibliography on exchange modelling in collectors [16-19] but so far, it has only been concerned with macroscopic phenomena and has only been concerned with sensors whose transparent cover whether simple, double or triple glazing is always flat. Also, in all this work the influence of infrared radiation (greenhouse effect) has always been mentioned superficially. Although mathematical modelling of infrared thermal radiation inside the greenhouse has been developed [20,21], such work with regard to solar air collectors are quite rare.

A new solar collector with W-shaped cover form was design and their thermal performance was experimentally characterized [22]. In this article, we have focused our attention on modelling and numerical simulation of the greenhouse effect of that new solar collector.

2. Material and Methods

2.1. Material and Physical Model

The Fig. 1 shows the W-shape geometry [22].

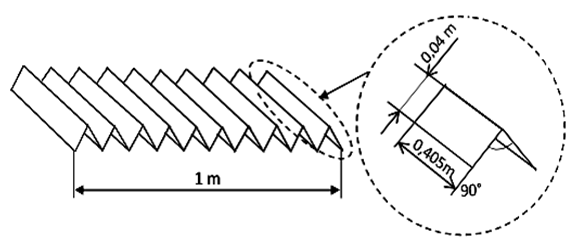Figure 1. Representation of the W-shape glass and the absorber form

In Fig. 2, we show the physical model of different configurations studied: flat plate solar collector, semi W-shape solar collector, W-shape solar collector.

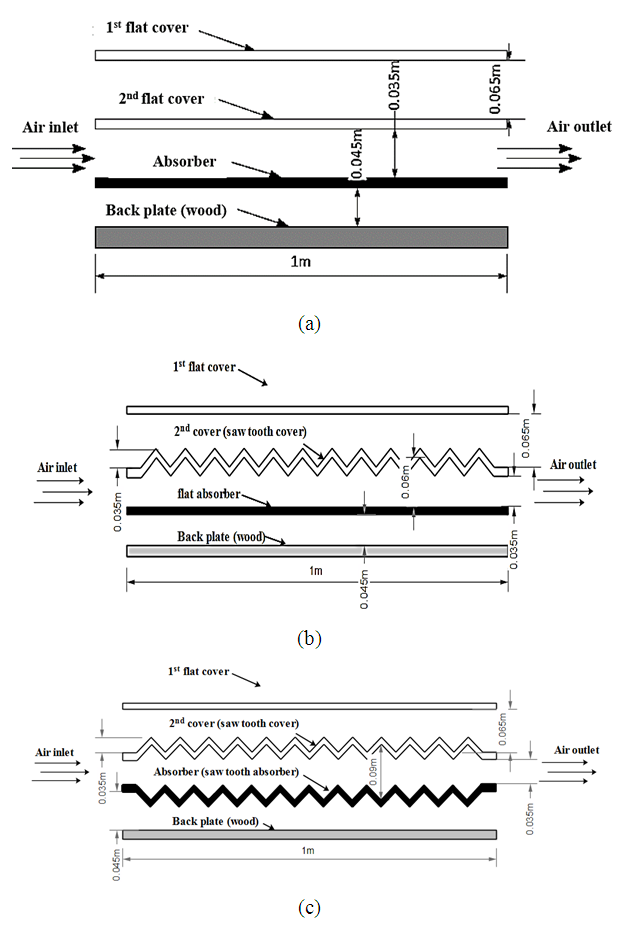Figure 2. Physical models: (a) flat plate solar collector, (b) semi W-shape solar collector, (c) W-shape solar collector

Greenhouse effect modelling in the solar collector

Radiation from the collector’s cover reaches the absorber directly or indirectly after an arbitrary number of reflections and/or transmissions through the glass surface and reflections by the absorber. Our objective is to take into account this multitude of radiation paths. Work has been carried out in that sense [21,21] but within the framework of an agricultural greenhouse, assuming throughout its work that the exchange of radiation takes place between completely diffusive surfaces, this means that all radiation emitted, reflected or transmitted has a uniform intensity in all angular directions. As regards to thermal radiation, we know that it is emitted isotropically by the radiant surface: this assumption is therefore valid in this case.

2.2. Concept of Multiple Reflections

2.2.1. Double-glazed Flat Solar Collector

The useful profile of a double-glazed flat collector can be assimilated to three parallel flat surfaces. What we are interested in are the radiation exchanges between the first glass 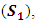the second glass 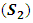and the absorber 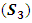as shown in Fig. 3. The rays can take a multitude of paths.

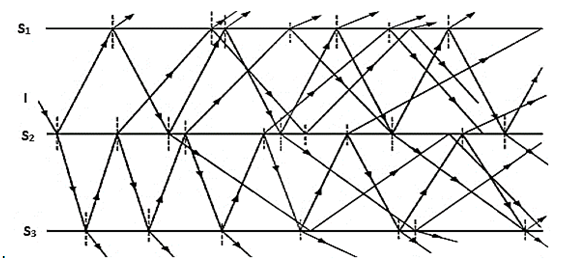Figure 3. Possible paths of radiation in the double-glazed flat solar collector

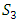In the particular case where is a diffuse emission grey surface, the amount of radiation actually absorbed may be determined [23,24]:

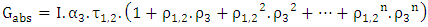(1)

with:

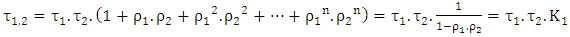(2)

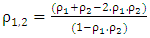(3)

The factor materializing the phenomenon of multiple reflections is given by:

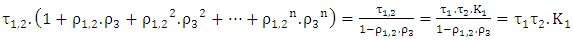(4)

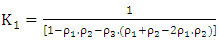(5)

2.2.2. Semi W-shape Collector

The semi W-shape collector can be assimilated to three surfaces exchanging radiation as shown in Fig. 4. What we are interested in are the radiation exchanges between the flat glass (S₁), the W-shape glass (S₂) and the absorber (S₃).

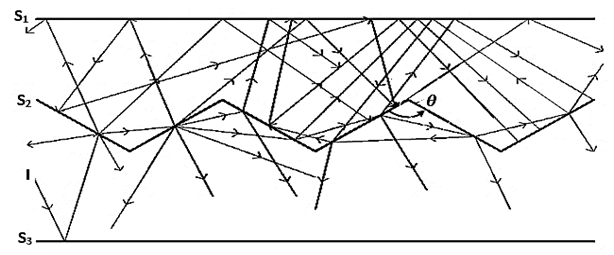Figure 4. Possible paths of radiation in the semi W-shape solar collector

We define angle factors as follows:

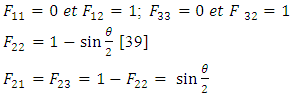Where θ is the angle of the W-shape sections.

In the particular case where (S₃) is a diffuse emission grey surface, the amount of radiation actually absorbed is given by equation (1).

For this configuration, 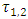is given by:

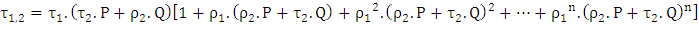(6)

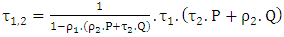(7)

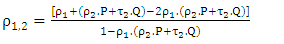(8)

In these relations, P represents the fraction of radiation from the underside of the W-shape (S2 surface) that finally reaches the S1 surface, directly or indirectly (after an arbitrary number of reflections and/or transmissions through different parts of the saw tooth); similarly, Q represents the fraction of radiation from the top side of the W-shape finally reaching the S1 surface after all possible radiation exchange paths between the tooth parts.

The factor materializing the phenomenon of multiple reflections is given by:

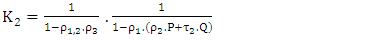(9)

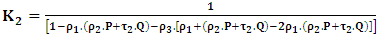(10)

2.2.3. W-shape Collector

The W-shape collector can be assimilated to three surfaces exchanging radiation as shown in Fig. 5. What we are interested in are the radiation exchanges between the flat glass (S₁), the W-shape glass (S₂) and the W-shape absorber (S₃).

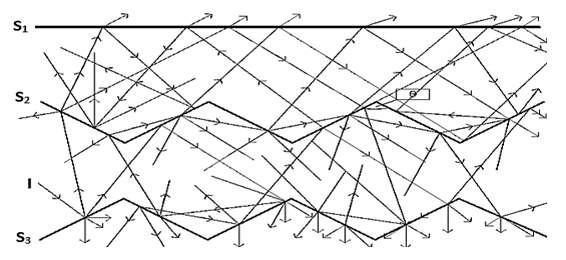Figure 5. Possible paths of radiation in the W-shape solar collector

We define angle factors as follows:

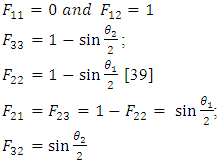Where 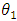and 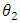are the angles formed by the W-shape sections of the second pane and the absorber respectively.

In the particular case where 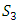is a diffuse emission grey surface, the amount of radiation actually absorbed is given by equation (1). 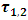and 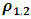are given by the equations (7) and (8).

The factor materializing the phenomenon of multiple reflections is given by:

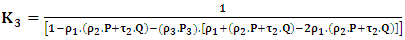(11)

P3 is defined in a similar way to

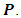
2.3. Net Infrared Radiation

2.3.1. Different fluxes

Tn is the absolute temperature of the surface n. Its emissive power, that is the rate of energy emitted per unit of surface, is given by the Stefan-Boltzmann law:

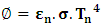(12)

Flux emitted by the atmosphere

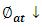Flux density descending from atmospheric radiation reaching the absorber is given by:

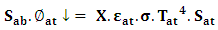(13)

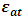It involves the factor which represents the infrared emittance of the sky, known to be somewhere between 0.72 (clear sky) and 1 (overcast sky) [25].

X takes into account collector configuration (angle factor, roofing transmission coefficients) and multiple reflections.

2.3.2. Flux Emitted by the Transparent Cover

Flux density descending from the thermal radiation emitted by the transparent cover 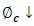which reaches the absorber is given by:

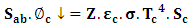(14)

Z takes into account the collector’s configuration (angle factor, roofing transmission coefficients) and multiple reflections.

2.3.3. Flux Emitted by the Absorber

The radiation emitted by the absorber also gives rise to a descending flux density 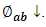It includes two contributions: the flux density of radiation emitted by the absorber which after reflection at first contact with the cover, is finally returned, and the corresponding flux density which is transmitted during its first contact with the cover but which is finally returned after a certain number of exchanges in different parts of the cover, while taking into account the multiple reflections.

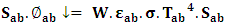(15)

W takes into account the collector’s configuration (angle factor, roofing transmission coefficients) and multiple reflections.

2.3.4. Absorbed Infrared Radiation

The radiation absorbed by the sensor is then simply deduced:

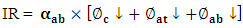(16)

2.4. IR radiation Losses

2.4.1. Different Fluxes

Ascending thermal radiation fluxes have the following flux densities:

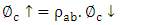(17)

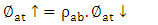(18)

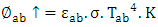(19)

2.4.2. Radiation Losses

The radiation losses by the absorber are deduced using equation (20):

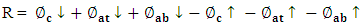(20)

3. Results and Discussion

3.1. Profil of Infrared Radiation

Infrared radiation absorbed by the double-glazed flat collector takes into consideration the following different fluxes

First cover:

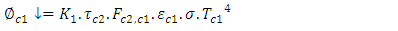(21)

Second cover:

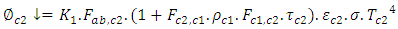(22)

Atmosphere:

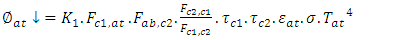(23)

Absorber:

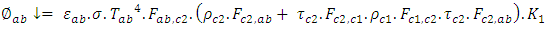(24)

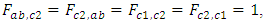Taking into consideration that in this flat collector, the amount of infrared radiation absorbed is given by the equation (25):

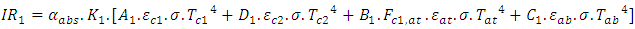(25)

with:

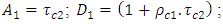
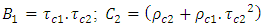Following the same reasoning, the amount of infrared radiation absorbed by the semi saw-teeth collector is given by the equation (26):

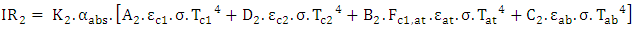(26)

With:

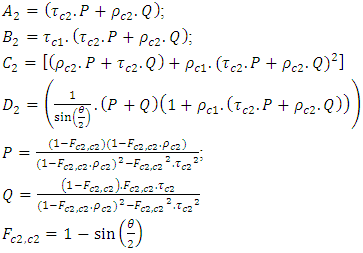The amount of infrared radiation absorbed by the saw-teeth collector is given by the equation (27):

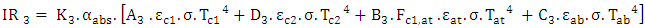(27)

With:

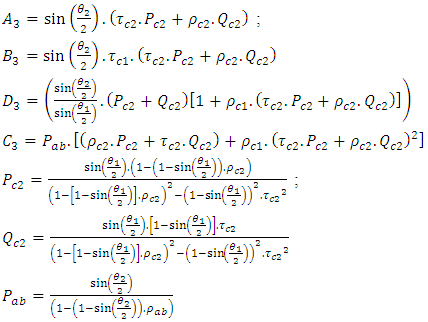The Fig. 6 shows the net absorbed IR radiation curves for the three double glazed sensor configurations. The graph also showed the evolution of solar radiation.

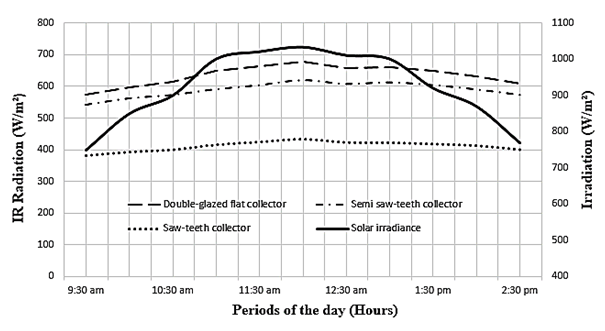Figure 6. Infrared Radiation absorbed by the collector

The IR radiation curves describe almost the same evolution as that of the solar density, they increase during the morning and decrease in the afternoon with the maximum IR radiation absorbed around 12:00 am (local time), which is justified. The double-glazed flat collector is the one that absorbs the most IR radiation with about 678 W.m^-2 at 12:00 am, and then comes the semi saw-teeth collector with about 620 W.m^-2 at the same time. 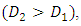This difference is due firstly to the temperatures of the sensor elements which are globally higher in the flat collector, and secondly to the saw tooth geometry of the second transparent cover for the semi saw-teeth collector, which accentuates the amount of IR radiation that the cover emits towards the absorber but nevertheless reduces the amount of radiation from the atmosphere 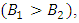the first cover 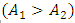and the amount emitted by the absorber that is returned to it 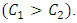The saw-teeth collector has the lowest amount of absorbed IR radiation, approximately 433.2 W.m^-2 at 12:00 am. This is due, in addition to the reasons listed above (temperature of the sensor elements and geometry of the second cover), to the geometry of the absorber. The saw tooth geometry of the absorber in this collector configuration significantly reduces the absorbed IR radiation.

3.2. Radiation Losses at the Absorber Level

The radiation losses at the level of absorber on double-glazed flat collector are given by the equation (28):

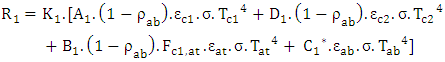(28)

with:

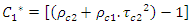The absorber radiation losses in case of the semi W-shape collector are given by expression (29):

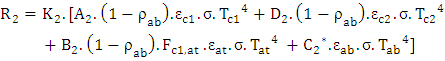(29)

with:

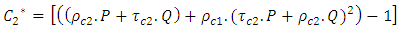The radiation losses at the level of absorber of W-shape collector are given by expression (30):

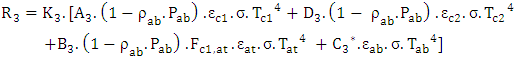(30)

with:

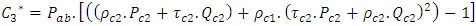In Fig. 7, we show the profiles of radiation losses for different configurations: double-glazed flat collector, semi W-shape collector and W-shape collector.

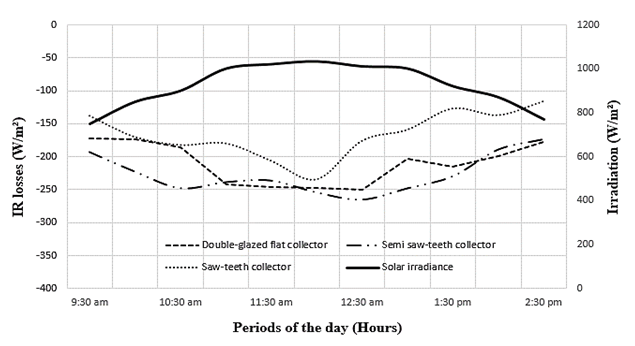Figure 7. IR radiation losses at the absorber for different configurations

The radiation loss curves all have a bathtub shape where the highest peak is observed at 12:00 am (local time) for the saw-teeth collector and 12:30 am (local time) for the other two collectors. Analysis of these curves shows that the radiation losses (difference between the amount of IR coming in and the amount leaving the absorber) are smaller in the saw-teeth collector (234.3 W.m^-2 at 12:00 am. This is due to the geometry of the absorber. The saw tooth shape reduces the amount of radiation that leaves the absorber and thus keeps it warm. When the absorber is flat, the radiation losses are greater (250 W.m^-2 and 265 W.m^-2 respectively for the double-glazed flat collector and the semi saw-teeth collector at 12:30 am).

3.3. Influences of Angle Factor

3.3.1. Case of the Semi W-shape Collector

Fig. 8 and 9 are obtained by varying the angle of the W-shape of collector. In Fig. 8, we show the absorbed IR radiation curves for different angle values, while in Fig. 9 the radiation losses (at the absorber level) for the same angle values.

Analysis of the curves shows that the angle value of the glazing tooth has an important effect on the absorbed IR radiation and on the losses of IR radiation in the semi saw-teeth collector. The Fig. 8 shows that absorbed IR radiation increases with the angle of the saw tooth. It is particularly important when the angle of the saw tooth is obtuse. For IR radiation losses (Fig. 9), they decrease when the tooth angle value increases. These results are consistent with those in the literature.

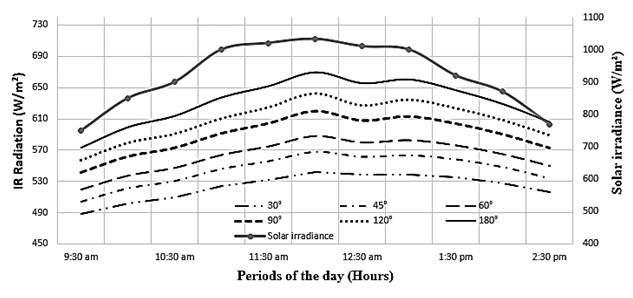Figure 8. IR radiation absorbed by the semi W-shape collector for different angle values of the W glass

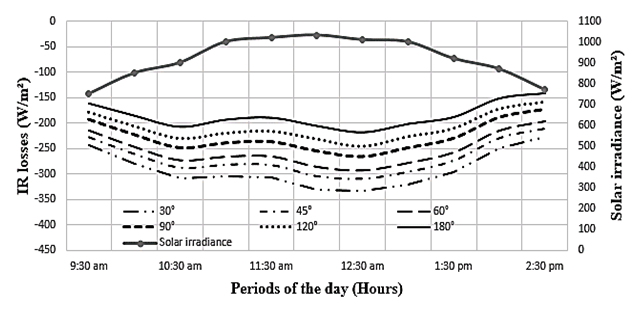Figure 9. Radiation losses at the absorber of the semi W-shape collector for different angle values of the W glass

3.3.2. Case of the W-shape Collector

3.3.2.1. Angle of W-shape Glass

Fig. 10 and 11 respectively represent the net absorbed IR radiation curves and the radiation loss curves in the W-shape collector for different angle values of the W of the transparent cover when the angle of the W absorber is fixed.

Analysis of the curves shows that, when the value of the angle of the absorber tooth is fixed, the variation in the glazing angle has a significant effect on the absorbed IR radiation and on the losses of IR radiation in the saw-teeth solar collector. The absorbed radiation increases with the angle of the glazing (Fig.10). With regard to radiation losses (Fig. 11), they decrease when the tooth angle value increases. However, the variations are not as large as for absorbed radiation.

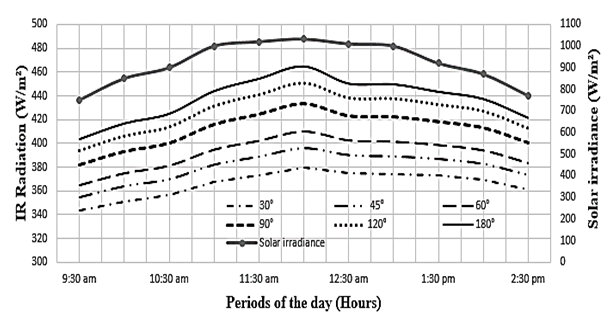Figure 10. IR radiation absorbed by W-shape collector for different angle values of the W-glass

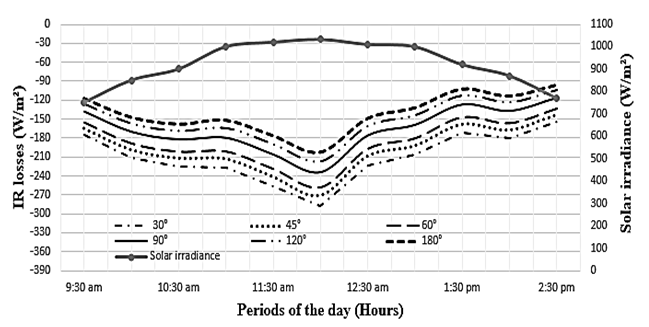Figure 11. Radiation losses of the W-shape collector for different angle values of the W glass

3.3.2.2. Angle of the W-shape Absorber

In Fig. 12 and 13 respectively, we represent the net absorbed IR radiation curves and the radiation loss curves in the W-shape collector for different angle values of W of the absorber when the angle of W of the transparent cover is fixed.

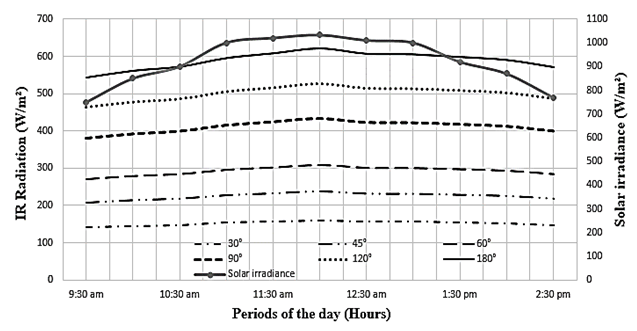Figure 12. IR radiation absorbed by the W-shape collector for different angle values of the W absorber

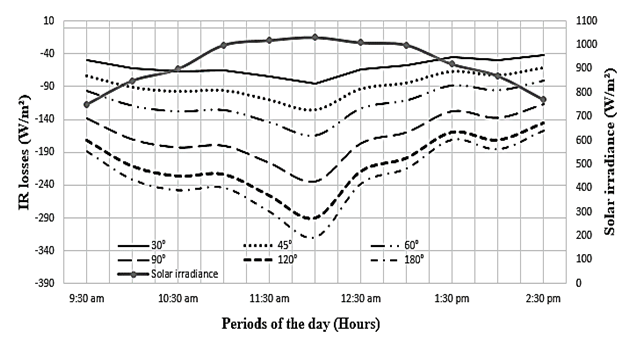Figure 13. Radiation losses of the collector for different angle values of the W absorber

Analysis of the curves shows that, when the value of the W-shape angle of the transparent cover is fixed, the angle of the absorber significantly influences the absorbed IR radiation as well as the radiation losses in the W-shape solar collector. By increasing the angle of the W of the absorber, we observe a significant increase in absorbed IR radiation (Fig. 12). We also see a significant increase in radiation losses (Fig. 13). In both cases, the higher the angle, the greater the influence of temperatures (period of day) on the curves.

4. Conclusions

In this article a mathematical model has been developed to calculate the net infrared radiation absorbed as well as the radiation losses at the absorber level for the semi W-shape and W-shape solar collectors. The results showed that the maximum values of the net absorbed radiation are reached at solar noon, when the solar radiation is maximum in the locality. The maximum loss value is also observed at solar noon for the W-shape solar collector but 30 minutes later for the other two solar collectors. This is due to the inertia of the flat absorbers (double-glazed flat solar collector and W-shape solar collector). From the comparative study, it is apparent that the W-shape solar collector absorbs the least amount of IR radiation (433.2 W.m-2) compared to the other two (678 W.m^-2 and 620 W.m^-2 respectively for the double-glazed flat and the semi W-shape solar collector). However, the analysis of the radiation losses at the absorber showed that it retains much more heat (234.3 W.m^-2 compared to 250 W.m^-2 and 265 W.m^-2 respectively for the double-glazed flat solar collector and the semi W-shape solar collector), and therefore transmits as much to the coolant. The variation in the angle factors of the transparent cover and absorber showed that, when the angle of the W of the cover increases, the absorbed IR radiation also increases, while the losses of radiation to the absorber decrease; when the angle of the W of the absorber increases (W-shape solar collector), the amount of IR radiation absorbed and the losses of IR radiation to the absorber also increase.

5. Nomenclature