1. Introduction

The problem of food loss, though a global one, is particularly significant in developing countries where food losses are estimated to be of the order of 40%, but can rise to be as high as 80% under very adverse conditions. A significant percentage of these losses is related to improper and, or untimely drying of foodstuffs such as cereal grains, meat, tubers and fish [1]. One reason for loss of grain after harvesting is spoilage resulting from high moisture content. Postharvest loss of maize in Kenya in 2007 was 21.1% [2]. Drying of the grain is necessary to avoid loss between harvesting and consumption. High moisture content encourages loss due to attacks by insects, pests and increased respiration. This is in addition to fungus infection, which renders it unusable [3, 4]. According to [3, 5], drying of crop helps to achieve better product quality, longer safe storage and reduction of post-harvest loss hence ensuring more food is available for the growing world population. Also, drying using solar energy leads to conservation of conventional energy sources.

Various researchers have evaluated the performance of solar dryers on the basis of different criteria. [6], use dryer thermal efficiency, drying rate and specific moisture extraction rate as their basis, while [7] base their evaluation solely on dryer efficiency. Uniformity of drying in different trays, and even within the same tray, is also important in evaluating dryer performance [8]. This research focused on drying rate as performance criteria.

When a kernel of grain dries, two processes occur simultaneously: transfer of heat from the air to the kernel to evaporate water and transfer of mass as internal liquid and vapour move from kernel to air. Several theories have been advanced to explain movement of moisture within the kernel. All may occur simultaneously, but one may be predominant at any one time. Also, different ones may be predominant at different times. The diffusion theory relies on Fick’s law [eq. (1)] to explain liquid diffusion within the kernel. In this equation, P is the rate of permeation while k, A and 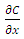represent diffusion constant, cross sectional area and concentration gradient respectively [9].

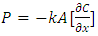(1)

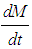Drying rate is given by eq. (2) [4], 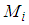and 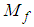being initial and final moisture fractions, respectively.

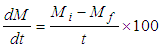(2)

However, drying rate varies every instant and would not be beneficial to the user, in planning drying schedules, for example. This research therefore adopted moisture removal rate (ratio of mass of moisture removed to mass of wet grain per hour) as this would then be used to predict the total drying time for some given quantity of product with certain moisture content.

Factors affecting drying rate include air temperature, air velocity, porosity of product, layer thickness and moisture content of product. Other factors are humidity of the surrounding air, method of drying, moisture diffusivity and drying kiln structure [1, 4, 10].

Researchers have investigated effect of various parameters on the drying of products such as longan, bananas, yam, beans, maize, mango and cassava using forced convection dryers. Drying air temperature in most of these studies ranged between 40°C and 60°C [11-13]. [14] used a wider temperature range of 35.2°C – 69.8°C. In the current study, a lower limit of 40°C was used to ensure drying air temperature was always greater than the ambient, while an upper limit of 60°C was used to avoid cracking and discoloration of the grain. Air velocities in most studies ranged from 0.22 m/s to 2 m/s [15-20]. In this research, the air velocity range applied was 0.212 m/s – 0.408 m/s. Very low air velocities would have resulted in very high drying air temperatures, while high velocities would lead to low air temperatures. Also [10] reported that air velocities above 0.42 m/s have no influence on drying rates.

A forced convection solar grain dryer requires adequate air flow in order for the drying process to occur effectively. This requires the use of an appropriate fan, one that will overcome the static pressure developed in the drying cabinet, and also ensure air flow at the appropriate velocity. [8] reported that optimum air flow rate is essential for achieving satisfactory dryer performance. Slower air flow rate may increase drying air temperature while higher air flow rate may decrease moisture removed.

Studies on dry basil leaves, orange peels and carrots showed that drying rate was directly proportional to drying air velocity [10, 18, 20-22]. [14] is in agreement and attributes this to interaction of a large volume of air with the drying product. However, air flow rates above 6000kg/m²hr had no influence on drying rate [10, 23]. This is equivalent to an air velocity of 0.42 m/s and influenced the decision on the highest air velocity used in this research. [24], however, after investigations of banana, reported that 1 m/s drying air velocity resulted in best quality in terms of colour, taste and shape in comparison to 0.5 and 2 m/s.

The grain layer thickness should not be too big to prevent penetration by the hot air, neither should it be too small to prevent efficient utilization of the available thermal energy. [25] carried out experiments to analyse drying behavior of potato at a constant air velocity of 0.6 m/s, temperatures of 40, 45 and 60°C, and product thicknesses of 3 mm, 5 mm and 7 mm. It was found that drying time increased with increase in thickness, thus implying that drying rate was greater for thinner layers. [21, 26] reported similar results after studies on orange peels. In this research, effect of grain layer thickness on moisture removal rate was investigated.

The product being dried is generally placed in trays during the application of a solar dryer. This, however, results in uneven drying due to poor air flow distribution. [27] used Computer Fluid Dynamics Simulation and experiments to investigate air flow distribution in the drying chamber. They also found that decreased air velocity resulted in reduced drying rate. Thus, the moisture content differed from one tray to another, the lowest being in the tray closest to the air inlet. The current study, however sought to determine whether use of more than one tray significantly affects the performance of a dryer. [28] found that when many trays are used, drying rate decreases as distance from the air inlet increases. [14], reported that drying air temperature in the drying cabinet decreased with height, resulting in lowest air temperature and highest moisture content at the top-most parts of the shelf.

Using an indirect forced convection solar dryer to study thin layer drying of prickly pear peels, [12] carried out experiments at 50-60°C drying air temperature and 0.0277-0.0833 m³/s drying air flow rate. The main factor controlling drying rate was found to be drying air temperature. [26] concurred. Researchers such as [20-23, 25, 29] as well as [20], among others, showed that drying rate is proportional to drying air temperature. These conclusions emanated from investigations involving products such as thymus and mint.

2. Materials and Methods

The experimental solar grain dryer (Figures 1 and 2 consisted of a flat plate solar collector (air heater) and a drying cabinet with a centrifugal fan to force the air into the dryer. The solar collector area was 1.2 m x 1.8 m, and the air vent was of height 0.1 m. The absorber plate comprised of black painted corrugated iron sheet. The glass cover was of 5 mm thick glass, the air heater sides and back plate being made of 5 mm thick ply wood. The drying chamber was of dimensions 0.5 m x 0.5 m x 1 m, with a 1.25 mm MS sheet metal casing. Its sides consisted of double plates, 40 mm apart with polystyrene in between for lagging. A centrifugal fan was fixed at the upper section of one side. The plenum chamber was covered with a perforated plate 0.2 m from the bottom of the drying cabinet. Two drying trays, whose sides were of 1.25 mm MS sheet metal, with bottoms of wire mesh, were used. The first was 0.1 m above the perforated plate, and the second 0.2 m from the bottom of the first.

Figure 1. Side View of Experimental Solar Grain Dryer

Figure 2. Rear View of Experimental Solar Grain Dryer

2.1. Determination of Moisture Removal Rate

To determine moisture removal rate (R_mr), moisture loss in each drying session was calculated from the difference between the mass of grain before and after drying, weighed using a digital balance. R_mr was determined using eq. (3), and was defined as the mass of moisture m_m, lost during a drying session of time t for every unit mass of wet grain m_w.

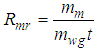(3)

2.1.1. Effect of Air Velocity

To determine effect of air velocity on moisture removal rate, the dryer was tested at air velocities of 6.8 m/s, 8.6 m/s, 11 m/s and 13 m/s, measured at the dryer exit using a thermo-anemometer. A grain layer thickness of 0.02 m was used in each case, the dryer being ran for 3 ½ hours. Using eq. (4), the equivalent air velocities within the drying cabinet, of cross sectional area 0.5 x 0.5 m, were 0.212 m/s, 0.272 m/s, 0.344 m/s and 0.408 m/s respectively.

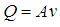(4)

2.1.2. Effect of Grain Layer Thickness

To determine effect of grain layer thickness on moisture removal rate, the dryer was tested at air velocities 0.212 m/s and a grain layer thickness of 0.02 m, using a procedure similar to section 2.1.1. This procedure was repeated for 0.04 m, 0.06 m and 0.08 m thick layers.

2.1.3. Effect of Number of Trays

The solar dryer was tested to determine whether its performance would be affected by the use of more than one drying tray. First, a 0.04 m thick grain layer was dried in one tray using an air velocity of 0.408 m/s, and the moisture removal rate determined. The experiment was repeated, using two trays each with 0.02 m thick grain layer at the same air velocity, again determining the moisture removal rate, which was compared to the result for a single tray. This procedure was repeated for an air velocity of 0.212 m/s.

2.1.4. Effect of Drying Air Temperature

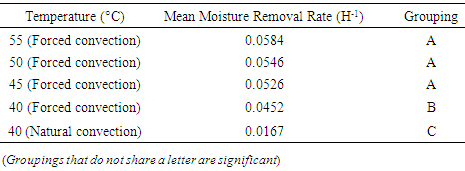
To determine the effect of temperature on dryer performance, experiments were done under laboratory conditions, where drying air temperature was controlled. A 1.8 kW heating coil, connected to a Proportional Integral Derivative (PID) controller was used to heat air to the required temperature. Temperature was measured using J-type thermocouples. First, a 0.02 m grain layer thickness was dried at an exit air velocity of 0.408 m/s and 40°C, determining the moisture removal rate. Samples of the grain were retrieved every 30 minutes for 3 ½ hours. This was repeated at 45°C, 50°C and 55°C, maintaining the same grain layer thickness and exit air velocity in order to observe the effect of temperature on the MRR. Variation of MRR with temperature was analysed using ANOVA and LSD. As a control, the same experiment was repeated for the same grain layer thickness but with natural convection at 40°C and the performance compared to that of forced convection (0.408 m/s).

3. Results and Discussion

3.1. Effect of Selected Parameters on Performance of Experimental Dryer

3.1.1. Effect of Air Velocity

Variation of moisture removal rate (MRR) with air velocity for given grain layer thicknesses are presented in fig. 3. It is notable that MRR generally increased with increase in air velocity for a given grain layer thickness. This is because at greater velocity, the air was able to carry away more moisture. [18, 20, 21]. [25, 26] reported similar results, although theirs were with respect to drying rate, a criteria similar to moisture removal rate. The highest MRR for 0.02 m grain layer thickness was 0.061 kg moisture/ (kg wet grain. hour) at 0.408 m/s air velocity, while the lowest was 0.048 kg moisture/ (kg wet grain. hour) at 0.212 m/s. It is, however, evident that for 0.04 m, 0.06 m and 0.08 m grain layer thicknesses, there is a slight decrease in MRR from 0.212 m/s to 0.272 m/s. This could have been due to a decline in temperature, which was not controlled during the experiment.

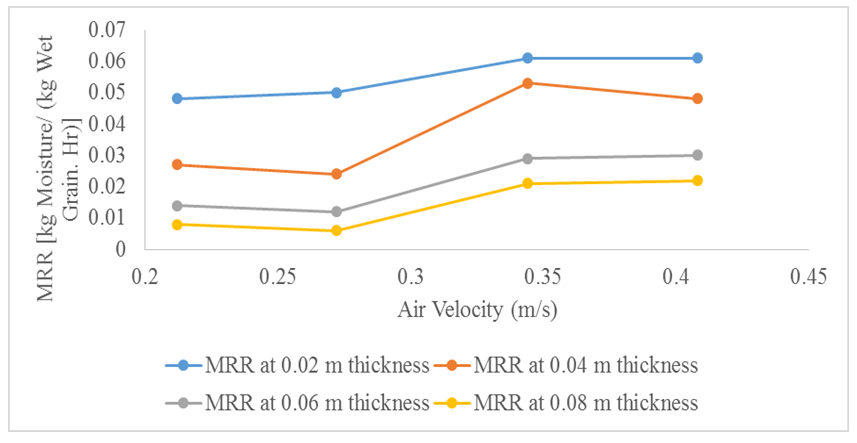Figure 3. Moisture Removal Rate vs. Air Velocity

3.1.2. Effect of Grain Layer Thickness

Fig. 4 shows how moisture removal rate varied with grain layer thickness at constant air velocity. It may be seen that for any given air velocity, moisture removal rate decreased as the grain layer thickness increased. These results are similar to those of [25, 26]. The possible explanation is that as grain layer thickness increased, the air absorbed more and more moisture as it was rising up. It thus became more humid resulting in a decline in its capacity to remove more moisture. Also, applying Fick’s law [(eq. (1)], the rate of permeation was lower for a greater layer thickness since the quantity 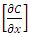decreased, as the denominator (thickness) increased in spite of the numerator (concentration) remaining unchanged. It was also noted that the moisture removal rates at 0.212 m/s and 0.272 m/s on one hand, and for 0.344 m/s and 0.408 m/s on the other, were very close. This was probably because the intervals for air velocities were not uniform, that between 0.272 m/s and 0.344 m/s, for example being greater than that between 0.212 m/s and 0.272 m/s.

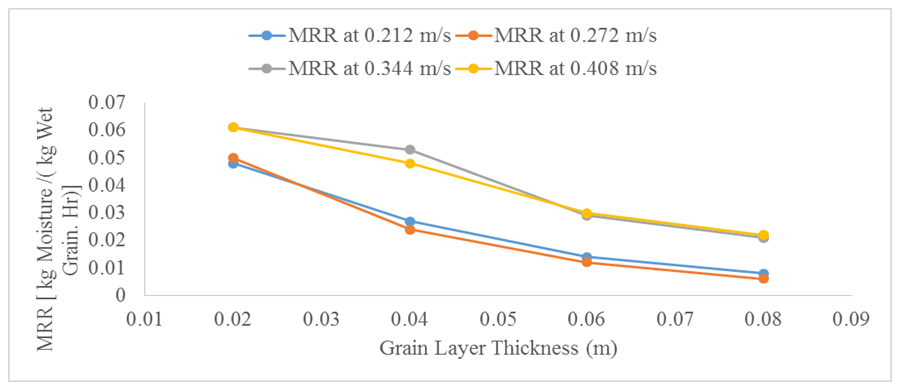Figure 4. Moisture Removal Rate vs. Grain Layer Thickness

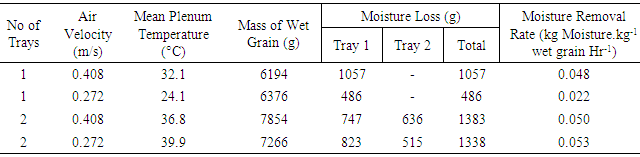
3.1.3. Effect of Number of Trays

Table 1 is a comparison of the MRR of the dryer when 0.04 m grain layer thickness was dried as a single layer in one tray on one hand, and as two single layers of 0.02 m each in two trays, on the other. The mean drying temperatures also changed since the maize was dried on different days.

Table 1. Dryer Performance for One and Two Trays

ANOVA was carried out to determine whether drying 0.04 m grain layer thickness as a single layer in one tray, or in two 0.02 m layers in two trays would have any significant effect on the MRR of the dryer if air velocity and drying air temperature were constant. The results for air velocity of 0.408 m/s showed the existence of no significant difference (P>0.05; F_comp = 1.008; F_{Crit. 5%} = 19.000) for the effect of changing number of trays on moisture removal rate (Appendix VI E). This is in spite of air temperature rising from 32.1°C for a single tray to 36.8°C for two trays. Thus there would be no significant benefits in using more than one tray in the dryer. This is because the hot air acquires no extra capacity to remove air even if extra trays are used. Indeed, it is evident that where two trays are used, then moisture removal rate is greater in the first tray. This is in agreement with findings reported by [28] after studies on drying of mint. The situation where an air velocity of 0.272 m/s was used (for one and two trays) was difficult to compare since drying air temperature increased by 15.8°C, probably explaining the significant increase in MRR from 0.022 kg Moisture.kg^-1 wet grain Hr^-1 for one tray, to 0.053 kg Moisture.kg^-1 wet grain Hr^-1 for two trays.

3.1.4. Effect of Temperature

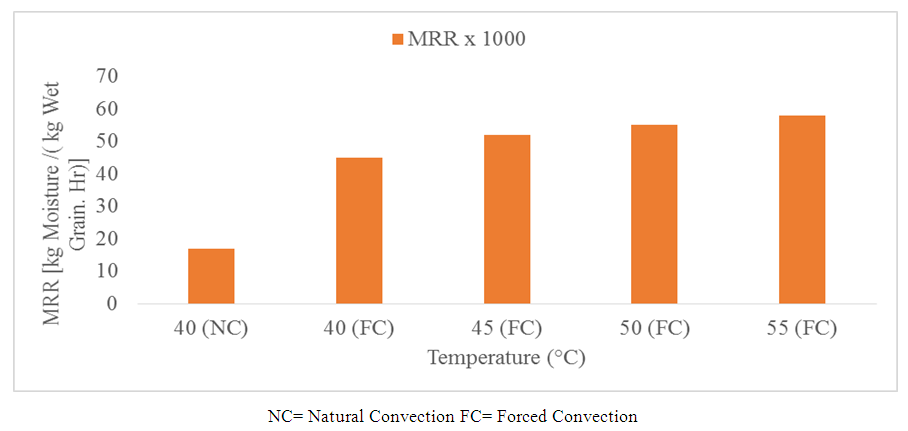
Fig. 5 shows the variation of dryer performance with Moisture removal rate, which, increased with drying air temperature, and was also lower for natural convection than forced convection. [20, 21, 23], reported similar results, though with respect to drying rate. MRR is a measure of drying rate and is expected to vary in a similar manner.

Figure 5. Effect of Temperature on Moisture Removal rate

One way ANOVA was carried out to determine whether the effect of temperature on dryer efficiency was significant. Using the Tukey method for information grouping (95% Confidence Level), it was found that increasing temperature between 40 to 45°C, 45 to 50°C and 50 to 55°C in each case had a significant effect on dryer efficiency, which was reduced, during forced convection drying. There was also a significant difference in dryer efficiency between drying at 40°C using natural convection, from when forced convection is applied at the same temperature. This is summarized in Table 2 and the ANOVA results shown in appendix VI.

Table 2. Effect of Temperature on Moisture Removal Rate (Tukey Method)

When ANOVA was applied to determine the effect of temperature on moisture removal rate (Table 2), it was found that changing temperature from 40 to 45°C caused a significant increase. However, increasing temperature from 45 to 50°C, and 50 to 55°C, in each instance had no significant effect on moisture removal rate.

4. Conclusions

Effect of air velocity, number of trays, grain layer thickness and drying air temperature on dryer performance

Ÿ Moisture removal rate increased with air velocity if grain layer thickness was kept constant. For example, for a grain layer thickness of 0.02 m, moisture removal rate increased from 0.048 to 0.061 kg moisture / (kg wet grain. hour).

Ÿ There was no significant difference in moisture removal rate when number of drying trays was increased from one to two.

Ÿ Moisture removal rate decreased with increase in grain layer thickness as long as air velocity was kept constant. For 0.212 m/s flow rate, as grain layer thickness increased from 0.02 to 0.08 m, moisture removal rate decreased from 0.061 to 0.022 kg moisture / (kg wet grain. hour).

Ÿ Moisture removal rate increased with increase in temperature. However, the increase was only significant at lower temperatures (below 45°C). For example changing temperature from 40 to 45°C caused a significant increase. However, increasing temperature from 45 to 50°C, and 50 to 55°C, in each instance had no significant effect on moisture removal rate.

ACKNOWLEDGEMENTS

This research was funded by the National Council for Innovation, Science and Technology.