Abhik Milan Pal , Subhra Das
Renewable Energy Department, Amity School of Applied Science, Amity University Haryana, Gurgaon, India
Correspondence to: Abhik Milan Pal , Renewable Energy Department, Amity School of Applied Science, Amity University Haryana, Gurgaon, India.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
Abstract
Generation of electricity from solar energy using solar photo-voltaic (PV) cell is a promising and growing field. Energy conversion is maximum when the sun is directly overhead and sunrays fall perpendicularly on a solar PV module. Hence, exact position of the sun in sky throughout a day is an important factor to know while designing and installing a solar panel. In this paper, we present an algorithm to determine altitude and azimuth angles that specifies the sun’s position at any geographical location precisely. It takes latitude, longitude, date and deference of local time from Greenwich Mean Time as input and logically calculates the angles using Microsoft EXCEL. The location of Gurgaon, India is taken as an example for application of the model to display the sun’s path throughout a day in 4 characteristic days in a year and to determine lengths of days from sunrise and sunset times coming also as output. These results can be incorporated in design to orient a solar panel automatically without requiring any cumbersome tracking mechanism.
Keywords:
Latitude, Longitude, Altitude, Azimuth angle, Hour angle, the Sun and Earth movement, Equation of Time
Cite this paper: Abhik Milan Pal , Subhra Das , Analytical Model for Determining the Sun’s Position at All Time Zones, International Journal of Energy Engineering, Vol. 5 No. 3, 2015, pp. 58-65. doi: 10.5923/j.ijee.20150503.03.
1. Introduction
The sun is one of the fundamental energy sources in the universe. In the 21st century, ever increasing energy demand may be fulfilled with the help of solar energy that reaches the earth. Efficient and economic harnessing of clean solar power is very crucial for fulfillment of today’s growing energy need and also helps stop alarming climatic crisis. Every day the sun radiates an enormous amount of energy. It is the primary energy resource for our plant. The earth receives energy from the sun as electromagnetic radiation at extremely large rate [1]. Daily the amount of energy that strikes each country is more than the energy need of that nation for one and a half year [2].Photovoltaic (PV) cell is one of the supreme technologies available now to harness solar radiation and generate electricity. Amount of energy generated from a solar module, consisting of numerous PV cells, depends on radiation quality and angle of incidence of sunrays. A solar module can generate maximum electricity when radiation falls vertically on solar panel [3]. However, difficulty in efficient harnessing arises because of ever changing position of the sun continuously with time and location of the module. So, the most challenging task would be how to tilt the solar module at an angle to the horizontal surface throughout the day to fulfill the requirement of a 90 angle between the rays of the sun and surface of the solar module.Parameters like latitude, longitude, season and time of a day at a given location affect the position of the sun and amount of solar energy reaching the earth’s surface [4] there. In the tropics (between tropic of cancer and tropic of Capricorn) the sun can be either north or south of the solar module. Whether due south or due north depends on exact latitude of the location. So, depending on the above parameters there is a need to know the sun’s position in the sky with respect to a solar PV module. To position a module directly towards the sun at all times, sometimes a solar tracking system is installed to determine the direction of incoming sunrays. But this is not only complicated but also costly. The most common approach though is to compromise and install the module at an optimum tilt angle so that surface of the module is perpendicular to the direction of radiation at solar noon on the equinox day, i.e. the module tilts at an angle equal to the latitude of that location.In this paper we present a method that can exactly calculate the sun’s position at all time zones, i.e. at any time of a day and at any location in the earth. This knowledge may be incorporated in the design of solar PV and thermal system to orient it automatically without requiring any cumbersome solar tracking mechanism.
2. Basics of Earth and Sun Movement
At any location on earth the position of the sun in the sky varies with time because of two basic motions of the earth w.r.t. to the sun: a) the earth revolves around the sun once every year, and b) the earth rotates about its own axis once every day [5]. In fact, the motion of revolution is an ellipse with the sun positioned at one of its foci and the plane of the orbit containing the earth and the sun is called the elliptic plane (Fig. 1). The polar axis, around which the earth spins, is inclined at an angle of 66.55° with the elliptic plane [6], as shown in the figure. Because of the above two motions the position of the sun in the sky changes and the earth experiences different seasons around a year [7]. In fact, there come four important days in a year: 1) June 21 Solstice, 2) September 23 equinox, 3) December 22 solstice, and 4) March 22 equinox. These four days represent the beginning of four seasons [8].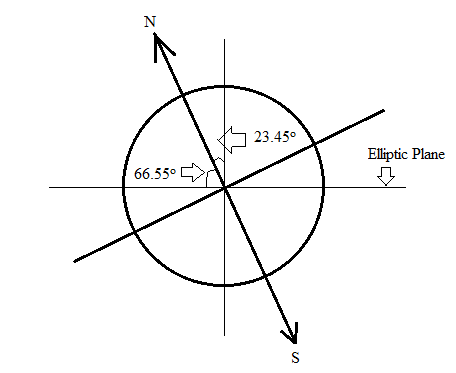 | Figure 1. Earth's Axial Tilt |
Solstice refers to the inclination of the North Pole either towards the sun or away from the sun. On December 22 the North Pole is inclined farthest, by 23.45°, away from the sun, whereas, on June 21 the North Pole is inclined nearest, by 23.45°, towards the sun [9]. This is shown in Figure 2.All areas on earth having latitude more than 66.5°N will be in dark for 24 hours on December 21, whereas, on June 21 the North Pole falls in the illumination area and so the length of the day will be 24 hours.Location at the tropic of Cancer will get maximum radiation on June 21 and the sun will be overhead; it would be summer season at that location [3]. Similarly, on December 21 tropic of Capricorn will observe the sun directly overhead. So December should be summer season for the location lying at the tropic of Capricorn. On the days of solar equinox the sun comes exactly overhead, the sunrays need to travel less distance through the earth’s atmosphere.
3. Sun and Earth Angle
For determining the position of any place on earth and the orientation of the Sun there, two sets of angle [7] [8] have to be specified. The first set, containing two angles, pin points the location on earth. They are: a) latitude, and b) longitude. The second set of angles is related to the position of the sun with respect to a particular location on the earth. These angles are: 1) declination angle, 2) elevation/altitude angle, 3) Zenith angle, 4) azimuth angle, and 5) hour angle. Not all of them are independent, rather related. The position of the sun, hence the direction of the incident radiation at a place, can be calculated if the latitude, longitude, the hour angle and the sun’s declination angle are known. In fact, it will be seen from the following discussions on all the angles that at a given location, specified by its latitude and longitude, the direction of solar radiation will be determined by the elevation and azimuth angles at a given time of a day, quantified by the hour angle, and at a given date of a year, specified by the declination angle.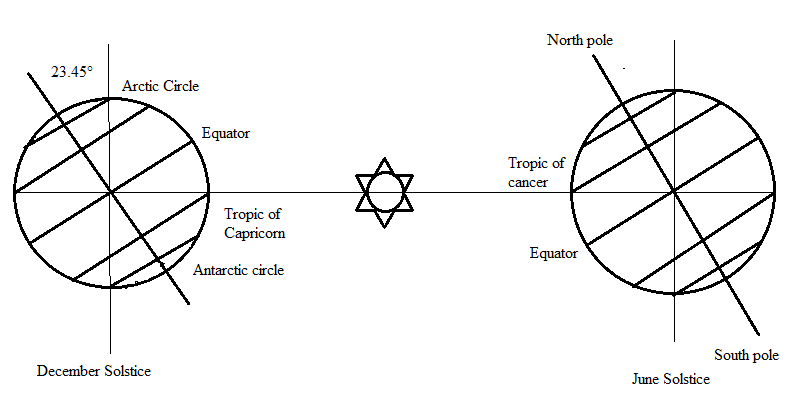 | Figure 2. December Solstice and June Solstice |
3.1. Latitude (ɸ)
The latitude (ɸ) of a place is the angle the radial line joining the place and the center of the earth forms with its projection on the equatorial plane (see Figure 3). The equatorial plane can be said to be a plane with latitude 0o and it bisects the earth into two hemispheres, Northern and Southern.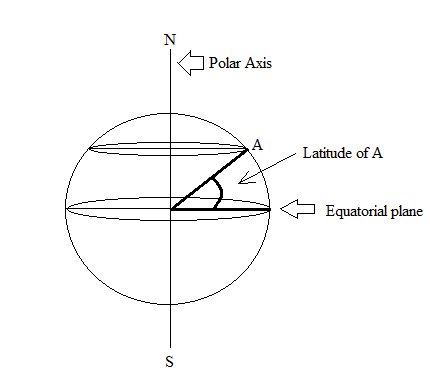 | Figure 3. Latitude Angle |
3.2. Longitude (θ)
There are many imaginary semicircles that can be drawn on the globe from North Pole to South Pole. They are called meridian. The line which passes through Greenwich, England is called the prime meridian line and is taken as the reference meridian line w. r. t. which position of a location on earth is determined. So, the longitude of prime median line is taken as 0°. Longitude of a place is the angular distance of the meridian passing through it from the prime meridian that is, how much angle the two planes, containing each meridian and the center of the earth, subtends. This angle can be east or west of the prime meridian, varying from 180°E to 180°W (see Figure 4).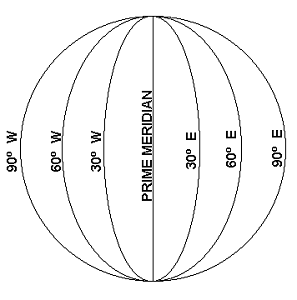 | Figure 4. Longitude Angle |
3.3. Declination Angle (δ)
It is the angle between the lines joining the center of the earth to the sun with its projection on the equatorial plane of the earth. Declination angle varies due to inclination of earth’s polar axis and earth’s revolution around the sun. It gives the position of the sun with respect to the equatorial plane and it depends on day of year, but is independent of location on the earth.Declination angle  varies from -23.45° (December solstice) to +23.45° (June Solstice). The angle is positive when the sun is to the north of the equatorial plane, i.e. when the whole of the Northern hemisphere plus some parts of the Southern hemisphere are illuminated, otherwise it becomes negative. Twice a year (in March and in September) the declination angle becomes zero. Declination angle can be calculated with the help of following equation:
varies from -23.45° (December solstice) to +23.45° (June Solstice). The angle is positive when the sun is to the north of the equatorial plane, i.e. when the whole of the Northern hemisphere plus some parts of the Southern hemisphere are illuminated, otherwise it becomes negative. Twice a year (in March and in September) the declination angle becomes zero. Declination angle can be calculated with the help of following equation: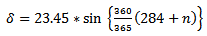 | (1) |
Where n is the number of days in a year starting from 1st January.
3.4. Elevation Angle/ Altitude Angle (α)
The elevation angle 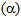 is the angular height of the sun in the sky measured from the horizontal plane at a location on earth [9] [10] [11] as shown in Figure 5. It is zero both at sunrise and sunset and 90° when the sun is directly overhead, which occurs at the equator on spring and fall equinox. This is an important parameter in designing solar PV system.
is the angular height of the sun in the sky measured from the horizontal plane at a location on earth [9] [10] [11] as shown in Figure 5. It is zero both at sunrise and sunset and 90° when the sun is directly overhead, which occurs at the equator on spring and fall equinox. This is an important parameter in designing solar PV system. | Figure 5. Elevation Angle and Zenith Angle |
The elevation angle can be found using following equation:
can be found using following equation: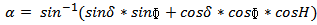 | (2) |
Where, H = hour angle, to be define laterδ= declination angleɸ = latitude of the placeElevation angle at solar noon (when H = 0) is given byα = 90° - ɸ + δ (northern Hemisphere)α = 90° + ɸ - δ (southern Hemisphere)
3.5. Zenith Angle (β)
Zenith angle is the angle between the vertical line at a place on earth and the line joining the place to the sun (see Figure 5). It is related to the elevation angle by the relation: | (3) |
The tilt angle of a PV module should be equal to the zenith angle for maximum illumination.
3.6. Azimuth Angle (γ)
The azimuth angle (γ) is the angular distance of the sun’s projection on the horizontal plane at a place on earth from a reference direction [9] [10] [11]. The angle is measured from the direction of north towards the east (see Figure 6). At solar noon the sun is directly south in the northern hemisphere, whereas it is directly north in the southern hemisphere.Azimuth angle depends on latitude and time of year. The following equation is used to find the angle at any location.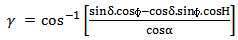 | (4) |
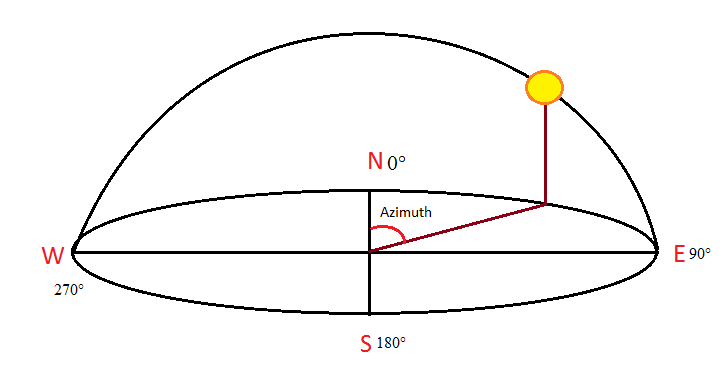 | Figure 6. Azimuth Angle |
At sunrise on the spring and fall equinox, the azimuth angle is 90°. Different authors use different conventions for calculating azimuth angle. In this paper, azimuth angle of the north is taken as zero degree; here all calculations are done using this convention. The azimuth angle is exactly the value of γ obtained from Equation (4) when H, the hour angle defined below, is less than zero otherwise it is (360 – γ) when H is greater than zero.
3.7. Hour Angle (H)
The hour angle (H) is the angle through which the sun moves across the sky. It takes one hour for the sun to cover 15° angular distance in the sky. So, the local solar time (LST) can be converted into the hour angle. Conventionally, the hour angle is zero degree at solar noon, and at other times it is calculated from the relation given below: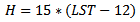 | (5) |
We can see here, the angle is negative before noon and positive after noon.
4. Local Solar Time (LST)
As seen in the previous section, the hour angle depends on the local solar time (LST). Local solar time is, as the name suggests, represents the time of day w.r.t. sun’s position at a given location. It varies from 0 hr to 24 hr approximately, with the noon (12 hr) defined to be the time when the sun’s position is highest in the sky. However, the local time (LT) differs from LST because of - a) the eccentricity of the earth’s orbit, b) human adjustment such as time zone, and c) daylight saving, another human manipulation to change time to use the maximum solar light during a day. So for calculating LST from LT these corrections have to be taken care of.
4.1. Time Zone and Local standard Time Meridian (LSTM)
Time zone [8] [13] is a zone of 15° wide longitude span throughout which only one local standard time is set for human convenience. The set time is the time at the mean latitude of the time zone, called Local Standard Time Meridian (LSTM), and is the calculated from the time of the Prime meridian (longitude = 0°), also called Greenwich Mean Time (GMT). The LSTM, the reference meridian used for a particular time zone, is given by 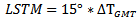 | (6) |
ΔTGMT = difference of the Local Time (LT) from Greenwich Mean Time (GMT) in hours = (LT – GMT). Correction to LST due the Time Zone effect can be calculated using the equation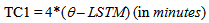 | (7) |
Where 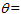 longitude of the location.
longitude of the location.
4.2. Equation of Time (EOT)
The earth’s orbit is not really circular, but an ellipse. So earth’s distance from the sun varies throughout the year. Also, its axis of rotation is not perpendicular to the plane of the ellipse, but tilted. Correction to LST due to these effects can be estimated from the Equation of Time (EOT) [7]. It is the amount by which true solar time (LST) differs from the mean (clock) time (LT) because of this effect. It is given by [12]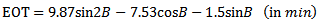 | (8) |
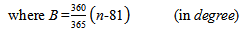 | (9) |
n is the number of days since the start of the year.The total time correction (TC) is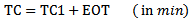 | (10) |
Finally, we get the expression for the local solar time (LST) | (11) |
5. Sunrise and Sunset
Hour angles of sunrise and sunset, ωs, are the angles for which incident sunrays are in the horizontal plane, in other words, altitude angle 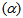 is 0°. Then from Equation (2) we get
is 0°. Then from Equation (2) we get 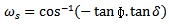 | (12) |
Values of sunrise and sunset hour angles, are same. Then, times of sunrise and sunset can be found using the following equations: | (13) |
 | (14) |
Where TC is the time correction.
6. Determination of Sun’s Position
To calculate the sun’s position in the sky at any location and time, two angles should be known: Azimuth angle and the Altitude angle. Also the sunrise and sunset times will help determining the start and end points of azimuth angle. Different people calculate azimuth angle in different ways. In this paper we follow the convention of azimuth angle starting from zero degree at North Pole. Accordingly east, south and west poles are at 90°, 180° and 270°, respectively. To determine the relevant angles the steps that are to be implemented given are below:Step 1: Define the latitude, longitude, date, local time and time difference of a place as input.Step 2: Check the latitude of the place. If it is east, then take the value of the latitude as positive, else negative.Step 3: Check the longitude. If it is north then positive, otherwise negative.Step 4: According to the date calculate the value of n.Step 5: Find the declination angle using the value of n.Step 6: Calculate the value of B using the value of n.Step 7: Then EOT can be calculated using the value of B.Step 8: Find the LSTM value. Step 9: Using the value of EOT, LSTM and longitude the time correction (TC) can be calculated.Step 10: With help of LT and TC, the LST value can be calculated.Step 11: Get the value of H with the help of LST values.Step 12: Azimuth angle and altitude angle, sunrise and sunset time now can be calculated using the appropriate formulae.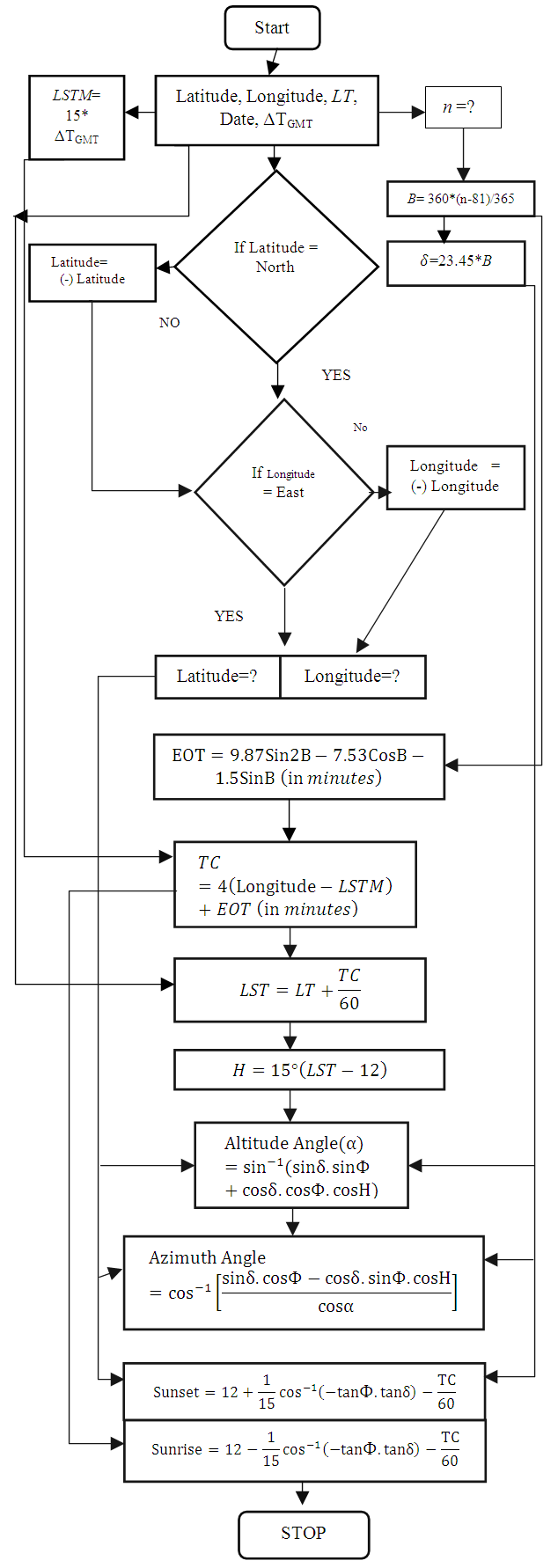 | Following flowchart shows the procedure of calculation in details: |
7. Results and Discussion
Using the methodology presented in the previous section a program has been written which will take latitude, longitude, date and the ΔTGMT as input. It will give altitude angle, azimuth angle of the sun throughout the day as output. Also the sunrise, sunset times and length of the day will be shown. With the help of output data we will be able to understand the path the sun follows for any location on any day. We can also understand the seasonal variation of sun’s path. As an example, Gurgaon location in the state of Haryana in India has been considered. It is located at the Northern hemisphere. Latitude and longitude of Gurgaon is 28.5°N and 77°E, respectively. ΔTGMT value is +5.5 hours.Figure 7 shows the sun path at Gurgaon location on December 22. On that day the sun is located at the tropic of Capricorn in the Southern hemisphere and farthest away from any place in Northern hemisphere. Day length of that day is the shortest in the whole year. The value of the highest altitude angle in a day is also minimum in the year. The sun rises in south-east direction and sunset will be south-west. The azimuth angle varies from 120°SE to 240°SW. Also the rate of change of azimuth angle with respect to time does not vary much.On March 22 the sun is located at the equatorial position of the earth. As seen in the Figure 8, maximum altitude angle on that day will be 61°. Also, the rate of change of azimuth angle increases to a high level during the time period from 11 to 14 hours. Day length is exactly 12 hours. This day the sun rises perfectly in the east and sets in the west. So the span of the azimuth angle is 180°.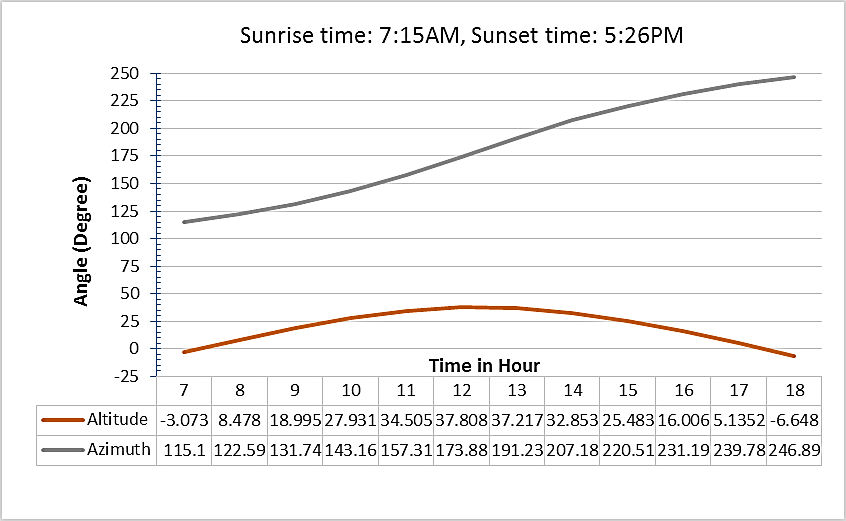 | Figure 7. Sun Position on 22nd December at Gurgaon |
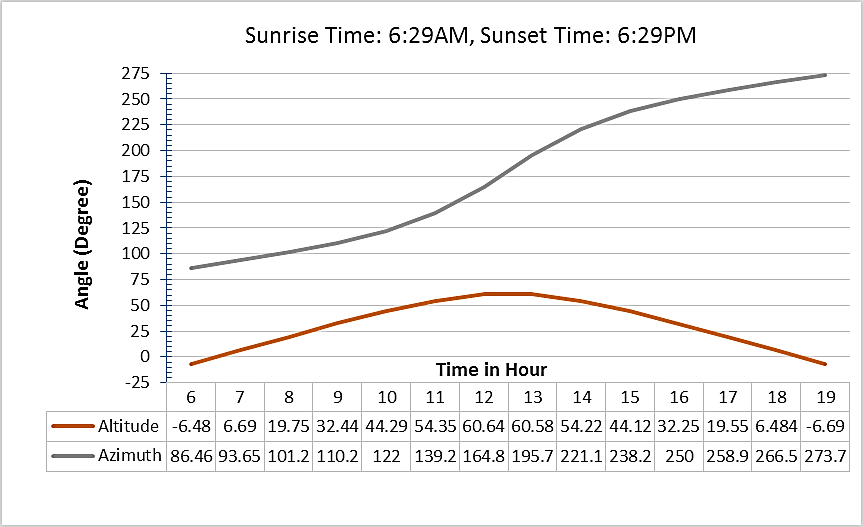 | Figure 8. Sun Position on 22nd March at Gurgaon |
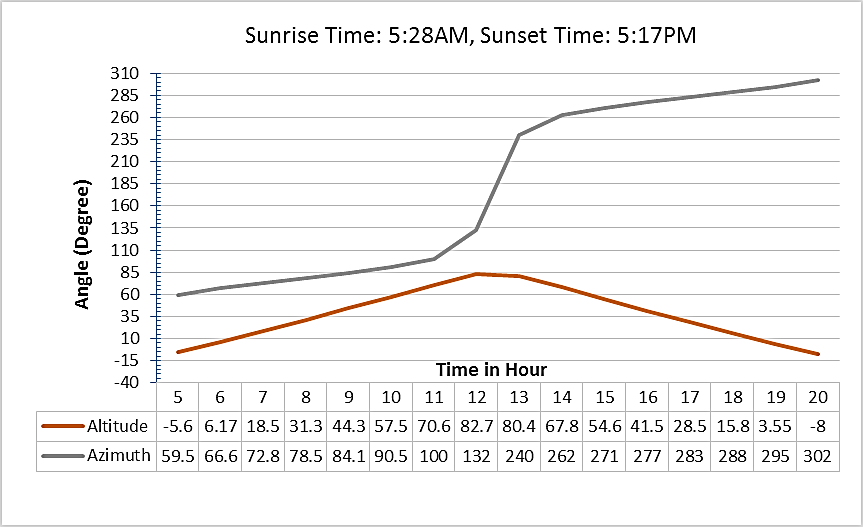 | Figure 9. Sun Position on 21st June at Gurgaon |
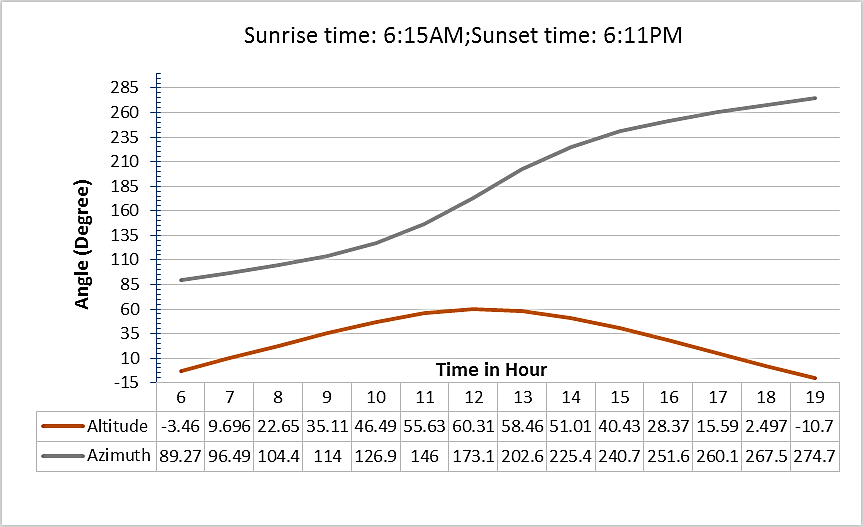 | Figure 10. Sun Position on 23rd September at Gurgaon |
On June 21 the sun is located at Center of Cancer position. On this day the sun is located directly overhead in the Northern hemisphere. As per the Figure 9, between 12 AM to 1:30 PM the sun maintains the altitude angle nearly constant at about 81°. The rate of change of azimuth angle is maximum in that duration. Day length is also maximum, above 12 hours. The range of azimuth angle is about 230° which is maximum in a year. So the sun stays maximum time in the sky.On September 23 the sun again shifts towards the equinox position from Northern Hemisphere. As observed from the figures 8 and 10, the positions and paths of the sun are same on March 22 and September 23.
8. Conclusions
Efficient utilization of solar energy by photo-voltaic (PV) technology envisage proper orientation of PV modules to face the sun directly throughout a day all time in a year. To serve this purpose an algorithm has been developed in Microsoft EXCEL to trace and display position and path of the sun, characterized by azimuth and altitude angles as a function of time, automatically with input parameters of a place. The method has been applied for Gurgaon location in India. From the results of the program we observe that the altitude and azimuth angles vary throughout the year. It is shown that the variation of the angles with time on March 22 and September 23 are identical. The maximum altitude angle in a day also varies throughout a year and is the lowest at 38° on December 22 while it is the highest at 83° on June 21. On December 22 Gurgaon observes the shortest day.The methodology presented in this paper provides a suitable solution to achieve the goal of orienting PV modules to face the sun directly all times. We imagine it to be incorporated directly in a microprocessor based module movement system at any geographical location at any time to predict and follow the sun’s path in a straight forward manner without using any cumbersome, expensive tracking mechanism. Thus it may help most efficient utilization of the sun’s energy using solar PV module.
ACKNOWLEDGEMENTS
We express our gratefulness to the members of the solar energy department of Amity University for their moral support. Our thanks and appreciations also go to those people who willingly helped us out with their expertise whenever we needed.
References
| [1] | http://www.ccpo.odu.edu/SEES/veget/class/Chap_2/2_1.htm |
| [2] | www1.eere.energy.gov/education/pdfs/solar_sunenergy.pdf. |
| [3] | Oloketuyi S idowu, Oyewola M Olarenwaju and Odesola I Ifedayo, “Determination of optimum tilt angles for solar collectors in low-latitude tropical region”, International Journal of Energy and Environmental Engineering, 2013. |
| [4] | Kumarasamy, S, Tulika, S, Guddy, S, Manicam, P: Modelling and estimation of photosynthetically active incident radiation based on global irradiance in Indian latitudes. IJEEE 4, 21 (2013). |
| [5] | “Our solar System: Journey through the universe”, Voyage_G58. |
| [6] | Wu Chun-Sheng, Wang Yi-Bo, Liu Si-yang, Peng Yan-chang and Xu Hong-Hua,” Study on Automatic Sun-tracking Technology in PV Generation.”, DRPT2008, 978-7-900714-13-8/08/. |
| [7] | Chetan Singh Solanki, “Solar Photovoltaics: Fundamentals Technologies and Applications”, PHI Learning Pvt. Ltd., 2009 - Photovoltaic cells. |
| [8] | Martin A Green, “Third Generation Photovoltaics: Advanced Solar Energy Conversion” 1st ed. 2003. 2nd printing Edition Springer 2005. |
| [9] | Seinfeld, John H.; Pandis, Spyros N. (2006). Atmospheric Chemistry and Physics, from Air Pollution to Climate Change (2nd ed.). Wiley. p. 130. ISBN 978-0-471-72018-8. |
| [10] | Duffie, John A.; Beckman, William A. (2013). Solar Engineering of Thermal Processes (4th ed.). Wiley. pp. 13, 15, 20. ISBN 978-0-470-87366-3. |
| [11] | Reda, I., Andreas, A. (2004). "Solar Position Algorithm for Solar Radiation Applications". Solar Energy (Elsevier) 76 (5): 577–589. Bibcode:2004SoEn...76..577R. |
| [12] | Appendix D, Solar radiation, Lab Manual, ebook. |
| [13] | About sunrise and sunset time, timeandday.com, pveducation.org. |
| [14] | Ankit Anuraj and Rahul Gandhi, “Solar Tracking System Using Stepper Motor”, International Journal of Electronic and Electrical Engineering, Volume 7, Number 6 (2014) pp.561-566. |





 varies from -23.45° (December solstice) to +23.45° (June Solstice). The angle is positive when the sun is to the north of the equatorial plane, i.e. when the whole of the Northern hemisphere plus some parts of the Southern hemisphere are illuminated, otherwise it becomes negative. Twice a year (in March and in September) the declination angle becomes zero. Declination angle can be calculated with the help of following equation:
varies from -23.45° (December solstice) to +23.45° (June Solstice). The angle is positive when the sun is to the north of the equatorial plane, i.e. when the whole of the Northern hemisphere plus some parts of the Southern hemisphere are illuminated, otherwise it becomes negative. Twice a year (in March and in September) the declination angle becomes zero. Declination angle can be calculated with the help of following equation: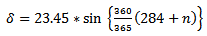
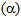 is the angular height of the sun in the sky measured from the horizontal plane at a location on earth [9] [10] [11] as shown in Figure 5. It is zero both at sunrise and sunset and 90° when the sun is directly overhead, which occurs at the equator on spring and fall equinox. This is an important parameter in designing solar PV system.
is the angular height of the sun in the sky measured from the horizontal plane at a location on earth [9] [10] [11] as shown in Figure 5. It is zero both at sunrise and sunset and 90° when the sun is directly overhead, which occurs at the equator on spring and fall equinox. This is an important parameter in designing solar PV system.
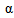 can be found using following equation:
can be found using following equation: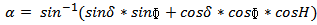

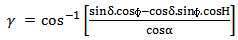

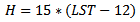
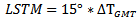
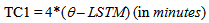
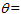 longitude of the location.
longitude of the location.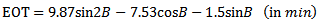
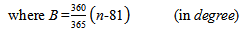
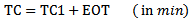

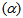 is 0°. Then from Equation (2) we get
is 0°. Then from Equation (2) we get 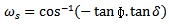







 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML