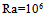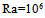Sihem Abidi1, Habib Sammouda1, Rachid Bennacer2
1LabEM (LR11ES34), University of Sousse-Tunisia, ESSTHsousse, Hammam Sousse, Tunisia
2ENS-Cachan Dpt GC/ LMT /CNRS UMR 8535, Cachan Cedex, France
Correspondence to: Sihem Abidi, LabEM (LR11ES34), University of Sousse-Tunisia, ESSTHsousse, Hammam Sousse, Tunisia.
| Email: |  |
Copyright © 2014 Scientific & Academic Publishing. All Rights Reserved.
Abstract
In order to the improve the performance of the hybrid photovoltaic/thermal system,; we proposed to associate a sensor of solar photovoltaic cells to a exchanger. The exchanger is constituted by the two fluids which are separated by the solid wal. The aims of this work are to recuperate the maximum of energy lost by Joule effect using the coolant in contact with photovoltaic cells (fluid 1). The convection and the conduction modes of transfer are established in the level of the roof of the local cavity which filled with air (fluid 2). The phenomena of the heat and the mass transfer have been studied and simulated to obtain the thermal and dynamical fields. The effects of the nature of fluids and of the thermal conductivity of solid are analyzed on the behaviors of coolants and on the efficiency of censor. Results suggested that a better operating performance can be obtained for such system if we optimized the nature and the dimension of coolants (fluid 1) and that of solid wall. The use in the present work, of air as fluid 1 and of a variety of fluid 2, (sodium, lead, air), proved the necessity of optimize the values of the parameters characterizing this system. In effect, that could efficiently generate electricity and thermal energy simultaneously while keeping a moderate temperature to PV cells.
Keywords:
Solar energy, Hybrid photovoltaic/thermal system,Heat exchanger of three coolants, PV cells
Cite this paper: Sihem Abidi, Habib Sammouda, Rachid Bennacer, Numerical Analysis of Three Coolants Heat Exchanger Associated to Hybrid Photovoltaic/Thermal Solar Sensor, International Journal of Energy Engineering, Vol. 4 No. 3, 2014, pp. 45-53. doi: 10.5923/j.ijee.20140403.01.
1. Introduction
In industrialized countries, buildings are great energy consumers, ahead of transport and industrial sectors. The integration of renewable energy systems will be one of the solutions to the key issues of economizing fossil resources, of which world reserves are limited, and reducing the effects of global warming. Solar energy represents the best renewable, environmentally friendly source of energy that can be used for the heating and cooling of houses. But the PV cells presented some drawbacks such as the heating of cell temperature junction and the low PV sensors yield (20 %).Bazilian et al. [1] noted that commercially available PV modules are only able to convert 6-18% of the incident radiation falling on them to electrical energy, with the remainder being dissipated as thermal energy. Otherwise, the convective heat transfer in a closed cavity filled with different boundary conditions, has been extensively studied during the recent years because of the wide application of such a process. Nevertheless, few analyses are required to adapt these convective phenomena to the solar collectors used for the heating during the production of electricity (photovoltaic sensors) which is named the hybrid sensor. Jaballah et al. [2] presented a numerical simulation of a mixed convection in a plane channel partially filled with multi-layers of porous media, with an aim of cooling the photovoltaic cells and of recovering at the same time the quantity of Joule effect wasted heat by these cells, and this is by associating an exchanger to two coolants (fluid and solid) functioning in forced convection. The results show that the degree of penetration of fluid into the porous layer increases with the permeability and the heat transfer decreases as the Darcy number does. Otherwise, some studies used the porous media to store heat collected directly or rejected by PV cells, but there are few authors who use the coolant fluid directly in contact with the cells, exceptionally air is used in several works, but without effectiveness. Ji et al. [3] investigated the combined effects of the solar cell packing factor and the water mass flow rate on the thermal and electrical efficiencies. The simulation results indicated that an optimum of the water mass flow rate existed in the system through which the desirable integrated energy performance can be achieved. Tonui et al [4] presented the use of suspended thin flat metallic sheet at the middle or fins at the back wall of an air duct as heat transfer augmentations in an air-cooled photovoltaic-thermal (PV/T) solar collector to improve its overall performance. The result showed that the FIN type system gives higher thermal output than TMS system. Andersan et al. [5] combined photovoltaic and solar thermal collectors (PVT) to provide electrical and heat energy and thus formed the BIPVT collector. It was shown that key design parameters such as the fin efficiency, the thermal conductivity between the PV cells and their supporting structure and the lamination method had a significant influence on both the electrical and thermal efficiency of the BIPVT. Gan [6] determined with numerical analysis the adequate air gaps for building-integrated photovoltaic. It was found that the mean and the maximum PV temperature decrease with the increase in pitch angle and air gap. Furthermore, the mean PV temperature decreases by increasing panel length for air gaps greater than or equal to 0.08 m, whereas the maximum PV temperature generally increases with the panel length. Thus, without adequate air circulation, over-heating of PV modules would occur and hot spots could be formed near modules with potential cell temperature over 80°C above ambient air temperature under bright sunshine. Some works are developed to ameliorate the exergy due to thermal energy in addition to its 12% electrical output from PV/T system [7] for cold climatic conditions. The possibility of the heat use for climatization makes them attractive for the building integration. Thus, Nicollo et al. [8] presented experimental and theoretical PVT air collector results by translating the basic concepts into efficient and functional technological components and by carrying out a simulation model for performance monitoring of a hybrid PVT air collector. Xu et al. [9] studied numerically a new photovoltaic / thermal heat pump (PV/T-HP) system with modified collector/evaporator (C/E). The results showed that this new PV/T-HP system could efficiently generate electricity and thermal energy simultaneously in both cities during past years. In the same way, Koyunbaba et al. [10] presented a Trombe wall system comparison with PV panel with single, double glass and PV panels. After validation of numerical models with experimental results, these systems will be used in a building for different climatic conditions, glass types and thermal masses. Razvan et al. [11] studied the thermal potential of a thermal system composed by a photovoltaic module BP 585 F mounted at different distances from a wall. The slope of the wall is considered to be 45° and the orientation south. Kamthania et al. [12] evaluated the performance of a hybrid PVT double pass facade for space heating in the composite climate of New Delhi by using a semi transparent PV module. Thermal modeling has been carried out based on the first and second law of thermodynamics in order to estimate the electrical and thermal energy along with the exergy for a “semi transparent” hybrid PVT double pass façade instead of an opaque PV panel. In this context, they suggested that the semi transparent PV module has more electrical efficiency than the opaque PV module. The recent work of the same author’s Abidi et al. in Ref. [13] studied the efficiency of the overall system (PV + exchanger). It was demonstrated that the optimum performance of the system must be both electrical (junction temperature of the PV) and thermal (temperature of the hot air recovered at the outlet of the channel). From this point of view, we propose in this paper to consider the hybrid PVT collector with two coolant fluids separated by pure iron which is a solid coolant interface (from strong thermal conductivity). The first coolant fluid, noted as fluid 1 is in contact with cells and the second one is enclosed in a local building whereas the solid coolant plays the role of the interface between the local and the sensor. We analyzed the correlation between the behaviors of different coolants under the effect of the heat flow exchanged by the PV cells. In fact, the optimization of values for different parameters which characterize this system, will allow to cool the cells and to recover the maximum of heat dissipated by joule effect from PV cells and also to contribute to the improvement of the effectiveness of such a system. The system considered is two dimensional, horizontal and rectangular cavity of height H and length L for aspect ratio A=L/H=7, as presented on the Fig. 1. The upper plate of the cavity receives an irregular heat flux q, while the lower plate is considered as adiabatic and the vertical borders are in free contact with the outside.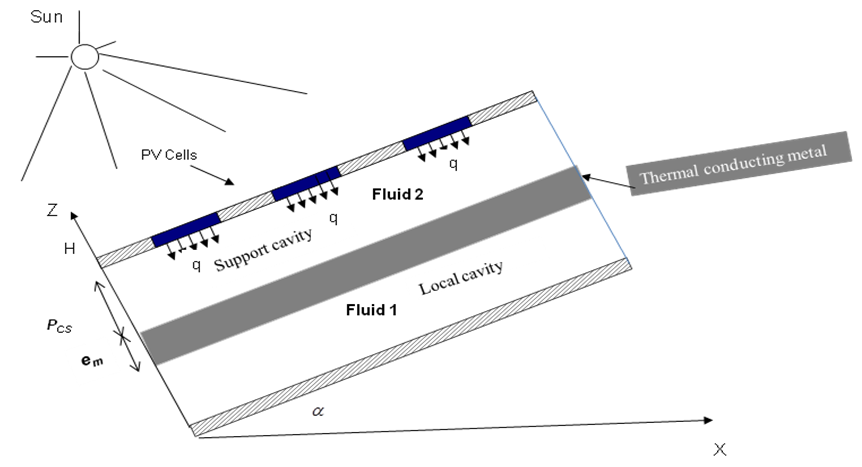 | Figure 1. Schematic diagram of the physical case |
2. The Physical Model and Equations
The system considered is two dimensional, horizontal and rectangular cavity of height H and length L for aspect ratio A=L/H=7. The upper plate of the cavity receives an irregular heat flux q, while the lower plate is considered as adiabatic and the vertical borders are in free contact with the outside.These fluids are supposed to be Newtonian and incompressible, the fluid 1 enclosed in support cavity is characterized by the thermal conductivity λf1 and the convective coefficient hfs1, while the fluid 2 is characterized by λf2 and hfs2, whereas the coolant solid is characterized by λs and its thickness em or his aspect ratio Am=em/H. The flow is considered to be steady and laminar. The thermo physical properties of the fluid are assumed to be constant, except for the density in the buoyancy term, which depends linearly on the temperature, i.e., the Boussinesq approximation is assumed to be valid.
3. Governing Equations
The movement of the fluids and their temperature are governed by continuity, momentum and energy equations in the solid and fluid phases. The heat flux imposed on the up boundary is considered only on the level of PV cells, with density q. Hence, the reference variables for length, velocity, pressure and temperature are chosen respectively as follows: 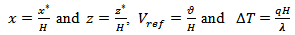 The dimensionless variables are:
The dimensionless variables are: 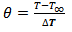 and
and 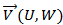 .The dimensionless conservation equations of mass and momentum for the natural convection flow of fluid 1 and fluid 2 are given by:- On the level of the fluid:
.The dimensionless conservation equations of mass and momentum for the natural convection flow of fluid 1 and fluid 2 are given by:- On the level of the fluid: 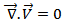 | (1) |
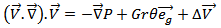 | (2) |
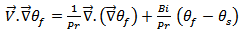 | (3) |
The above equations are related to the fluid.Eq. (3) involves the temperature of the solid 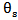 . Thus, an energy equation should be written to determine
. Thus, an energy equation should be written to determine 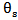 . This equation reads:- On the level of the solid:
. This equation reads:- On the level of the solid: 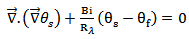 | (4) |
The problem is characterized by the classical Prandtl number, Pr, the Rayleigh number, Ra, the Biot number of each fluid, 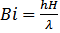 which takes the value zero away from interfaces and the ratio of thermal conductivity
which takes the value zero away from interfaces and the ratio of thermal conductivity 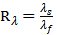 .
.
4. Boundary Conditions
The considered boundary conditions are: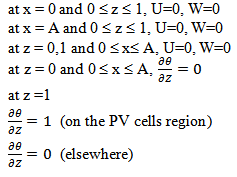
5. Results and Discussions
The governing (Eqs. 1-4) with the boundary conditions were solved using the control finite volume method. The computational domain is divided into rectangular control volumes with one grid point located at the centre of the control volume that forms a basic cell. The set of conservation equations are integrated over the control volumes, leading to a balance equation for the fluxes at the interfaces. A second order scheme is used to discrete the equations; the false transient procedure is used in order to obtain a permanent solution. For faster convergence, the SIMPLER algorithm, originally developed by Patankar [14], is coupled to the SIMPLEC algorithm by van Doormaal and Raithby [15] (see Bennacer [16]). Non uniform grids are used in the program, allowing fine grid spacing near the boundaries. Trial calculations were necessary to optimize the computation time and accuracy. Convergence with the mesh size was verified by employing coarser and finer grids on selected test problems. The convergence criterion is based on both maximum error of continuity equation and the average quadratic residual over the whole domain for each equation was less than a prescribed value ζ (generally less than 10-6).The objective of the present study is to investigate, numerically, the natural convection in a horizontal cavity heated on the top boundary by an irregular flux, q, when the bottom plate is adiabatic. The heat quantity transferred, at position z, is calculated from the average Nusselt number, Nu (z) and a long x direction is defined as: 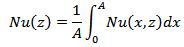 And the average Nusselt number,
And the average Nusselt number, 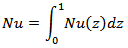 Where
Where 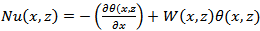 the local heat transfer at any point. Where W is the velocity component along Z axis.
the local heat transfer at any point. Where W is the velocity component along Z axis.
5.1. Validation of Numerical Model
In order to obtain grid independent solution, a grid refinement study is performed for a three spaces. Fig. 2 shows the variation of heat transfer flux, Nusselt number, at the heated surface with grid refinement. It is noted that the results are unchanged beyond 121*41 grid. The present numerical results are evaluated for accuracy against numerical results published in the work reported by Han et al. [17] and experimental one by Elsherbiny [18].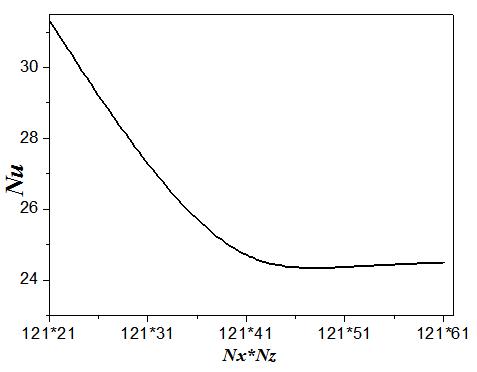 | Figure 2. Influence of the grid on the evolution of the heat transfer for Am = 1/8; Pr=.71; A=7; Bi1=298; Bi2=30; 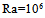 and Acs =1/8 and Acs =1/8 |
In fact, the heat transfer flux, Nu, for laminar natural convective flow in a first space enclosed with air, taken as fluid 1, are calculated for different values of Rayleigh number, Ra. The results are compared, in Fig. 3, to those obtained by identical configuration of published in literature [17, 18]. The agreement is found to be excellent which demonstrates the validity of the formulation and the computer code.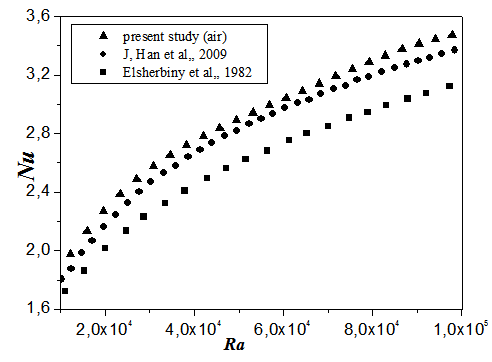 | Figure 3. Numerical and Experimental results of the variation of Nusselt number, Nu, with Rayleigh number, Ra |
The originality of this work is to improve the heat transfer released by PV cells towards the air (fluid 2) of cavity local, and this by the changing the air (fluid 1) by a molten metal imprisoned between PV cells. Fig. 4 illustrates the variation of Nusselt Numbers at first enclosure (fluid 1) for different values of Rayleigh number and for two coolant, air and molten sodium, as fluid 1. The results from the present study are compared in Fig. (4-a) to results using the air coolant [17, 18]. It is noted that heat transfer becomes more important, by changing the air by a molten metal. It is proved that the heat transfer increases according to the conductivity of the coolant, which demonstrates the efficiency of our system. To confirm this more, we presented in Fig. (4-b) the variation of Nusselt Number at the median plane of secondly cavity enclosed of air (fluid 2) for different values of Rayleigh number, and by using molten sodium in first cavity (fluid 1). 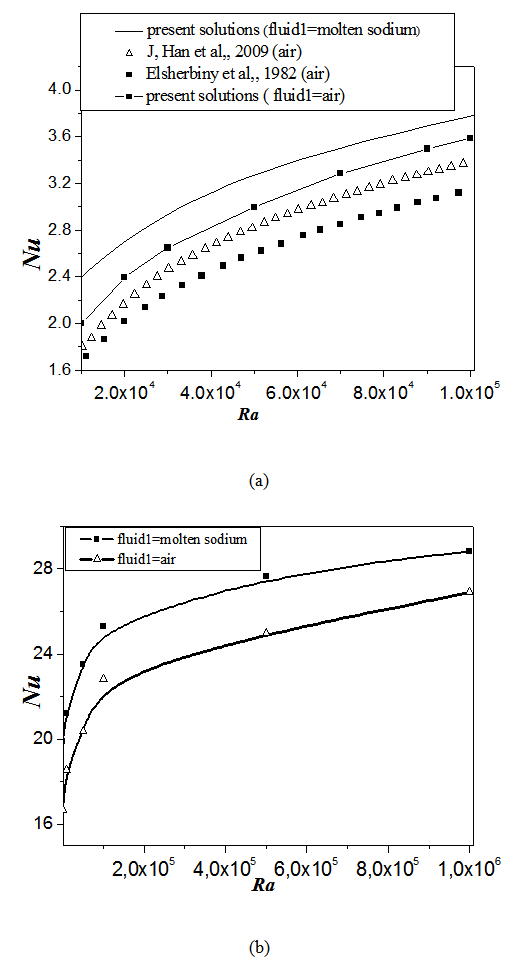 | Figure 4. Variation of Nusselt number, Nu, with Rayleigh number, Ra. for various coolant (Fluid 1): air and molten sodium |
5.2. Parametric Analysis
We focus our study on the analysis of parameters effect: on the heat flow collected, Ra, the aspect ratio of metal plate, Am, the aspect ratio of the cavity support, Acs and the nature of the coolant fluid 1, Bi1 and for horizontal sensor ( α= 0). In the first step, we varied the heat flow through the variation of the Rayleigh number values, Ra=103, 104, 105, 106, for Am=1/8, Acs =1/8, A=7, while using the air on the two compartments with different convective coefficients hf1 and hf2 because of the difference between temperatures: Pr=0.71, Bi1=298; Bi2=30. Isotherms and streamlines are illustrated on Fig. 5 for various values of the Rayleigh number. An overview of these Figures reveals that the increase of the Rayleigh number from 103 to 106, generates a weak variation on the level of dynamic boundary layers. Nevertheless, on the level of the cavity support, the number of the cells of recirculation increases with the heat flow collected. On the other hand, it increases even more in the central zones. This can be explained by the fact that the metal interface does not transmit heat to the local cavity with the same proportion of that transmitted on behalf of the cells PV to the fluid 1. Moreover, the thermal boundary layers disappear gradually with the increase of the Rayleigh number.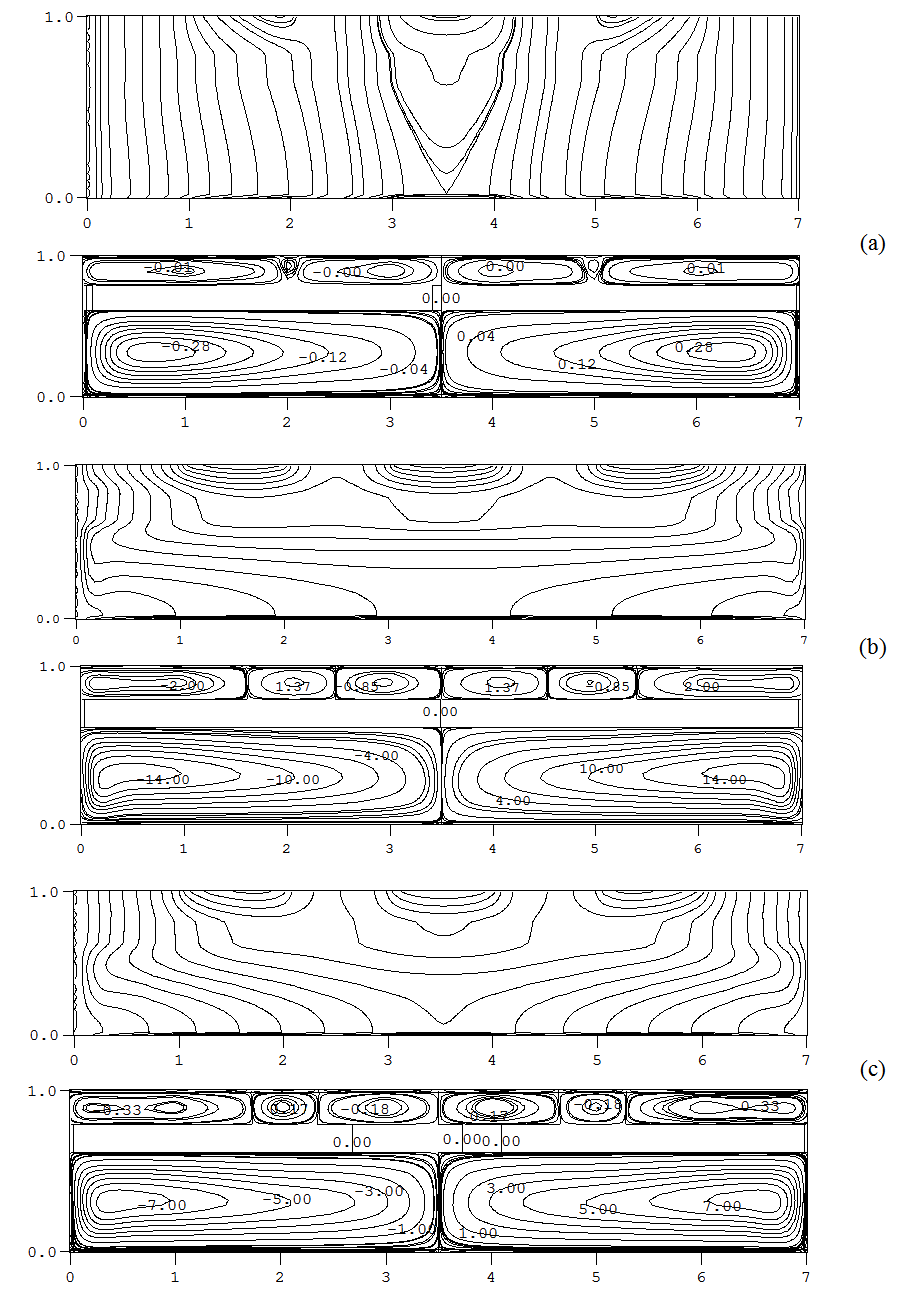 | Figure 5. Isotherms (I) and streamlines (S) for different Ra number: Am = 1/8; Pr=0.71; A=7; Bi1=298; Bi2=30; (a): 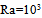 ; (b): ; (b): 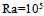 ; (c): ; (c): 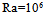 and Acs =1/8 and Acs =1/8 |
In the second step, we varied the thickness of the metal plate through the ratio Am = em / H =1/20, 1/8, 1/4, for Ra =106, Pr=0.71, Bi1=298, Bi2=30 and Acs =1/8. Fig.6 illustrates the temperature profiles to both remarkable positions: at the higher part of the support cavity and at the median plane of the local cavity. It is noticed that the effect of this ratio appears in the two plans. For the higher part of the cavity support, we note that the value of the temperature decreases with the value of Am. Whereas in the median plane of the local cavity, we note that the temperature increases with decreasing Am.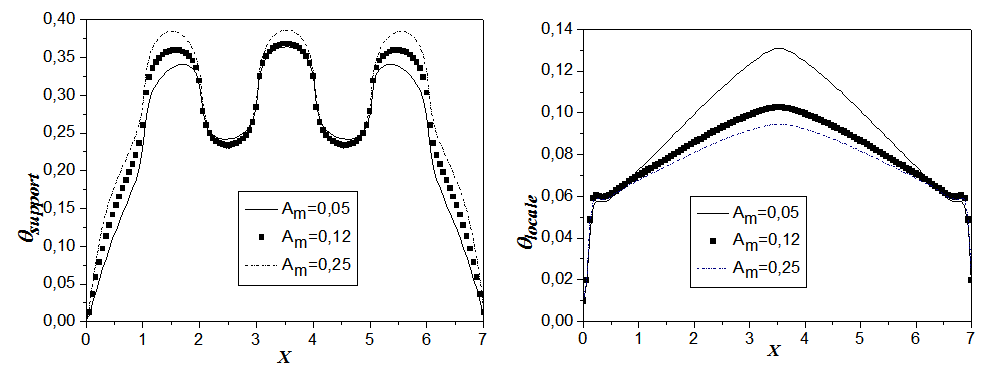 | Figure 6. Aspect ratio of metal plate effects on temperature profiles to the two positions: (a) in the higher part of the support cavity and (b) with the median plane of the local cavity (for 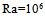 , Pr = 0.71, Bi1 = 298; Bi2 = 30 and Acs = 1/8) , Pr = 0.71, Bi1 = 298; Bi2 = 30 and Acs = 1/8) |
The horizontal profiles of speed and streamlines, for various aspect ratio of metal plate, are represented in Fig. 7; we note that the dynamic boundary layers of the current threads thicken when the value of Am passes from 1/4 to 1/20. Whereas the horizontal speed in the vertical median plane increases and favors the fluid 1 to flow through the local cavity with the decrease of Am, which also permits us to note that for the low values of Am the heat transfer is dominated by natural convection. In the range of the solid plate we can see that there is no flow (null speed), that’s to say the heat transfer is done by conduction. Fig. 8 shows the aspect ratio of metal plate effect on the heat transfer to the horizontal median plane of the local cavity (z= 3/8). We found that the heat transfer decreases when increasing Am. 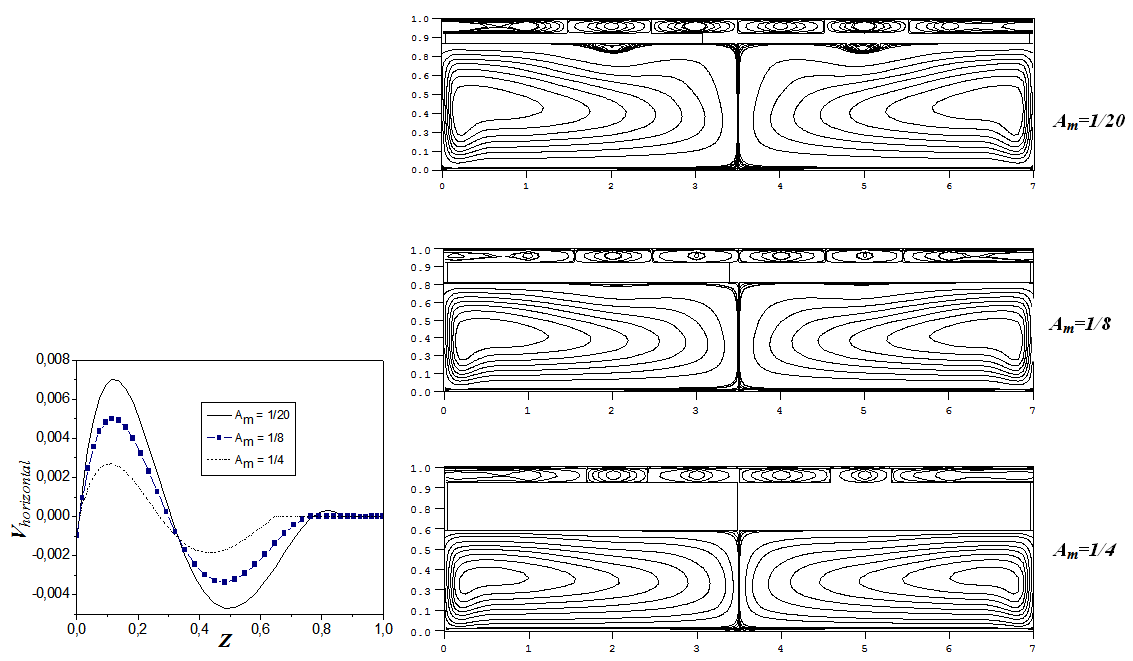 | Figure 7. Effect of aspect ratio of metal plate on the: (a) horizontal speed profiles according to the axis vertical and (b) streamlines flow with: Pr=0.71; A=7; Bi1=298; Bi2=30; 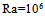 and Acs = 1/8 and Acs = 1/8 |
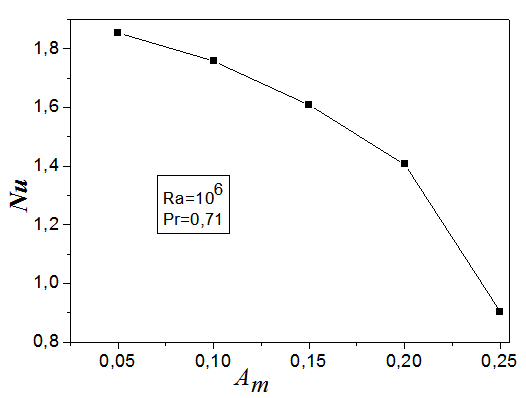 | Figure 8. Variation of the Nusselt number according to Am in the median plane (z=3/8) for A = 7; Bi1=298; Bi2=30 and Acs =1/8 |
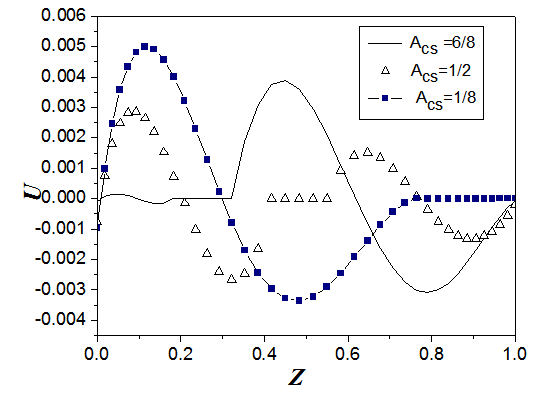
In the Third step, we varied the aspect ratio of the cavity support, Acs =1/8, 1/2, 6/8, for Ra =106, Pr=0.71, Bi1=298; Bi2=30. Fig. 9 shows the temperature profiles in the two remarkable positions: in the higher part of the support cavity and in the median plane of the local cavity. It is noticed that in the higher part of the cavity support we reach the low values of the temperature when the value of Acs is lowered. Whereas in the median plane of the local cavity the temperature increases with decreasing Acs. Using the same data as Fig 9, Fig. 10 illustrates the x- velocity profiles in the median plane. It is noted that when the ratio Acs decreases, the x-velocity is enhanced in the local cavity and decreases in the cavity support. In fact, for the low values of Acs the heat transfer is dominated by natural convection (velocity admits positive and negative extreme).Whereas in the level of the solid plate, the heat transfer is done by conduction (null velocity).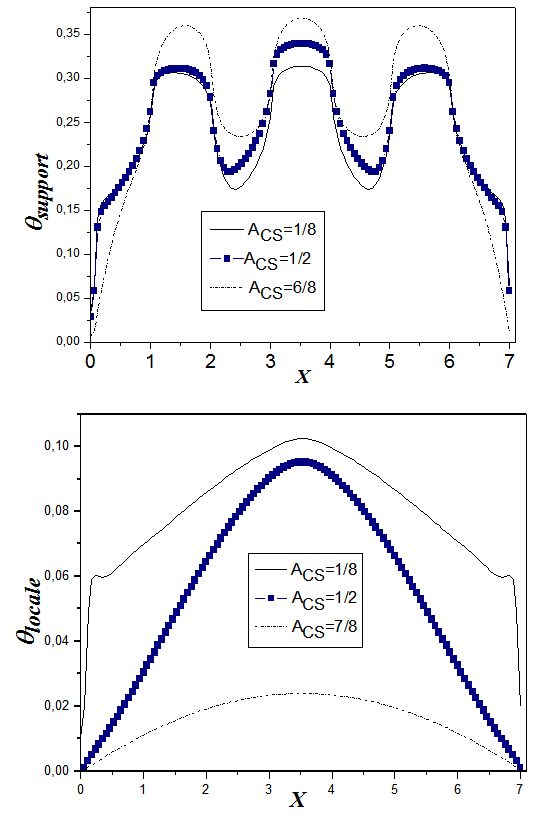 | Figure 9. Aspect ratio of the cavity support, Acs, effect on temperature profiles to the two positions: in the higher part of the support cavity (a) and in the median plane of the local cavity (b) (for Am=1/8, 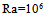 , Pr=0.71, A=7, Bi1 = 298, Bi2=30 , Pr=0.71, A=7, Bi1 = 298, Bi2=30 |
 | Figure 10. Horizontal velocity components in the vertical median plane for different values of aspect ratio of the cavity support, Acs, (=1/8; 1/2 and 6/8) for Am = 1/8; Pr=0.71; A=7; Bi1=298, Bi2=30; 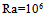 |
Finally, to analyze the effect of the nature of the coolant in contact with PV cells, we change the air by molten metal in the aim to stabilize the flow. This shows the increase of heat transfer according to Biot number in the range 0-1000. Fig. 11 illustrates the evolution of the heat transfer according to Biot number of the fluid 1. It is noticed that the heat transfer increases with Biot number values. Fig. 12 shows the temperature profiles for the two remarkable positions: in the higher part of the cavity support and in the median plane of the local cavity, for Ra =106, Acs = 1/8 and Am = 1/8, and for the three coolants. We note that in the vicinity of PV cells, the temperature decreases when the conductivity of the coolant increases. Whereas in the local cavity we notice that the temperature strenghens with the conductivity of the coolant, which is the objective of work. These results prove that the molten metals are good thermal conductors which explain the use of salts from sodium as a coolant fluid for the cooling of the nuclear reactors. 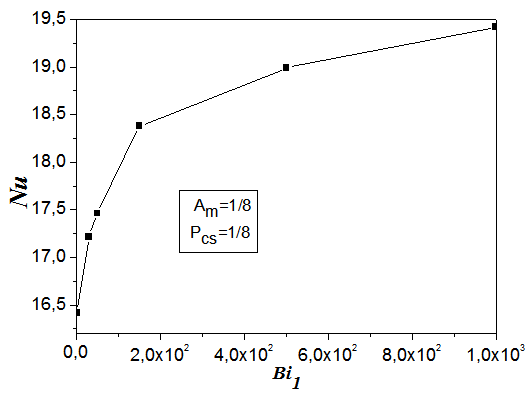 | Figure 11. Effect of nature of coolant fluid (Biot number, Bi1) on the average heat transfer (average Nusselt number, Nu), for A=7; 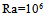 and Bi2 and Bi2 |
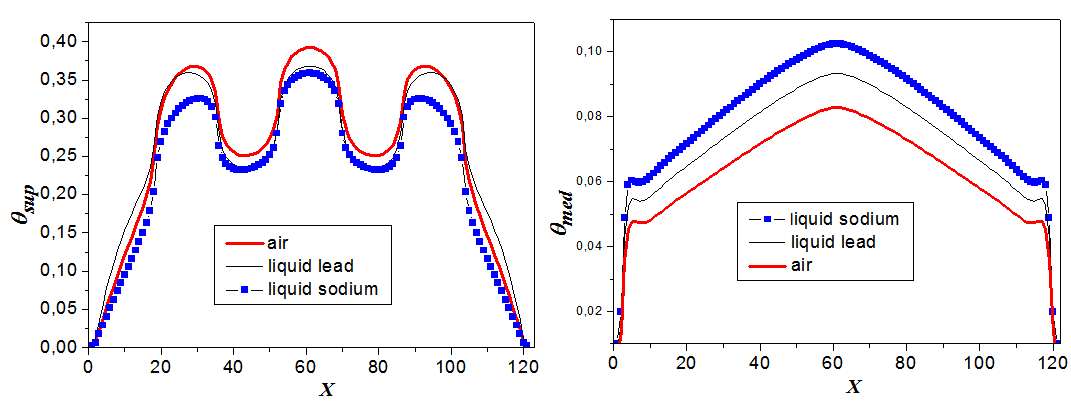 | Figure 12. Effect of nature of coolant fluid on temperature profiles at two positions: (a) near and below the PV cells, and (b) in the median plane of the local cavity, for optimal configuration Acs = 1/8, Am = 1/8, 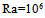 |
6. Conclusions
To improve the performance of the hybrid photovoltaic / thermal system, a new exchanger of three coolants, two fluids and one solid, is associated with a sensor of solar photovoltaic cells.The aim of this work was to cool the cells and simultaneously to recover the maximum of heat dissipated by joule effect from PV cells which implies the improvement of the efficiency of such a system. The results show that the good choice of the fluid coolant in contact with the photovoltaic cells will make it possible to recover the maximum of heat released by Joule effect. In addition, the optimization of the thermal characteristics of the coolant solid is necessary to guarantee a good heat transfer such as the thermal conductivity and its thickness. Finally, this study will permit to optimize the nature and the dimension of different components of such a system. In fact, we have shown the big improvement introduced on the level of the cooling of PV cells and the heating of the local cavity when we changed the air by molten metal (sodium and lead in the liquid state).
7. Nomenclature

References
| [1] | M.D. Bazilian, H. Kamalanathan, D. Prasad. Thermographic analysis of a building integrated photovoltaic system, Renewable Energy. 26 (2002) 449-461. |
| [2] | S. Jaballah, R. Bennacer, H. Sammouda and A. Belghith. Numerical simulation of mixed convection in a plane chanel partially filled with a porous media and subjected to an irregular heat flux, Journal of porous media. 11(3) (2008) 247-257. |
| [3] | Jie. Ji, Jun. Han, Tin-tai. Chow, Hua. Yi, Jianping. Lu, Wei. He, Wei. Sun. Effect of fluid flow and packing factor on energy performance of a wall-mounted hybrid photovoltaic/ water-heating collector system, Energy and Buldings journal. 38 (2006) 1380-1387. |
| [4] | J.K. Tonui, Y. Tripanagnostopoulos. Improved PV/T solar collectors with heat extraction by forced and natural air circulation, Renewable Energy. 32 (2007) 623-637. |
| [5] | T. N. Anderson, M. Duke, G.L. Morrison, J.K. Carson. Performance of a building integrated photovoltaic/thermal (BIPVT) solar collector, Solar Energy Journal. 83 (2009) 445-455. |
| [6] | G. Gan. Numerical determination of adequate air gaps for building-integrated photovoltaics, Solar Energy Journal. 83 (2009) 1253-1273. |
| [7] | A.S. Joshi, A. Tiwari. Energy and exergy efficiencies of a hybrid photovoltaic-thermal (PV/T) air collector, Renewable Energy. 32 (2007) 2223-2241. |
| [8] | N. Aste, G. Chiesa, F. Verri, Design. development and performance monitoring of a photovoltaic-thermal (PVT) air collector, Renewable Energy. 33 (2008) 914-927. |
| [9] | G. Xu, S. Deng, X. Zhang, L. Yang, Y. Zhang. Simulation of a photovoltaic/thermal heat pump system having a modified collector/evaporator, Solar Energy. 83 (2009) 1967-1976. |
| [10] | B. K. Koyunbaba, Z. Yilmaz. The comparison of trombe wall systems with single glass, double glass and PV panels, Renewable Energy. 45 (2012) 111-118. |
| [11] | I. Razvan. Caluianu, F. Baltaretu, Thermal modeling of a photovoltaic module under variable free convection conditions, Applied Thermal Engineering. 33-34(2012) 86-91. |
| [12] | D. Kamthania, S. Nayak, G.N. Tiwari, Performance evaluation of a hybrid photovoltaic thermal double pass facade for space heating , Energy and Buildings. 43 (2011) 2274–2281. |
| [13] | S. Abidi, H. Sammouda, R. Bennacer. Thermal Study of a Covered and Hybrid Photovoltaic Sensor Associated with a Heat Exchanger, International Journal of Materials Engineering., 3(6) ( 2013) 113-123. |
| [14] | S. Patankar. Numerical Heat Transfer and Fluid Flow, New York, 1980. |
| [15] | J. P. Van Doormaal, G.D. Raithby. Enhancements of the simple Method for predicting incompressible fluid flows, Numerical Heat Transfer. 7 (1984) 147-163. |
| [16] | R. Bennacer. Convection naturelle thermosolutale : simulation numérique des transferts et des structures d’écoulement, Doctoral thesis. University of Paris 6, France 1993. |
| [17] | J. Han, L. Lu, H. Yang. Thermal behaviour of a novel type see-through glazing system with integrated PV cells, Building and Environment. 44 (2009) 2129-2136. |
| [18] | S.M. Elsherbiny, G. D. Raithby, KG. Hollands. Heat transfer by natural convection across vertical and inclined air layers, ASME J. heat transfer. 104 (1982) 96-102. |


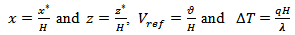 The dimensionless variables are:
The dimensionless variables are: 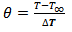 and
and 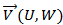 .The dimensionless conservation equations of mass and momentum for the natural convection flow of fluid 1 and fluid 2 are given by:- On the level of the fluid:
.The dimensionless conservation equations of mass and momentum for the natural convection flow of fluid 1 and fluid 2 are given by:- On the level of the fluid: 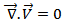
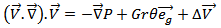
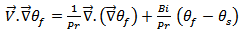
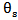 . Thus, an energy equation should be written to determine
. Thus, an energy equation should be written to determine 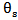 . This equation reads:- On the level of the solid:
. This equation reads:- On the level of the solid: 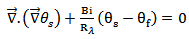
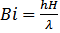 which takes the value zero away from interfaces and the ratio of thermal conductivity
which takes the value zero away from interfaces and the ratio of thermal conductivity 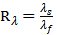 .
.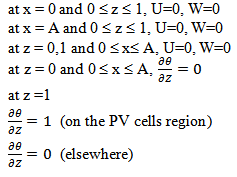
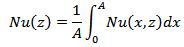 And the average Nusselt number,
And the average Nusselt number, 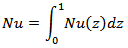 Where
Where 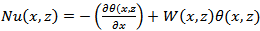 the local heat transfer at any point. Where W is the velocity component along Z axis.
the local heat transfer at any point. Where W is the velocity component along Z axis.
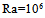 and Acs =1/8
and Acs =1/8


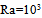 ; (b):
; (b): 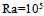 ; (c):
; (c): 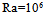 and Acs =1/8
and Acs =1/8
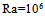 and Acs = 1/8
and Acs = 1/8

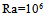 and Bi2
and Bi2
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML
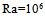 , Pr = 0.71, Bi1 = 298; Bi2 = 30 and Acs = 1/8)
, Pr = 0.71, Bi1 = 298; Bi2 = 30 and Acs = 1/8)
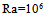 , Pr=0.71, A=7, Bi1 = 298, Bi2=30
, Pr=0.71, A=7, Bi1 = 298, Bi2=30