M. M. Hadjiat1, S. M. A. Bekkouche2, A. Zerga3, B. Benyoucef3, M. R. Yaiche1
1Centre de Développement des Energies Renouvelables, CDER, Algiers, 16340, Algeria
2Unité de Recherche Appliquée en Energies Renouvelables, URAER, Centre de Développement des Energies Renouvelables, CDER, Ghardaïa, 47133, Algeria
3Materials and Renewable Energy Development Unity, University Abou Bakr Belkaïd, Tlemcen, Algeria
Correspondence to: M. M. Hadjiat, Centre de Développement des Energies Renouvelables, CDER, Algiers, 16340, Algeria.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
In this paper a mathematical model has been developed to study thermal behaviour of an Integrated Collector Storage (ICS) solar water heater. The ICS system consists of one cylindrical horizontal tank properly mounted in a stationary symmetrical Compound Parabolic Concentrating (CPC) reflector through. This model allows the computation of stored water mean temperature. A computer code is designed to solve the governing energy equations and used to simulate an ICS system at Ghardaïa in southern Algeria, The effect of inclination angle on the thermal performance of such ICS system is studied.
Keywords:
ICS Solar Water Heater, CPC, Mean Water Temperature, Modelling
Cite this paper: M. M. Hadjiat, S. M. A. Bekkouche, A. Zerga, B. Benyoucef, M. R. Yaiche, A New Modelling Approach of an ICS Solar Water Heater with CPC Reflectors, International Journal of Energy Engineering, Vol. 3 No. 3, 2013, pp. 165-170. doi: 10.5923/j.ijee.20130303.06.
1. Introduction
The flat plate thermosiphon unit (FPTU) and integrated Collector Storage (ICS) system constitute low temperature (40-70°C) solar water heater that is able to offer up to 200 litres per day of domestic hot water need. Their simple construction combined with high thermal performances made FPTU the option of first choice. Because of their high thermal losses in storage tank, ICS solar water heaters are not frequently used[1]. Nonetheless, in Algerian desert characterised by the availability of solar resources and little drop in diurnal temperature render the use of ICS more attractive and thus promoting heating systems based renewable energies in this region.Several works have been conducted to investigate thermal performances of different types of ICS systems. In Greece, Tripanagnostopoulos et al.(2002)[2] investigated some ICS systems which consisted of single and double cylindrical tanks horizontally placed in truncated CPC reflector troughs in order to achieve efficient, practical and low cost solar water heater. Smyth et al.(2004)[3] presented an experimental study of an ICS system in Northern Irish climate. F. Fooladi and H. Taheriani (2010)[4] report the performance of a multi-tube ICS solar water heater in northern Iran. In a published work by M. Souliotis et al.(2004)[5], the experimental results showed that by using high transmitivity transparent cover coupled with high reflectance of its reflective surface an ICS system with selective absorbing surface gave a comparable thermal performances to that obtained through the use of FPTU with selective absorber.A M. Souliotis et al. (2009) study[6], in which a suitable artificial neural network (ANN) and TRNSYS are combined in order to predict the performance of an Integrated Collector Storage (ICS) prototype. It was shown that this new method can be used effectively for such predictions. Other papers have been published in literature about experimental study of an ICS solar water heater but we had not found in our literature any theoretical studies of such system.In this paper, a numerical method to study the transient behaviour of an ICS solar water heater with CPC reflector subjected to typical semi- arid climate (Ghardaia) is used. In fact a mathematical model was proposed and tested using computer code. Theoretical and experimental results are compared and inclination angle of the device is discussed.
2. Description of an ICS Solar Water Heater
The CPC type reflector is the ideal non-imaging light concentrator that allow acceptable concentration ration without need of tracking system. Beside its capability of concentrating direct radiation CPC is able also to concentrate a fraction of diffuse radiation. Only two parameters are needed to specify the complete geometry of a fully developed (i.e., non-truncated) CPC namely, the radius R of the cylindrical absorber and the acceptance angle, θc. Any solar radiation incidence within the acceptance angle, with the help of parabolic reflector can reach the absorber. According to the above referenced parameters R and θc, the analytic equations of the reflector parts, based on the rectangular axis system O, x, y, are as follows[7]: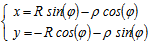 | (1) |
Where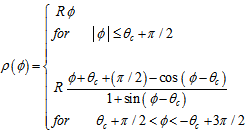 | (2) |
The geometric concentration ratio is defined as follows: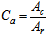 | (3) |
Where Ac is the aperture surface area of the system and Ar is the cylindrical tank surface area. The basic design of the proposed ICS system is shown below in Figure 1.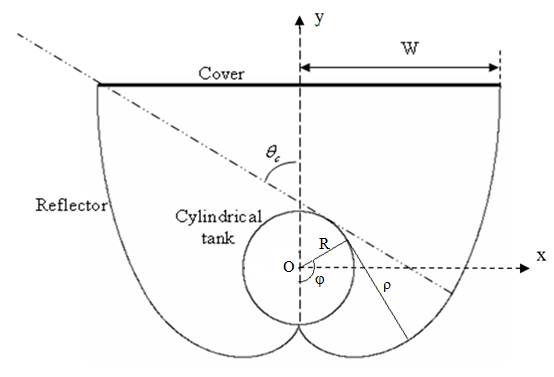 | Figure 1. Cross section of ICS system |
The prototype consists of symmetrical CPC reflector whose line focus in a cylindrical tank of radius R. The tank is covered with selective surface with high solar absorption and low thermal emission. A transparent cover may be fitted across the aperture of the concentrator to protect the reflecting film from deteriorating and to reduce the rate of heat loss from the absorber. The underside of the reflector is thermally insulated to reduce heat losses. Radiation reflection from the parabolic reflector is taken into account by the apparent reflectance 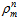 .n : representing an average number of reflections for a CPC. θc : represents the acceptance angle.The prototype geometrical dimensions are length L and width 2W.
.n : representing an average number of reflections for a CPC. θc : represents the acceptance angle.The prototype geometrical dimensions are length L and width 2W.
3. Modelling
Before modelling the prototype, the following main assumptions are considered in order to simplify the analysis.■ The ICS system is free from fabrication errors.■ The transparent cover and the cylinder tank have uniform temperature distribution and the CPC component properties are independent of the temperature.■ For any given direction of light source, a certain fraction of the rays entering the aperture will reach the absorber directly, while the other rays will reach the absorber after one or more reflections. Therefore one can define an average number of reflections n for a CPC[8].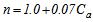 | (4) |
The energy balance equation of the system may be written as:Glass cover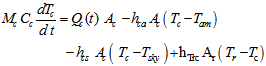 | (5) |
Where Qc(t) is the solar radiation absorbed by the cover which is defined according to Hsieh’s theory[8] by using the following expression: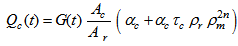 | (6) |
The heat loss coefficient by convection hca between the cover and the ambient, and the radiative heat loss coefficient hcs between the cover and the sky are calculated from relationships 7 and 8, respectively[9]: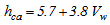 | (7) |
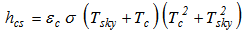 | (8) |
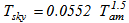 | (9) |
In equation (5), hTrc is the transfer coefficient between the cylindrical tank and the cover. It usually consists of two parts, namely the convective part and the radiative part. For the configuration under the mentioned considerations, the following relation may be written: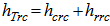 | (10) |
Where the convective part hcrc and the radiative part hrrc are given by relation 11 and 12, respectively[9]: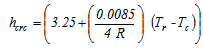 | (11) |
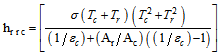 | (12) |
Cylindrical tankThe energy balance of a cylindrical tank is established by using formula 13: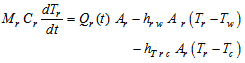 | (13) |
Where Qr(t) is the radiation absorbed by cylindrical tank which is defined according to Hsieh’s theory[8] by using the following expression: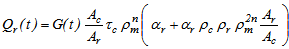 | (14) |
The factor hrw appearing in equation 13 is the convective heat transfer coefficient from the cylindrical tank to the water. It's defined as[10]: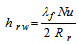 | (15) |
In laminar regime, i.e. 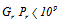
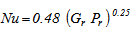 | (16) |
In turbulent regime, i.e. 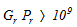
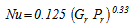 | (17) |
Where,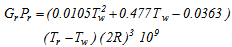 | (18) |
Stored waterIn this case, there is no extraction of water from the storage tank. The average storage water temperature will be calculated by equation 19.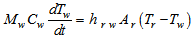 | (19) |
4. Experimental
 | Figure 2. View of experimental system |
A low cost ICS solar water heater with CPC reflectors was designed, constructed and tested in Ghardaïa (32.4N, 3.6E) (fig.2). The storage tank is mounted in symmetric curved reflector troughs. The entrance for the water is situated at the bottom and the exit is situated at the top of the other side. The dimensions of cylindrical tank are R=0.2m, L=1m and the acceptance angle is θc = 90° (Ca = 1). We used polished stainless steel with reflectivity ρm= 0.68 to form the designed reflectors and the absorbing surface is painted matt black (αr = 0.9; εr = 0.9). The figure below illustrates the view of ICS system.Experimental measurements of water storage tank temperature are carried out. To proceed, two positions of thermocouples inside the storage tank have been chosen, the first thermocouple is placed at the top of the tank, and the second one is placed at the bottom of the tank. The resulting temperature is the average of these values. Figure 3 shows the measured temperatures of the water inside the storage tank versus time. Values were collected in accordance with the ASHRA standards.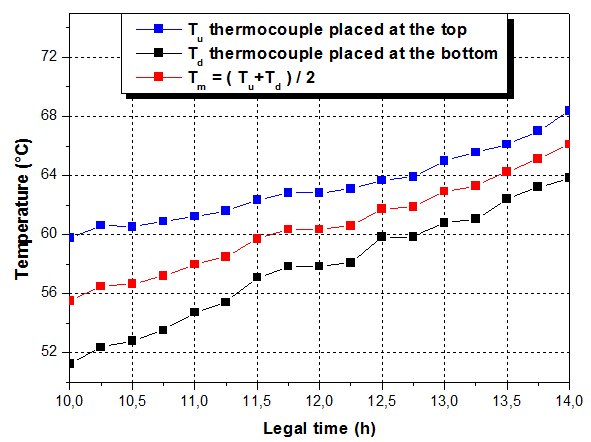 | Figure 3. Experimental water temperature for June 28, 2011 |
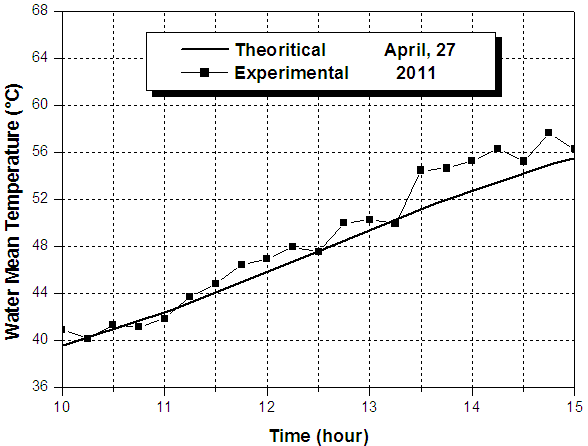 | Figure 4. Experimental and theoretical mean water temperature for 27 April 2011 |
Obtained values will be compared with those calculated by the designed simulation program. The four order Runge Kutta method was used to solve numerically the energy equilibrium equations. For this purpose, a computer simulation program based on a mathematical model was developed. Figure 4 illustrate the thermal profile of stored water for 27 April 2011 from 10: pm to 15: pm.Any measurement made with a measuring device is approximate. So we sought to evaluate the error in the water temperature measured inside the tank. It is reasonable to plot in figure 5 the relative error versus temperature to predict the validity of calculations.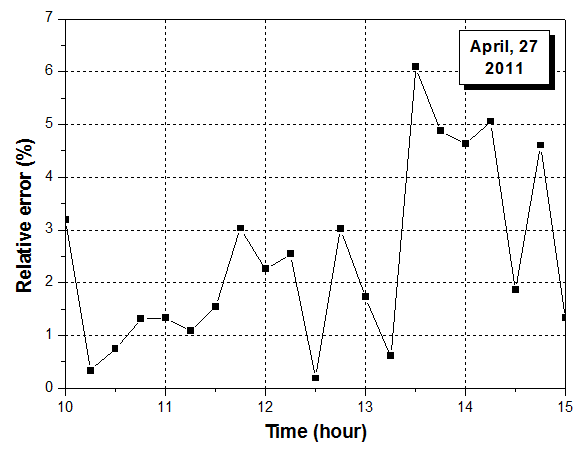 | Figure 5. Relative error, April 27, 2011 |
It is known that heat transfer through the lead wires of a thermocouple conducts to error in the measured temperature. Errors may occur due to surface radiation, especially at elevated temperatures, to conduction error in thermocouple, to geometrical defects and to the viscous dissipation effects that may be important. Despite these obstacles, the concordance between theory and real world is so encouraging.
5. Meteorological Data, Results and Numerical Simulation
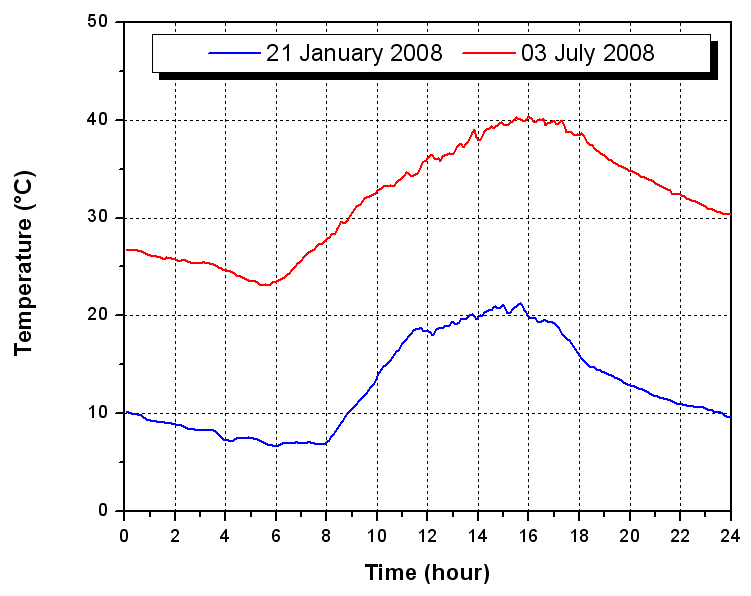
Ghardaïa city (32.4° N, 3.8° E) is a dry and arid site, characterized by an exceptional sunshine, most often. It has a very important rate of insolation (75% on average) and the mean annual of global solar radiation measured on horizontal plane exceeds 5.5 (kWh/m2). The sunshine duration is more than 3000 hours per year, which promotes the use of solar energy in various fields[11-19]. The use of directly experimental results provided by a station located in the site where studies are carried out is preferred because it allowed having more precise and better estimation of global irradiation and ambient temperatures on the system. Sun-Tracker is a station with high precision comprises two parts: a fixed part consisting of an EKO type Pyranometer for measuring global solar irradiation received by a horizontal surface, and a mobile part based on a robotic system capable to follow the trajectory of the sun from sunrise to sunset.Figures 6 and 7 present instantaneous variations of the incident solar irradiations and ambient temperature respectively under clear sky condition. These values correspond the day of 25 January and 03 July in the year 2008. This tow important parameters, ambient temperature and solar irradiations, are introduced in the computer program for numerical simulation of the ICS system. However, in our numerical simulation, the ambient temperature data are taken from experimental measurement and solar irradiations are computed by using Capderou model under clear sky. In this model, we had determined the global irradiation of days mentioned above for tow specific inclination angle according to the site of Ghardaïa: annual optimal angle (32,4°) and mensual optimal angle of January month (53,4°) .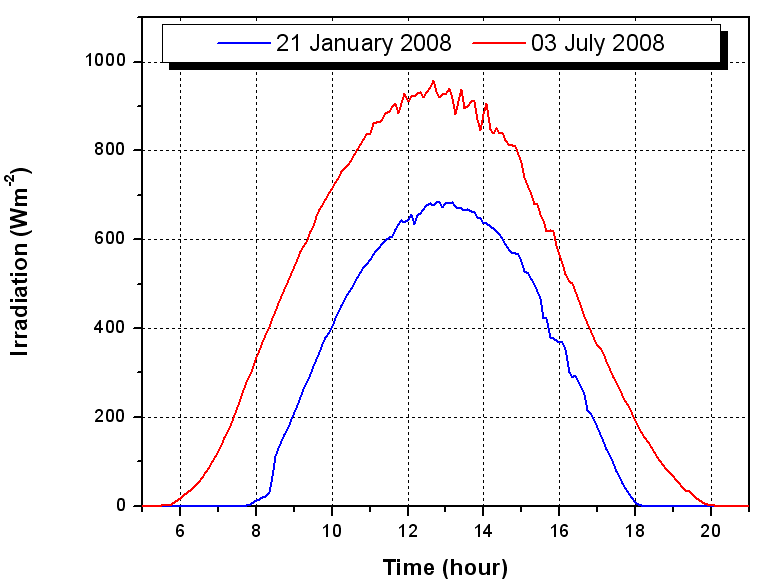 | Figure 6. Global horizontal irradiation given by sun tracker station |
 | Figure 7. Ambient temperature |
The numerical results are carried out by employing the values of the relevant parameters as follows: W=0.7 m; L=1 m; R=0.2 m; er=1.5×10-3 m; ec=3×10-3 m; αc= 0.05; αr = 0.85; τc= 0.9; ρc= 0.05; ρr= 0.15; ρm= 0.9; εc= 0.85; εr=0.05.Before calculations, we assume that the initial mean water temperature start the first day equal to ambient temperature and wind speed Vw is constant Vw= 5 ms-1.We present in figure 8, the results of numerical simulations for a sequence of one day operation of an ICS system in January and for two different inclination angle (32.4° and 53.4°). However, the water temperature variation for an ICS system in July is illustrated in figure 9. At first, it shows that the water temperature profile depends on the inclination angle. According to the saharan climate, the hot water is not so required during the summer. Then, it is recommended to choose the January optimal angle or to take the inclination angle of the solar water heater as follow: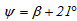 | (20) |
where β is the latitude of the site.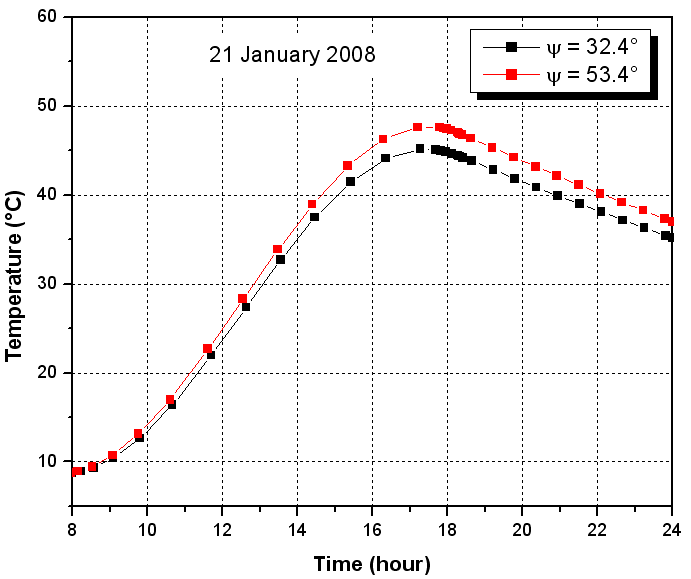 | Figure 8. Mean water temperature profile in January without water drain |
 | Figure 9. Mean water temperature profile in July without water drain |
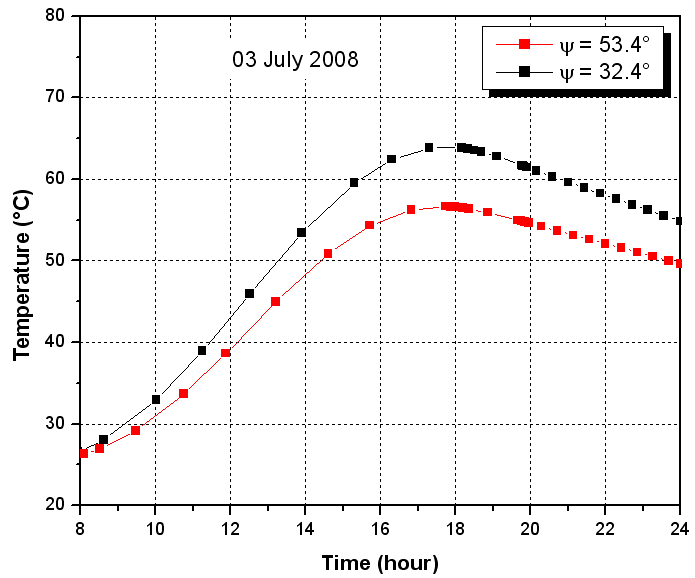
To facilitate studies about this device, computer program has been conceived and developed in the EXCEL spreadsheet software. The main feature of the software is that it can be used to determine the instantaneous values of solar intensity and solar energy incident. To do this, we have adopted and chose two theoretical approaches that are valid for a completely clear sky. Spreadsheet software for calculating radiation in Excel for 48 Wilayas of Algeria have been designed and developed to include all results and facilitate the numerical simulation. In this case, simulation includes all methods that can reproduce the processes of a system in a digital mode. Though we can use this simulation to study this aspect qualitatively, it is crucial for us to use the numerical results of such simulation to illustrate further conclusion. In these situations, the result of the simulation can have a good representation of the real environment. From the result we can safely draw proper conclusions and have a better understanding of the system[13, 15].The computer software gives the possibility to calculate the incident instantaneous irradiance on any plane:- on a plane with fixed orientation and variable angle of inclination- on a plane with fixed angle of inclination and variable orientation- on a plane at vertical incidence which undergoes a solar tracking. Figure 10 gives an overview of the simulated water temperature; the chosen day corresponds to January 25 for a totally clear sky | Figure 10. Mean water temperature profile |
According to these results, we see that high temperatures correspond to the largest incident energy. Therefore, it is helpful to find the average temperatures of the water in the case where the system undergoes a solar tracking. The proposed computer software can be coupled with a professional interface that is manipulated by a user-friendly scientists, architects and teachers. The advantage of this software is to integrate the calculated data for optimizing thermal and photovoltaic solar systems.
6. Conclusions
Integrated Collector Storage solar water heaters based on horizontal cylindrical storage tank and CPC reflector were designed, constructed and tested. The mathematical model proposed in the present work has been validated by comparing the results of our calculations, to those obtained from experimental studies, figure 4 shows that the agreement between the predictions and experiment appears to be satisfactory, the influence of inclination angle on the thermal performance of the device has been discussed.It is proved by the results that Runge Kutta method can be used effectively for such predictions. The suggested methodology can be used to model systems, which are difficult to model analytically. CPC reflectors provide effective solar radiation concentration, depending on their acceptance angle. The results showed that the ICS systems with CPC reflectors achieve higher water temperature rise during the day, but also higher thermal losses during the night.
Nomenclature


References
| [1] | M. Souliotis, Y. Tripanagnostopoulos, Study of the distribution of the absorbed solar radiation on the performance of a CPC-type ICS water heater, Renewable Energy 33 (2008), 846 - 858. |
| [2] | Y. Tripanagnostopoulos, M. Souliotis and TH. Nousia, CPC type integrated collector storage systems, Solar Energy, vol. 72 (2002), N. 4, 327 - 350. |
| [3] | M. Smyth, P.C. Eames, B. Norton, Techno-economic appraisal of an integrated collector/storage solar water heater, Renewable Energy, 29 (2004), 1503 - 1514. |
| [4] | F. Fooladi, H. Taherian, Experimental study of a multi-tube ICS solar water heating system in mild climates, Applied Solar Energy, vol. 46 (1), pp. 22 - 31, 2010. |
| [5] | M. Souliotis, Y. Tripanagnostopoulos, Experimental study of CPC type ICS solar systems, Solar Energy, 76 (2004) 389 - 408. |
| [6] | M. Souliotis, S. Kalogirou, Y. Tripanagnostopoulos, Modelling of an ICS solar water heater using artificial neural networks and TRNSYS, Renewable Energy 34 (2009) 1333 - 1339. |
| [7] | J. M. Chasseriaux, Convection Thermique et Rayonnement Solaire. ed. dunod, 1984. |
| [8] | H. P. Garg, Advances in solar energy technologie, Kluwer academic publishers, 1987. |
| [9] | J. A. Duffie, W. A. Beckman, Solar energy thermal processes, 2nd ed. Wiley Interscience, New York, USA, 1974. |
| [10] | Jannot Y., Thermique solaire, p 111, 2007; site: www. thermique55.com/principal/thermique.pdf |
| [11] | K. Gairaa, Y. Bakelli, An overview of global solar radiation measurements in Ghardaïa area, south Algeria, international journal of energy and environment, Volume 2, Issue 2,(2011) pp.255-260. |
| [12] | S.M.A. Bekkouche, T. Benouaz, A. Cheknane, A modelling approach of thermal insulation applied to a Saharan building, Thermal Science 13 (4) (2009) 233–244. |
| [13] | M.R. Yaïche et, S.M.A. Bekkouche, Conception et validation d’un programme sous Excel pour l’estimation du rayonnement solaire incident en Algérie, cas d’un ciel totalement clair, Revue des Energies Renouvelables 11 (3) (2008) 423-436. |
| [14] | M.R. Yaïche et, S.M.A. Bekkouche, Conception et validation d’un programme sous Excel pour la modélisation d’une station radiométrique en Algérie, cas d’un ciel totalement clair, Revue des Energies Renouvelables 12 (N◦4) (2009) 677–688. |
| [15] | M. Capderou, Modèles théoriques et expérimentaux, Atlas solaire de l’Algérie, Office des Publications Universitaires, Algérie, Tome 1 Vol 1 et 2, 1987. |
| [16] | A. Mefti, M.Y. Bouroubi et, A. Khellaf, Analyse critique du modèle de l’atlas solaire de l’Algérie, Revue des Energies Renouvelables 2 (2) (1999) 69–85. |
| [17] | F. Kasten, A.T. Young, Revised optical air mass tables and approximation formula, Applied Optics 28 (22) (1989) 4735–4738. |
| [18] | F. Kasten, A simple parameterization of two pyrheliometric formulae for determining the Linke turbidity factor, Meteorology Rdsch 33 (1980) 124–127. |
| [19] | F. Kasten, The Linke turbidity factor based on improved values of the integral Rayleigh optical thickness, Solar Energy 56 (3) (1996) 239–244. |


 .n : representing an average number of reflections for a CPC. θc : represents the acceptance angle.The prototype geometrical dimensions are length L and width 2W.
.n : representing an average number of reflections for a CPC. θc : represents the acceptance angle.The prototype geometrical dimensions are length L and width 2W.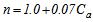
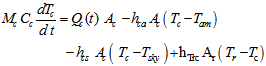
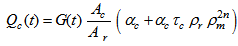
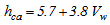
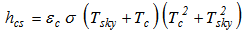
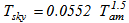
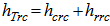
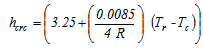
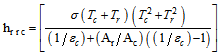
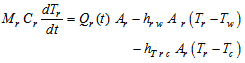
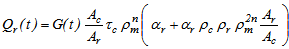
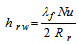
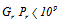
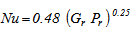
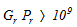
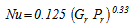
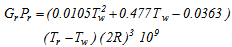
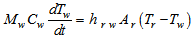






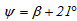





 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML