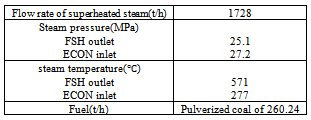
-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Energy Engineering
p-ISSN: 2163-1891 e-ISSN: 2163-1905
2012; 2(5): 210-217
doi: 10.5923/j.ijee.20120205.04
Study of a Multivariable Coordinate Control for a Supercritical Power Plant Process
Omar Mohamed 1, Jihong Wang 2, Bushra Al-Duri 3, Junfu Lu 4, Qirui Gao 4, Yali Xue 4
1School of Electronic, Electrical and Computer Engineering, University of Birmingham, B15 2TT, UK
2School of Engineering, University of Warwick, Coventry CV4 7AL, UK
3School Chemical Engineering, University of Birmingham, B15 2TT, UK
4Department of Thermal Engineering, Tsinghua University, Beijing, 100084, China
Correspondence to: Omar Mohamed , School of Electronic, Electrical and Computer Engineering, University of Birmingham, B15 2TT, UK.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
the paper presents our recent research work in study of a novel multivariable coordinate control for a 600MW supercritical (SC) power plant process. The nonlinear mathematical model of the plant is briefly described in the paper. Then, a control strategy is designed which is based on Generalized Model Predictive Control (MPC) theory and tested within small load changes. But the MPC alone performs well only within small load changes even with consideration of constant disturbance and measurement noises in prediction algorithm. We then propose a dynamic compensator in parallel with the MPC to track large load changes. Because the model has been identified with on-site closed loop data, the multivariable optimal control signals have been used as a correction to the reference of the plant local controls instead of direct control signal applications. The simulation results have shown good performance of the controller in response to some load changes. Furthermore, it has been proved that the plant dynamic response can be improved by increasing the coal grinding capability and pulverized coal discharging through the implemented coal mill controllers. The benefit from this study is to provide convinced methodology to improve the SC power plant dynamic response for fulfilment of National Grid Code (NGC) requirements.
Keywords: Supercritical Power Plant; Mathematical Modelling , Optimal Control of Chemical Process
Article Outline
1. Introduction
- Although there is a considerable renewable energy penetration to electrical power supply in recent years, coal fired power stations are still playing a dominant role in power generation due to its large power generation capacities and low cost. It is a worldwide big challenge for how to reduce the environmental impact brought from coal fired power generation. Supercritical boiler is one of the technologies implemented with the improved energy efficiency. Supercritical boilers have higher efficient Ranking cycle due to its high operating pressure and temperature (above critical points - for water 22.06MPa and 374.15C° pressure and temperature respectively), leading to improved thermal efficiency, lower fuel consumption and lower CO2 emissions. Although supercritical and ultra-supercritical coal fired power generation is becoming the main choice of power generation technology for past two decades and will become a dominant technology on the long run, there are still some concerns about adopting this technology in the UK. It is required to fulfil the National Grid Code (NGC) require ments[1]. The paper is to study potential control strategies for improving SC power plant dynamic responses. The first research on optimal control of SC power plants was designed in 1978([2]) with identified state space model and dynamic programming for control task formulation. The application of nonlinear model based predictive control (NMBPC) was reported in[3] as preliminary results. Conventional dynamic matrix control (DMC) was published in[4] designed for gas fired SC power plants. However, conventional DMC may not cover the whole operating range. In[5], a simplified model for SC unit was reported for power system frequency simulation study. The performance of diagonal recurrent neural network for predictive control of coal fired SC and ultra-supercritical (USC) power plants were shown in[6-8]. This paper aims to design coordinated control system for 600MW SC coal fired plant with emphasis on the target of correcting the reference of plant local controllers. Because the model has been identified with closed loop data, the designed control signals should be used as correction to the reference of the plant local controls (the coal mill local control, the feed-water flow control, and the turbine governing system) which is extremely helpful in power plant industries. Two coordinated controllers are investigated. One is based on MPC with disturbance compensation and measurement noises generalized from prediction algorithm. This scheme has shown good performance within small load changes around nominal operating conditions. The other scheme is multivariable control system which is composed of MPC in parallel cooperation with PID fully coupled structure compensator. The use of dynamic compensator as additional means to track large steps of load changes for more reliable of power plant operation. By this, two features will be covered in handling the constraints and robust performance. Simulation results have shown the applicability of the proposed idea. It has been also proved that the coal mill local control of feeder speed and primary air fans have significant on the plant primary response of MW power output.
2. Description of the Plant Process
|
3. The Process Mathematical Model
3.1. Model Description
- The power plant process is illustrated in Figure. 1. It is a complex system with multi interconnection of subsystems and components. The first task for our study is to derive the mathematical model for the process. The detailed modelling study can be found in the previous work of the authors[9-12]. The parameters, detailed model structure and the way how if is derived are all described in those references. The variables appear in Figure.1 are defined in Table.2.The coal mill model described in[9,10] is integrated with the rest of the plant model reported in[11,12]. Because there are multiple mills operating in parallel in real power plants, a proportional gain is multiplied by the pulverized coal output to account the total pulverized coal supplied to the burners. The heat flow is basically related to fuel flow through proportional gains (Ke, Kww, Ksh, and Krh) as shown in the figure with 1st order lag transfer function. For more details about modelling, please refer to[11, 12].
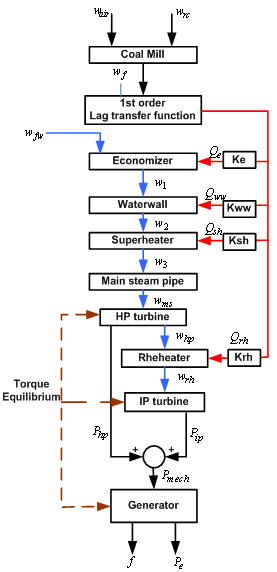 | Figure 1. Illustration of a SC power plant process mathematical model |
|
3.2. Computer Implementation and Parameter Identification
 | Figure 2. Mass flow(Kg/s) Data set.1(identification) |
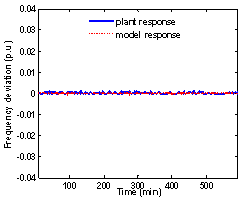 | Figure 3. Frequency Deviation(identification) |
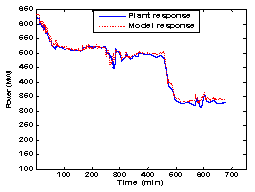 | Figure 4. Electrical Power Data set.2 (verification) |
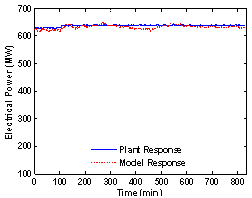 | Figure 5. Electrical Power Data set.3(verification) |
 | Figure 6. Main Steam pressure Data set.3(verification) |
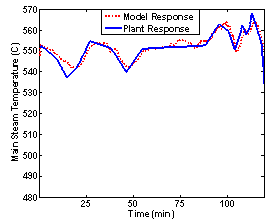 | Figure 7. Main Steam temperature Data set.4(verification) |
4. Generalized Predictive ControllerSet-up
- A model based predictive control is developed with provisions of unmeasured disturbances and measurement noises to be used for compensation around the investigated operating conditions. Here, the linear time invariant model is used for the MPC algorithm while the process mathematical model has been used to simulate the power plant responses. GA has been used again to develop the internal model of the MPC which initially has the following form:
 | (1) |
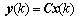 | (2) |
 ,The inputs and the outputs which have been used for identification of the controlled plant are chosen as:
,The inputs and the outputs which have been used for identification of the controlled plant are chosen as:
4.1. The Generalized Predictive controller
- In this research, the generalized predictive controller algorithm described in[14] is adopted which has been widely used for chemical or thermodynamic process control[14-17]. The prediction model has been upgraded as follows:
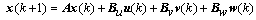 | (3) |
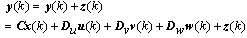 | (4) |
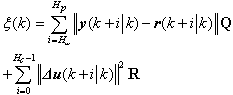 | (5) |
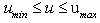 | (6) |
 | (7) |
 Subject to (6) and (7).
Subject to (6) and (7).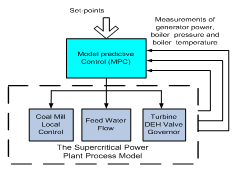 | Figure 8. Generalized Predictive controller scheme |
4.2. Simulation Study 1 (small load change)
- The results are mentioned in figures 9.10.11. Case.A represents the improved case with embedded plant controllers while Case.B represents the existing milling and plant performance. It is clearly seen that the control strategy speeds-up the plant power primary response with significant improvements. Furthermore, the boiler pressure and temperature respond with less fluctuation and are kept within supercritical conditions to ensure optimal efficiency despite load variation. In figure 11, the various mill variables are presented. It seems that the mill should draw higher current than normal case in order to provide better grinding capability. In addition, higher differential pressure of the mill and primary air pressure are created to carry more pulverized coal to the furnace. In the next section, the plant will be equipped with robust compensator and tested with large load changes.
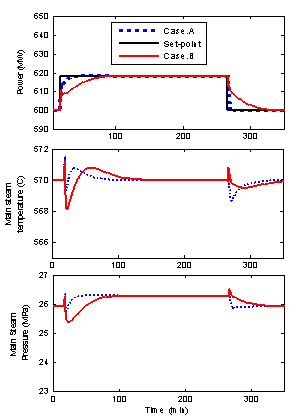 | Figure 9. Controlled variables of the SC Power Plant |
 | Figure 10. Input variables to the boiler-turbine-generator system |
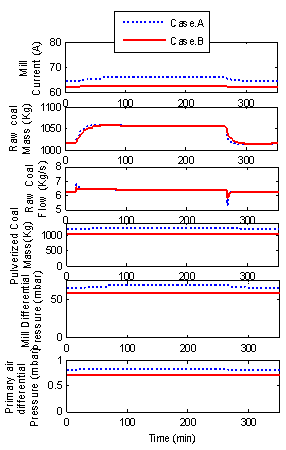 | Figure 11. Variables of each mill in service |
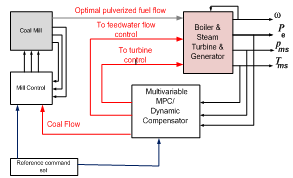
5. The MIMO Compensator Design and Incorporation
- The plant model embeds high nonlinear features. The MPC performs well on small load change even with consideration of constant disturbance and measurement noises in prediction. The performance of MPC alone for large load change or partial load rejections was totally unacceptable. The MIMO compensator is designed by using Genetic Algorithms. This compensator has no function except compensating control errors resulting form large load changes. It has been located in parallel with the MPC. The procedures are given in the next section.
5.1. MIMO compensator design
- The parallel structure MIMO PID with coupled structure can be designed and reported in many research articles[19-21], the generalized form for n×n system is then described by:
 | (8) |
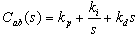 | (9) |
 | (10) |
|
 | Figure 12. Multivariable controller scheme |
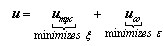 where e is the error remaining from plant severe nonlinearity and the subscripts to indicate the outputs responses of pressure, Power, and Temperature, respectively. w1, w2 , w3 are the weighting coefficients used in optimization. In our work, the matrix K is only 3×3 matrix. The major steps performed by GA to reach the optimal solution can be found in[13]. The dynamic compensator parameters are listed in Table.3. The additional corrections to the MPC control signals are introduced to simulate large load event (See figure.12).
where e is the error remaining from plant severe nonlinearity and the subscripts to indicate the outputs responses of pressure, Power, and Temperature, respectively. w1, w2 , w3 are the weighting coefficients used in optimization. In our work, the matrix K is only 3×3 matrix. The major steps performed by GA to reach the optimal solution can be found in[13]. The dynamic compensator parameters are listed in Table.3. The additional corrections to the MPC control signals are introduced to simulate large load event (See figure.12).5.2. Simulation study 2 (Large load changes)
- Simulation results are mentioned in the same two cases in section 5.1 to show the performance of the control strategy proposed including the effect of milling dynamics. Again the improvements in the primary response of the plant power can be seen even with large load variation. Then, this configuration merits application on SC power plant to improve its dynamic response with emphasis on the issue of National Grid Code compliance.There are other parallel schemes reported in the literature of chemical process control[22, 23]. In[22], an adaptive neuro controller is located in parallel with MPC to increase the controller robustness while in[23] extra PID scheduled loops are installed in parallel with MPC to compensating the plant nonlinearity. The slow dynamics of the mill can be handled by its local control system.
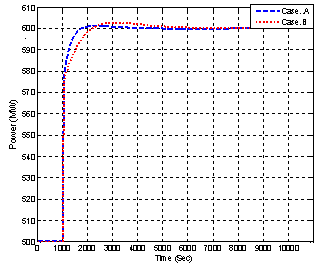 | Figure 13. Electrical power dynamic response |
 | Figure 14. Pressure and Temperature |
 | Figure 15. Manipulated Variables |
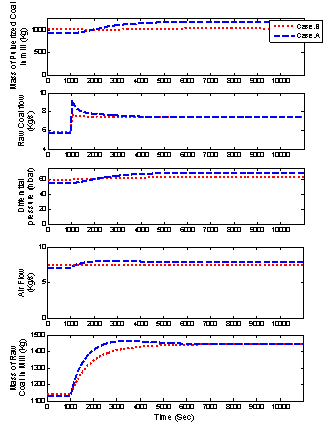 | Figure 16. Variables for each mill in service |
6. Conclusions
- A mathematical model of a coal fired supercritical power plant is described in the paper. Simulation study indicates the model can predict the main dynamic response variation trends of the 600MW SC power plant process. A coordinate control is proposed and tested through simulation study with relatively large load changes. The control considers the milling process as a key stage for power plant dynamic response improvement. From the study, it is convinced that better control of the milling process can improve the power plant load following capability and/or primary response of the plant power. As future recommendations, more accurate and detailed models will be developed to simulate SC power plant and Ultra-supercritical (USC) power plants for more complicated studies.
ACKNOWLEDGEMENTS
- The work of the paper was supported in part by UK EPSRC grant (EP/G062889/1) and AWM/ERDF Birmingham Science City Energy Efficiency and Demand Reduction project.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML