-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Energy Engineering
p-ISSN: 2163-1891 e-ISSN: 2163-1905
2012; 2(5): 184-194
doi: 10.5923/j.ijee.20120205.01
An Overview on Application of Exergy and Energy for Determination of Solar Drying Efficiency
Lyes Bennamoun
Department of Applied Chemistry, University of Liège, Sart Tilman Bât. 6c, Liège, 4000, Belgium
Correspondence to: Lyes Bennamoun , Department of Applied Chemistry, University of Liège, Sart Tilman Bât. 6c, Liège, 4000, Belgium.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
The main objective of this work is to give an overview of the different used mathematical methods for modeling and calculating the energy and exergy efficiency of a solar drying system. For determination of the energy efficiency of thin or thick layers, heat and mass balances are established to the different components. In the case of thick layers equations of porous media are used. These methods allow following, in particular, the variations of the heated air and the product temperature and humidity. As a second part, the common way for the calculus of the exergetic efficiency passes through the establishment of exergy balance and after calculating the input, output and exergy loss. The influence and illustration of several parameters are as well presented in this paper.
Keywords: Solar Air Collector, Drying Chamber, Energetic Efficiency, Exergy Efficiency, Mathematical Modelling
Article Outline
1. Introduction
- Drying constitutes an important process for a large variety of industries. For example, for foodstuffs, it is a necessary step for the preservation of the final product or to make it ready to be stored[1-4]. On the other hand and for other materials, such as woods, concretes, bricks and sludge, the passage by this process is an obligation to make these products marketable[5-8]. As it is well known, drying is the most energy intensive operation of the industrial processes. In most industrialized countries, between 7 and 15% of a nation’s industrial energy is used for drying[9]. Other estimations report that national energy consumption for industrial drying operations are ranging from 10 to 15% for United States, Canada, France and United Kingdom and reach 20 to 25% for Denmark and Germany[10]. Furthermore, around 35 % of the consumed energy in drying is used for paper and pulp industry and only 5% are used for chemicals[10]. The resulted high cost of this unit operation directed the efforts of the Scientifics to look for alternative cheap sources of energy, in particular free solar energy. Coupling the two ideas gives birth to several types of solar dryers. In general manner, solar dryers are classified into active and passive dryers and each classification is divided into direct, indirect and mixed mode type[11-13]. However and in order to face the intermittent character of solar energy, developed systems can be dotted with a second source of energy using electrical heater[1, 14] or storage systemsfilled with packed rock-beds[15-17], gravels[18], desiccants[19], water[20] or phase change material[21-23]. We cannot have an optimum use and design of a solar dryer without passing through simulation and the mathematical modelling. The existing models are taking essentially two ways: the first approach studies particularly the behaviour of the product during the process represented by the drying kinetic. These developed models agree to calculate several parameters such as coefficient of diffusion, heat and mass coefficients and drying constants[5, 24-35]. The second approach studies the general behaviour of the solar dryer by applying heat and mass transfers. It allows following variations of temperature and humidity of both the dried product and the heated air. But also it permits following the different temperatures and other parameters of the solar collector and the drying chamber. By this method, efficiency of the studied system can be easily obtained. In this paper, we are focusing on this second approach.In this last decade, exergy is introduced as an important and a powerful analysis tool for design and calculus of the performances of thermal systems. From a thermodynamic point of view, exergy is defined as the maximum amount of work which can be produced by a quantity or flow of matter, heat or work as it comes to equilibrium with a reference environment[36]. Exergy starts finding applications in several industries and we direct our attention to the application for drying process[37-44].Therefore, the aim of this paper is to present a review about the application of exergy and energy to solar drying with presentation of the different mathematical models that treat the general behaviour of the drying systems and calculate their energetic and exergetic efficiencies with products packed in thin or thick layers.
2. Energy Analysis
2.1. Solar Drying of Thin Layers
- We will apply our study to a representative simple convective solar dryer, represented in Figure 1a. It is constituted of two parts; a simple flat solar air collector (Figure 1b). It is composed of an aluminium plate used as an absorber, covered from the above by a glass plate and insulated from the exterior using polystyrene. There is a vacuum space between the absorber and the glass cover. The second part concerns the drying chamber made with bricks insulated from the exterior by polystyrene and can support trays where the product is putted. Forced convection is obtained using a fan which permits to have a homogeneous distribution of the heated air inside the drying chamber; also it allows having better control of the process[1, 11].One of the frequent models used to study solar drying of thin layers (putted in perforated trays), is: step by step method[1, 13, 45]. It consists on taking a fictitious slice that can be noted “j”, applying heat and mass balance to this slice, then generalizing the study to all the system by varying the step “j”. This method is applied to both the solar collector (Figure 1b) and the drying chamber (Figure 2).
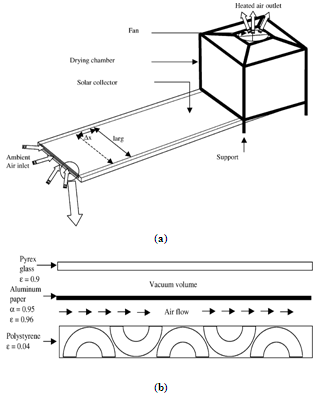 | Figure 1. (a) Global diagram of a solar dryer. (b) Step “j” of the flat plate solar air collector[1] |
2.1.1. Application to the Solar Collector
- A heat balance is established for the different components; which are the interior and exterior side of the glass cover, the absorber, the interior and exterior side of the insulator, resumed by Equation 1 and Table 1:
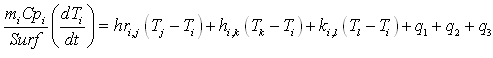 | (1) |
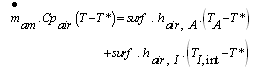 | (2) |
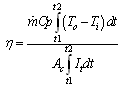 | (3) |
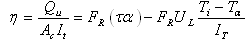 | (4) |
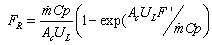 | (5) |
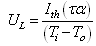 | (6) |
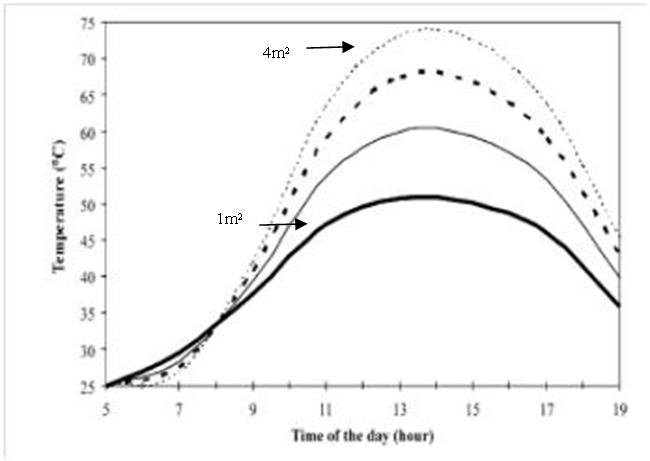 | Figure 2. Influence of the surface of the collector on its outlet air temperature[1] |
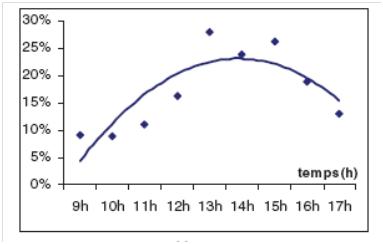 | Figure 3. Variation of the efficiency of a solar collector with time[48] |
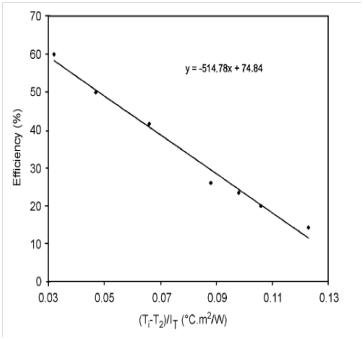 | Figure 4. Collector efficiency with (Ti-Ta)/IT[46] |
2.1.2. Application to the Drying Chamber
- A step ``j`` of the drying chamber is shown in Figure 5.
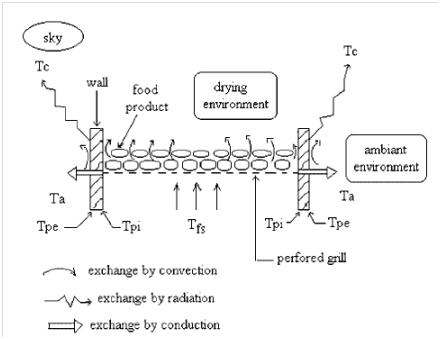 | Figure 5. Step “j” of the drying chamber[50] |
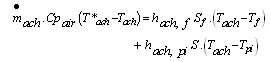 | (7) |
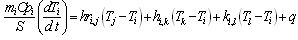 | (8) |
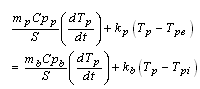 | (9) |
|
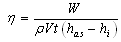 | (10) |
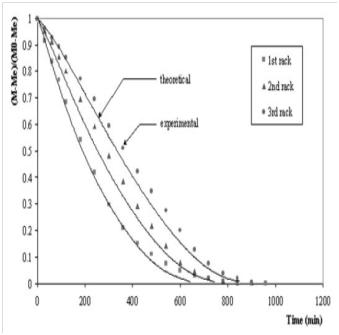 | Figure 6. Evolution of the reduced content in three racks[50] |
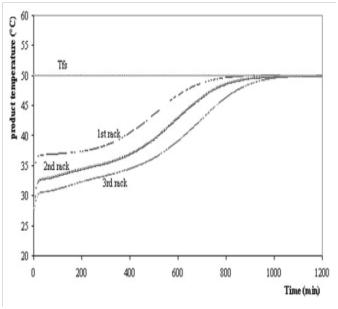 | Figure 7. Product temperature profile[50] |
2.2. Solar Drying of Thick Layers
- The unique difference between solar drying of thin and thick layers is that, for the second case, the product is filled in multiple condensed layers. However, it does not affect the precedent study relative with the solar collector and the same mathematical procedure is used.As the product is filled in thick layers, the drying chamber can be supposed as a porous media in the macroscopic scale. So, mathematical model describing transfer in porous media can be applied for the product, represented by the solid phase, and the heated air, presented as the gas phase. We obtain four differential equations[4, 13, 51].Application of mass balance in gas phase:
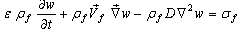 | (11) |
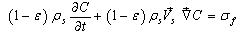 | (12) |
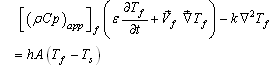 | (13) |
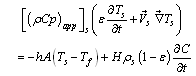 | (14) |
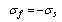 | (15) |
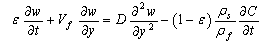 | (16) |
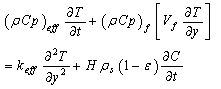 | (17) |
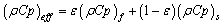 | (18) |
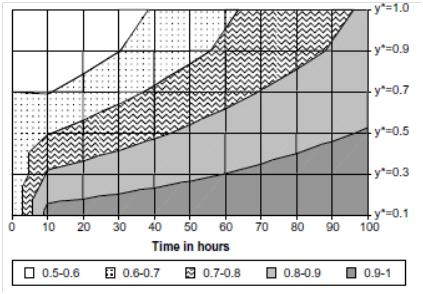 | Figure 8. Variation of the temperature of the media vs. time and bed deep[51] |
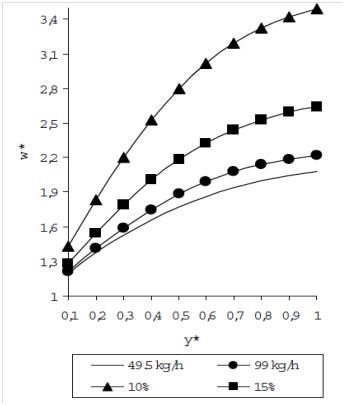 | Figure 9. Influence of flow rate and initial humidity on humidity of the heated air[54] |
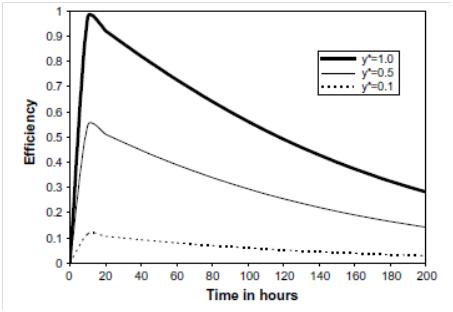 | Figure 10. Variation of the pick-up efficiency during drying of thick layers[51] |
2.3. System Efficiency
- The system efficiency indicates the overall thermal performance of a drying system including the efficiency of a solar collector, the drying chamber and any other supplement add to the system. The global efficiency is written[52]:For natural convection solar dryers:
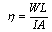 | (19) |
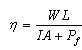 | (20) |
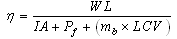 | (21) |
3. Exergy Analysis
- Exergy is presented as a useful analysis tool in the design, assessment, optimization and improvement of energy systems, that can be applied on both system and components levels[55-56]. The exergy method can help further the goal of more efficient energy resource use, because it enables the locations, types and true magnitudes of looses to be determined. As a result, exergy analysis can reveal where and by how much it is possible to design more efficient thermal systems by reducing the sources of existing inefficiencies[49].The second law of thermodynamics introduces the useful concept of exergy in the analysis of thermal systems. Exergy analysis evaluates the available energy at different points in a system. Exergy is a measure of the quality of grade of energy and it can be destroyed in the thermal system. The second law states that part of the exergy entering a thermal system with fuel, electricity, flowing streams of matter, and so on is destroyed within the system due to irreversibility. The second law of thermodynamics uses an exergy balance for the analysis and the design of thermal systems[49].The general mathematical description of the exergy is presented under the following equation[48-49, 57-59]:
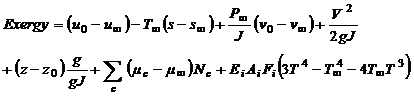 | (22) |
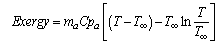 | (23) |
3.1. Application of Exergy for Solar Collector
- The most presented papers, dealing with exergy analysis of solar drying, are presenting solar dryers similar to one illustrated in Figure 1. The drying system contains a simple solar air heater, and a drying chamber that supports horizontal trays. The system can work with natural convection (without fan) or using forced convection (with fan).In the case of application of exergy to a simple solar air collector; the terms of momentum, gravity and chemical reaction can be neglected. However, radiation emission term that depends on temperature must be kept.The exegy loss is the difference between the exergy inlet and outlet that are respectively functions of the inlet and outlet temperatures. It is expressed:Exergy loss = Exergy inflow-exergy outflowMathematically determined by equation 24:
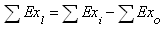 | (24) |
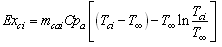 | (25) |
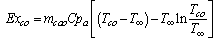 | (26) |
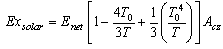 | (27) |
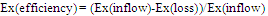 | (28) |
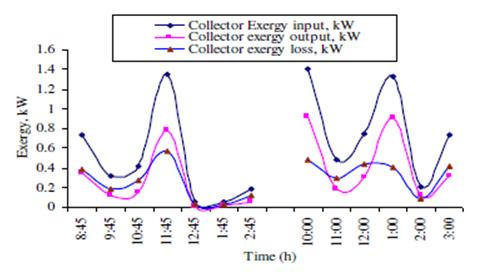 | Figure 11. Variation of the collector exergy parameters with drying time[49] |
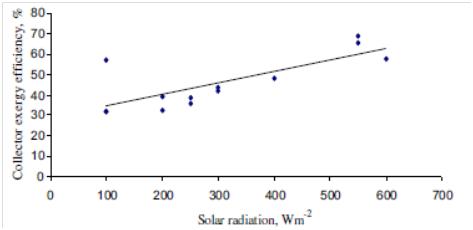 | Figure 12. Variation of the collector exergy efficiency parameters with solar radiation[49] |
3.2. Application of Exergy to the Drying Chamber
- Based on the same way, a comprehensive procedure of the application of exergy for the drying chamber was developed[36, 60-61]. A representative scheme is illustrated in Figure 13.
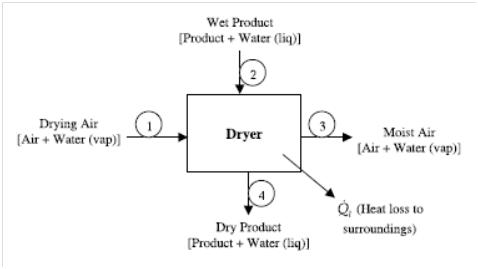 | Figure 13. Schematic of a drying process showing input and output terms for the drying chamber[60-61] Exergy balance gives[60-61]: |
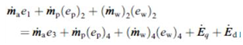 | (29) |
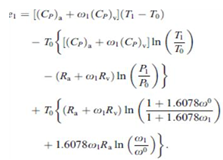 | (30) |
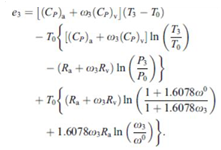 | (31) |
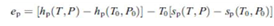 | (32) |
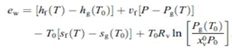 | (33) |
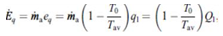 | (34) |
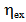 = Exergy for evaporation of moisture in product / Exergy of drying air suppliedOr mathematically:
= Exergy for evaporation of moisture in product / Exergy of drying air suppliedOr mathematically: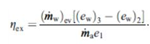 | (35) |
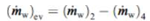 | (36) |
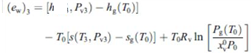 | (37) |
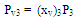 | (38) |
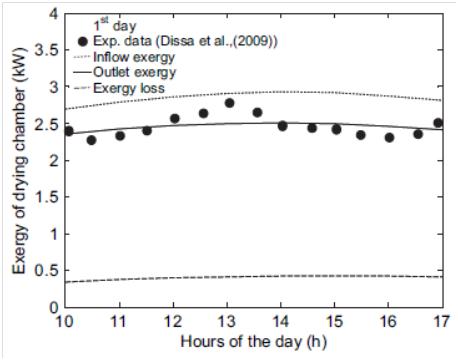 | Figure 14. Variation of the drying chamber exergy as a function of the drying time[59] |
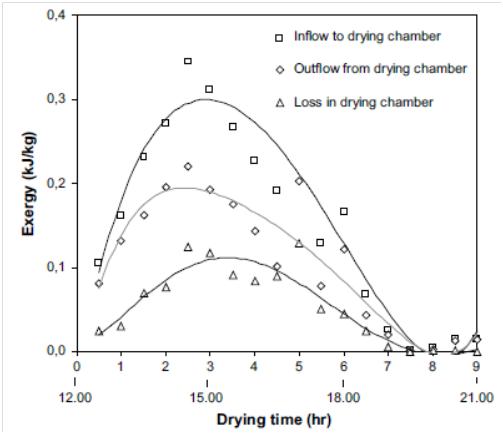 | Figure 15. Variation of different exergy parameters inside the drying chamber[58] |
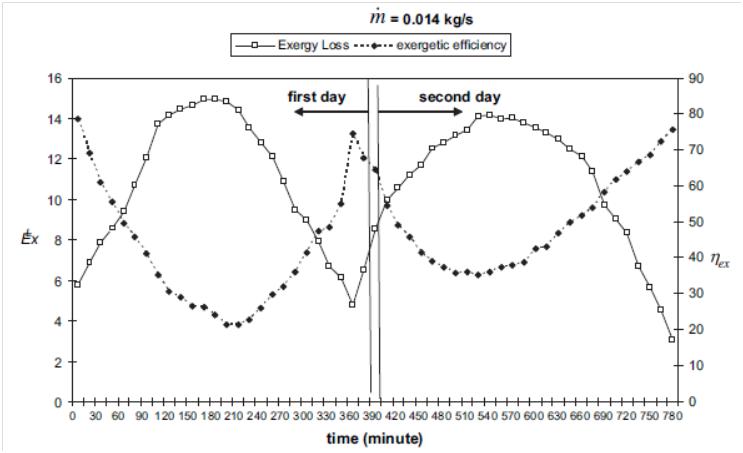 | Figure 16. Variation of total exergy loss and total exergetic efficiency of a solar dryer[63] |
3.3. Calculation of the System Exergy Efficiency
- It is determined by:
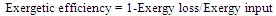 | (39) |
4. Conclusions
- Simulation and mathematical modelling plays an important role for the design of a solar drying system. To have an idea about the general behaviour of a solar drying system and to be able to calculate its energetic efficiency; it is important to establish heat and mass balance. This method is then applied for the different components of the drying system, which means both the solar collector and the drying chamber. It allows following the variation, in time and space, of different temperatures and parameters in particular temperature and humidity of the dried product and the heated air, necessary for the calculation of the energetic efficiency. For thick layers drying, the drying chamber is considered as a porous media and then mathematical treatment by using transfers in porous media can be done. Also, this method gives the variations of the air and product temperatures and humidity, permitting the calculation of the energetic efficiency for this case, too.A detailed mathematical procedure to be adopted for calculation of the exergetic efficiency is proposed with application to a solar collector, to the drying chamber and the overall solar drying system. This mathematical procedure can be applied for both thin and thick layers. Exergetic efficiency can then be easily calculated by knowing some accessible parameters such as temperatures and humidity.By means of the presented results, it is clear that the calculated efficiencies are deeply influenced by several parameters such as the variation of the received radiation, the external temperature and the wind velocity during drying time, by internal parameters and the design such as the surface of the solar collector, by the characteristics of the dried product. So, an optimum exploitation of the studied system with a minimum of expenses passes through simulating and modelling, in particular with calculation of energetic and exergetic efficiencies.
Nomenclature
- Cp→specific heat (J/kg.K)ṁ→mass flow rate (kg/s)T→temperature (K)t→time (s)Section 2A→surface of the collector (m2)FR→heat removal factor of solar collectorF’→collector efficiency factorh→coefficient of heat transfer by convection (W/m2.K)hr→adapted radiative exchange coefficient (W/m2.K)I, It→Incident radiation (W/m2)k→adapted conductive exchange coefficient (W/m2.K) LCV→lower calorific value of fuel (J/kg)L→latent heat of vaporization of water (J/kg)m→mass (kg)mb→mass of fuel consumed (kg)Pf→energy consumption of fan/blower (J)Qu→useful energy gain of collector (W/m2)q→energy term (W/m2)surf→surface (m2)S→surface of wall dryer (m2)UL→global heat loss coefficient (W/(m2.K)V→volumetric air flow (m3/s)W→weight of water evaporated from the product (kg)*→precedent traySubscriptsach→heated airA→absorberam→ambient airb→brick wallc→collectorfld→fluid (air)f→productI→insulatorint→interior sidei→inputi –l→Indices (reference table 1 or table 2)o→outputp→insulatorpe→exterior face of the insulatorpi→interior face of the insulatorth→theoreticalGreek symbolsα→absorption coefficientη→energetic efficiencyρ→density (kg/m3)τ→transmission coefficientSection 2.2A→surface of contact air-product (m2)C→moisture content of the product (kg/kg)D→coefficient of diffusion (m2/s)H→latent heat of vaporization of water (J/kg)V→velocity (m/s)w→humidity ratio (kg/kg)y→coordinate (m)Subscriptseff→effectivef→fluids→solid (dried product)Greek symbolsε→bed porosityσ→mass transfer factor (kg/m3s)Section 3Ai→inlet area (m2)Ei→emissive power at inlet (W/m2)Ex→exergy (J)Ė→rate of energy flowe→specific exergyFi→inlet shape factorg→Gravitational acceleration (m/s2)h→specific enthalpyJ→Joule constantma→mass flow rate of air (kg/s)Nc→number of speciesP→pressure (Pa)Q→rate of heat transferR→Gas constants→specific entropy (j/kg.K)u→specific internal energy (J/s)v→specific volume (m3/kg)V→velocity (m/s)xv→mole fraction of vaporz→altitude coordinate (m)Subscriptsa→airc→collectord→destructionexvrelated to exergyg→saturated vapour statei→inletl→losso→outletp→productq→heat transfer relatedv→vaporw→water∞→ambient0→dead stateGreek symbolsμ→chemical potential (J/kg)ω→humidity ratio of airω0→humidity ratio of air at dead state
References
| [1] | Bennamoun, L., Belhamri, A., 2003, Design and simulation of a solar dryer for agriculture products, Journal of Food Engineering, 59 (2-3), 259–266. |
| [2] | Gallali, Y. M., Abujnah, Y.S., Bannani F. K., 2000, Preservation of fruits and vegetables using solar drier: a comparative study of natural and solar drying III; chemical analysis and sensory evaluation data of the dried samples (grapes, figs, tomatoes and onions), Renewable Energy, 19(1-2), 203-212. |
| [3] | Srivastava, V. K., John, J., 2002, Deep bed drying modeling, Energy Conversion & Management, 43 (13), 1689-1708. |
| [4] | Arnaud, G., Fohr, J. P., 1988, Slow drying simulation in thick layers of granular products, International Journal of Heat and Mass Transfer, 31 (12), 2517-2526. |
| [5] | Bennamoun, L., Belhamri, A., Ali-Mohamed, A., 2009, Application of a diffusion to predict drying kinetics changes under variable conditions: Experimental and simulation study, Fluid Dynamics & Materials Processing, 5(2), 177-191. |
| [6] | Chen, P., Pei, D. C. T., 1989, A mathematical model of drying processes, International Journal of Heat and Mass Transfer, 32 (2), 297-310. |
| [7] | Huang, C. L. D., Siang, H. H., Best C. H., 1979, Heat and moisture transfer in concrete slabs, International Journal of Heat and Mass Transfer, 22 (2), 257-266. |
| [8] | Bennamoun, L., 2012, Solar drying of wastewater sludge: A review, Renewable and Sustainable Energy Reviews, 16 (1), 1061-1073. |
| [9] | Keey, R. B., 1992, Drying of loose and particulate materials, Hemisphere Publishing Corporation, U.S.A. |
| [10] | Mujumdar, A. S., 2006, Principles, classification, and selection of dryers, Handbook of industrial drying, Mujumdar A.S., Ed. U.S.A: CRC press. |
| [11] | Bennamoun, L., 2011, Reviewing the experience of solar drying in Algeria with presentation of the different aspects of solar dryers, Renewable and Sustainable Energy Reviews, 15 (7), 3371-3379. |
| [12] | Eckchukwu, O. V., Norton, B., 1999, Review of solr-energy drying systems II: an overview of solar drying technology, Energy Conversion & Management, 40 (6), 615-655. |
| [13] | Daguenet, M., 1985, Les séchoirs solaires: théorie et pratique, UNESCO, Paris. |
| [14] | Boughali, S., Benmoussa, H., Bouchekima, B., Mennouche, D., Bouguettaia, H., Bechki, D., 2009, Crop drying by indirect active hybrid solar-Electrical dryer in the eastern Algerian Septentrional Sahara, Solar Energy, 83 (12), 2223-2232. |
| [15] | Jain, D., 2007, Modeling the performance of the reversed absorber with packed bed thermal storage natural convection solar crop dryer, Journal of Food Engineering, 78 (2), 637-647. |
| [16] | Jain, D., Jain, R. K., 2004, Performance evaluation of an inclined multi-pass solar air heater with in-built thermal storage on deep-bed drying application, Journal of Food Engineering, 65 (4), 497-509. |
| [17] | Chauhan, P. M., Choudhury, C., Garg, H. P., 1996, Comparative performance of coriander dryer coupled to solar air heater and solar air-heater-cum-rockbed storage, Applied Thermal Engineering, 16 (6), 475-486. |
| [18] | Mohanraj, M., Chandrasekar, P., 2009, Performance of a forced convection solar drier intergrated with gravel as heat storage material for chilli drying, Journal of Engineering Science and Technology, 4 (3), 305-314. |
| [19] | Shanmugam, V., Natarajan, E., 2006, Experimental investigation of forced convection and desiccant integrated solar dryer, Renewable Energy, 31 (8), 1239-1251. |
| [20] | Luna, D., Nadeau, J. P., Jannot, Y., 2010, Model and simulation of a solar kiln with energy storage, Renewable Energy, 35 (11), 2533-2542. |
| [21] | Devahastin, S., Pitaksuriyarat, S., 2006, Use of latent heat storage to converse energy during drying and its effect on drying kinetics of a food product, Applied Thermal Engineering, 26(14-15), 1705-1713. |
| [22] | Bal, L. M., Sudhakar, P., Satya, S., Naik, S. N., 2009, Solar dryer with latent heat storage systems for drying agricultural food products, in Proceedings of International Conference of Food Security and Environmental Sustainability. |
| [23] | Al-Hamadani, A. A. F., Shukla, S. K., 2011, Water Distillation using solar energy system with lauric acid as storage medium, International Journal of Energy Engineering, 1(1), 1-8. |
| [24] | Tripathy, P. P., Kumar, S., 2009, A methodology for determination of temperature dependent mass transfer coefficients from drying kinetics: Application to solar drying, Journal of Food Engineering, 90 (2), 212-218. |
| [25] | Boubekri, A., Benmoussa, H., Mennouche, D., 2009, Solar drying kinetics of date palm fruits assuming a step-wise air temperature change, Journal of Engineering Science and Technology, 4 (3), 292-304. |
| [26] | Doymaz, I., 2005, Sun drying of figs: an experimental study, Journal of Food Engineering, 71 (4), 403-407. |
| [27] | Toğrul, I. T., Pehlivan, D., 2004, Modelling of thin layer drying kinetics of some fruits under open-air sun drying process, Journal of Food Engineering, 65 (3), 413-425. |
| [28] | Toğrul, I. T., Pehlivan, D., 2003, Modelling of drying kinetics of some single apricot, Journal of Food Engineering, 58 (1), 23-32. |
| [29] | Midilli, A., Kucuk, H., Yapar, Z., 2002, A new model for single-layer drying, Drying technology, 20 (7), 1503-1513. |
| [30] | El Sebaii, A. A., Aboul-Enein, S., Ramadan, M. R. I., El-Gohary, H. G., 2002, Empirical correlations for drying kinetics of some fruits and vegetables, Energy, 27 (9), 845-859. |
| [31] | Toğrul, I. T., Pehlivan, D., 2003, Mathematical modelling of solar drying of apricots in thin layers, Journal of Food Engineering, 55 (3), 209-216. |
| [32] | Yaldiz, O., Ertekin, C., Uzun, H. I., 2001, Mathematical modeling of thin layer solar drying of sultana grapes, Energy, 26 (5), 457-465. |
| [33] | Karathanos, V. T., Belessiotis, V. G., 1997, Sun and artificial air drying kinetics of some agricultural products, Journal of Food Engineering, 31 (1), 35-46. |
| [34] | Kooli, S., Fadhel, A., Farhat, A., Belghith, A., 2007, Drying of red pepper in open sun and greenhouse conditions. Mathematical modeling and experimental validation, Journal of Food Engineering, 79 (3), 1094-1103. |
| [35] | Bennamoun, L., Belhamri, A., 2006, Numerical simulation of drying under variable external conditions: Application to solar drying of seedless grapes, Journal of Food engineering, 76 (2), 179-187. |
| [36] | Dincer, I., 2011, Exergy as a potential tool for sustainable drying systems, Sustainable Cities and Society, 1 (2), 91-96. |
| [37] | Peinado, D., de Vega, M., Garcia-Hernando, N., Marugán-Cruz, C., 2011, Energy and exergy analysis in an asphalt plant’s rotary dryer, Applied Thermal Engineering, 31 (6-7), 1039-1049. |
| [38] | Catton, W., Carrington, G., Sun, Z., 2011, Exergy analysis of an isothermal heat pump dryer, Energy, 36 (8), 4616-4624. |
| [39] | Karamarkovic, R., Karamarkovic, V., 2010, Energy and exergy of biomass dasification at different temperatures, Energy, 35 (2), 537-549. |
| [40] | Nwosu, N.P., 2009, Employing exergy-optimized pin fins in the design of an absorber in a solar air heater, Applied Solar Energy, 45 (4), 248-253. |
| [41] | Liu, Y., Zhao, Y., Feng, X., 2008, Exergy analysis for a freeze-drying process, Applied Thermal Engineering, 28 (7), 675-690. |
| [42] | Liapis, A. I., Bruttini, R., 2008, Exergy analysis of freeze drying of pharmaceuticals in vials on trays, International Journal of Heat and Mass Transfer, 51 (15-16), 3854-3868. |
| [43] | Akpinar, E. K., Midilli, A., Bicer, Y., 2005, Energy and exergy of potato drying process via cyclone type dryer, Energy Conversion & Management, 46 (15-16), 2530-2552. |
| [44] | Holmberg, H., Ahtila, P., 2005, Evaluation of energy efficiency in biofuel drying by means of energy and exergy analyses, Applied Thermal Engineering, 25 (17-18), 3115-3128. |
| [45] | Bennamoun, L., Belhamri, A., 2011, Study of solar thermal energy in the north region of Algeria with simulation and modeling of an indirect convective solar drying system, Nature and Technology, 4, 34-40. |
| [46] | Gbaha, P., Yabouet Andoh, H., Kouassi Saraka, J., Kaménan Koua, B., Touré, S., 2007, Experimental investigation of a solar dryer with natural convective heat flow, Renewable Energy, 32 (11), 1817-1829. |
| [47] | Tiris, C., Ozbalta, N., 1995, Thermal performance of a new solar air heater, International Communications in Heat and Mass Transfer, 22 (3), 411-423. |
| [48] | Boulemtafes-Boukadoum, A., Benzaoui, A., 2011,Energy and exergy analysis od solar drying process of mint, Energy Procedia, 6, 583-591. |
| [49] | Chowdhury, M. M. I., Bala, B. K., Haque, M. A., 2011, Energy and exergy analysis of the solar drying of jackfruit leather, Biosystems Engineering, 110 (2), 222-229. |
| [50] | Youcef-Ali, S., Moummi, N., Desmons, A., Abene, A., Messaoudi, H., Le Ray, M., 2001, Numerical and experimental study odf dryer in forced convection, International Journal of Energy Research, 25(), 537-553. |
| [51] | Bennamoun, L., Belhamri, A., 2008, Mathematical description of heat and mass transfer during deep bed drying: Effect of product shrinkage on bed porosity, Applied Thermal Engineering, 28 (17-18), 2236-2244. |
| [52] | Augustus Leon M., Kumar, S., Bhattacharya, S. C., 2002, A comprehensive procedure for performance evaluation of solar food dryers, Renewable and Sustainable Energy Reviews, 6 (4), 367-393. |
| [53] | Tiris, C., Tiris, M., Dincer, I., 1995, Investigation of the thermal efficiencies of solar dryer, energy Conversion and Management, 36 (3), 205-212. |
| [54] | Bennamoun, L., Belhamri, A., 2008, Study of heat and mass transfer in porous media: Apllication to packed bed drying, Fluid Dynamics and Materials Processing, 4 (4), 221-230. |
| [55] | Kanoglua, M., Dincer, I., Rosen M., A., 2007, Understanding energy ad exergy efficiencies for improved energy management in power plant, Energy Policy, 35 (7), 3967-3978. |
| [56] | Prommas, R., Rattanadecho, P., Cholaseuk, D., 2010, Energy and exergy analyses in drying process of porous media using hot air, Internatinal Communications in heat and Mass Transfer, 37 (4), 372-378. |
| [57] | Midilli, A., Kucuk, H., 2003, Energy and exergy analyses of solar drying process of pistachio, Energy, 28 (6), 539-556. |
| [58] | Celma, A. R., Cuadros, F., 2009, Energy and exergy of OMW solar drying process, Renewable Energy, 34 (3), 660-666. |
| [59] | Sami, S., Etesami, N., Rahimi, A., 2011, Energy and exergy analysis of an indirect solar cabinet dryer based on mathematical modeling results, Energy, 36 (5), 2847-2855. |
| [60] | Dincer, I., Rosen, M. A., 2007, Exergy, Environment and Sustainable Development, analysis of drying processes systems, Elsevier. |
| [61] | Dincer, I., Shahin, A.Z., 2004, A new model for thermodynamic analysis of a drying process, International Journal of Heat and Mass Transfer, 47 (4), 645-652. |
| [62] | Prommas, R., Keangin, P., Rattanadecho, P., 2010, Energy and exergy analyses in convective drying process of multi-layered porous packed bed, International Communications in Heat and Mass Transfer, 37 (8), 1106-1114. |
| [63] | Akbulut, A., Durmuş A., 2010, Energy and exergy analyses of thin drying of mulberry in a forced solar dryer, Energy, 35 (4), 1754-1763. |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML