-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Energy Engineering
p-ISSN: 2163-1891 e-ISSN: 2163-1905
2012; 2(4): 177-183
doi: 10.5923/j.ijee.20120204.10
Frequency Reserve Within Unit Commitment Considering Spinning Reserve Uncertainty
M. Rouholamini , M. Rashidinejad , A. Abdollahi , H. Ghasemnejad
Department of Electrical Engineering, Bahonar University of Kerman, Kerman, Iran
Correspondence to: M. Rashidinejad , Department of Electrical Engineering, Bahonar University of Kerman, Kerman, Iran.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Various technical limitations of generating units and ancillary services requirements have more complicated the power generation control and operation. This paper introduces a novel methodology for day-ahead unit commitment, which is a crucial challenge in restructured power systems, considering primary frequency control reserve. In addition, also spinning reserve uncertainty as a practical constraint has been taken into account. In this paper, we formulate and solve simultaneous scheduling of energy and primary reserve as a mixed integer non linear programming problem that simultaneously accounts aforementioned constraints. In proposed formulation, system frequency is allowed to fall from nominal value to a critical specified limit.Finally, the proposed approach is implemented to the scheduling of a 17-unit isolated power system over 24-hours. Case studies and numerical results present significant outcomes and verify the robustness of the proposed method, while it creates a schedule consistent with the primary frequency control and spinning reserve uncertainty.
Keywords: Frequency Deviation, GAMS, Load Ramp Rate, MINLP, Primary Reserve, Simultaneous Scheduling, Spinning Reserve Probability
Article Outline
1. Introduction
- A power system is always exposed to sudden variation, unwanted changes in system demand or losing generating units that cause a frequency deviation in system frequency. In particularly, a change in system load or loss a generating unit will results in a steady-state frequency deviation, depending on the governor droop characteristic. So the frequency regulating will be arisen. Frequency regulating is one of most important challenges for Independent System Operator (ISO, hereinafter) or market operator inderegulated electricity industry. In restructured power systems, frequency regulating can be considered as an ancillary service (AS, hereinafter) that will be supplied employing the eligible resources provided by market participants. Usually, preparation reserve capability is called as "frequency control reserve", which is classified as primary, secondary and tertiary reserve. This categorization depends on the response time of frequency control reserves and how they are deployed[1],[2]. Primary frequency reserve is madeavailable by a set of individual participating generators. Actually the primary reserve is obtained mainly from the response of governor droop characteristic to system frequency deviation from nominal. This is the fastest of the three aforementionedreserve control strategies with a response time of the order of seconds[3]. The secondary reserve, called as Automatic Generation Control (AGC, hereinafter) and morespecifically Load Frequency Control (LFC) is with a response time of the order of minutes. AGC is applied to regulate the area control-error. Area control -error is defined as tie-lines flow violation versus frequency deviation in a multi-area power network[4]. Secondary reserve is with a response time reported as one minute. The tertiary reserve, with a response time of the order of minutes, can be used for congestion management, improvement of lost reserves andcompensation of the incomplete tasks that has not completely been done by AGC. In this paper, we just emphasized the primary reserve without considering the secondary and tertiary reserves.Previous researches indicate that scheduling of energy and AS are developed using simultaneously or sequentially methods in different countries[3],[4]. Form market point of view, energy and AS are transacted simultaneously while technically ancillary services will be produced afterpreparation of energy in sequential scheduling. Using sequential scheduling method, it is possible that "price reversal" be occurred, where this event has been experienced in California and Newengland[5]. Simultaneous scheduling is more complex in comparison with sequential scheduling but it may converge to a global optimal solution. In addition, it is possible, the final solution of sequential method may be not applicable[5].Reference[6] is one of most important researches about scheduling of energy and primary reserves which has employed an iterative economic dispatch and in it; the generation output and reserve of each unit are modified successively. In[7], operational and stability constraints have been considered in scheduling problem using decision tree solution method. However, in both of the above mentioned approaches, generation is scheduled a priori and then the reserve is scheduled. Since the type of simultaneous scheduling of energy and frequency reserve is MINLP, in[3], this problem has been solved through converting MINLP into a Mixed Integer Linear Programming (MILP) problem, to be solved by means of commercially available mixed integer software, such as GAMS. This software has been commonly applied to solve many crucial combinatorial optimization problems but the linearization of the quadratic objective function may cause a deviation in final solution. One previous important contribution is the work reported in[8] by Galiana and colleagues. They indicated that simultaneous scheduling of energy and frequency control reserves increases social welfare. From the aforementioned researches it seems clear that the scheduling of rapid primary frequency regulation reserve within the unit commitment problem has received relatively little attention formulating as simultaneous method. This paper focuses on simultaneous scheduling of energy and primary reserve and supposes the system is isolated. In the other words the AGC not installed on the system. Here, the contingency has been assumed as the case of lose of one generating unit. This criterion is suggested by North American Electric Reliability Council. In continue, the simultaneous scheduling of energy and primary frequency control reserve is presented and the optimization problem will be formulated as a MINLP problem to be solved using GAMS software. Finally, the effectiveness of the proposed approach is examined on a 17-unit case study in details. A multiperiod unit commitment problem that simultaneously schedules generated power and primary reserves is tested to validate the proposed formulation. This formulation is subject to accounting for spinning reserve uncertainty, start up cost, a security criterion defined by one of prespecified generation outage contingencies and by the explicit requirement that the system frequency must not fall below a specified lower bound under any of the contingencies.
2. Primary Frequency Control Reserve
- Frequency deviation that stimulates the governor response is mainly caused due to unbalances between generation and demand in power system. Inherent demand randomness is the major reason of these mismatches, which, being generally small and relatively slows, can be corrected by secondary regulation or AGC. Under such conditions, primary regulation is also active, helping keep frequency within bounds, but not in a very conspicuous fashion. It is obviously, following a large imbalance between demand and generation, for example lose of a generating unit, primary frequency regulation is very essential in limiting frequency deviation and preventing system outage by maintaining a balance between generation and demand. Following lose of a generating unit, system frequency drops from its reference level. Calling this frequency deviation by ∆f, remaining generating units perforce responds through their speed governors by automatically incrementing their outputs according to –Ri×∆f. Ri is the slope of the droop curve and it is generally between 4 and 6%. Incrementing of healthly generating units output will be continued until the system frequency reaches steady-state at a value that causes the sum of the on-line generators output to be equal to the system load. Governor response stabilizes the system frequency within 5 to 10 s. Thus, when referring to system frequency deviation, in this paper, we mean the steady-state value ∆f reached after the post-contingency transient dies down. We know that with conventional type of governors, when the systems load increases, the system frequency decreases and vice versa. At the same aforementioned important, following losing a generating unit under -frequency relay operation may be occurred. It is clearly, decrease in system frequency versus losing a generating unit must be restricted to a critical specified limit in the steady state, typically around 1% below the nominal frequency called as ∆fcr hereinafter. Once the system is in steady state, within minutes, tertiary reserves are deployed to bring the system frequency back to nominal, since secondary reserves and AGC may be insufficient to compensate for the lose of a large generating unit.The significant time gap between a major contingency and the start of secondary and tertiary corrective actions (in the order of minutes) and preventing under-frequency relay operation means that primary frequency regulation is essentially responsible for initially balancing power and stabilizing the system frequency[3]. It should be noted that loads response to frequency deviation inherently, however it is neglected in following problem formulation.
3. Problem Formulation
- In this section, problem formulation of simultaneousscheduling of energy and primary reserve considering spinning reserve uncertainty are presented for an isolated power system. The power market in this paper is assumed as pay as bid and the contingency has been modeled as N-1 in formulation.In continue, formulation of primary reserve and spinning reserve uncertainty are illustrated following generalformulation of unit commitment problem. Finally objective function is expressed to minimize overall cost of both generation and primary reserve provision over the scheduling horizon. A Unit commitment constraintsThe UC problem is subjected to the followingconstraints[9-13]:• Power balance constraintHere the system loss has been neglected. In condition of considering power losses, total generating output must be equal to demand plus losses during each hour.• Unit output limits
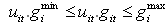 | (2) |
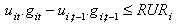 | (3) |
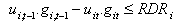 | (4) |
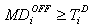 | (5) |
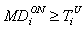 | (6) |
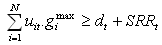 | (7) |
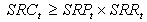 | (8) |
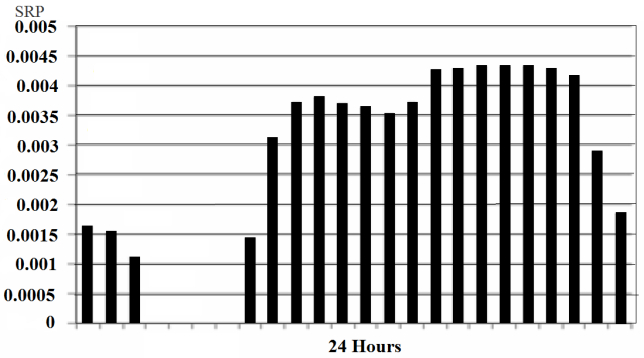 | Figure 1. Forecasted probability that spinning reserve is called and generated |
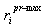 , or by unit spinning capacity limit,
, or by unit spinning capacity limit, 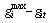 , whichever is smaller[3],[5],[6]. Unit frequency-regulation ramp limit is the maximum reserve that a unit can produce within 10 seconds following a contingency[6].
, whichever is smaller[3],[5],[6]. Unit frequency-regulation ramp limit is the maximum reserve that a unit can produce within 10 seconds following a contingency[6]. 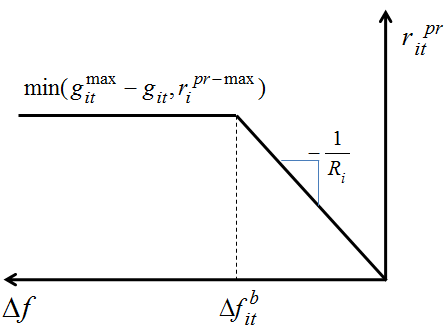 | Figure 2. Primary reserve characteristic |
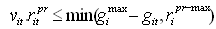 | (9) |
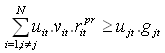 | (10) |
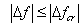 | (11) |
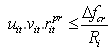 | (12) |
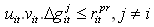 | (13) |
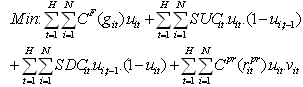 | (14) |
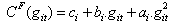 | (15) |
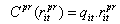 | (16) |
4. Optimization Method
- The type of simultaneous scheduling of energy and primary reserve is a Mixed Integer Non Linear Programming (MINLP) problem[16]. Where the binary variables are the representation of on/off status and continual variables represent the values of generation and reserves. In solving this problem an important challenges arise: the fact that value of primary reserve of unit i must lie on the piece-wise curve imposed by Fig. 1, which is described by four decision criterions including the spinning reserve capacity of unit i, ramp up limit of unit i, the allowed frequency deviation and the corresponding frequency deviation is another. GAMS (Generalized Algebra Modeling System) is one of most popular commercial software in algebraic modeling of optimization problems including integer and continual variables. It is a computer environment that can easily be used to model and solve optimization problems. GAMS is specially design for linear, nonlinear and mixed integer optimization and has been commonly applied to solve power system optimization problems[19],[20]. Even though it is required some effort to become familiar with GAMS, in following we will see that this is a very comprehensive and powerful tool to solve unit commitment with primary frequency regulation constraints.
5. Case Study and Simulation Results
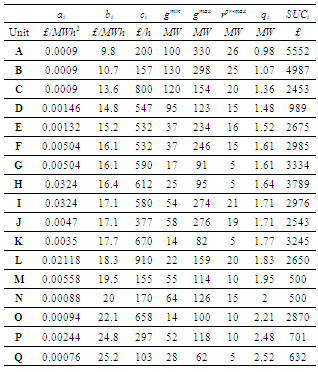
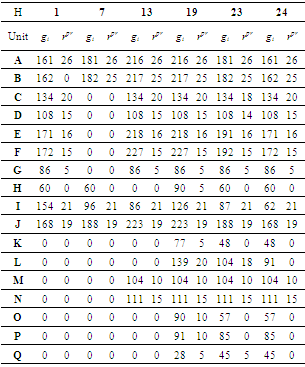
- In this paper, it is assumed that each unit can lie in three modes which are: 1) unit is shut down, 2) unit is turn on and provides energy but does not participate in frequency control, 3) unit is turn on and participates in both generation and primary frequency regulation as shown in Table 1. Notice, a shut down unit cannot participate in primary frequency control.
|
|
|
6. Conclusions
- In this paper a simultaneous multi period unit commitment problem subject to primary regulation reserve constraints is formulated. In the other hand, the spinning reserve probability as a practical constraint has been taken into account. This problem has not received as much attention in the previous works. In addition, for committed generating units three alternatives are defined including participating in both generation and primary frequency control, just participating in generation and finally disaffiliation in generation and supplying primary reserve. It is also not considered in the previous researches. In this paper, only credible contingencies, negative frequency deviation following each contingency have been considered.Finally, the proposed optimization method has been implemented on a test system including 17 generating units, a well-known test system. Results indicate that the final solution is applicable.Although the methodology presented has been examined on a small isolated power utility but it is practical even for large systems.
ACKNOWLEDGEMENTS
- We are thankful to South Kerman Electrical Distribution Company for their support and also many thanks go in particular to Dr.Mashhadi, Dr.Javidi and Dr.Ghazizadeh for their valuable work reported in[5].
Numencalture
- A. Continuous Variables
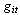 Scheduled generation of unit i in the pre contingency state during time period t
Scheduled generation of unit i in the pre contingency state during time period t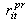 Scheduled primary reserve of unit i during time period t
Scheduled primary reserve of unit i during time period t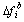 Break Frequency deviation of unit i
Break Frequency deviation of unit i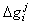 Generation deviation in output of unit i after contingency due to outage of unit jB. 0/1 Binary Variables
Generation deviation in output of unit i after contingency due to outage of unit jB. 0/1 Binary Variables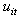 A variable defining the operation status of generator i during time period t (equals 1 if the unit is on and zero if it is off)
A variable defining the operation status of generator i during time period t (equals 1 if the unit is on and zero if it is off)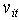 A variable defining the operation status of governor of generating unit i (equals 1 if the governor be in active mode and zero if not)
A variable defining the operation status of governor of generating unit i (equals 1 if the governor be in active mode and zero if not)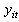 Equals 1 if unit i turns on during time period and equals zero if it does not.
Equals 1 if unit i turns on during time period and equals zero if it does not.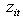 Equals 1 if unit i turns off during time period t and equals zero if it does notC. Parameters
Equals 1 if unit i turns off during time period t and equals zero if it does notC. Parameters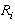 Governor droop of unit i
Governor droop of unit i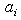 Unit i quadratic generation cost parameter
Unit i quadratic generation cost parameter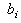 Unit i linear generation cost parameter
Unit i linear generation cost parameter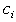 Unit i fixed generation costCF (git) Fuel cost
Unit i fixed generation costCF (git) Fuel cost 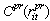 Cost of supplying primary reserve
Cost of supplying primary reserve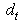 System demand during time period t
System demand during time period t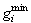 Minimum possible generation output of unit i
Minimum possible generation output of unit i 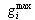 Maximum possible generation output of unit i H Unit commitment horizonMDiOFF Duration during which the ith unit is continuously onMDiON Duration during which the ith unit is continuously offN Number of units
Maximum possible generation output of unit i H Unit commitment horizonMDiOFF Duration during which the ith unit is continuously onMDiON Duration during which the ith unit is continuously offN Number of units 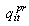 Primary reserve price during time period t for unit i
Primary reserve price during time period t for unit i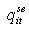 Secondary reserve price during time period t for unit i
Secondary reserve price during time period t for unit i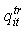 Tertiary reserve price during time period t for unit iRURi Ramp up rate limit of unit iRDRi Ramp down rate limit of unit i
Tertiary reserve price during time period t for unit iRURi Ramp up rate limit of unit iRDRi Ramp down rate limit of unit i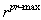 Unit i ramp-up limit under primary regulationSDCit Shut down cost of unit i at hour tSRC Spinning reserve capacitySRR Spinning reserve requirementSUCit Start up cost of unit i at hour tTiD Minimum down time limit of unit iTiON Minimum up time limit of unit i
Unit i ramp-up limit under primary regulationSDCit Shut down cost of unit i at hour tSRC Spinning reserve capacitySRR Spinning reserve requirementSUCit Start up cost of unit i at hour tTiD Minimum down time limit of unit iTiON Minimum up time limit of unit i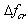 Critical frequency deviation allowed
Critical frequency deviation allowed
References
| [1] | A.J.Wood, B.F.Wollenberg, “Power generation operation and Control “ (2nd Ed. New York: Wiley, 1996). |
| [2] | R. J. Koessler, J. W. Feltes, J. R. Willis, “A methodology for management of spinning reserves requirements ”, Proc. IEEE Power Eng. Soc. Winter Meeting, vol. 1, Feb. 1999, pp. 584–589. |
| [3] | Jose’ F.Restrepo, Francisco D.Galiana, “Unit commitment with primary frequency regulation constraints” ,IEEE Trans.Power Syst. ,vol.20, no.4,pp.1836-1843, Nov 2005. |
| [4] | N. Jalleli, D. N. Ewart, L. H. Fink, A. G. Hoffmann, “Understanding automatic generation control”, IEEE Trans. Power Syst., vol. 7,no. 3, pp. 1106–1112, Aug. 1992. |
| [5] | M.R.Mashhadi, M.H.Javidi, M.S.Ghazi zadeh, “The impacts of capabilities and constraints of generating units on simultaneous scheduling of energy and primary reserve”, Electrical Engineering, pp. 1-10. doi:10.1007/s00202-010, 2011 |
| [6] | J.W.O’Sullivan, M.J.O. Malley, “A new methodology for the provision of reserve in an isolated power system”, IEEE Trans.Power Syst., vol.14, no.2, pp.519-523, May 1999. |
| [7] | K.A.Papadogiannis, N.D.Hatziagyriou, “Optimal allocation of primary reserve services in energy markets”, IEEE Trans.Power Syst. vol.19, no.1, pp.519-523, Feb.2004. |
| [8] | Fransisco D.Galiana, Franccois Bouffard, Jose M.Arroyo, Jose’ F.Restrepo, “Scheduling and pricing of coupled energy and primary, secondary, and tertiary reserves”, Proceedings of the IEEE, pp.1970-1984, vol.93, no.11, 2005. |
| [9] | M.Pourakbar-Kasmaie, M.RashidiNejad, “A novel unit commitment technique considering prohibited zones”, Journal of applied science, vol.9.n.16. pp 2962-2968, 2009. |
| [10] | A.Abdollahi, M.Ehsan, M.Rashidi-Nejad, M.Pourakbar-Kasmaie, “cost-based unit commitment considering prohibited zones and reserve uncertainty”, Journal of IREE, vol.4, N.3, pg:425-433,May-June 2009. |
| [11] | S.J.Huang, C.L.Huang. “Application of Genetic-Based Neural Network to Thermal Unit Commitment”, IEEE Trans Power Syst.12 (1997) 654-660. |
| [12] | C.Wang, SM.Shahidehpour. “Affect of Ramp-Rate Limits on Unit Commitment and Economic Dispatch”. IEEE Trans on Power Syst.8 (3) (1993) 1341-1350. |
| [13] | Vo Ngoc Dieu, Weerakorn Ongsakul. “Ramp Rate Constrained Unit Commitment by Improved Priority List and Augment Lagrange Hopfield Network, EPSR.78(3) (2008) 291-301. |
| [14] | Bruce A. Grey, Ghadir Radman, Arun Sekar, “Determination of Spinning Reserve Deployment using an Extended Economic Dispatch to Include Line Flow Limits and Primary Frequency Regulation”. 39th Southeastern Symposium on System Theory, Mercer University, March 4-6, 2007. |
| [15] | Fushan Wen, A.K.David, “Coordination of bidding strategies in day-ahead energy and spinning reserve markets”, Jour nal of Electrical power and energy systems, vol.24, pg:251-261, April.2002. |
| [16] | H.Y. Yamin, Q.El-Dwairi, S.M.Shahidehpour,“ A new approach for GenCos profit based unit commitment in day-ahead competitive electricity markets considering reserve uncertainty”. EPES.29(2007) 609-616. |
| [17] | M.Rouholamini, M.Rashidi-nejad, S.Esmaeili, “A new methodology to solve joint energy and primary reserve scheduling” 5th power control and optimization conference. UAE, Doubai., in press. |
| [18] | Jose Restrepo, “Unit Commitment with Primary Frequency Regulation Constraint in Electric Power System”, Ph.D. dissertation, department of electrical and computer of McGill University, February 25, 2005. |
| [19] | D. Chattopadhyay, “Application of general algebraic modeling system to power system optimization”, IEEE Transactions on Power Systems, vol. 14, no. 1, February 1999, pp. 15 – 22. |
| [20] | Bhujanga B Chakrabarti, Doug Goo win, Nirmal-Kumar C Nair, “Power system congestion - in search of an index from LP basis matrices”, Power Engineering Society General Meeting,. IEEE, june 2007. |
| [21] | Reliability test system task force, The IEEE reliability test system– 1996, IEEE Trans. Power Syst., vol. 14, no. 3, pp. 1010 1020, Aug. 1999. |
| [22] | GAMS solver manuals, http://www.gams .com/solvers. |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML