-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Energy Engineering
p-ISSN: 2163-1891 e-ISSN: 2163-1905
2012; 2(4): 165-170
doi: 10.5923/j.ijee.20120204.08
Multi Objective For Optimal Reactive Power Flow Using Modified PSO Considering TCSC
N. Mancer , B. Mahdad , K. Srairi , M. Hamed
Department of Electrical Engineering, University of Biskra, Biskra (07000), Algeria
Correspondence to: B. Mahdad , Department of Electrical Engineering, University of Biskra, Biskra (07000), Algeria.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Multi objective optimal reactive power flow considering FACTS technology is becoming one of the most important issue in power system planning and control. This paper presents a new variant of particle swarm algorithm with time varying acceleration coefficients (TVAC) to solve multi objective optimal reactive power flow (MOORPF) (power loss minimization and voltage deviation). The proposed algorithm is used to adjust dynamically the parameters setting of Thyristor controlled series capacitor (TCSC) in coordination with voltages of generating units. This study is implemented on the standard IEEE 30-Bus system and the results are compared with other evolutionary programs such as simple genetic algorithm (SGA) and the simple particle swarm algorithm (SPSO). Simulation results confirm robustness of this new variant based PSO in term of solution quality and convergence time.
Keywords: Optimal Reactive Power Flow (ORPF), Multi Objective, Loss Minimization, Voltage Deviation, TCSC, PSO, Time Varying Acceleration Coefficient (TVAC)
Article Outline
1. Introduction
- Optimal reactive power flow (ORPF) plays an important role in optimal operation problems of power system[1], which referred to assign certain variable such generator voltage, tap ratios of transformers, shunt capacitor or reactor to minimize the real power loss, voltage deviation or any other objective function. This optimization should satisfy a given set of constraints which come from physical and operational limitations.Many classic optimization techniques such linear and non-linear programming[2], quadratic programming[3], and interior point method[4] have been applied for solving ORPF problem. These methods are incapable in handling non-linear, discontinuous function and constraints, and problems having multiple local minimum points.Recently, stochastic search methods have been used widely for the global optimization problem. These method have been successfully used to solve the ORPF problem. In[5] Lee used simple genetic algorithm (SGA) to solve reactive power operational problem, Mahdad in[6] proposed the application of GA for Optimal Power Flow with Consideration of FACTS devices. Particle swarm optimization (PSO) was applied by Yoshida in[7] for reactive power and voltage control. Krishna in[8] proposed a solution to the economic power dispatch problem with PSO with time varying acceleration coefficients for non-convex objective functions. The classical particle swarm optimization (PSO) first introduced by Kennedy and Eberhart 1995[9], this method applied with success to solve the reactive power planning, PSO developed through simulation of a simplified social system, and has been found to be robust and flexible in solving optimization problem. because this technique can generate a high-quality solution within shorter calculation time and stable convergence characteristic than other stochastic methods.The concept of Flexible AC Transmission Systems (FACTS) was first defined by N.G. Hingorani, in 1988[10]. A Flexible Alternating Current Transmission System (FACTS) is defined by the IEEE as “a power electronic based system and other static equipment that provide control of one or more AC transmission system parameters to enhance controllability and increase power transfer capability”[11]. FACTS devices can be utilized to increase the transmission capacity, improve the stability and dynamic behaviours or ensure better power quality in modern power systems in comparison to conventional devices like switched compensation. Hence, there is an interest in better utilization of available capacities bay installing flexible AC transmission systems (FACTS) devices[10-15] such as Thyristor controlled series compensators (TCSC).The TCSC is an important member of the FACTS family. It allows rapid and continuous changes of the transmission line impedance[12-14]. Active power flow across the compensated transmission line can be maintained at a specified level under a wide range of operating conditions. This paper investigates the application of PSO algorithm and the advantage of the TCSC for reactive power dispatch to minimize real power loss in transmission network and reduce the voltage deviation.In this work a new variant of PSO based on time varying acceleration coefficient (TVAC) is proposed to solve the multi objective optimal reactive power planning considering TCSC Controllers. The proposed algorithm is validated on the standard IEEE 30-Bus test system and compared to SGA and SPSO. Simulation results confirm efficiency of this variant in term of solution quality and convergence time.
2. Multi-Objective ORPF Formulation
- The multi objective ORPF is to optimize the settings of control variables in terms of one or more objective functions while satisfying several equality and inequality constraints. In multi objective ORPF we have to optimize two or more objective functions simultaneously. The problem can be formulated as:Minimize:
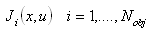 | (1) |
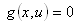 | (2) |
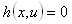 | (3) |
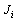 is the ith objective function, and
is the ith objective function, and 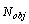 is the number of objectives. G is the equality constraints, h is the system operation constraints. The main objective of this work is to optimize two competing objective functions, power loss and voltage deviation, while satisfying several equality and inequality constraints. The function can be written in the following[16]:
is the number of objectives. G is the equality constraints, h is the system operation constraints. The main objective of this work is to optimize two competing objective functions, power loss and voltage deviation, while satisfying several equality and inequality constraints. The function can be written in the following[16]: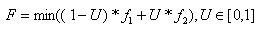 | (4) |
 the two objective functions to be optimized simultaneously.
the two objective functions to be optimized simultaneously.2.1. Objectives Functions
- 2.1.1. Real Power loss (RPL)The first objective of the reactive power optimization is to minimize the real power loss in the transmission network, which is defined as follows:
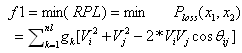 | (5) |
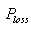 is the active power loss,
is the active power loss, 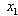 is the control variable vector
is the control variable vector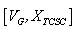 represented the generator voltage (continuous) and the series capacitor/inductor respectively, x2 is the dependent variable vector
represented the generator voltage (continuous) and the series capacitor/inductor respectively, x2 is the dependent variable vector 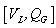 ,
, 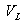 is the load-bus voltage,
is the load-bus voltage, 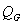 is the generator reactive power,
is the generator reactive power, 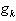 is the conductance of branch between bus i and j,
is the conductance of branch between bus i and j, 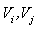 is the voltage at bus i-j.
is the voltage at bus i-j.2.1.2. Voltage Deviation (VD)
- This objective function is to minimize the deviations in voltage magnitudes at load bus that can be expressed through the following equation:
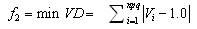 | (6) |
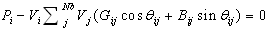 | (7) |
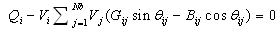 | (8) |
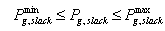 | (9) |
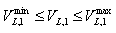 | (10) |
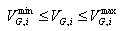 | (11) |
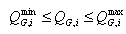 | (12) |
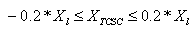 | (13) |
3. Modeling of TCSC
- The TCSC is a series compensation component which consists of a series capacitor bank shunted by Thyristor controlled reactor as presented in Fig.1.
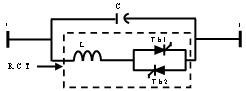 | Figure 1. Basic TCSC configuration |
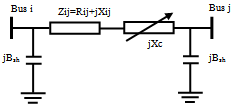 | Figure 2. Single line diagram of TCSC model |
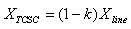 | (14) |
4. PSO Strategy Based Time Varying Acceleration Coefficients
- Since the introduction of PSO method, a number of different PSO strategies are being applied by researchers for solving the ORPF, and other complex problem.PSO is a based modern heuristic search method motivated from the simulation of the behaviour of social systems such as fish schooling and birds flocking[8-9]. The motivation behind this concept is to well balance the exploration and exploitation capability for attaining better convergence to the optimal solution. The PSO beginning, a population of particles is initialized with random positions marked by vectors xi and random velocities vi, population of such particles is called a “swarm”. The particles update their positions using their own experience and the experience of their neighbors. The update mode is termed as the velocity of particles[17].The modified velocity and position of each particle can be calculated using the current velocity and the distance from
 to
to 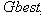 as shown in the following formulas general:
as shown in the following formulas general: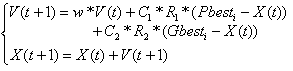 | (15) |
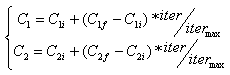 | (16) |
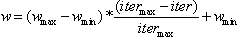 | (17) |
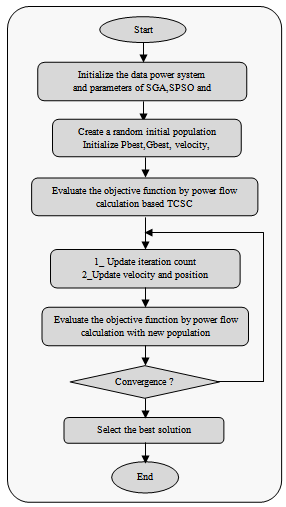 | Figure 3. Flow Chart of the proposed algorithm based GA, SPSO and PSO-TVAC considering TCSC |
5. Simulation and Numerical Results
- The proposed algorithm is implemented and tested on a standard IEEE 30-Bus test system[18]; it consists of 6 generators located at buses 1, 2, 3, 5, 8, 11, and 13, 41 branches (lines) and four transformers in line 6-9, 6-10, 4-12, and 28-27. In this study in all cases one TCSC installed at the branch 27-28. The algorithms were implemented using the Matlab programming language; detailed analyses of the results are presented and discussed in this section.A. Testing StrategiesCase 1: Single objective function: Ploss minimization with and without TCSC Controller.The main goal of this first case is to verify the feasibility and performance of the new proposed PSO variant based time varying acceleration to solve the ORPF problem. Table 1 shows the parameters of SGA, SPSO and PSO-TVAC. Figs 4-5-6 show the convergence characteristics of active power loss for SGA, SPSO and PSO-TVAC.
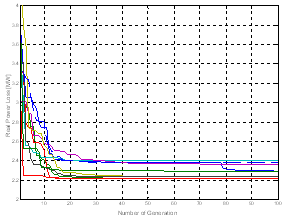 | Figure 4. Convergence characteristic of real power loss based SGA |
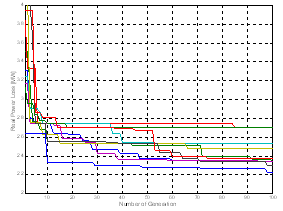 | Figure 5. Convergence characteristic of real power loss based SPSO |
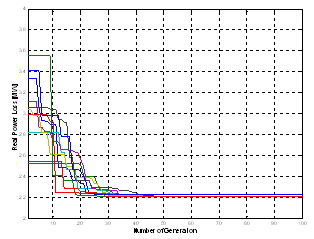 | Figure. 6. Convergence characteristic of real power loss based PSO-TVAC |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
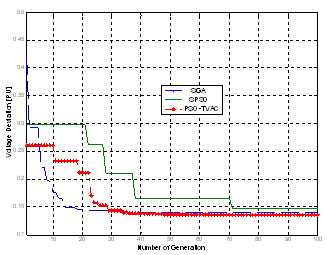 | Figure 7. Convergence characteristics for voltage deviation using PSO-TVAC, GA and PSO |
| |||||||||||||||||||||||||||||||||||||||||||||
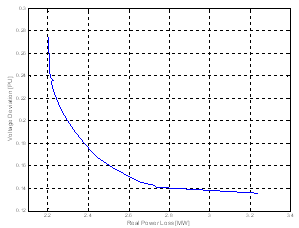 | Figure 8. Pareto optimal solution results based PSO-TVAC |
6. Conclusions
- This paper presents the application of modified variant of PSO using time varying acceleration to adjust dynamically the reactance of TCSC controller in coordination with voltage control of generators to improve the multi-objective ORPF solution. Comparing the proposed algorithm with two other techniques (SGA and PSO) shows the advantage of this algorithm in decreasing transmission loss and voltage deviation. Also the results obtained demonstrate the performances of the proposed approach based PSO-TVAC in term of solution quality and convergence characteristic.
References
| [1] | Zhang X, Chen W, Dai C, Cai W. ‘‘Dynamic multi-group self-adaptive differential evolution algorithm for reactive power optimization’’, Elect Power and energy syst, 2010, 32,pp.351–357. |
| [2] | N. Deeb, S.M. Shahidepour, Linear reactive power optimization in a large power network using the decomposition approach, IEEE Trans. Power Syst. 5 (2) (1990) 428–435. |
| [3] | J.A. Momoh, S.X. Guo, E.C. Ogbuobiri, R. Adapa, The quadratic interior point method solving power system optimization problems, IEEE Trans.Power Syst. 9 (3) (1994) 1327–1336. |
| [4] | S. Granville, Optimal reactive dispatch through interior point methods, IEEE Trans. Power Syst. 9 (1) (1994) 136–146. |
| [5] | Lee KY,Bai X,Park YM. ‘’optimization methode for reactive power planning by using a modified simple genetic algorithm’’. IEEE trans power syst, vol 10 no, 4; 1995 p1843-50. |
| [6] | B. Mahdad, Optimal Power Flow with Consideration of FACTS devices Using Genetic Algorithm: Application to the Algerian Network, Doctorat Thesis, Biskra University Algeria, 2010. |
| [7] | Yoshida H, Fukuyama Y, Kawata K, Takayama S, Nakanishi Y. ‘‘A particle swarm optimization for reactive power and voltage control considering voltage security assessment,’’ IEEE Trans Power Syst 2001,15(4),pp1232–1239. |
| [8] | TC Krishna, P Manjaree, S Laxmi.’’ Particle swarm optimization with time varying acceleration coefficients for non-convex economic power dispatch.’’ , Elect Power and energy syst, 2009, 31,pp.249-257. |
| [9] | J Kennedy, R Eberhart., ‘‘Particle swarm optimization’’ In: Proceedings of the IEEE conference on neural networks (ICNN’95), vol. IV. Perth, Australia; 1995. pp.1942–1948. |
| [10] | N.G. Hingorani, L. Gyugyi, ‘’Understanding FACTS – Concepts and Technology of Flexible AC Transmission Systems’’, IEEE Press, New York, 2000. |
| [11] | K. R. Padiyar . ‘’FACTS controllers in power transmission and distribution ‘’, New age international publishers, 2007. |
| [12] | R.Benabid, M.Boudour,M.A Abido.’’Optimal location and setting of SVC and TCSC devices using non-dominated sorting particle swaem optimization’’. Elect Power and energy syst, 2009, 79,pp.1668-1677. |
| [13] | K. shanmukha Sundar, H.M. Ravikumar,’’selection of TCSC location for securd optimal power flow under normal and network contingencies’’ Elect Power and Energ Syst , 2012, 34,pp 29-37. |
| [14] | P. L. So, Y. C. Chu, T. Yu, “Coordinated control of TCSC and SVC for system damping enhancement”, International Journal of Control, Automation, and Systems, June 2005Vol. 3, No. 2, pp 322-33. |
| [15] | B. Mahdad “Contribution to the improvement of power quality using multi hybrid model based Wind-Shunt FACTS,” 10th EEEIC International Conference on Environment and Electrical Engineering, Italy, 2011. |
| [16] | M.A. Abido. ‘‘A novel multiobjective evolutionary algorithm for environmental/economic power dispatch’’ Elect Power Syst Res, 2003, 65,pp 71-81. |
| [17] | RC. Eberhart, Y. Shi. ‘’Comparing inertia weights and constriction factors in particle swarm optimization’’. Proc Congr Evol Comput 2000;1,pp 84-88 |
| [18] | www.pserc.cornell.edu/matpower/, Package of MATLAB, MATPOWER. |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML