-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Energy Engineering
p-ISSN: 2163-1891 e-ISSN: 2163-1905
2012; 2(2): 1-7
doi: 10.5923/j.ijee.20120202.01
Multi Objective Optimal Reactive Power Flow Based STATCOM Using Three Variant of PSO
N. Mancer , B. Mahdad , K. Srairi
Department of Electrical Engineering, University of Biskra, Biskra (07000), Algeria
Correspondence to: B. Mahdad , Department of Electrical Engineering, University of Biskra, Biskra (07000), Algeria.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
This paper proposes, an efficient variant of particle swarm optimization (PSO) to solve the multi-objective optimal reactive power flow (ORPF) based flexible AC transmission system (FACTS) using multi STATCOM Controllers by adjusting dynamically their parameters setting. Two objectives function are considered (power loss and voltage deviation) to validate the robustness of the proposed approach. The performance of the proposed variant based PSO approach has been tested on the standard test system IEEE 30-bus; simulation results compared to the standard PSO confirm the effectiveness of the proposed variant to solving the multi-objective reactive power considering multi STATCOM Controllers.
Keywords: Reactive Power Optimization , Particle Swarm Optimization (PSO), FACTS, Multi Objective, STATCOM
Article Outline
1. Introduction
- The optimal reactive power flow (ORPF) is one of important optimization in power system. The reactive power optimization problem is multi-variable, non differentiable and non-linear[1], furthermore it involves controlling of continuous and discrete variable. The objective of ORPF problem is optimization a certain variables to minimize an objective function for example the active power loss, and voltage deviation by adjustment of the voltage level of the generation, switched capacitor shunt and the tab of the transformer, while satisfying the physical and operational constraint equality and constraint inequality. Many techniques ranging from conventional mathematical methods have been proposed to deal with reactive power dispatch, such as traditional method including linear programming[2] non- linear programming[3]; quadratic programming[4] and interior point methods[5], this method can not ensure the acquirement of the whole optimization. To overcome the drawbacks of the conventional methods, a variety of global optimization[6] techniques have been successfully used to solve the ORPF problem, these optimization techniques including, genetic algorithm (GA)[7], particle swarm optimization (PSO)[8], Tabu search (TS)[9], differential evolution (DE)[10,11], and they are now considered as a promising alternative to solve this kind of problem. The classical particle swarm optimization (PSO) first in- troduced by Kennedy and Eberhart 1995[12], this method applied with success to solve the reactive power planning, PSO developed through simulation of a simplified social system, and has been found to be robust and flexible in solving optimization problem, because this technique can generate a high-quality solution within shorter calculation time and stable convergence characteristic than other stochastic methods. Recently the new technology known as FACTS introduction to system electricity to improve the performance of the large practical electrical network. The concept of Flexible AC Transmission Systems (FACTS) was first defined by N.G. Hingorani, in 1988[13]. A Flexible Alternating Current Transmission System (FACTS) is defined by the IEEE as “a power electronic based system and other static equipment that provide control of one or more AC transmission system parameters to enhance controllability and increase power transfer capability”[14]. FACTS-devices can be utilized to increase the transmission capacity, improve the stability and dynamic behavior or ensure better power quality in modern power systems in comparison to conventional devices like switched compensation. The FACTS controllers based on voltage source converter (VSC) have several and advantages over the variable impedance type, for example, a STATCOM [15,16] is much more compact than a SVC[17] for similar rating and is technically superior. It can supply required reactive current even at low values of the bus voltage. In this work a three variant of PSO are proposed to solve the multi objective optimal reactive power planning based multi STATCOM Controllers, the basic idea behind these variants related in a flexible control of swarm position (velocity variation) coordinated with dynamic control of shunt FACTS devices based multi STATCOM Controllers.
2. Multi Objective ORPF Formulation
- The multi objective ORPF is to optimize the settings of control variables in terms of one or more objective functions while satisfying several equality and inequality constraints. In multi objective ORPF we have to optimize two or more objective functions simultaneously. The problem can be formulated as:Minimize
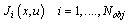 Subject to :
Subject to : 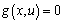 (1)
(1)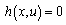 (2)Where Ji is the ith objective function, and Nobj is the number of objectives. G is the equality constraints, h is the system operation constraints. The main objective of this work is to optimize two competing objective functions, power loss and voltage deviation, while satisfying several equality and inequality constraints. The function can be written in the following[18,15,16]:
(2)Where Ji is the ith objective function, and Nobj is the number of objectives. G is the equality constraints, h is the system operation constraints. The main objective of this work is to optimize two competing objective functions, power loss and voltage deviation, while satisfying several equality and inequality constraints. The function can be written in the following[18,15,16]: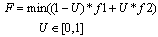 | (3) |
2.1. Objectives Functions
- a. Power loss The first objective of the ORPF problem is to minimize the active power loss in the transmission network, which is defined as follows:
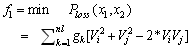 | (4) |
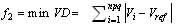 | (5) |
2.2. Constraints
- The equality constraints represent the power flow equations
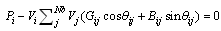 | (6) |
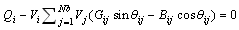 | (7) |
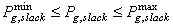 | (8) |
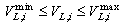 | (9) |
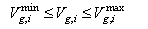 | (10) |
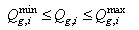 | (11) |
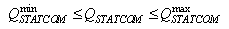 | (12) |
3. PSO Strategy
- Since the introduction of PSO method, a number of different PSO strategies are being applied by researchers for solving the ORPF, and other complex problem.PSO is a based modern heuristic search method motivated from the simulation of the behaviour of social systems such as fish schooling and birds flocking[12]. The motivation behind this concept is to well balance the exploration and exploitation capability for attaining better convergence to the optimal solution. The PSO beginning, a population of particles is initialized with random positions marked by vectors xi and random velocities vi, population of such particles is called a “swarm”. The particles update their positions using their own experience and the experience of their neighbours. The update mode is termed as the velocity of particles[19].The modified velocity and position of each particle can be calculated using the current velocity and the distance from Pi to Pg as shown in the following formulas general:
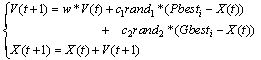 | (13) |
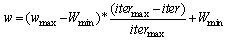 | (14) |
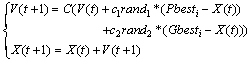 | (15) |
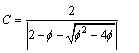 | (16) |
|
4. Modeling of STATCOM with Power Flow
- STATCOM is a second generation of FACTS device used for shunt reactive power compensation. According to the IEEE, STATCOM system is a static synchronous generator operated as a static compensator connected in parallel whose output current (inductive or capacitive) can be controlled independently of the AC system voltage [15]. The bus at which the STATCOM is connected is represented as a PV bus, this dispositive can be generated or absorbed reactive power would reach to the maximum limit. Figure.2.a shows the basic configuration of STATCOM [16].
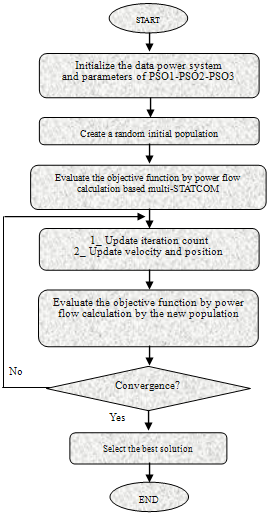 | Figure 1. Flow Chart of the proposed algorithm based three PSO variants |
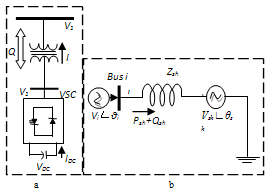 | Figure 2. a) Basic configuration of STATCOM. B) STATCOM equivalent circuit |
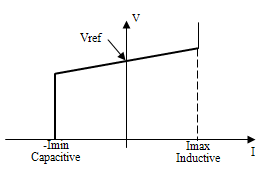 | Figure 3. Steady state control characteristics of a STACOM |
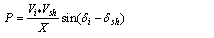 | (17) |
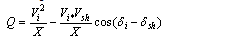 | (18) |
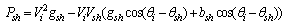 | (19) |
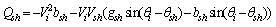 | (20) |
5. Simulation and Numerical Results
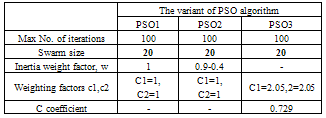
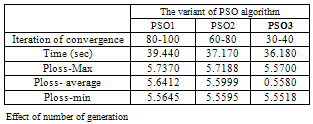
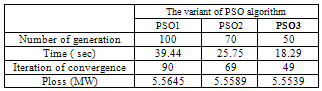
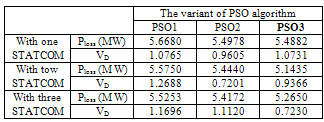
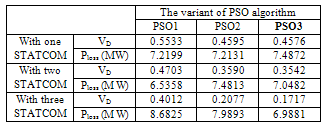
- The proposed algorithm is implemented and tested on a standard IEEE 30-Bus test system; it consists of 6 generators located at buses 1, 2, 3, 5, 8, 11, and 13, 41 branches (lines) and four transformers in line 6-9, 6-10, 4-12, and 28-27. The algorithms were implemented using the Matlab programming language; detailed analyses of the results are presented and discussed in this section. A total of three different case studies were considered, in the first case study, only to verify the effectiveness of the three PSO variant without considering the STATCOM Controllers, in case 2 the optimal reactive power is treated considering multi STATCOM and in the third case the multi objective ORPF is analysed based integration of multi STATCOM. A. Testing StrategiesCase 1: Single objective function: Ploss and VD minimization without STATCOM Controller.The main goal of this first case is to verify the feasibility and performance of the three proposed PSO variant to solve the ORPF problem. Table 1 shows the parameters of the three PSO variants. Figs 4-5-6 show the convergence characteristics of active power loss for the three PSO variants. Table.2 gives the minimum, maximum, and average optimal solution over 10 trials for different algorithms. It can be seen that the minimum cost as well as average Ploss produced by the third variant named PSO3 is better compared to the two other variants, emphasizing the better solution quality of the method.
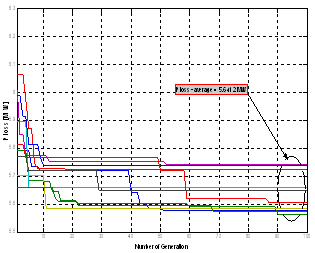 | Figure 4. Convergence characteristic of active power loss using PSO1 |
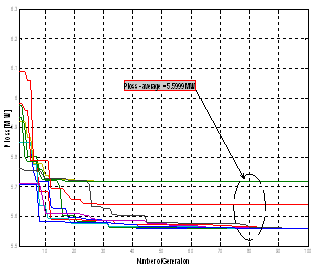 | Figure 5. Convergence characteristic of active power loss using PSO2 |
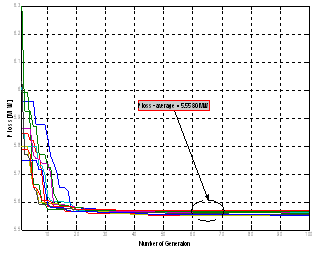 | Figure 6. Convergence characteristic of active power loss using PSO3 |
|
|
|
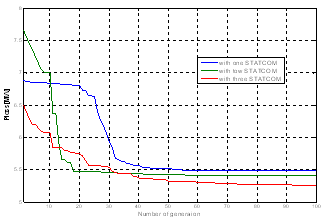 | Figure 7. Convergence characteristic of active power loss with three STATCOM |
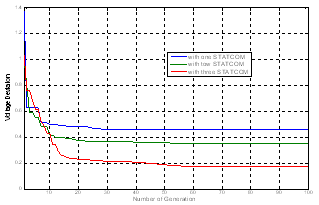 | Figure 8. Convergence characteristic of voltage deviation with three STATCOM |
|
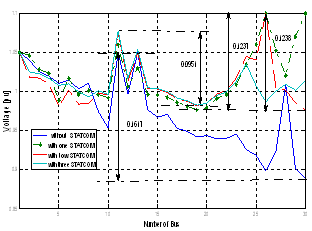 | Figure 9. Voltage profiles at all buses: IEEE 30-Bus with multi STATCOM |
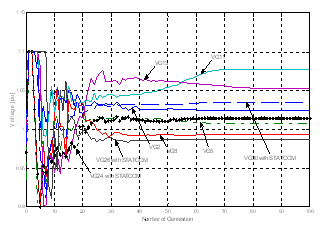 | Figure 10. Convergence characteristics of generators voltage control with PSO3 |
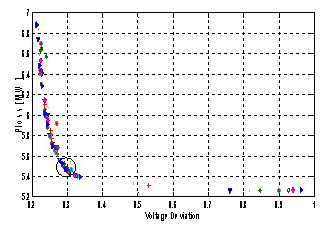 | Figure 11. Pareto optimal solution results based PSO3 |
6. Conclusions
- Multi objective optimal reactive power flow, considering multi dynamic controllers based FACTS technology is becoming one of the most important issue in power system planning and control. This paper presented the effect of the application of modified variant of PSO to adjust dynamically the voltage control of generators and the reactive power of multi STATCOM exchanged with the network considering both power loss and voltage deviation. The results demonstrated the performances of the proposed approach based PSO3 variant in term of solution quality and convergence characteristic compared to the two others variants.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML