1. Introduction

In the last few years, advances in crystal-growth techniques for the fabrication of quantum dot (QD) structure such as molecular-beam epitaxy (MBE) and chemical vapour deposition (MOCVD) have been reported [1-5]. Theoretical and experimental studies have been done on electronic and optical properties and impurity levels in structures such as quantum wells (QWs), quantum well wires and quantum dots [6-8]. The quantum dot systems GaAs/GaAlAs, GaN/AlGaN and InAs/GaAs are investigated in the present time [9-11]. Understand the electronic and optical properties of shallow impurities in CQD are important because these properties are strongly affected by the presence of impurities. With the developments of spintronics, several authors have studied the magnetic field induced metal–insulator transition [12-13]. El Ghazi et al studied the impurity binding energy of lowest-excited state in (In,Ga) -GaN spherical QD under electric field effect [14]. Sari et al [15] have studied the impurity-related optical response in cylindrical quantum dots with a δ-doped axial potential under an intense laser field. Akankan et al [16] have reported the spatial electric field effect on the self-polarization in GaAs/AlAs square quantum-well wires. It is found that impurity ground-state energy and self-polarization depend strongly on the axial component of the spatial electric field and on the coordinates of the impurity position. Zounoubi et al [17] have reported the magnetic fields effect on the polarizability of a shallow donor impurity placed of a cylindrical quantum dot (CQD). It found that the polarizability decreases as the dot radius R decreases and then increases as the radius becomes smaller. El Messaoudi et al [18] have studied the finite-barrier height effect on the polarizability of a shallow magneto-donor in a Quantum Box. They result see that for a higher and larger box, the effects of the magnetic field on the polarizability are predominant and the polarizability decrease with decreasing size of the box. Semiconductor–metal transition through diamagnetic susceptibility of a donor in a GaAs–(Ga,Al)As quantum well for both infinite and finite barrier models has been investigated by Nithiananthi et al [19]. They have also computed the diamagnetic susceptibility of a hydrogenic donor impurity in the low dimensional semiconducting systems like quantum well, quantum well wire and quantum dot. Several properties of the donors such as the polarizability and diamagnetic susceptibility are yet to be obtained [20-21]. The magnetic field effects on the diamagnetic susceptibility and binding energy of a magneto–donor in inhomogeneous quantum dot and in cylindrical quantum dot CQD have been investigated by Mmadi et al [22-23]. In the recently paper, Polaizability and diamagnetic susceptibility in the valley orbit split states in an intense field [24-25]. It’s found that for intense magnetic fields, the polarizability values decrease as the system behaves like a harmonic oscillator. In an electric field, the magnitude of the diamagnetic susceptibility values increases. Kaplana et al [26] worked the Impurity states and the diamagnetic susceptibility of a donor in a GaAs/Al_xGa_1–x As triangular quantum well under hydrostatic pressure, The results show that the diamagnetic susceptibility (χdia) of a hydrogenic donor abruptly increases at a particular pressure for 1s and 2p_± states but a steady increase for 2s state as a function of applied pressure. Their results show that the diamagnetic susceptibility increases with the magnetic field and it is more important especial for larger quantum dot. Iqraoun et al [27] reported the binding energy, polarizability and diamagnetic response of shallow donor impurity in zinc blende GaN quantum dots. It’s found that for low field strength, the binding energy is always a growing function of the radius, and for large field strengths, such physical quantity grows with the radius up to a maximum and then decreases.

Nevertheless, to the best of our knowledge, there is no study on the effect of a magnetic field on the polarizability and the diamagnetic susceptibility of a donor in Cylindrical Quantum Dot (CQD). In the present work, we investigate the calculation of the polarizability and the diamagnetic susceptibility of a donor impurity placed at the center of a CQD, with infinite barriers, as a function of the quantum sizes and for various values of the magnetic field. The organization of this paper is as follows: In Section 2, we present the basic theory; we deduce the expression of the polarizability and the diamagnetic susceptibility in the presence of a uniform magnetic field. The numerical results and discussions are reported in Section 3 with the application to a CQD made out of GaAs.

2. Hamiltonian and Basic theory

An Let us consider an impurity donor located in the center of a cylindrical Quantum dot, with radius R and length L. within the effective mass approximation the interaction of an electron with a donor impurity confined CQD, In the presence of a magnetic field B and electrical field F applied along the z direction is described bay Hamiltonian:

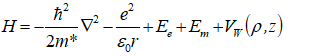(1)

where m* is the effective mass of the electron, ε₀ the dielectric constant of the CQD, e the absolute value of the electron charge, E_e=eFz the electric field, The magnetic field and where and z are the electron coordinates: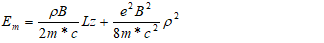

(2)

The functional form of the confinement potential energy is given by:

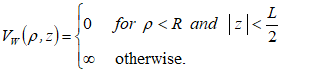(3)

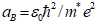By scaling all lengths in the effective Bohr radius and energies in the effective Rydberg 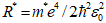. 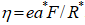is a dimensionless measure of the electric field. We can write the Hamiltonian of the impurity in cylindrical coordinates as:

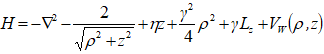(4)

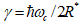where Lz is the z component of angular momentum operator in units of ħ, is a dimensionless measure of the magnetic field and 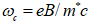the effective cyclotron frequency. Since the Schrödinger equation cannot be solved exactly, we follow the Hass variational method. The trial wave function for the calculation of the ground state energy of the system with the impurity is chosen as:

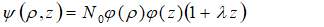(5)

Where is a variational parameter (which takes into account the presence of the weak electric field) and 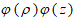is the wave function in the absence of electric field 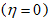given by:

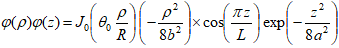(6)

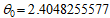where J₀ is an ordinary Bessel function of order zero; is its first zero, a and b are variational parameters and N₀ is the normalization constant.

2.1. Donor Polarizability

The polarizability of the donor confined in the CQD is defined in terms of the dipole moment by [20]

(7)

The value of that minimizes the energy expression is calculated and substituted in Eq (3)

2.2. Diamagnetic Susceptibility

The diamagnetic susceptibility of the donor impurity in CQD, in atomic unit (a.u), is given by [28]:

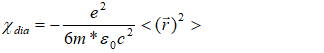(8)

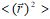Where c is the velocity of light (c = 137 and e = 1, m₀ = 1 in a.u) and is the mean square distance of the electrons from the nucleus. Thus, the corresponding energy is obtained by minimization with respect to the variational parameters a and b. The ground state donor binding energy is given by:

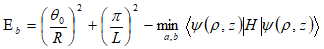(9)

The final results on the polarizability and diamagnetic susceptibility are obtained by numerical minimization of the energy expression with respect to the parameters a and b.

3. Numerical Results and Discussions

We have calculated the polarizability and the diamagnetic susceptibility of a shallow donor placed at the center of a Cylindrical Quantum Dot (CQD). We use this model to CQD’s made out of GaAs surrounded by Ga_1−xAl_xAs. In the present study we have used R^*=5.8meV, a^*=98.7A^o and ε₀=12,5. Our results for polarizability and diamagnetic susceptibility are obtained for a very small intensity of electric field (η=0,01). We begin with the plot of the binding energy as a function of the radius of the dot for tow values of length (L=1a* and L=3a*) and tow intensity values of a magnetic field (γ = 0 and γ =3) in Fig.1.

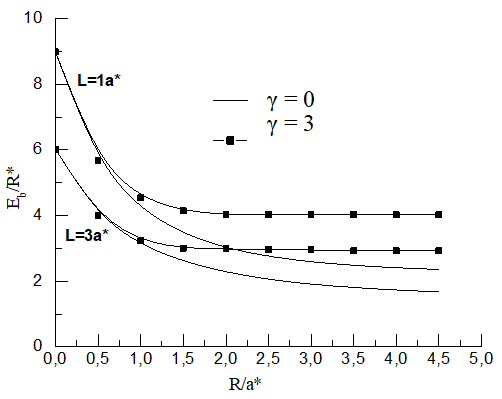Figure 1. The variation of the binding energy of a donor as function of the CQD radius for two values of the length (L=1a* and L=3a*) and two magnetic field values (γ=0 and γ=3)

As a result, we observed that the binding energy decreases when the CQD radius increases, showing that for the magnetic field (γ = 0). Beyond R=1a∗, the effect of the magnetic field begins to be apparent and the curves corresponding to the different magnetic field values tend to deviate from each other, as the radius of the point increases, reaching asymptotically the case of quantum well values. We also see that the binding energy increases with the magnetic field. In Fig.2, the polarizability α_P of a donor as a function of the radius of the cylindrical dot is reported for the infinite barrier potential case and for two values of the length CQD (L=1a* and L=3a*) and two effective magnetic field values (γ = 0 and γ =3). As a result, we have two simultaneous effects: confinement effect and the magnetic field effect. Indeed, geometric confinement effect reduces the extension of the electronic wave function which becomes more and more localized, thus reducing polarizability. We find that the donor polarizability decreases with decreasing the radii cylindrical dot and decreases with increasing the intensity of the magnetic field. Furthermore, as we have seen for energy, the effect of the magnetic field is negligible for small quantum dots and becomes predominant for large quantum dots.

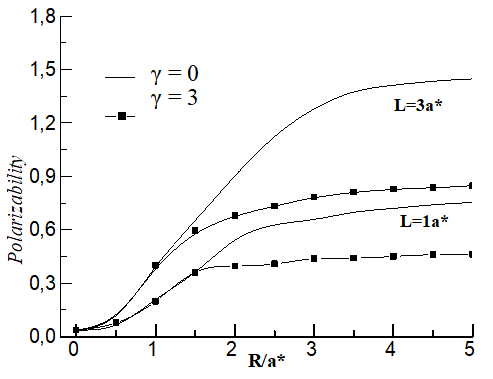Figure 2. The variation of the polarizability of the donor as a function of the dot radius for two magnetic field (γ=0 and γ=3) and two values of the length L=1a* and L=3a*

In Fig.3 we reported the polarizability versus he effective magnetic γ field for three radius values (R=1a*, R=3a*, R=5a* and the length L=3a*). We remark that the polarizability α becomes more important for large values R and decreases at increasing magnetic. For a strong magnetic field (γ > 2) and for large CQD dot (R>3a*) the two upper curves coincide, so the spatial confinement is negligible and the magnetic field effects are predominant.

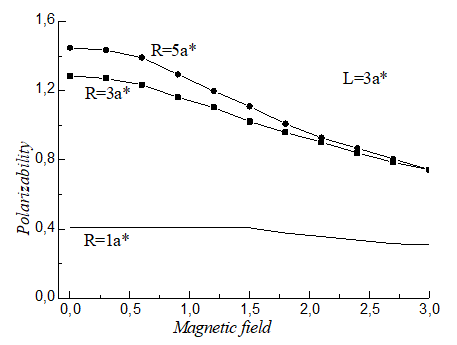Figure 3. Variation of the polarizability αP function of magnetic field γ for three values radius (R=1a*, R=3a* and R=5a*) with L=3a*

We present in Fig.4, the effects of the magnetic field influence on the diamagnetic susceptibility as a function of the radius R for two magnetic field values (γ=0 and (γ=3) and (L=1a* and L=3a*). The results of this figure show that in the presence of the magnetic field the diamagnetic susceptibility remains almost constant in the case of large CQD. Nevertheless, for weak axial confinement (L>1a*) and Beyond R=1a∗, the diamagnetic susceptibility decreases with the increase of CQD length.

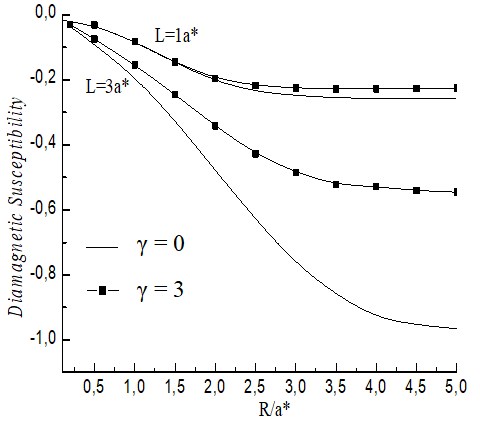Figure 4. The variation of the diamagnetic susceptibility as function of the CQD radius for two values of the length (L=1a* and L=3a*) and two magnetic field values (γ=0 and γ=3)

It’s tend to the three dimensional value (-1.1a.u) which correspond to the bulk limit case (see references [29,30]). Also the diamagnetic susceptibility increases with magnetic field. This increase is due to a decrease in charge distribution when an external magnetic field is applied. We have reported in Fig.5 the variation of diamagnetic susceptibility ꓫ_dia as a function of the magnetic field for three cylindrical quantum dot radius (R=1a*, 3a*and R=5a*) and L=3a. We remark that the magnetic field effect on the diamagnetic susceptibility is more dominant for small magnetic field values and this effect is not significant especially for large magnetic field values. We observe that diamagnetic susceptibility strongly depends on the intensity of the magnetic field which narrows the atomic orbital of the donor electron and increases its susceptibility. The deviations between the diamagnetic susceptibility curves decrease as the magnetic field increases.

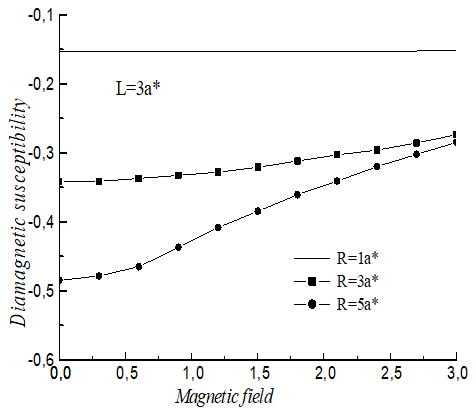Figure 5. Variation of the diamagnetic susceptibility χdia function of magnetic field for three values radius (R=1a*, R=3a* and R=5a*) with L=3a*

4. Conclusions

In this study, we have presented the magnetic field influence on the polarizability and on the diamagnetic susceptibility of a shallow donor in a GaAs Cylindrical Quantum Dot (CQD). The magnetic field effect is appreciable especially for large CQD width is. The polarizability and the diamagnetic susceptibility depend strongly on the geometrical confinement. The effects of the electron–phonon interactions on the polarizability and diamagnetic susceptibility of a magneto-donor in CQD are in progress.

ACKNOWLEDGEMENTS

Izeddine Zorkani, and Ali Mmadi would like to thank the Abdus Salam International Centre for Theoretical Physics.