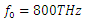-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Electromagnetics and Applications
p-ISSN: 2168-5037 e-ISSN: 2168-5045
2019; 9(1): 14-34
doi:10.5923/j.ijea.20190901.03

Optimization of Optical Parametric Amplification Efficiency in a Microresonator Under Ultrashort Pump Wave Excitation
Özüm Emre Aşırım, Mustafa Kuzuoğlu
Department of Electrical and Electronics Engineering, Middle East Technical University, Ankara, Turkey
Correspondence to: Özüm Emre Aşırım, Department of Electrical and Electronics Engineering, Middle East Technical University, Ankara, Turkey.
| Email: |  |
Copyright © 2019 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

This paper aims to computationally show that it is possible to achieve wideband high-gain optical parametric amplification in a very small low-loss microcavity. Our model involves numerical modeling of the charge polarization density in terms of the nonlinear electron cloud motion. Through a series of finite difference time domain simulations, we have determined the pump wave frequencies that maximize the electric energy density inside the microcavity. These pump wave frequencies that maximize the energy density are then selected for stimulus (input) wave amplification via nonlinear energy coupling. The achieved amplification factors are tabulated in terms of the pump wave frequency, stored electric energy density, and the intracavity charge polarization density. It is found that unlike what the current literature on nonlinear wave mixing suggests, micrometer-scale achievement of wideband high-gain optical parametric amplification is possible by choosing the optimum pump wave frequency that maximizes the stored electric energy density.
Keywords: Optical amplification, Nonlinear wave mixing, Optical microcavity, Parametric amplifier, Optimization
Cite this paper: Özüm Emre Aşırım, Mustafa Kuzuoğlu, Optimization of Optical Parametric Amplification Efficiency in a Microresonator Under Ultrashort Pump Wave Excitation, International Journal of Electromagnetics and Applications, Vol. 9 No. 1, 2019, pp. 14-34. doi: 10.5923/j.ijea.20190901.03.
Article Outline
1. Introduction
- Electromagnetic wave amplification by nonlinear wave mixing has been studied extensively in the context of nonlinear optics [1]. It has been well established that we can amplify a relatively low power input wave, by using another wave of high intensity, which is called the pump wave, in a nonlinear medium [2]. The theory of electromagnetic wave amplification via nonlinear wave mixing involves the transfer of energy from the pump wave to the input wave as a result of nonlinear coupling in a medium that exhibits a strong nonlinear response under excitation [3]. The nonlinear wave mixing theory has been mostly investigated experimentally rather than computationally, especially for wave amplification purposes. The most important reason behind this trend is that, this concept is almost always studied in the micrometer or nanometer wavelength range, and yet the required medium length to observe any significant nonlinear effect is in the milimeter or centimeter range, which requires an extremely high computational cost for obtaining meaningful results, particularly for the purpose of wave amplification.Furthermore, based on the current concept of wave amplification via nonlinear wave mixing a.k.a parametric amplification, it is impossible to achieve a non-negligible wave amplification in a few micron sized gain medium or a cavity. The required gain medium length for significant parametric amplification is mostly on the order of centimeters [4]. For this reason, the concept of parametric amplification is not feasible to be used for optical microsystems. In this paper, we have carried out a computational analysis that aims to show that it is possible to amplify a low power stimulus wave by mixing it with an intense pump wave of very short duration, in a wide range of frequencies and with a very large gain coefficient, inside a low-loss micro-cavity of several micrometers of length, by maximizing the stored pump wave energy in the cavity.We will first discuss about high energy storage in low-loss cavities. A low-loss cavity has a high quality factor, which is a measure of the energy storage capability of a cavity. Then, we will discuss about wave propagation in nonlinear dispersive media, and formulate our problem along with it’s finite difference time domain implementation. Finally, we will present our results through a set of simulations and we will try to depict that a very high gain optical parametric amplification is possible in a low-loss micro-cavity, when the correct pump wave frequencies that maximize the stored intracavity energy are chosen.
2. Intracavity Energy Density and the Cavity Quality (Q) Factor
- The Q factor is a measure of the energy storage capability of a cavity. A high Q value means that high energy can be stored in the cavity. It depends on the length of the cavity, the values of the reflection coefficients of the cavity walls, the frequency of the wave that is propagating inside the cavity, the total absorption coefficient of the medium between the cavity walls, and any kind of diffraction or scattering loss that can occur inside a cavity [14-16]. The Q factor of a cavity is defined as
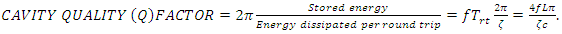 | (1) |
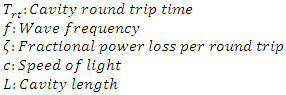 The stored electric energy density in a medium depends on both the intensity of the electric field excitation, and the electric charge polarization density of the medium. Assuming a one dimensional analysis, the stored electric energy density in an isotropic medium is defined as [3]
The stored electric energy density in a medium depends on both the intensity of the electric field excitation, and the electric charge polarization density of the medium. Assuming a one dimensional analysis, the stored electric energy density in an isotropic medium is defined as [3]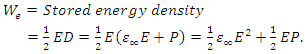 | (2) |
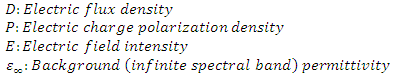 As an example case in which a very high energy can be stored inside a cavity, involves a dispersive medium, which has a frequency dependent permittivity as stated below [5]
As an example case in which a very high energy can be stored inside a cavity, involves a dispersive medium, which has a frequency dependent permittivity as stated below [5]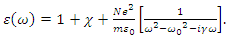 | (3) |
 If
If  then we can write [2]
then we can write [2]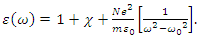 | (4) |
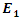 and
and 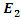 . Let us assume that the angular frequency
. Let us assume that the angular frequency 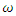 of
of 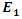 is almost equal to the resonance frequency of the medium
is almost equal to the resonance frequency of the medium 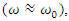 then the stored energy in this cavity becomes extremely high. Now assume that
then the stored energy in this cavity becomes extremely high. Now assume that 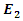 has a significantly different frequency than the resonance frequency of the medium. Unless it has a very high power,
has a significantly different frequency than the resonance frequency of the medium. Unless it has a very high power, 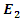 will not yield a noticeable energy increase in the cavity as it’s frequency is not almost equal to the resonance frequency. Furthermore,
will not yield a noticeable energy increase in the cavity as it’s frequency is not almost equal to the resonance frequency. Furthermore, 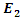 will not be able to absorb any energy from the energized cavity as there is no energy coupling mechanism, simply because the medium is linear. To account for an energy transfer from an energized cavity to a low power wave, we need a nonlinear wave propagation analysis between the cavity walls, and for nonlinearity to arise, either the medium itself must be highly nonlinear, or at least one of the waves that propagate inside the cavity must have a very high amplitude.
will not be able to absorb any energy from the energized cavity as there is no energy coupling mechanism, simply because the medium is linear. To account for an energy transfer from an energized cavity to a low power wave, we need a nonlinear wave propagation analysis between the cavity walls, and for nonlinearity to arise, either the medium itself must be highly nonlinear, or at least one of the waves that propagate inside the cavity must have a very high amplitude.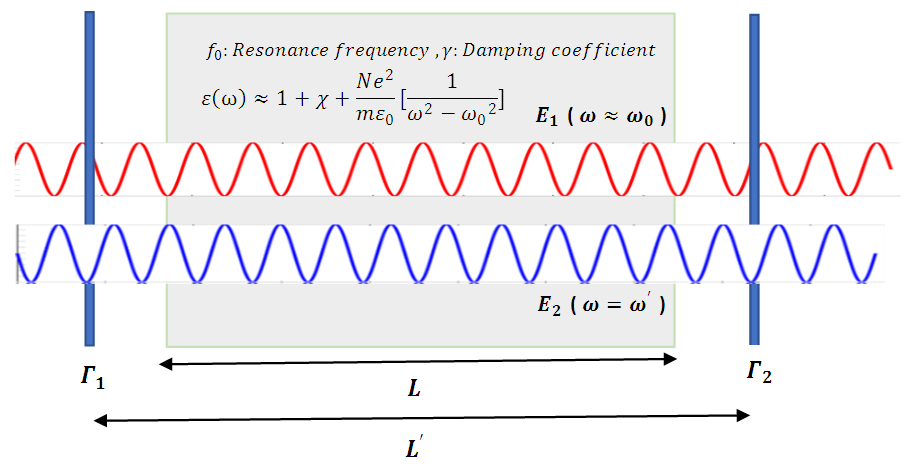 | Figure 1. A cavity with a high electric energy density (due to 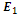 ) and two propagating waves ) and two propagating waves |
3. Wave Propagation in Nonlinear Dispersive Media
- Nonlinearity arises when at least one of the waves that propagate in a medium have a very high intensity. Such high intensities are only possible with very short duration pulses [6,8], such as the pulses of a mode locked laser, which have durations on the scale of picoseconds or femtoseconds [7,9,10]. When high intensity pulses have very short durations, which is almost always the case, we have to account for the wave dispersion, as the impulse response of the charge polarization density of many dielectric media last much longer in duration than the pulse durations of such high intensity pulses. One can solve the wave equation in parallel with the nonlinear equation of motion of the electron cloud for a nonlinear dispersive medium. This is because the parameters such as the resonance frequency, damping coefficient, atom density, and atomic diameter have known values for most solids, which makes the simulation results much more meaningful and precise. In order to determine the time variation of the electric field in a nonlinear dispersive medium, we need to solve the following two equations [1]:
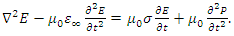 | (5) |
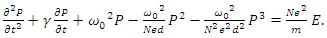 | (6) |
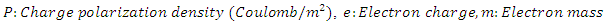 In Eq. (6) we have made an expansion up to the third order of the nonlinear charge polarization density as higher order terms will be negligibly small. For a dielectric medium, the electrical conductivity can be assumed as negligible
In Eq. (6) we have made an expansion up to the third order of the nonlinear charge polarization density as higher order terms will be negligibly small. For a dielectric medium, the electrical conductivity can be assumed as negligible 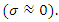 Some typical values for solid dielectric media are [1]
Some typical values for solid dielectric media are [1] 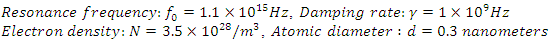
 | Figure 2. A nonlinear dipersive medium placed in a cavity |
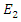 that has a very high amplitude, without the presence of the low amplitude wave
that has a very high amplitude, without the presence of the low amplitude wave 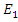 , the pair of equations that describe the propagation of
, the pair of equations that describe the propagation of 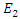 in a nonlinear dispersive medium is given as
in a nonlinear dispersive medium is given as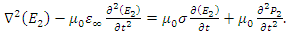 | (7a) |
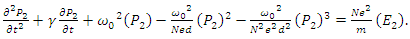 | (7b) |
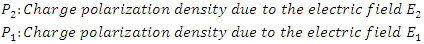 Now assume that
Now assume that 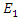 and
and 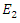 are propagating together in the same nonlinear dispersive medium, in this case the pair of equations that represent the total electric field propagation is given as
are propagating together in the same nonlinear dispersive medium, in this case the pair of equations that represent the total electric field propagation is given as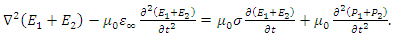 | (8a) |
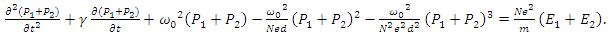 | (8b) |
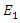 in the presence of the high amplitude wave
in the presence of the high amplitude wave 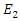 , in other words we want to determine the propagation of
, in other words we want to determine the propagation of 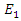 when there is an energy coupling from
when there is an energy coupling from 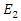 as a result of the nonlinear interaction. In order to do that we subtract equations (7a,7b) from equations (8a,8b) respectively, which gives us
as a result of the nonlinear interaction. In order to do that we subtract equations (7a,7b) from equations (8a,8b) respectively, which gives us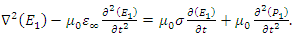 | (9a) |
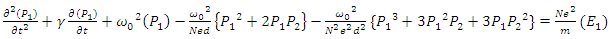 | (9b) |
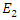 and
and 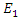 are coupled to each other. Based on equations (9a,9b), we will investigate whether it is possible to amplify the low power electric field
are coupled to each other. Based on equations (9a,9b), we will investigate whether it is possible to amplify the low power electric field 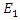 , by drawing energy from a low loss cavity that is energized by the high power electric field
, by drawing energy from a low loss cavity that is energized by the high power electric field 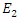 .
.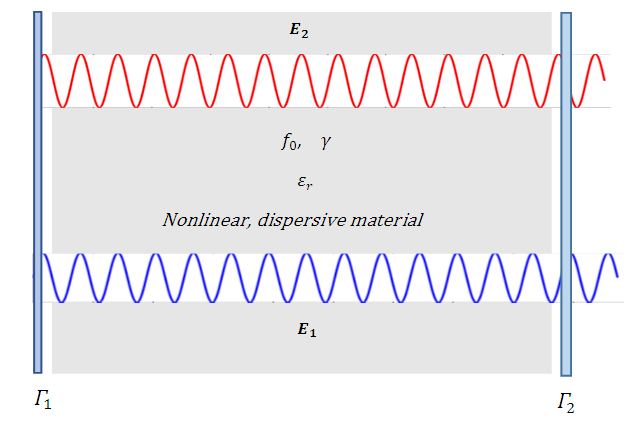 | Figure 3. Two waves are propagating through a nonlinear dipersive medium placed in a cavity |
3.1. Finite Difference Time Domain Formulation of Energy Coupling in a Nonlinear Dispersive Medium
- As introduced in the previous section,
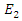 is the high power wave that initiates the nonlinear energy coupling process and
is the high power wave that initiates the nonlinear energy coupling process and 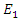 is the low power wave that will absorb energy from
is the low power wave that will absorb energy from 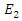 . The finite difference time domain formulation of this process in a low-loss dispersive cavity requires the discretization of equations (7a,7b) and (9a,9b). Here we assume a one dimensional space along the x direction so that
. The finite difference time domain formulation of this process in a low-loss dispersive cavity requires the discretization of equations (7a,7b) and (9a,9b). Here we assume a one dimensional space along the x direction so that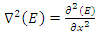 | (10) |
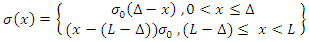 | (11a) |
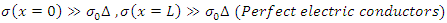 | (11b) |
 | Figure 4. The domain of computation and the domain of termination (PML region) |
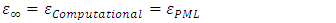 | (12a) |
 | (12b) |
 | (13a) |
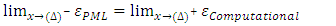 | (13b) |
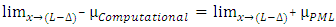 | (13c) |
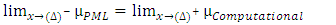 | (13d) |
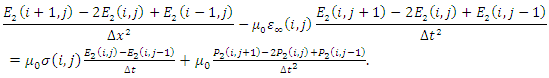 | (14) |
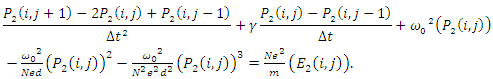 | (15) |
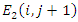 i.e. the value of
i.e. the value of 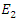 at a given point at the next time step. Since
at a given point at the next time step. Since 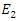 is coupled to
is coupled to 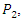 we first solve for
we first solve for 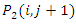 and then substitute it into the equation for
and then substitute it into the equation for 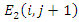 . We keep on solving these two equations iteratively for all time steps and for all points in the spatial domain of a given one dimensional problem. For a higher accuracy of the resulting solution, we choose
. We keep on solving these two equations iteratively for all time steps and for all points in the spatial domain of a given one dimensional problem. For a higher accuracy of the resulting solution, we choose 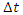 and
and 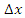 as small as possible [19,20]. Now we discretize equations (9a,9b) and substitute the value of
as small as possible [19,20]. Now we discretize equations (9a,9b) and substitute the value of 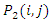 obtained from equations (7a,7b)
obtained from equations (7a,7b)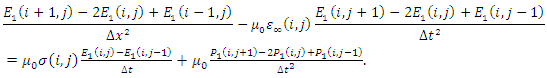 | (16a) |
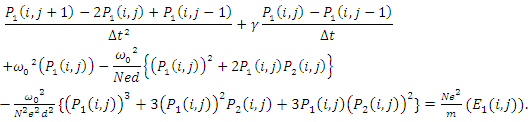 | (16b) |
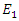 and
and 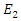 at any point in one dimensional space. In order to test our computational model, we have compared our computational results with the theoretical results in the well established context of nonlinear sum frequency generation in the appendix section. Now we move on to the simulation results.
at any point in one dimensional space. In order to test our computational model, we have compared our computational results with the theoretical results in the well established context of nonlinear sum frequency generation in the appendix section. Now we move on to the simulation results.4. Simulation Results
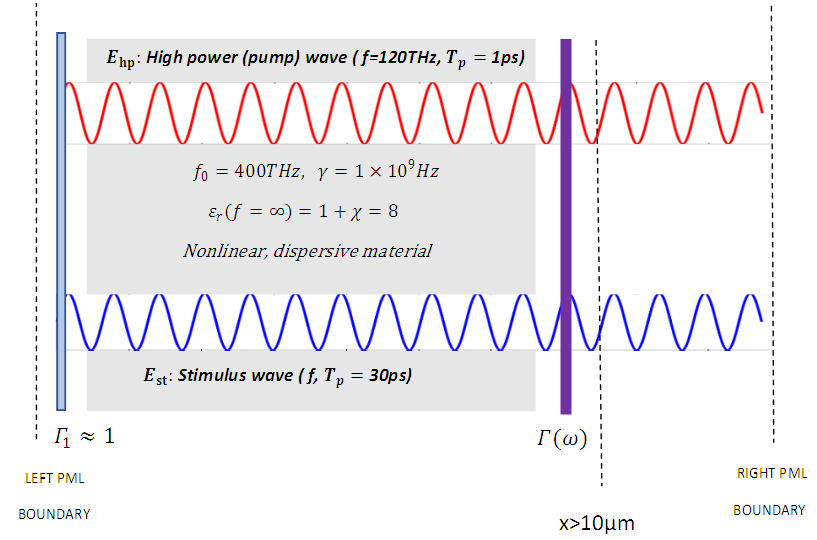
- Simulation 1 - Part 1: Sweeping the pump wave frequency to maximize the intracavity energy densityAssume that a 250THz infrared stimulus wave
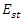 and a high power pump wave
and a high power pump wave 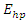 (frequency to be determined) are propagating inside a low-loss (high Q) cavity that has two reflecting walls. The reflecting wall on the left side can be thought as an optical isolator and has a reflection coefficient of
(frequency to be determined) are propagating inside a low-loss (high Q) cavity that has two reflecting walls. The reflecting wall on the left side can be thought as an optical isolator and has a reflection coefficient of 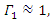 the one on the right side represents a switch controlled optical band-pass filter with a frequency dependent reflection coefficient
the one on the right side represents a switch controlled optical band-pass filter with a frequency dependent reflection coefficient 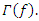 Both waves are generated at x=0𝜇m and at the time instant t=0. The waves and the parameters of the gain medium are as given below:
Both waves are generated at x=0𝜇m and at the time instant t=0. The waves and the parameters of the gain medium are as given below: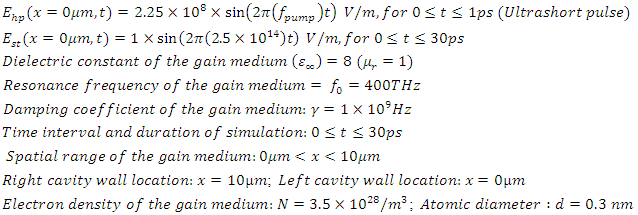
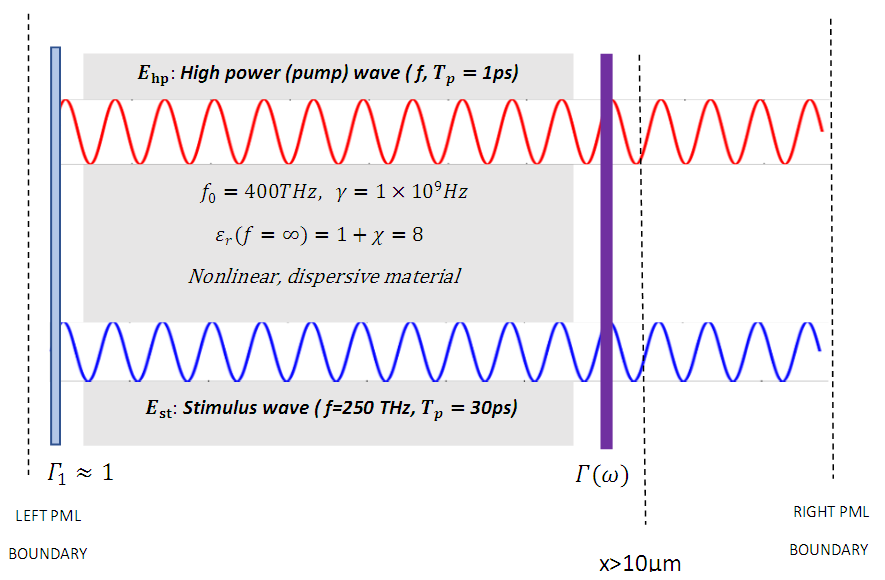 | Figure 5. Configuration of the cavity and the dielectric material specifications for simulation1-part1 |
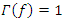 for all
for all 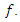 The filter is used for post-processing of the results. Our problem: Find the optimum pump wave frequency
The filter is used for post-processing of the results. Our problem: Find the optimum pump wave frequency 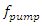 that maximizes
that maximizes 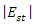 in the cavity, for
in the cavity, for 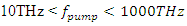 (THz to UV), for
(THz to UV), for  such that
such that 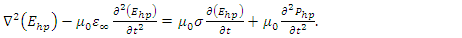 | (7a) |
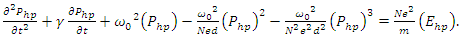 | (7b) |
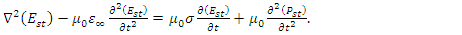 | (9a) |
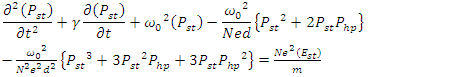 | (9b) |
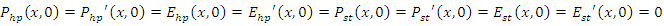 Boundary and excitation conditions:
Boundary and excitation conditions: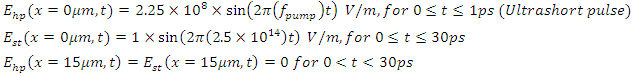 Absorbing boundary condition (perfectly matched layer):
Absorbing boundary condition (perfectly matched layer):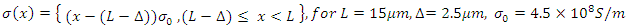 Optical isolator condition: Full reflection at
Optical isolator condition: Full reflection at 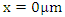
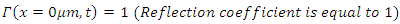 Switch controlled optical bandpass filter condition: Full reflection at
Switch controlled optical bandpass filter condition: Full reflection at 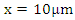 for t≤30 picoseconds, frequency dependent reflection at
for t≤30 picoseconds, frequency dependent reflection at 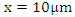 after t=30 picoseconds;
after t=30 picoseconds;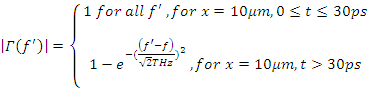 If amplified, the stimulus wave at t=30 picoseconds will not be monochromatic anymore, this will be due to the spectral broadening inside the cavity [11-13]. However, by adjusting the center frequency of the band-pass filter to be 250THz, we will get an amplified quasi-monochromatic output. The pump wave frequency will be varied from 10THz to 1000THz in 10THz increments and a pump wave frequency that yields a strong amplification of the stimulus wave will be chosen. The electric energy density
If amplified, the stimulus wave at t=30 picoseconds will not be monochromatic anymore, this will be due to the spectral broadening inside the cavity [11-13]. However, by adjusting the center frequency of the band-pass filter to be 250THz, we will get an amplified quasi-monochromatic output. The pump wave frequency will be varied from 10THz to 1000THz in 10THz increments and a pump wave frequency that yields a strong amplification of the stimulus wave will be chosen. The electric energy density 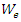 and the charge polarization density
and the charge polarization density 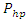 created by the pump wave, are plotted with respect to the pump wave frequency in Fig. 6 and Fig. 7 respectively. Stimulus wave amplitude gain versus pump wave frequency plot is shown in Fig. 8.
created by the pump wave, are plotted with respect to the pump wave frequency in Fig. 6 and Fig. 7 respectively. Stimulus wave amplitude gain versus pump wave frequency plot is shown in Fig. 8. | Figure 6. Maximum electric energy density created by the pump wave (for 0<t<30ps), as measured inside the cavity at x=5.73µm, versus the frequency of the pump wave |
 | Figure 7. Maximum charge polarization density created by the pump wave (for 0<t<30ps), as measured inside the cavity at x=5.73µm, versus the frequency of the pump wave |
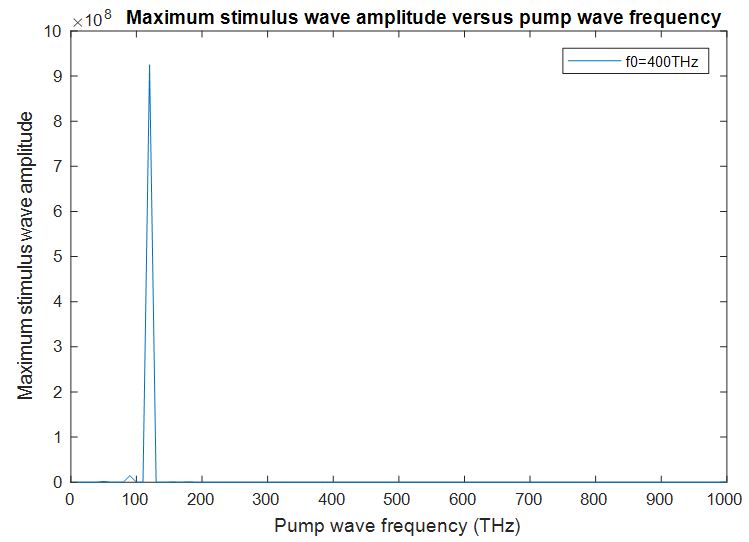 | Figure 8. Maximum stimulus wave amplitude between 0<t<30ps, as measured inside the cavity at x=5.73µm, versus the frequency of the pump wave |
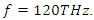 The peak polarization density
The peak polarization density 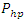 created by the pump wave (which acts as the coupling coefficient), is high at this frequency. The peak electric energy density
created by the pump wave (which acts as the coupling coefficient), is high at this frequency. The peak electric energy density 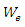 created by the pump wave is also high at
created by the pump wave is also high at 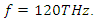 Therefore we have an amplification peak at
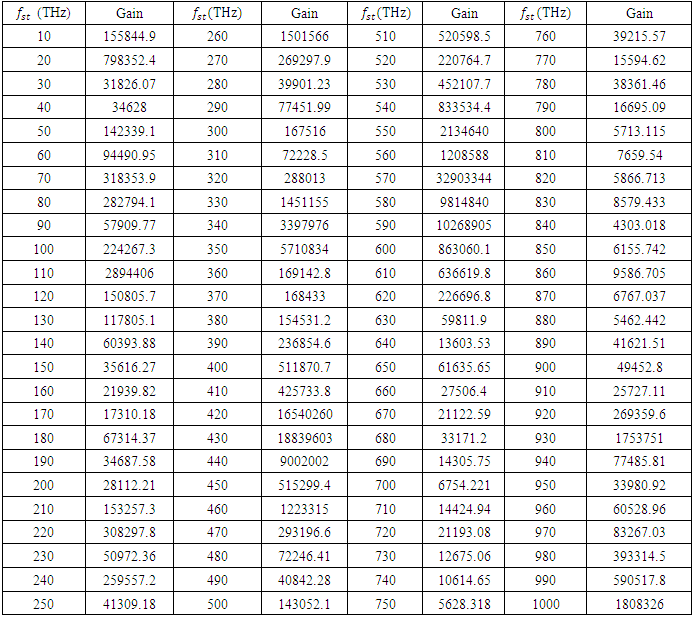
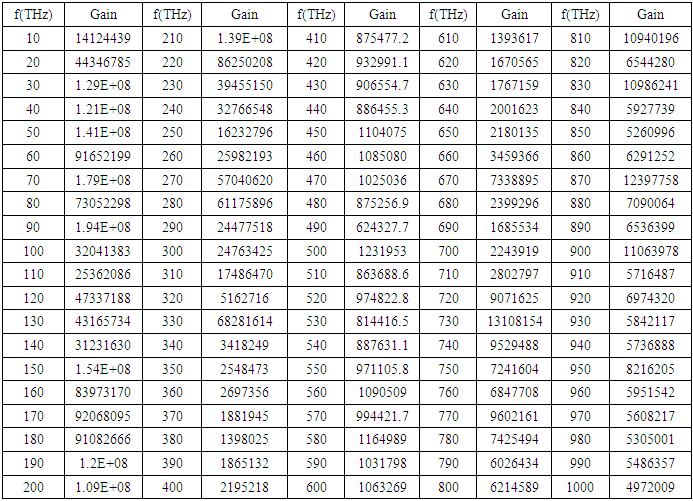
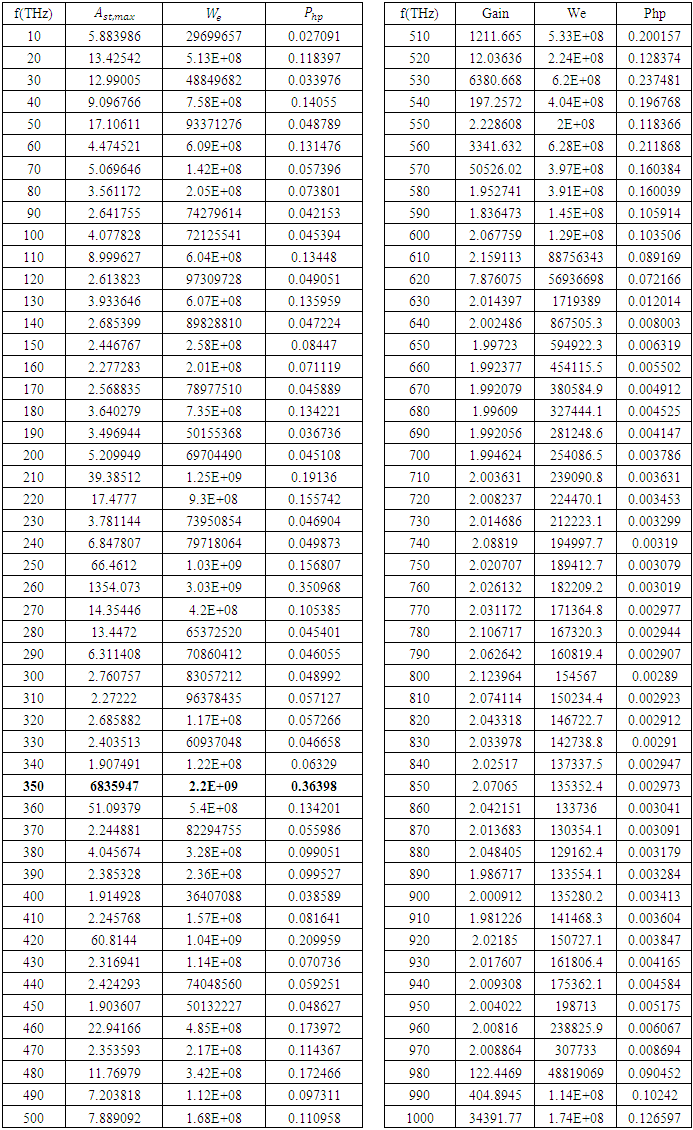
Therefore we have an amplification peak at 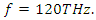 The same is true for all other peaks. If we have a look at Table 1, wherever the electric energy density and the polarization density created by the pump wave, are high, there is a stronger stimulus wave amplification.
The same is true for all other peaks. If we have a look at Table 1, wherever the electric energy density and the polarization density created by the pump wave, are high, there is a stronger stimulus wave amplification. 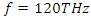 maximizes the intra-cavity energy and amplifies the stimulus wave, we choose this frequency as the frequency of pump wave excitation in order to compute the amplification (gain) spectrum of the stimulus wave. However, as already mentioned, the amplified stimulus wave is not monochromatic anymore due to the spectral broadening inside the cavity. Therefore, we must make a seperate analysis to obtain the gain spectrum of the stimulus wave, under a 120THz pump wave excitation.
maximizes the intra-cavity energy and amplifies the stimulus wave, we choose this frequency as the frequency of pump wave excitation in order to compute the amplification (gain) spectrum of the stimulus wave. However, as already mentioned, the amplified stimulus wave is not monochromatic anymore due to the spectral broadening inside the cavity. Therefore, we must make a seperate analysis to obtain the gain spectrum of the stimulus wave, under a 120THz pump wave excitation. 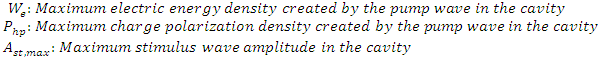
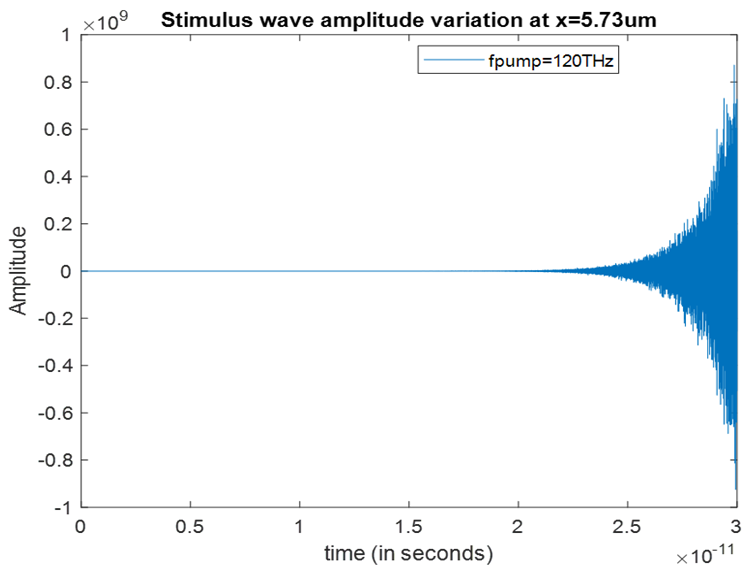 | Figure 9. Stimulus wave amplitude variation at x=5.73µm for a pump wave frequency of 120THz |
 | Figure 10. The configuration for computing the gain spectrum of the stimulus wave for 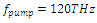 |
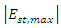 in the cavity for each stimulus wave frequency
in the cavity for each stimulus wave frequency 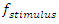 , in the range
, in the range 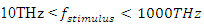 (THz to UV), for
(THz to UV), for 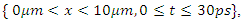 such that
such that 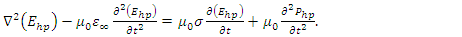 | (7a) |
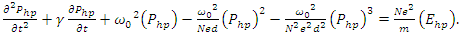 | (7b) |
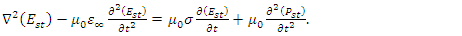 | (9a) |
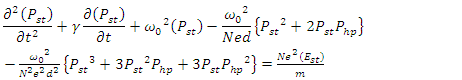 | (9b) |
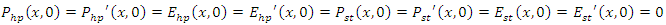 Boundary conditions:
Boundary conditions: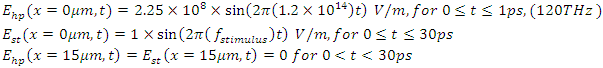 Absorbing boundary condition (perfectly matched layer):
Absorbing boundary condition (perfectly matched layer):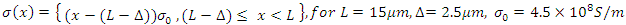 Optical isolator condition: Full reflection at
Optical isolator condition: Full reflection at 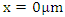
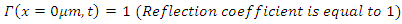 Switch controlled optical bandpass filter condition: Full reflection at
Switch controlled optical bandpass filter condition: Full reflection at 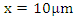 for
for 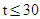 picoseconds, frequency dependent reflection at
picoseconds, frequency dependent reflection at 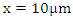 after t=30 picoseconds. For a given stimulus wave frequency (f), the magnitude frequency response of the filter is chosen to be
after t=30 picoseconds. For a given stimulus wave frequency (f), the magnitude frequency response of the filter is chosen to be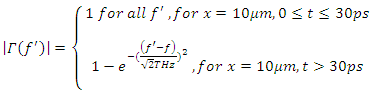 The amplification spectrum of the stimulus wave for
The amplification spectrum of the stimulus wave for 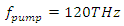 is tabulated below in Table 2. The stimulus wave is supplied to the cavity at t=0 as a quasi-monochromatic wave. For a given initial (at t=0) stimulus wave frequency, the center frequency of the band-pass filter is adjusted to be at the same frequency with the initial stimulus wave frequency. By doing so, we can observe how much gain can be obtained from the cavity for each initial stimulus wave frequency. We choose the pump wave frequency as
is tabulated below in Table 2. The stimulus wave is supplied to the cavity at t=0 as a quasi-monochromatic wave. For a given initial (at t=0) stimulus wave frequency, the center frequency of the band-pass filter is adjusted to be at the same frequency with the initial stimulus wave frequency. By doing so, we can observe how much gain can be obtained from the cavity for each initial stimulus wave frequency. We choose the pump wave frequency as 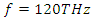 as it maximizes the amplification, and we sweep the stimulus wave frequency from 10THz to 1000THz in 10THz increments.
as it maximizes the amplification, and we sweep the stimulus wave frequency from 10THz to 1000THz in 10THz increments.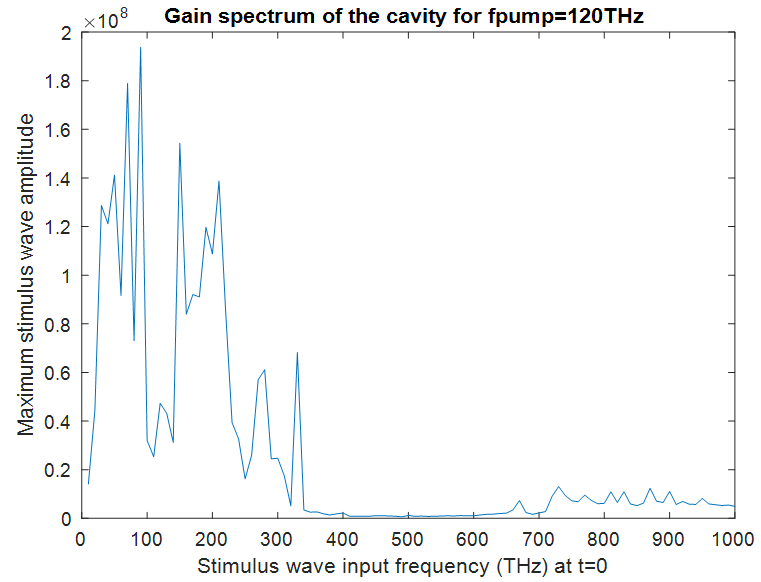 | Figure 11. Gain spectrum of the stimulus wave for 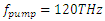 and and 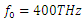 |
|
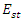 and a high power pump wave
and a high power pump wave 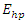 (frequency to be determined) are propagating inside a low-loss (high Q) cavity that has two reflecting walls. The reflecting wall on the left side can be thought as an optical isolator and has a reflection coefficient of
(frequency to be determined) are propagating inside a low-loss (high Q) cavity that has two reflecting walls. The reflecting wall on the left side can be thought as an optical isolator and has a reflection coefficient of 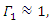 the one on the right side represents a switch controlled optical band-pass filter with a frequency dependent reflection coefficient
the one on the right side represents a switch controlled optical band-pass filter with a frequency dependent reflection coefficient 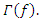 Both waves are generated at x=0𝜇m and at the time instant t=0. The waves and the parameters of the gain medium are as given below:
Both waves are generated at x=0𝜇m and at the time instant t=0. The waves and the parameters of the gain medium are as given below:
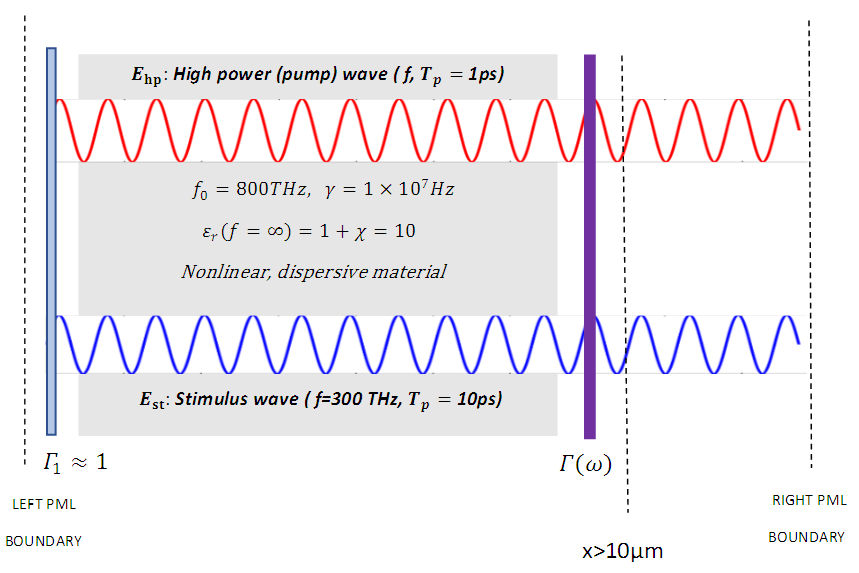 | Figure 12. Configuration of the cavity and the dielectric material specifications for simulation2-part1 |
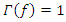 for all
for all 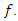 The filter is used for post-processing of the results. Our problem: Find the optimum pump wave frequency
The filter is used for post-processing of the results. Our problem: Find the optimum pump wave frequency 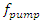 that maximizes
that maximizes 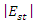 in the cavity, for
in the cavity, for 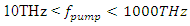 (THz to UV), for
(THz to UV), for 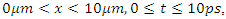 such that
such that 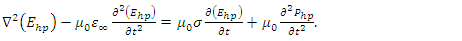 | (7a) |
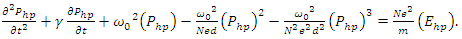 | (7b) |
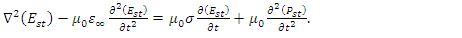 | (9a) |
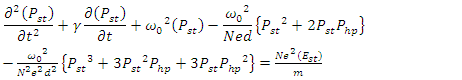 | (9b) |
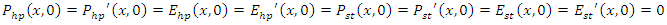 Boundary and excitation conditions:
Boundary and excitation conditions: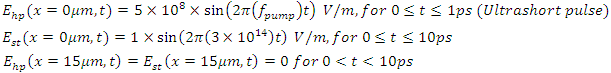 Absorbing boundary condition (perfectly matched layer):
Absorbing boundary condition (perfectly matched layer):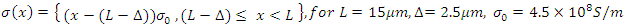 Optical isolator condition: Full reflection at
Optical isolator condition: Full reflection at 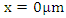
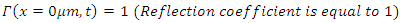 Switch controlled optical bandpass filter condition: Full reflection at
Switch controlled optical bandpass filter condition: Full reflection at 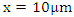 for
for 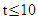 picoseconds, frequency dependent reflection at
picoseconds, frequency dependent reflection at 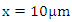 after t=10 picoseconds;
after t=10 picoseconds;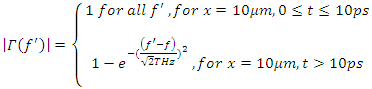 If amplified, the stimulus wave at t=10 picoseconds will not be monochromatic anymore, this will be due to the spectral broadening inside the cavity. However, by adjusting the center frequency of the band-pass filter to be 300THz, we will get an amplified quasi-monochromatic output. The pump wave frequency will be varied from 10THz to 1000THz in 10THz increments and a pump wave frequency that yields a strong amplification of the stimulus wave will be chosen. The electric energy density
If amplified, the stimulus wave at t=10 picoseconds will not be monochromatic anymore, this will be due to the spectral broadening inside the cavity. However, by adjusting the center frequency of the band-pass filter to be 300THz, we will get an amplified quasi-monochromatic output. The pump wave frequency will be varied from 10THz to 1000THz in 10THz increments and a pump wave frequency that yields a strong amplification of the stimulus wave will be chosen. The electric energy density  and the charge polarization density
and the charge polarization density  created by the pump wave, are plotted with respect to the pump wave frequency in Fig. 13 and Fig. 14 respectively. Stimulus wave amplitude gain versus pump wave frequency plot is shown in Fig. 15.
created by the pump wave, are plotted with respect to the pump wave frequency in Fig. 13 and Fig. 14 respectively. Stimulus wave amplitude gain versus pump wave frequency plot is shown in Fig. 15.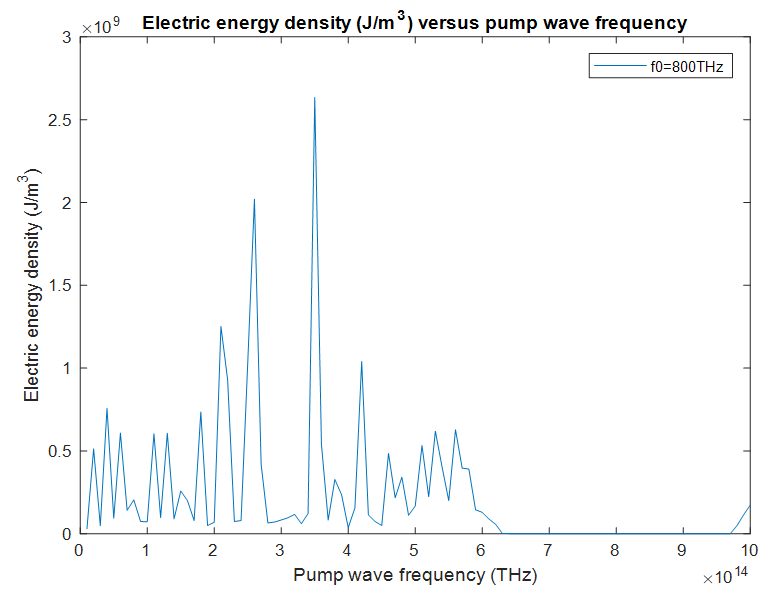 | Figure 13. Maximum electric energy density created by the pump wave (for 0<t<10ps), as measured inside the cavity at x=5.73µm, versus the frequency of the pump wave |
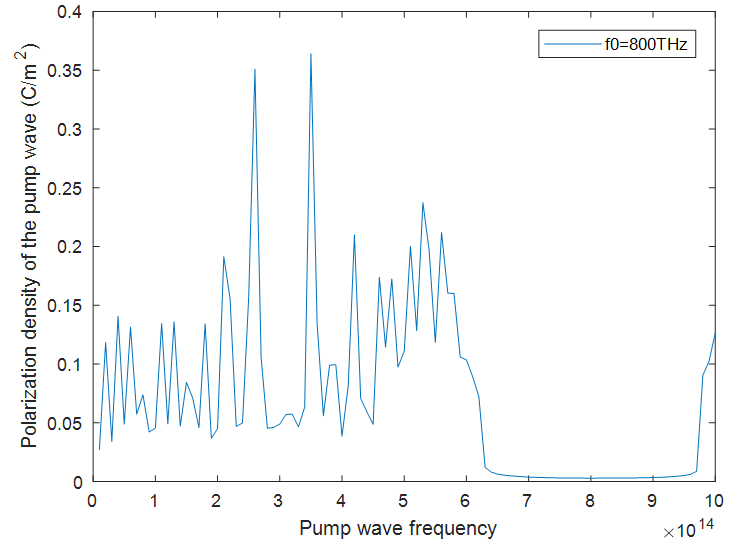 | Figure 14. Maximum charge polarization density created by the pump wave (for 0<t<10ps), as measured inside the cavity at x=5.73µm, versus the frequency of the pump wave |
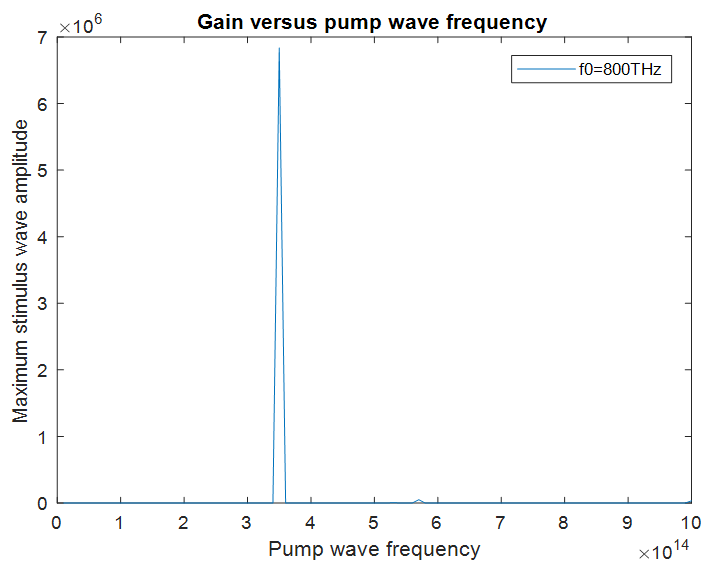 | Figure 15. Maximum stimulus wave amplitude between 0<t<10ps, as measured inside the cavity at x=5.73µm, versus the frequency of the pump wave |
 The peak polarization density
The peak polarization density  created by the pump wave (which acts as the coupling coefficient), is high at this frequency. The peak electric energy density
created by the pump wave (which acts as the coupling coefficient), is high at this frequency. The peak electric energy density 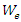 created by the pump wave is also high at
created by the pump wave is also high at 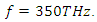 Therefore we have an amplification peak at
Therefore we have an amplification peak at 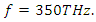 The same is true for all other peaks. If we have a look at Table 3, wherever the electric energy density and the polarization density created by the pump wave, are high, there is a stronger stimulus wave amplification.
The same is true for all other peaks. If we have a look at Table 3, wherever the electric energy density and the polarization density created by the pump wave, are high, there is a stronger stimulus wave amplification.
|
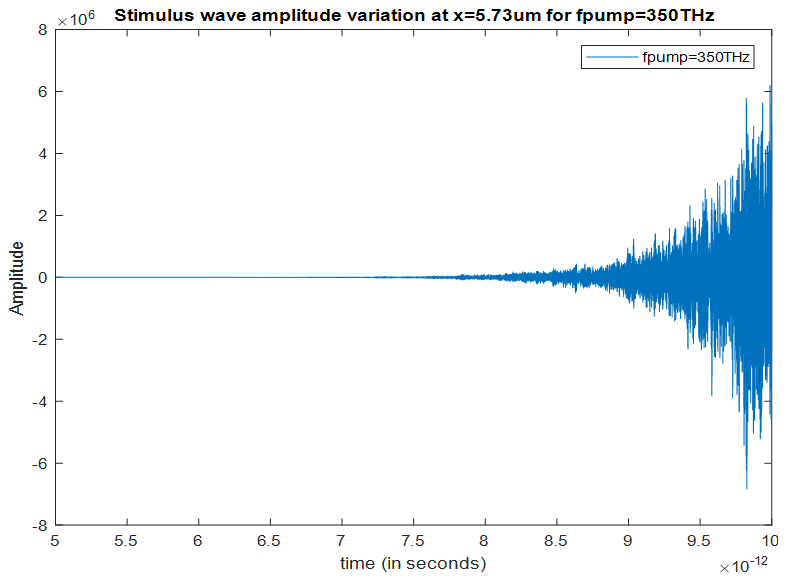 | Figure 16. Stimulus wave amplitude variation at x=5.73µm for a pump wave frequency of 350THz |
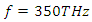 maximizes the intra-cavity energy and amplifies the stimulus wave, we choose this frequency as the frequency of pump wave excitation in order to compute the amplification (gain) spectrum of the stimulus wave. However, as already mentioned, the amplified stimulus wave is not monochromatic anymore due to the spectral broadening inside the cavity. Therefore, we must make a seperate analysis to obtain the gain spectrum of the stimulus wave, under a 350THz pump wave excitation.
maximizes the intra-cavity energy and amplifies the stimulus wave, we choose this frequency as the frequency of pump wave excitation in order to compute the amplification (gain) spectrum of the stimulus wave. However, as already mentioned, the amplified stimulus wave is not monochromatic anymore due to the spectral broadening inside the cavity. Therefore, we must make a seperate analysis to obtain the gain spectrum of the stimulus wave, under a 350THz pump wave excitation. 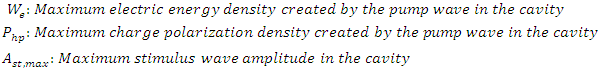 Part 2: Investigating the gain spectrum of the stimulus wave for a pump wave frequency of 350THz
Part 2: Investigating the gain spectrum of the stimulus wave for a pump wave frequency of 350THz | Figure 17. The configuration for computing the gain spectrum of the stimulus wave for 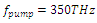 |
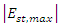 in the cavity for each stimulus wave frequency
in the cavity for each stimulus wave frequency 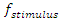 , in the range
, in the range 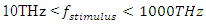 (THz to UV), for
(THz to UV), for 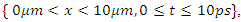 such that
such that 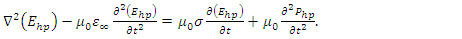 | (7a) |
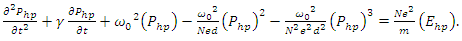 | (7b) |
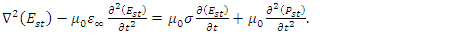 | (9a) |
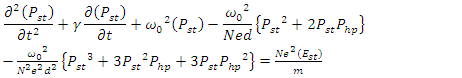 | (9b) |
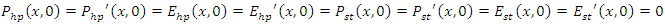 Boundary and excitation conditions:
Boundary and excitation conditions: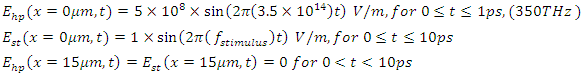 Absorbing boundary condition (perfectly matched layer):
Absorbing boundary condition (perfectly matched layer):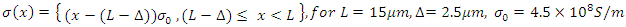 Optical isolator condition: Full reflection at
Optical isolator condition: Full reflection at 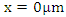
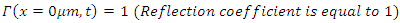 Switch controlled optical bandpass filter condition: Full reflection at
Switch controlled optical bandpass filter condition: Full reflection at 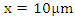 for
for 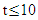 picoseconds, frequency dependent reflection at
picoseconds, frequency dependent reflection at 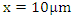 after t=10 picoseconds. For a given stimulus wave frequency (f), the magnitude frequency response of the filter is chosen to be
after t=10 picoseconds. For a given stimulus wave frequency (f), the magnitude frequency response of the filter is chosen to be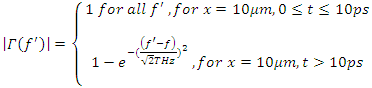 The amplification spectrum of the stimulus wave for
The amplification spectrum of the stimulus wave for 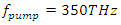 is tabulated below in Table 4. The stimulus wave is supplied to the cavity at t=0 as a quasi-monochromatic wave. For a given initial (at t=0) stimulus wave frequency, the center frequency of the band-pass filter is adjusted to be at the same frequency with the initial stimulus wave frequency. By doing so, we can observe how much gain can be obtained from the cavity for each stimulus wave frequency. We choose the pump wave frequency as
is tabulated below in Table 4. The stimulus wave is supplied to the cavity at t=0 as a quasi-monochromatic wave. For a given initial (at t=0) stimulus wave frequency, the center frequency of the band-pass filter is adjusted to be at the same frequency with the initial stimulus wave frequency. By doing so, we can observe how much gain can be obtained from the cavity for each stimulus wave frequency. We choose the pump wave frequency as 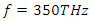 as it maximizes the amplification, and we sweep the stimulus wave frequency from 10THz to 1000THz in 10THz increments.
as it maximizes the amplification, and we sweep the stimulus wave frequency from 10THz to 1000THz in 10THz increments.
|
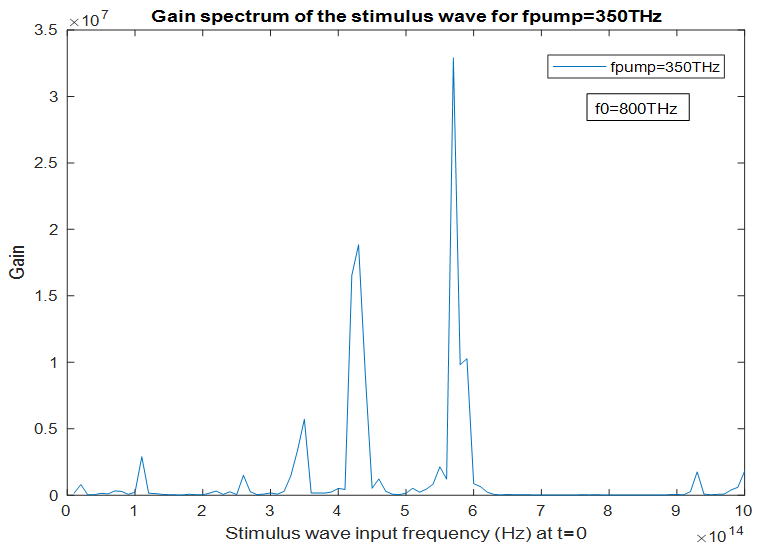 | Figure 18. Gain spectrum of the stimulus wave for 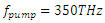 and and 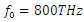 |
5. Conclusions
- In order to amplify a low power stimulus wave via nonlinear wave mixing in a low-loss optical microcavity, a high intracavity energy is required. As a summary for intracavity energy maximization and efficient wave amplification, the following requirements should be met: • The cavity should have a high quality (Q) factor.• For a given resonance frequency
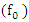 of the material, the high power pump wave frequency
of the material, the high power pump wave frequency 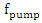 must be adjusted to maximize the electric energy density inside the cavity.Once these requirements are satisfied, it is possible to amplify a low power input wave, with a very large gain coefficient, by mixing it with an intense pump wave of very short duration, in a wide range of frequencies, inside a low-loss optical microcavity.
must be adjusted to maximize the electric energy density inside the cavity.Once these requirements are satisfied, it is possible to amplify a low power input wave, with a very large gain coefficient, by mixing it with an intense pump wave of very short duration, in a wide range of frequencies, inside a low-loss optical microcavity. 6. Appendix
6.1. Validation of the Computational Model and Results
- In this section, we will compare our finite difference time domain based computational model with the theoretical formula in the well-established context of sum frequency generation via nonlinear wave mixing, in the following example.Example: Nonlinear sum frequency generation (frequency upconversion)This example is about the generation of a higher frequency component
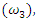 by mixing of two monochromatic waves with frequencies
by mixing of two monochromatic waves with frequencies 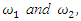 such that
such that 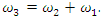 In order to achieve this, at least one of the waves must have a high intensity, so that nonlinearity arises, and wave mixing occurs.The high amplitude pump wave
In order to achieve this, at least one of the waves must have a high intensity, so that nonlinearity arises, and wave mixing occurs.The high amplitude pump wave  is generated at
is generated at 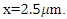 It has an amplitude of
It has an amplitude of 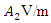 and a frequency of 180THz.
and a frequency of 180THz. 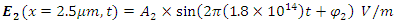 The input wave
The input wave 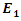 is generated at
is generated at 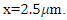 It has an amplitude of
It has an amplitude of 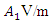 and a frequency of 120THz.
and a frequency of 120THz.
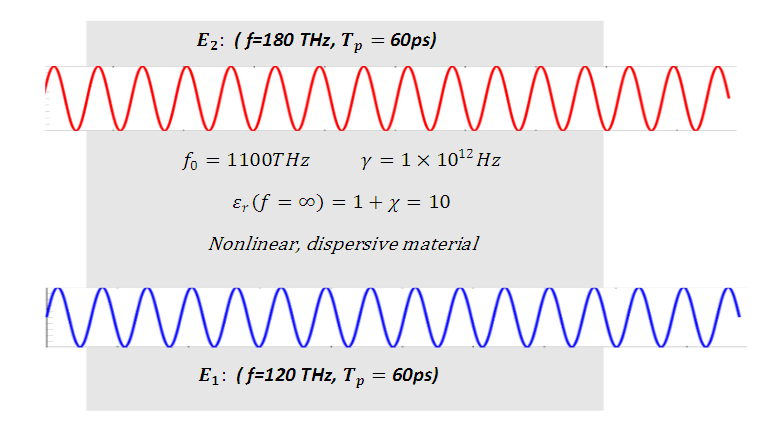 | Figure 19. Configuration for frequency upconversion |
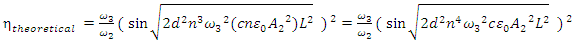 | (7) |
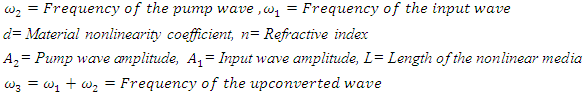 Our computational model is based on the finite difference time domain discretization of the nonlinear electron motion equation that involves the resonance frequency and the damping coefficient of the interaction medium. Coupled with the wave equation, the total wave
Our computational model is based on the finite difference time domain discretization of the nonlinear electron motion equation that involves the resonance frequency and the damping coefficient of the interaction medium. Coupled with the wave equation, the total wave 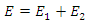 can be evaluated from:
can be evaluated from: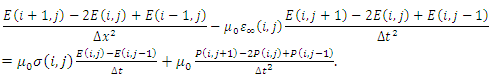 | (8a) |
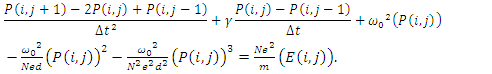 | (8b) |
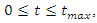 the computational formula for frequency upconversion efficiency is
the computational formula for frequency upconversion efficiency is 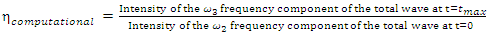 | (9) |
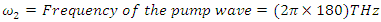
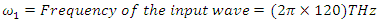
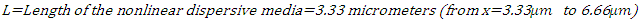
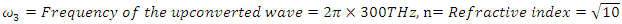 d= Material nonlinearity coefficient =
d= Material nonlinearity coefficient = 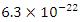 (The theoretical and the computational results agree for this value of d for a sample pump wave amplitude of
(The theoretical and the computational results agree for this value of d for a sample pump wave amplitude of 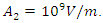 Our aim is to see if the results also agree for all the other pump wave amplitudes for this value of d)
Our aim is to see if the results also agree for all the other pump wave amplitudes for this value of d) 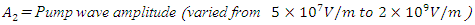
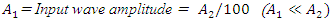
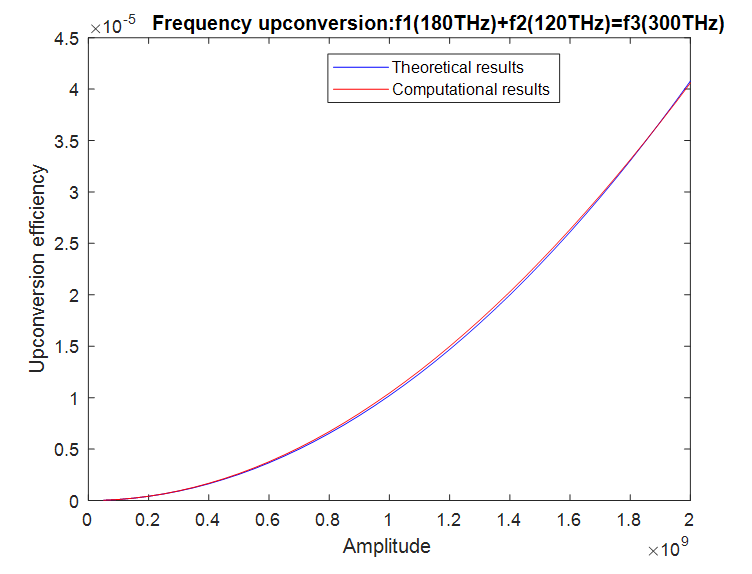 | Figure 20. Comparison of the frequency upconversion efficiencies for 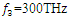 and and 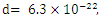 versus the pump wave amplitude versus the pump wave amplitude |
References
| [1] | Boyd Robert. W., Nonlinear Optics, Academic Press, New York, 2008. |
| [2] | Fox Mark, Optical properties of solids, Oxford University Press, New York, 2002. |
| [3] | Balanis Constantine. A., Advanced Engineering Electromagnetics, John Wiley & Sons, New York, 1989. |
| [4] | Bahaa E. A. Saleh, Malvin Carl Teich, Fundamentals of Photonics, Wiley-Interscience, New York, 2007. |
| [5] | Silfvast William. T., Laser Fundamentals, Cambridge University Press, New York, 2004. |
| [6] | Junkichi Satsuma, Nobuo Yajima, “Initial Value Problems of One-Dimensional Self-Modulation of Nonlinear Waves in Dispersive Media”, Progress of Theoretical Physics Supplement, Volume 55, January 1974. |
| [7] | Taflove Allen, Hagness Susan.C., Computational Electrodynamics: The Finite-Difference Time-Domain Method, Artech House, Boston, 2005. |
| [8] | Amit S. Nagra, Robert A. York, “FDTD Analysis of Wave Propagation in Nonlinear Absorbing and Gain Media”, IEEE TRANSACTIONS ON ANTENNAS AND PROPAGATION, VOL. 46, NO. 3, MARCH 1998. |
| [9] | Murray K. Reed, Michael K. Steiner-Shepard, Michael S. Armas, Daniel K. Negus, “Microjoule-energy ultrafast optical parametric amplifiers”, Journal of the Optical Society of America B, Volume 12, Issue 11, 1995. |
| [10] | Anna G. Ciriolo, Matteo Negro, Michele Devetta, Eugenio Cinquanta, Davide Faccialà, Aditya Pusala, Sandro De Silvestri, Salvatore Stagira, and Caterina Vozzi, “Optical Parametric Amplification Techniques for the Generation of High-Energy Few-Optical-Cycles IR Pulses for Strong Field Applications”, MDPI APPLIED SCIENCES, MARCH8 2017. |
| [11] | E. A. Migal, F. V. Potemkin, and V. M. Gordienko, “Highly efficient optical parametric amplifier tunable from near-to mid-IR for driving extreme nonlinear optics in solids”, Optics Letters, Vol. 42, Issue 24, pp. 5218-5221, 2017. |
| [12] | Chaohua Wu, Jingtao Fan, Gang Chen, and Suotang Jia, “Symmetry-breaking-induced dynamics in a nonlinear microresonator”, Opt. Express 27(20), 28133-28142 (2019). |
| [13] | Sung Bo Lee, Hyeon Sang Bark, and Tae-In Jeon, “Enhancement of THz resonance using a multilayer slab waveguide for a guided-mode resonance filter”, Opt. Express 27(20), 29357-29366 (2019). |
| [14] | Houssein El Dirani, Laurene Youssef, Camille Petit-Etienne, Sebastien Kerdiles, Philippe Grosse, Christelle Monat, Erwine Pargon, and Corrado Sciancalepore, “Ultralow-loss tightly confining Si3N4 waveguides and high-Q microresonators”, Opt. Express, Vol. 27, Issue 21, pp. 30726-30740 (2019). |
| [15] | Ivan S. Maksymov; Andrey A. Sukhorukov; Andrei V. Lavrinenko; Yuri S. Kivshar, “Comparative Study of FDTD-Adopted Numerical Algorithms for Kerr Nonlinearities”, IEEE Antennas and Wireless Propagation Letters, Year: 2011 | Volume: 10 | Journal Article | Publisher: IEEE. |
| [16] | E. Valentinuzzi, “Dispersive properties of Kerr-like nonlinear optical structures”, Journal of Lightwave Technology, Year: 1998 | Volume: 16, Issue: 1 | Journal Article | Publisher: IEEE. |
| [17] | Ozlem Ozgun, Mustafa Kuzuoglu, Metamaterials and Numerical Models, Nova Novinka; UK ed. Edition, 2011. |
| [18] | Ozlem Ozgun, Mustafa Kuzuoglu, MATLAB-based Finite Element Programming in Electromagnetic Modeling, CRC Press, 1st edition, 2018. |
| [19] | Mohammad Amin Izadi, Rahman Nouroozi, “Adjustable Propagation Length Enhancement of the Surface Plasmon Polariton Wave via Phase Sensitive Optical Parametric Amplification”, Scientific Reports volume 8, Article number: 15495 (2018). |
| [20] | Ozlem Ozgun, Mustafa Kuzuoglu, “Non-Maxwellian Locally-Conformal PML Absorbers for Finite Element Mesh Truncation”, IEEE Transactions on Antennas and Propagation 55(3): 931 - 937 • April 2007. |
| [21] | Ozlem Ozgun, Mustafa Kuzuoglu, “Near-field performance analysis of locally-conformal perfectly matched absorbers via Monte Carlo simulations”, Journal of Computational Physics, Volume 227 Issue 2, December, 2007, Pages 1225-1245. |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML
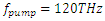 and
and 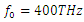
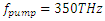 and
and