1. Introduction

The electroencephalogram (EEG) signals shows brain activities. So that brain disorders can be detected by the study of EEG signals [1-3]. But Processing large amount of data is laborious and it increases error in the system. To improve it, automatic diagnosis methods have been noticed for EEG signals [4-7]. The demand for more accurate automatic mental detection increases the need for growing computational methods recently.

Automatic disorders detection in EEG signals consists mainly of two steps. The first step is feature extraction and the second step is classification. Fourier transform (FT), wavelet transform (WT) as two famous methods in signal processing which are usually used for feature extraction in EEG signals [8, 9].

FT is the most famous method in signal processing which is proper for analyzing stationary signals. However, non-stationary signals cannot be detected by FT. To cope with this issue, short time fourier transform (STFT) is used to non-stationary signals by assuming a fixed window to concentrate on certain period of time [8]. Although it can be used for simple time varying signals but it has some difficulties in non-stationary signals with high degree of nonlinearity or uncertainty [10]. This is due to the limitation of the fixed window.

Wavelet transform (WT) is recently used in EEG for analyzing signals [9, 11]. It does not need to get a fixed window, it provides a short window for high frequency components and long window for low frequency components [12], so it can be used for time varying signals. WT is able to consider the time and the frequency information together; therefore, it can be known as a time-frequency representation of the signal [13].

After features of signals are extracted, different methods are used for classification and diagnosing the disorders. There are two main classification methods in the literature of EEG analysis, parametric and non-parametric methods. Parametric methods like mean, variance,… are used when statistical distributions of faults are accessible [14]. Unfortunately, they are not available in the most cases. On the other hand, non-parametric methods do not need statistical characteristic of the signal.

For example, they can be obtained by a description of the signals, like, fuzzy logic (FL) [8], or data driven methods, such as, artificial neural network (ANN) [9, 14-16].

Intelligent methods are proved to be powerful in many applications in different fields like estimation [17, 18], classification [9, 14, 15]. ANN as a famous intelligent method can effectively capture characteristics of signals, learn from data, and give a proper response for new data input. These properties make ANN more suitable when a group of data is available for training the network.

This paper presents a new method for detecting seizure and epilepsy. For this propose, it is assumed that EEG signals of healthy people and seizure and epilepsy patients are available. First, wavelet transform (WT) is applied on EEG signals to decompose signals at different levels. Then, the energies of signals at different levels are calculated to build their feature vectors. Then, an ANN as a powerful intelligent tool is used to classify the EEG signals. Radial basis function (RBF) is considered. The novelty of the purposed method is in the way it is designed. For the first, the energies of different levels of signals are applied to obtain a unique feature vector. RBF as a famous network is shown to be a strong classifier in this field. The designed system can diagnose different diseases correctly. Finally, the proposed classifier method robust against noise. Through a simulation study, real data of EEG signals are used. Simulation results show the ability of the proposed method in diagnosing disorders.

The paper is organized as follows. Section 2 describes different types of EEG signals. Section 3 briefly demonstrates the basic theory of the methods used in this paper. Design methodology and simulation study are considered in Section 4. Simulation results are illustrated in Section 5. Finally, concluding remarks are given in Section 6.

2. Data Descriptions

Data described in [19] has been used which is publicly available. In this section, only a short description is given and it is referred to [19] for further details. The complete dataset consists of five sets (denoted A–E), each containing 100 single-channel EEG signals of 23.6 s. Each signal has been selected after visual inspection for artifacts and has passed a weak stationary criterion. Sets A and B have been taken from surface EEG recordings of five healthy volunteers with eyes open and closed, respectively. Signals in two sets have been measured in seizure-free intervals from five patients in the epileptogenic zone (D) and from the hippocampal formation of the opposite hemisphere of the brain (C). Set E contains seizure activity, selected from all recording sites exhibiting ictal activity. Sets A and B have been recorded extracranially, whereas sets C, D, and E have been recorded intracranially.

3. The Basic Theory of the Suggested Methods

In this section, first, the basic theory of discrete wavelet transform is illustrated. Then, some concepts on artificial neural network are considered.

3.1. Discrete Wavelet Transform (DWT)

Discrete wavelet transform (DWT) presents a signal as a combination of scaling functions and their wavelets at different locations (positions) and scales (duration). DWT is introduced to map a discrete signal into different resolution levels [20].

In [21] introduces a unique framework for discrete wavelet, known as multi-resolution analysis (MRA). The aim is to decompose signal 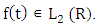For this purpose, consider 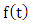as a linear combinations of scaling functions and its orthogonal wavelets as follows:

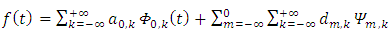(1)

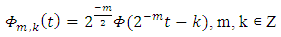(2)

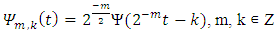(3)

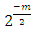Where φ(t) and ψ(t) are scaling functions and their orthogonal wavelets, and m and, k are dilation and translation factors of the scaling functions and the wavelets, respectively. It has to be noticed that is used as an energy normalization factor. 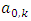and 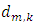can be computed as the following:

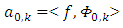(4)

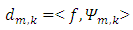(5)

Figure 1 shows the decomposition of a signal based on MRA.

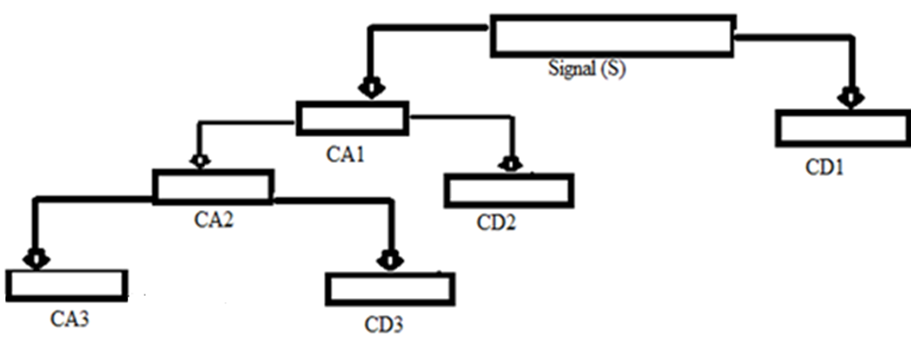Figure 1. The decomposition of a signal based on MRA

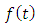The energy of the signal based on Parseval's theorem can be obtained as follows:

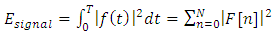(6)

Where T and N are time period and length of the signal, respectively.

3.2. Artificial Neural Network (ANN)

Ability of artificial neural networks (ANNs) to learn complex nonlinear functions motivates their applications in different fields. They aim to mimic biological nervous systems using massive interconnection of individual processing elements called neurons in a multi-layered architecture. The layered topology of neurons provides great promise to compactly emulate a very general nonlinear function.

Therefore, multi layered perceptron (MLP) represents the most popular class of neural networks, consisting of multiple layers of artificial neurons in a feed forward. It potentially provides a generic model representation for nonlinear black box systems which can be adapted with experimental input output data [18, 22]. Although Feed forward neural networks, trained with the back propagation (BP) algorithm, have been widely used in different fields [18, 23, 24]. However, there are faced with several drawbacks such as potentially pre converging to a local minima, relatively slow convergence rate, and difficulties to determine an adequate architecture to obtain a minimum [18, 23, 24].

Radial basis function (RBF) neural networks has a universal approximation ability. The work reported in this paper uses RBF neural network due to its structural simplicity and general approximation capabilities. A RBF neural network has an input layer, a nonlinear hidden layer and a linear output layer. The nodes within each layer are fully connected to the previous layer nodes. The output layer nodes are weighted linear combinations of the RBF in hidden layer. The structure of a RBF neural networks with m inputs, p outputs and N hidden nodes is depicted in Figure 2.

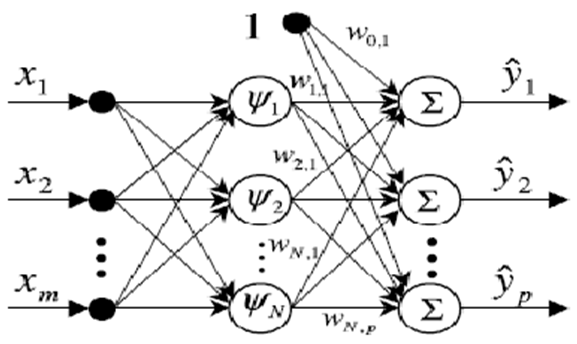Figure 2. RBF neural networks structure

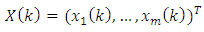Where and 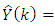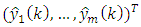denote input and output vectors, respectively. 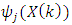is a nonlinear function which is chosen as a Gaussian activation function:

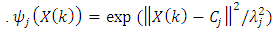(7)

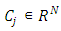Where indicates the center of the jth hidden unit, 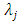is the width of the jth RBF hidden unit.

Then, the ith RBF network output can be represented as a linearly weighted sum of N basis functions as follows:

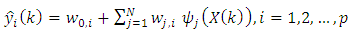(8)

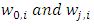where represent the weights [18 & 25-26].

4. Design Methodology and Simulation Study for the Purposed System

In this section, first, wavelet transforms of EEG signals introduced in Section 2 are analyzed and proper features are selected. Then, a RBF network is tuned to classify the purposed faults.

4.1. Feature Extraction with Wavelet Transform

Feature extraction is an important task in pattern reorganization, classification, machine learning and data mining. Feature extraction is used to find the common properties among a group of signals. This has a high effect on the accuracy of classifiers. On the other hand, wavelet transform is a powerful method for analyzing non-stationary signals, because of this; it is used in EEG signals [9, 11].

This section presents the suggested feature extraction method based on wavelet transform. For this purpose, the patient signals are decomposed by MRA method to obtain decomposition levels known as details. To have a successful feature extraction and consequently classify different types of signals, it is important to choose level of decomposition and type of wavelet properly. For this reason, decomposition of EEG signal type E is made by different types of wavelet to evaluate which wavelet is more efficient for the suggested design methodology. The level of decomposition is chosen to be 3. Figure 3 and 4 show the type E signal and its decomposition levels for Haar and Daubechies 3 (db3) mother wavelets.

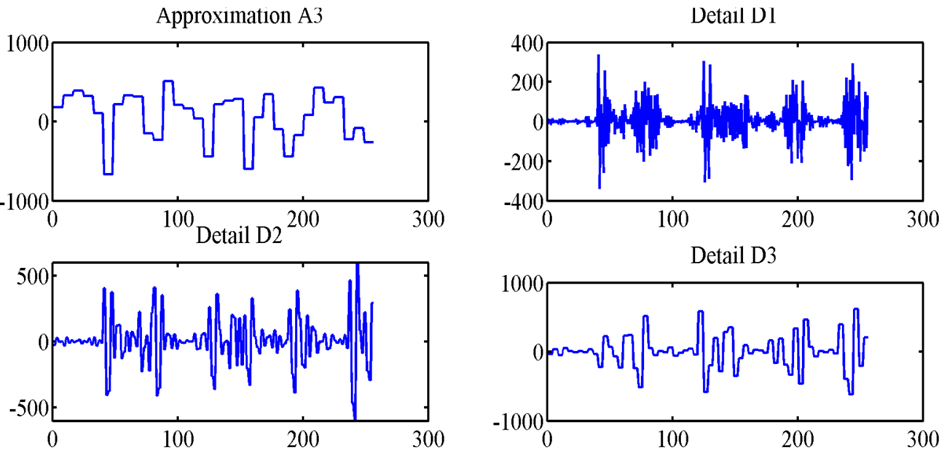Figure 3. Type E signal and its decomposition levels for Haar wavelets

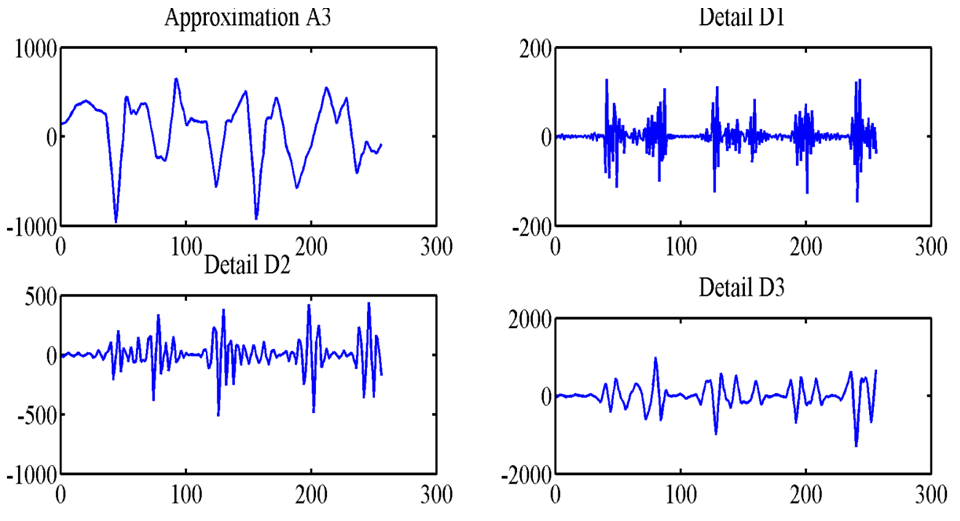Figure 4. Type E signal and its decomposition levels for db3 wavelets

The vertical axis is magnitude of the signal and the horizontal axis is the sampling time. To have a proper feature extraction, db3 is chosen to be the mother wavelet. Figure 5 and 6 show type D and C signals and their decomposition levels with db3 wavelets.

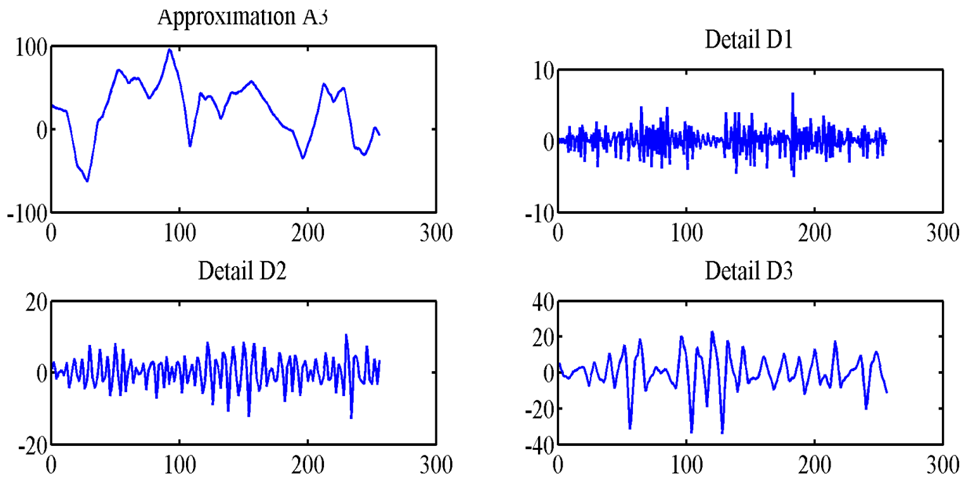Figure 5. Type D signal and its decomposition levels for db3 wavelets

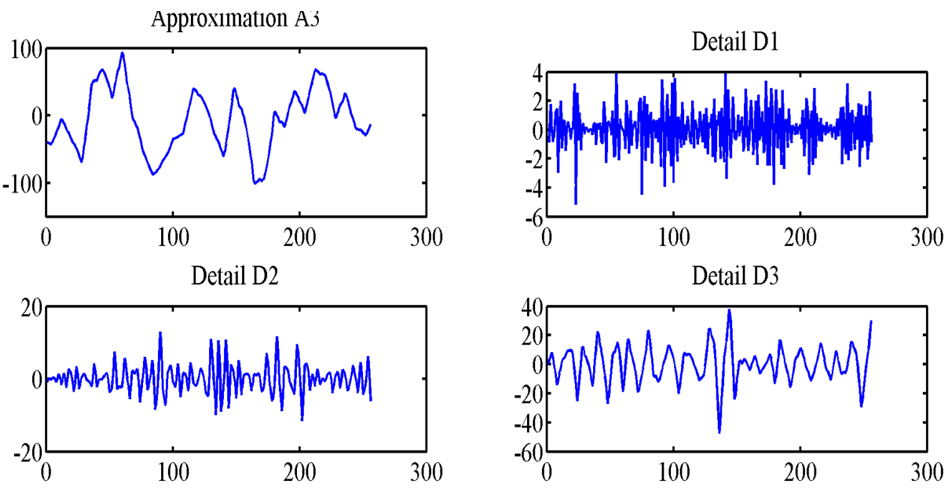Figure 6. Type C signal and its decomposition levels for db3 wavelets

In this paper, the energies of decomposition levels D1, D2, D3 and A3 are computed by Eq. (6) and they are used for feature extraction.

Now a new vector is taken as feature in the following:

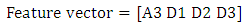(9)

4.2. Classification with RBF Network

This subsection presents the structure of the suggested RBF network for classification of EEG signals.

The aim is to design a RBF network to receive the feature vector in Eq. (9) and classify the unhealthy signals correctly. For this purpose, a three layered RBF network with four inputs, fifty five neurons in the hidden layer and one output is design. The neural network is trained with the feature data as input and decision vector as output using back-propagation (BP) algorithm. Gaussian and linear functions are used in the hidden and output layers, respectively.

5 different data sets are used for training the suggested RBF network. Different output level ranges are considered in the RBF to indicate different healthy and unhealthy cases. For this purpose, output levels in the ranges of 0.5 to 1.5, 1.5 to 2.5, 2.5 to 3.5, 3.5 to 4.5 and 4.5 to 5.5, are allocated to the types 1, 2, 3, 4 and 5, respectively.

5. Simulation Tests and Results

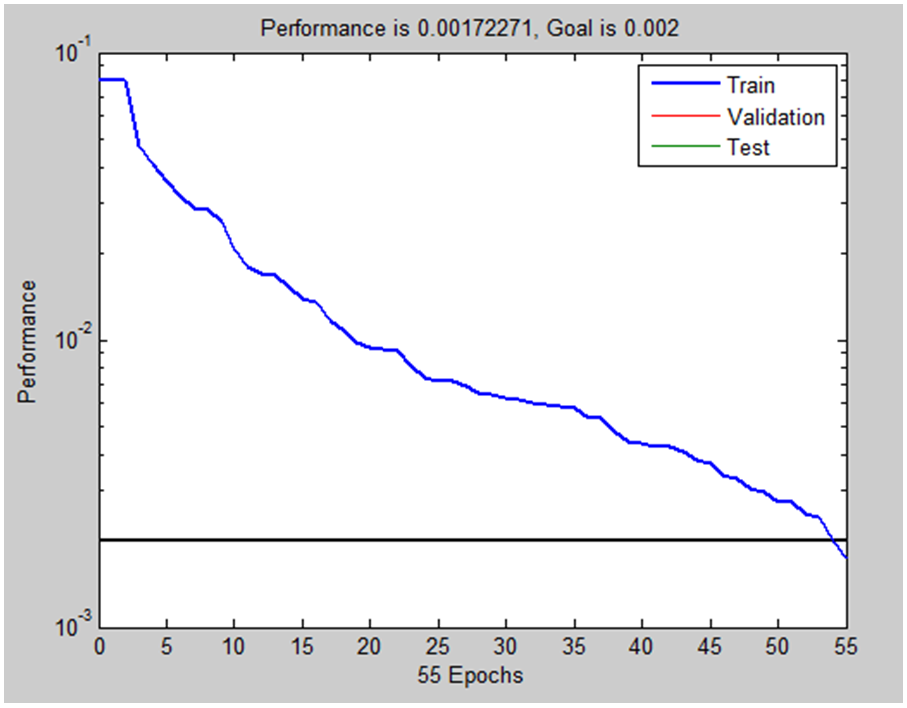
In this section, different data of EEG signals are considered to evaluate the designed system. For this purpose, after features are extracted from different types of signals, they are applied to the RBF network to classify the data. Figure 7 show the performance of the RBF network.

Figure 7. The performance of the RBF system

Figure 8 shows the output of the classifier. It can be seen from Figure 8 that the designed system can classify different types of the EEG signals correctly. The mean squared error (MSE).

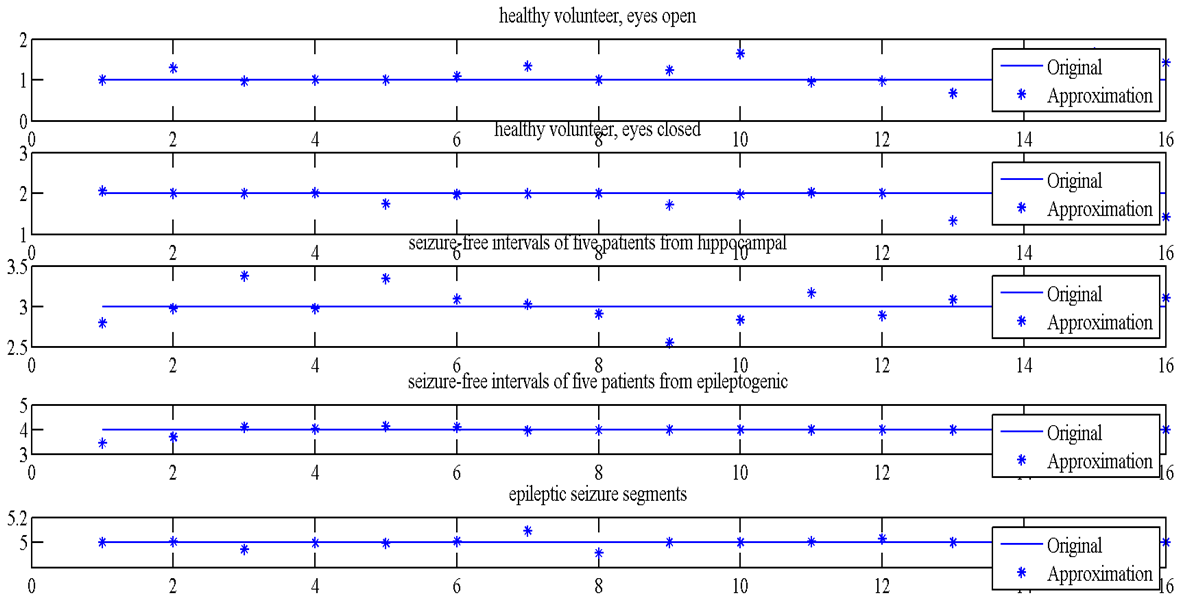Figure 8. The output of the classifier

The mean squared error (MSE) of EEG signals is illustrated in Table 1.

Table 1. The MSE error of the EEG signals

The best performance is belonged to EEG signal type E which stands at 0.0013. Regarding EEG signals type C and D, the MSE are 0.0380 and 0.0282, respectively, which is acceptable.

6. Conclusions

This paper presented a new classification system for EEG signals using feature extraction and intelligent method. For this purpose, first, different types of EEG signals were introduced. Then, wavelet transform was applied for feature extraction of the mentions signals. Different mother wavelets were considered to see which one is the best for this application. The db3 proofs to be suitable. Then, using decomposition levels of the signals, their energies were computed. For the first time, the energies of different levels of signals are considered for feature extraction which show to be a powerful tools. RBF network is also used in classification section. BP algorithm is applied to train the system. RBF network has a faster train algorithm camper to MLP network and a better convergence as it does not have local minimum problem. These energies are fed to the inputs of the RBF network to classify the signals. The suggested system could successfully diagnosis types of disorder. Simulation test showed the ability of the designed system on the data of EEG signals.

ACKNOWLEDGMENTS

The authors would like to thank Professor Andrzejak for using his EEG data.

Nomenclature