-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Electromagnetics and Applications
p-ISSN: 2168-5037 e-ISSN: 2168-5045
2015; 5(1): 8-12
doi:10.5923/j.ijea.20150501.02
Determination of the Propagation Constant along a Thin Vertical Wire on the Earth's Surface
Ghada M. Sami 1, 2, Mnerh N. Al-qahtani 3
1Mathematics Department, Faculty of Science, Ain shams University, Cairo, Egypt
2Mathematicsand Statistics Department, Faculty of Science, King Faisal University, KSA
3Mathematicsand Statistics Department, Faculty of Science and Arts, Damam University, KS
Correspondence to: Ghada M. Sami , Mathematics Department, Faculty of Science, Ain shams University, Cairo, Egypt.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
In this paper, we will perform theoretical and numerical analysis of the propagation constant along a thin vertical wireon the earth’s surface. It is very fundamental problem in electromagnetic theory. The wire is assumed to be placed vertical to the earth’s surface in a stratified homogeneous medium, which is represented by a finite set of horizontal plane layers characterized by conductivities. The electromagnetic properties of a current along a thin vertical wireon the earth’s surface will be reviewed and a solution will be given for the boundary value problem of a wave propagating. In this paper a general modalequation is derived for the propagation constant of the transmission current on the wire. In addition, numerical results are represented graphically.
Keywords: Electromagnetic field, Layered media, Wave propagation
Cite this paper: Ghada M. Sami , Mnerh N. Al-qahtani , Determination of the Propagation Constant along a Thin Vertical Wire on the Earth's Surface, International Journal of Electromagnetics and Applications, Vol. 5 No. 1, 2015, pp. 8-12. doi: 10.5923/j.ijea.20150501.02.
Article Outline
1. Introduction
- The study of wave propagation in the earth has a history that extends back to the beginning of the last century and is an interesting topic. Most of the investigations are based on the rigorous theoretical solutions of Sommerfeld [1] and Weyl [2] for a vertical antenna over a flat homogeneous semi-infinite conducting earth. Practical formulas, valid at large distances from the antenna, are based on the use of asymptotic expansions.All treatments of the phenomenon of the wave propagation took the earth surface as a perfectly smooth (planar or spherical) interface between the air and ground or water. Feinberg [3] published a result derived from an integral equation that dealt with the problem of radiation above a planar earth with terrain irregularities. He showed that the effect of small height irregularities would decrease the apparent conductivity of the earth. Details of his derivation were not published, and his result did not show the effect of that finite earth conductivity; the term accounting for roughness was obtained as though the surface is perfectly conducting. Bremmer [4] repeated Feinberg’s result.Natural propagation can be helpful to solve some specific problems, such as radio communications in mines with rooms and pillars which cannot be solved easily with the help of transmission lines. Natural propagation modes are also useful for short range communications, for example, in some road tunnels. Recently, Zheng [5] studied the wave propagation theories and application. The case in which the wire is parallel to the plane interface between two homogeneous half-spaces is of particular interest in a number of technical and physical applications. Early attempts Carson [6] and Wise [7] to solve the problem were based on transmission line analogies that led to useful results, particularly at the low frequency end of the spectrum. Similar developments are found in Sunde [8] excellent text on earth conduction effects in power-line systems. More recent works have dealt with the high frequency behavior (kikuchi [9]). The first use of full wave theory for a wire above a two - layer medium was presented by Kuester and Chang [10].Many efforts to develop models for the stratified earth structure are reported in the literature. They are mainly focused on the calculation of the earth return impedances and each of them uses different concepts and approximations. Nakagawa’s multilayered earth model (Nakagawa [11]) can be assumed as the most generalized, since it allows different electromagnetic properties for each earth layer. However, the accuracy of these models is limited to the low frequency range, especially for cases of high earth resistivity, since they all neglect the influence of the imperfect earth on the shunt admittances. Furthermore, Ametani [12] proposed formulas for the shunt admittances in the case of a two-layer earth. Wait [13], computed the propagation constant for a straight wire of infinite length located in a stratified media, and studied the electromagnetic waves in stratified media.Also, Mahmoud and Wait [14] studied that wave propagation along a thin wire located inside a rectangular waveguide with imperfectly reflecting boundaries. Coleman [15] studied the wave propagation for the case of a thin wire on the interface between two semi-infinite homogeneous media. Recently, Robert [16] studied the electromagnetic wave propagation on a thin wire above earth. Yingkang et .at. [17] obtained the wave propagation along a thin vertical wire antenna placed in a horizontally layered media and Manjunath et. at. [18] studied the wave propagation in random granular chairs.In this paper, we assume that the current on the wire, for a localized generator, it can be constructed by a linear superposition of exponential current modes. In addition, a solution will be given for the boundary value problem of a wave propagating along a thin vertical wireon the earth’s surface. To solve the boundary value problem, we let that the wire carries a current of the form
 and
and  is the propagation constant that is to be determined in terms of the series impedance and series admittance of the wire Lavrov and Knyazev [19]. We deduce a modal equation for the propagation constant along the wire which is in a suitable form to yield numerical results.The aim of this paper is to perform the theoretical and numerical analysis of the propagation constant along a thin vertical wireon the earth’s surface by using the modal equation for the propagation constant. The modal equation will be used for the propagation constant to obtain the wave propagation along a thin vertical wireon the earth’s surface. In addition, we will use the available numerical methods to obtain the results of some of the important special cases for the modal equation.
is the propagation constant that is to be determined in terms of the series impedance and series admittance of the wire Lavrov and Knyazev [19]. We deduce a modal equation for the propagation constant along the wire which is in a suitable form to yield numerical results.The aim of this paper is to perform the theoretical and numerical analysis of the propagation constant along a thin vertical wireon the earth’s surface by using the modal equation for the propagation constant. The modal equation will be used for the propagation constant to obtain the wave propagation along a thin vertical wireon the earth’s surface. In addition, we will use the available numerical methods to obtain the results of some of the important special cases for the modal equation.2. Mathematical Formulation of the Problem
- We consider the problem shown in Figure (1) for a long thin wire of radius a. We assume that the wire very thin compared to its length. In medium 1, the permittivity and permeability of free-space are
 and
and  , respectively.
, respectively. | Figure (1). Geometry for the infinite wire at y = h over the interface at x = 0 |
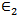 ,
,  , respectively. We chosen a Cartesian coordinate system (x, y, z) and oriented along the positive z-axis and located at y = h and x = 0.Thus, for the solution of the boundary value problem, we let the current have the form
, respectively. We chosen a Cartesian coordinate system (x, y, z) and oriented along the positive z-axis and located at y = h and x = 0.Thus, for the solution of the boundary value problem, we let the current have the form 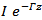 , where
, where  is the propagation constant.
is the propagation constant.3. The Method of the Solution and Modal Equation
- It is convenient in the present problem to express the total electromagnetic field in terms of two scalar potentials. The components
 and
and 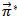 are the electric and magnetic Hertz vectors respectively.For the region
are the electric and magnetic Hertz vectors respectively.For the region  , (in medium 1),
, (in medium 1), | (1) |
 | (2) |
 | (3) |
 | (4) |
 | (5) |
 | (6) |
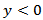 , (in medium 2) same equations hold, but we add a subscript two to all relevant quantities. The boundary conditions require at y = 0 that
, (in medium 2) same equations hold, but we add a subscript two to all relevant quantities. The boundary conditions require at y = 0 that 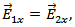
 We get that the primary fields of the infinite wire can be derived from the potential
We get that the primary fields of the infinite wire can be derived from the potential 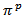 given by Wait [20]
given by Wait [20] | (7) |
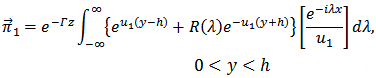 | (8) |
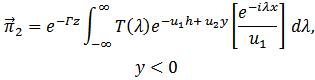 | (9) |
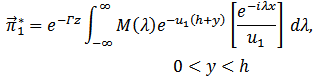 | (10) |
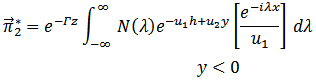 | (11) |
 ,
,  The wave numbers
The wave numbers  and
and  for the two media, are
for the two media, are In the equations (8)-(11), we have omitted the factor
In the equations (8)-(11), we have omitted the factor  on the right-hand sides, the boundary conditions can be applied to obtain the unknown functions
on the right-hand sides, the boundary conditions can be applied to obtain the unknown functions  , then we have
, then we have | (12) |
 | (13) |
 | (14) |
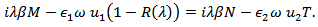 | (15) |
 as
as | (16) |
 In the case of
In the case of 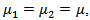 , equation (16) leads to
, equation (16) leads to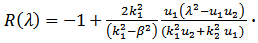 | (17) |
 in the upper half – space due to the current
in the upper half – space due to the current  is
is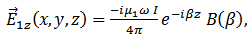 | (18) |
 | (19) |
 hence, we can write the component
hence, we can write the component 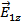 as
as | (20) |
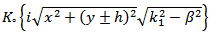 is the modified Bessel function of the second kind.The boundary conditions at the assumed perfectly conducting wire, we must have
is the modified Bessel function of the second kind.The boundary conditions at the assumed perfectly conducting wire, we must have  . Subject to the thin wire approximation, we can choose matching point in arbitrary fashion. For convenience, we are substituting in equation (19) for y = h and x = a, hence,
. Subject to the thin wire approximation, we can choose matching point in arbitrary fashion. For convenience, we are substituting in equation (19) for y = h and x = a, hence, | (21) |
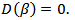 | (22) |
4. Some Special Cases and Modal Equation
- First case, when the lower conducting half - space is perfectly conducting, the imaginary part of the wave propagation constant is equal to wave number
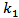 . If we are substituting the values
. If we are substituting the values  in equation (21), we see that simply
in equation (21), we see that simply  that corresponds to propagation in the form of TEM mode on transmission line over perfect ground plane.Second case, the rather fundamental nature of this limiting case, for
that corresponds to propagation in the form of TEM mode on transmission line over perfect ground plane.Second case, the rather fundamental nature of this limiting case, for  , then from equation (21) we can write
, then from equation (21) we can write  | (23) |
 located vertical on the interface, a valid solution for
located vertical on the interface, a valid solution for  is determined from the property of the integrand in equation (23) as
is determined from the property of the integrand in equation (23) as 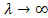 .Noting that,
.Noting that,  | (24) |
 and
and  in the denominator, we get
in the denominator, we get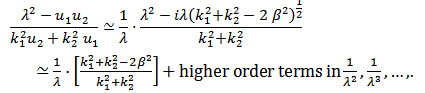 | (25) |
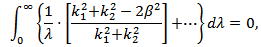 then, we have
then, we have hence,
hence, | (26) |
 located vertically on the interface for non-magnetic media of the two wave numbers
located vertically on the interface for non-magnetic media of the two wave numbers 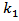 and
and  , is
, is | (27) |
5. Numerical Results
- A theoretical and numerical analysis of the wave propagation along a thin vertical wire on the earth's surface have been studied. The wire assumed to be placed vertically on the earth's surface, and the current distribution along a thin vertical wire is obtained in terms of the propagation constant.In this paper, we studied two special cases for the modal equation to obtain the propagation constant to get the current in the wire. Numerical results presented and plotted to show the relation between the current in the wire and the direction of the propagation on the wire for different values of frequencies. The direction of the propagation is z-direction.The imaginary part of the current along a thin vertical wire on the earth's surface have been plotted in Figure (2) and Figure (3), by using the two special cases for the modal equation. Figure (2) and Figure (3) show that, the imaginary part of the current along a thin vertical wire on the earth's surface, for different values of frequencies f = 50 MHz, 130 MHz, and 200 MHz, at the rate of variation of the phase of the wave along z-direction
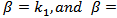
 respectively.These Figures show that with the increasing direction of the propagation on the wire and increasing in the frequency, the current along thin vertical wire on the earth's surface decrease. Also, we conclude that the increases current along the wire depend on the rate of variation of the phase of the wave along z-direction, which depend on the two wave numbers
respectively.These Figures show that with the increasing direction of the propagation on the wire and increasing in the frequency, the current along thin vertical wire on the earth's surface decrease. Also, we conclude that the increases current along the wire depend on the rate of variation of the phase of the wave along z-direction, which depend on the two wave numbers  and
and  .
.6. Conclusions
- Wave propagation is the process of communication involves the transmission of information from one location to another. Modulation is used to encode the information onto a carrier wave, and may involve analog or digital methods. It is only the characteristic of the carrier wave which determines how the signal will propagate over any significant distance. The wave propagation along a thin vertical wire on the earth's surface by using modal equation, can be performed. The modal equation for the propagation constant along a thin vertical wire on the earth's surface is derived. We studied some of the important special cases for the modal equation that enable us to get the propagation constant. The direction of the propagation is in a z-direction, then the waves has only z-component of the electric field. We conclude that the propagation constant depend on the choice of the matching point on the wire. The imaginary part of the current depend on the rate of variation of the phase of the wave
 along z direction represented graphically.Some of the important special cases are recovered and are seen to agree with the previous work [17].
along z direction represented graphically.Some of the important special cases are recovered and are seen to agree with the previous work [17]. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML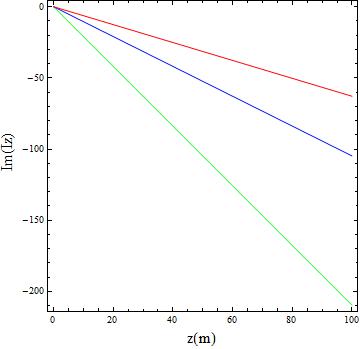
 . The red, blue, and green curves corresponding to the different values of frequencies, f = 50 MHz, 130 MHz, and 200 MHz, respectively
. The red, blue, and green curves corresponding to the different values of frequencies, f = 50 MHz, 130 MHz, and 200 MHz, respectively
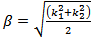 . The red, blue, and green curves corresponding to the different values of frequencies,f=50MHz, 130MHz, and 200 MHz, respectively
. The red, blue, and green curves corresponding to the different values of frequencies,f=50MHz, 130MHz, and 200 MHz, respectively