1. Introduction

Developing an equivalent circuit model for an antenna has both theoretical interest and practical importance. If the suggested equivalent circuit is closely related to the physical parameters and geometry of the antenna, it can offer useful insights into the performance and design of the antenna. In the design of radio-frequency transceivers, the equivalent circuit model of the antenna enables the simulation of the entire transceiver system in the time domain where nonlinear devices such as amplifiers and mixers are more easily characterized [1, 2].

Several equivalent circuit models have been proposed using the aspect of input impedance or admittance matching. For instance, Wang introduced degenerated Foster canonical forms for electric and magnetic antenna models [3]. Wang and Li circuit refinement method consists of a narrow band model augmented with a macro model [4]. Ansarizadeh circuit topology for rectangular microstrip patch antenna used a non-linear curve-fitting optimization technique to determine exact values for the parameters of the equivalent circuit model [5]. A. Ferchichi et al proposed two electrical models for carpet and gasket Sierpenski patch antennas [6]. Then they developed an electrical model to represent the input admittance of an antenna array with a finite number of elements [7]. Y. Kim and H. Ling presented a significantly improved method to construct an equivalent circuit for a broadband antenna [8]. The vector fitting was introduced for the robust rational function approximation of broadband antennas. The constrained Particle Swarm Optimization (PSO) was then proposed to optimize the sample locations to find the best passive rational function model. Antennas are also modeled by the resulting circuit parameters from the geometry of the antenna. For example, a lumped equivalent circuit model is applied to a small planar meander-line monopole antenna whose radiating element is backed by a metallic plate [9]. The lumped circuit model was also derived by separating the antenna structure into different stages of; feed-line, steps, and patch [10, 11].

Extensive studies have been reported in the early papers [12] on modeling dipole antenna using RLC lumped elements. They have high accuracy in modeling the input impedance of linear dipole antenna. A lumped circuit model was constructed for a dipole antenna by considering length and losses of the dipole as precise as possible, and the circuit parameters were determined by using an optimization theory of the genetic algorithm (GA) [13]. Some other models were also reported in the literature [14, 15].

This paper investigates modeling of dual-band monopole antennas. A crescent-shape planar monopole antenna designed for wireless local area network (WLAN) application [16] is considered in the investigations. The impedance and reflection coefficient at the strip line feeding reference port is obtained using CST Microwave Studio while the equivalent circuit is verified using MATLAB and ADS. The paper is organized as follows. Section 2 discusses approaches for representing the antenna by equivalent circuit models comprising several lumped elements. The foster canonical forms and the rational functions are investigated. Section 3 presents the results of simulations, where a crescent-shape planar monopole antenna designed for (WLAN) application is considered in the study case. The second investigated approach is the SPICE–compatible equivalent circuit modeling using vector fitting technique. The equivalent circuits are derived from either of input impedance, input admittance or reflection coefficient responses against frequency. The obtained conclusions are listed in section 4.

2. The Approaches to get Antenna Equivalent Circuits

The antenna can be represented by an equivalent circuit of several lumped elements. Two approaches are outlined in the following sections that model the antenna input impedance. The first approach is based on foster canonical forms. The second approach is an SPICE–compatible equivalent circuit using vector fitting technique. Both of these approaches aim mainly at describing the antenna frequency characteristics.

2.1. The Equivalent Circuit Based on Foster Canonical Forms

Generally, antennas are linear, passive elements whose input impedances can be represented by Foster canonical forms, as shown in Fig.1, which assumes no ohmic loss. The first Foster canonical form (Fig.1a) is suitable for modeling “electric antennas” which behave as an open circuit at DC input signal. The second Foster canonical form (Fig.1b) is for modeling “magnetic antennas” which are electrically short at DC input signal. For example, dipole and monopole antennas are electric antennas while loop antennas are magnetic antennas [3]. The input impedance Z_in(ω) of the antenna is modeled here by means of the equivalent network depicted in Fig.(1a) [17].

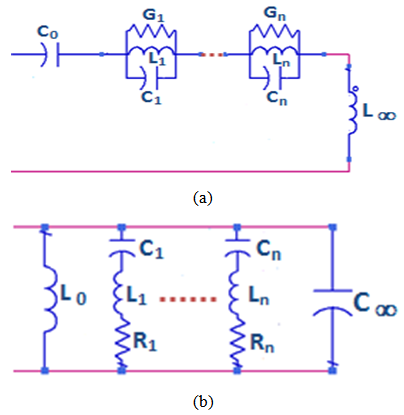Figure 1. Foster canonical forms of the equivalent circuit for (a) electric antennas and (b) magnetic antennas

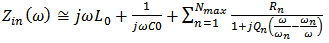(1)

Where Q_n=ω_nR_nC_n and ω_n=(L_nC_n)^-0.5. N_max is the number of modes needed to properly describe the frequency behavior of the antenna input impedance. ω is the operating radian frequency, and ω_n is the radian frequency of the n^th resonant mode. C₀ is the quasi-static input capacitance, and L₀ is an inductance that takes into account the higher order modes as well as for feeding effects, while C_n, L_n, R_n and Q_n are the capacitance, inductance, resistance, and quality factor, respectively, describing the lumped resonance processes that take place in the antenna structure [17].

2.2. An Analytical Method Using Rational Transfer Function

A rational transfer function is a form of transfer function in Laplace domain consisting of numerator polynomials and denominator polynomials, whose coefficients can be determined by fitting simulation result [18]. The overall performance of an antenna can be characterized by a rational transfer function which yields the feasibility to combine the antenna with other components in the communication system rather than an independent part as in conventional design [18]. The rational approximation of a transfer function F(s) can be written as [19]:

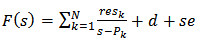(2)

Where s = jω represents the complex frequency, res_k and p_k denote the k^th residue and k^th pole, respectively, which may be either real quantities or complex conjugate pairs. The k^th residue is extracted by using a fitting procedure such as the Vector Fitting (VF) technique [19]. d is a constant term and e is the proportionality term. With the assumption that F(s) is an admittance–type function, the constant term d and the s–proportional one can be synthesized with a resistance and a capacitance whose values are 1/d and e respectively. The equivalent circuit for the remaining parts of F(s), res_k, and s-p_k can be characterized for the following two cases [19].

2.2.1. Equivalent Circuit with Real Values of res_k and p_k

Considering the RL series circuit of Fig.2, the admittance of the circuit can be easily calculated as [19]:

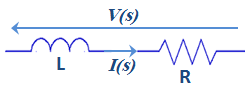Figure 2. Equivalent RL circuit for real poles synthesis

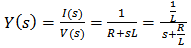(3)

The residue and pole of Y(s) are:

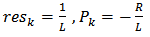(4)

So the R and L can be represented by res_k and p_k:

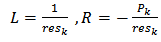(5)

2.2.2. Equivalent Circuit with Complex Pair Values of res_k and p_k

Assume that res₁, res₂, p₁ and p₂ are complex pairs, then excluding the constant term and the s–proportional term, F(s) may be expressed as [19]:

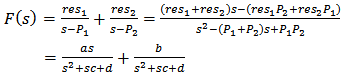(6)

Where

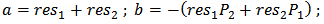
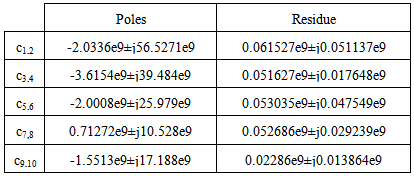
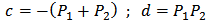Considering the RLC circuit shown in Fig.3, which is a combination of a simple series LR series and a CR parallel circuit, the admittance of the circuit, may be written in terms of its residues and poles as [19]:

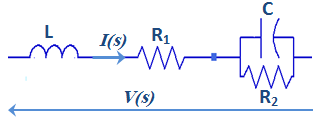Figure 3. Equivalent RLC circuit for complex pairs synthesis

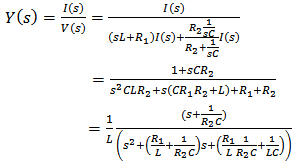(7)

Comparing equation (6) and (7), the following relations can be concluded [19]:

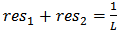(8)

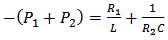(9)

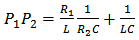(10)

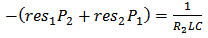(11)

The above equations can be solved and the RLC circuit parameters are [19]:

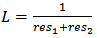(12)

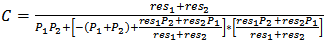(13)

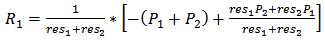(14)

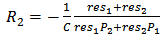(15)

The complete equivalent circuit can be established as shown in Fig 4, where C₀ represents the s–proportional term in F(s). R₀ is associated with the constant term in F(s). The RL series and the RLC combination circuit models can be selected according to the different two cases introduced above.

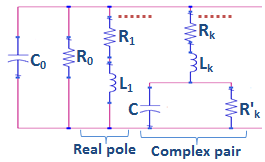Figure 4. SPICE-compatible equivalent circuit for antenna

3. Simulation Results and Discussion

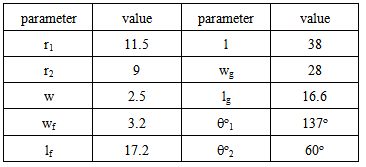
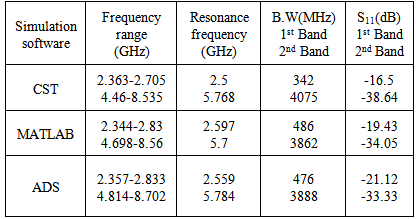
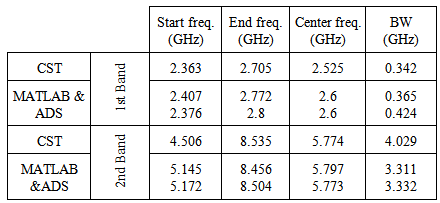
The dual-band crescent-shape monopole antenna proposed in [16] was chosen as a typical dual-band antenna in this investigation. The details of the antenna design are shown in Fig.5, and Table 1. The model was designed to match the 50 ohm feed line. The impedance at the feed line reference port was obtained using CST Microwave Studio. The theoretical results were obtained by considering an equivalent circuit of the antenna using MATLAB and ADS for calculating input impedance of the antenna. The results obtained from MATLAB and ADS softwares were then compared with the results obtained from the simulated antenna using CST. The derivations of the equivalent circuit are presented in the following three sections.

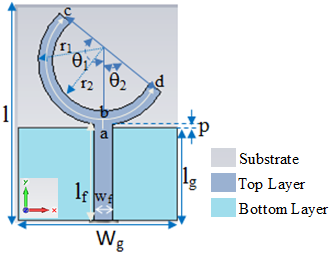Figure 5. Geometry of the dual band crescent-shape monopole antenna [16]

Table 1. Parameters of the designed antenna. All dimensions are in millimeters except )θ( in degree

3.1. Equivalent Circuit Derived from Reflection Coefficient Response

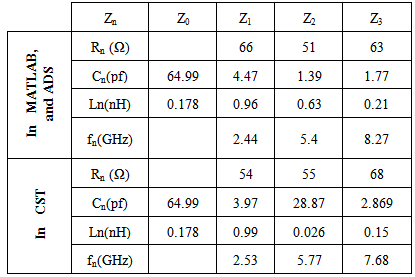
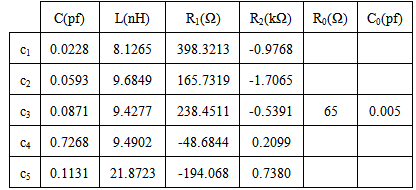
Figure (6a) shows the reflection coefficient curves of the considered antenna as obtained from CST simulations. Each of the three sharp dips in the curve can be considered to represent a resonance frequency. In Fig. (6b) the variation of the input impedance with frequency is shown, where the points marked by 1 to 6 represent real and imaginary values for the corresponding points indicated in Fig.6a. It can be seen from Fig.6b that the values of the real part at these points are around 50Ω while the values of imaginary parts are nearly crossing the zero. This means that the above resonating frequencies occur at matching points. According to the figure, three anti-resonance modes are observed in the investigated bands. The results of Fig. 6 lead to propose the equivalent circuit shown in Fig. (7). Table 2 shows the element values of the equivalent circuit model for the designed antenna. The values of resistors, capacitors and inductors are extracted from the CST simulation results, where these values are adjusted manually to obtain the proper response (response in MATLAB and ADS are similar to that in CST simulation). C₀ and L₀ represent the capacitance and inductance of the monopole antenna when the antenna operates at lower frequency and are properly chosen to resonate at the first resonance frequency of the antenna [20].

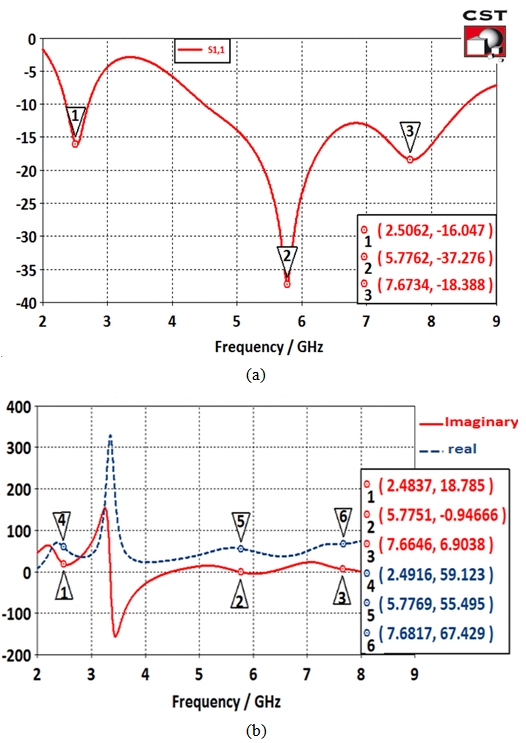Figure 6. Obtained results from CST software. (a)Reflection coefficient response, (b) the real and imaginary parts of (Zin) with frequency

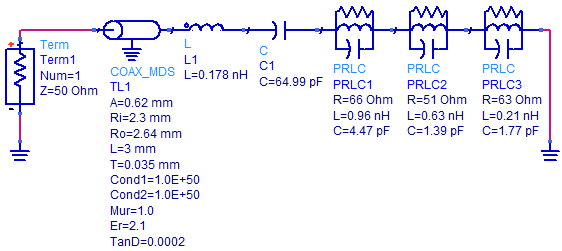Figure 7. Equivalent lumped-elements circuit model for antenna in ADS

Table 2. Element values of the equivalent circuit model for dual band crescent monopole antenna

Figure 8 compares the variation of the real part of (Z_in) with frequency as obtained from CST, ADS and MATLAB while Fig. 9 shows the variation of the imaginary part of (Z_in) with frequency. It can be seen from the figures that there is a good agreement between the results of CST, and those of ADS and MATLAB at the frequencies indicated in the figures (the points marked 1 to 3). However, some results at other frequencies are different. This is evident from CST simulation, at the frequency of 3.341GHz for both real and imaginary parts of Z_in. The results of ADS and MATLAB show much closer responses.

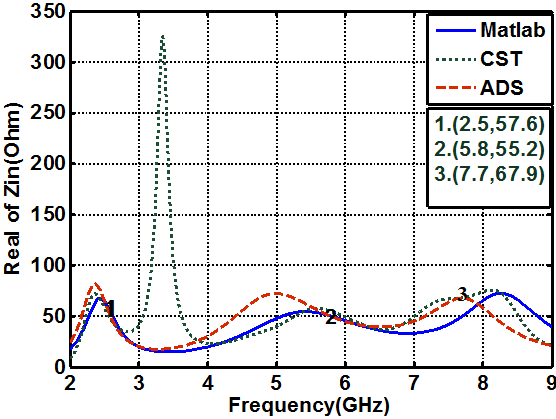Figure 8. Variation of real part of (Zin) with frequency

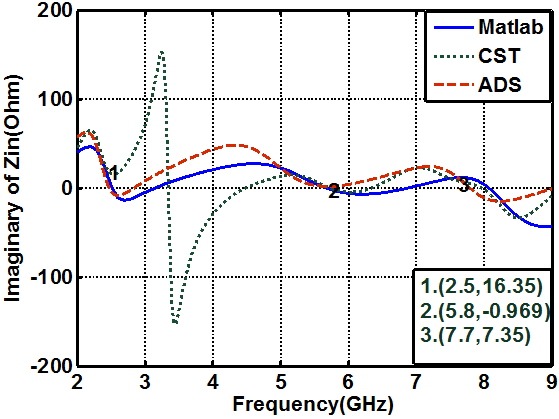Figure 9. Variation of imaginary part of (Zin) with frequency

Figure 10 shows the reflection coefficient response of the antenna obtained from CST simulation compared to the calculated response of the equivalent circuit model. Detailed parameters of the compared results of Fig. 10 are depicted in Table 3. These results are closer to each other in comparison with those obtained for the input impedance approach. The results show that the input impedance is well matched with VSWR< 2 bandwidth covering the two WLAN bands of (2.4GHz, 5.2GHz and 5.8GHz).

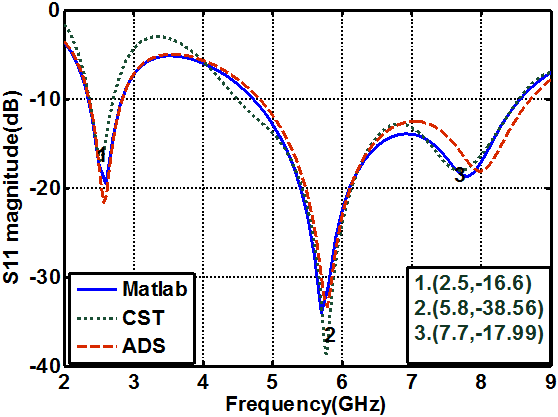Figure 10. Comparison of the reflection coefficient responses obtained from CST, ADS, and MATLAB

Table 3. Comparison of the frequency response characteristics of proposed antenna obtained from the three simulations software's; (CST, MATLAB and ADS)

3.2. Equivalent Circuit Derived from Input Impedance Response

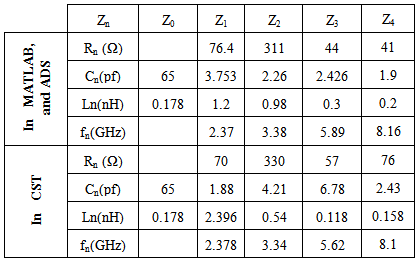
Around the resonance frequency, the antenna behaves like a series RLC circuit, where the derivative of the antenna's reactance with respect to frequency is positive. Near ranges of anti-resonance the general antenna behaves like a parallel RLC circuit and the frequency derivative of the antenna's reactance is negative [21]. When the antenna reactance moves from a negative (capacitive) value to a positive (inductive) value, in a finite frequency range, the frequency derivative of the antenna reactance is positive. If the impedance of the antenna changes from a positive (inductive) reactance to a negative (capacitive) reactance in a finite frequency range, the frequency derivative of the antenna's reactance is negative [21]. Therefore, by examination of the frequency derivative curves with respect to frequency of the antenna impedance the antenna can be modeled by either series or parallel RLC circuits.

Figure 11a, shows the input impedance responses of the antenna obtained from CST simulations. The input impedance is then represented by parallel RLC cells connected in series. At each mode, the imaginary part is nearly crossing the zero line and has a negative derivative while the real part has a local maximum. The proposed equivalent circuit model of the antenna is shown in Fig. 12. Figure 11b, shows the reflection coefficient response of the antenna. The points numbered from 1 to 4 represent the reflection coefficient for the corresponding points indicated in Fig.11a. As shown in the figures, the real part at point number 7 equals to 57.4Ω with S₁₁=-26.838 dB. The real part at point number 5 equals to 70Ω, and S₁₁=-10.7dB. The real part at point number 6 equals to 330Ω at S₁₁= -2.88dB. As can be seen from Fig.12, and Table (4), the input impedance is represented by four parallel RLC cells connected in series. The first cell represents the first band which resonates at 2.375GHz, the second cell represents the resonance frequency at 3.33GHz, the third and fourth cells (3,4), which are resonating at frequencies 5.62 and 8.1GHz respectively, represent the second band.

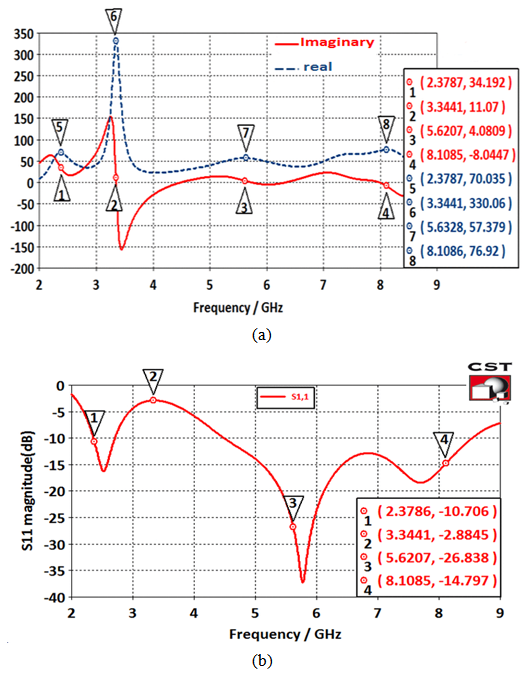Figure 11. (a) Variation of the real and imaginary parts of (Zin) with frequency. (b) Reflection coefficient response for the antenna

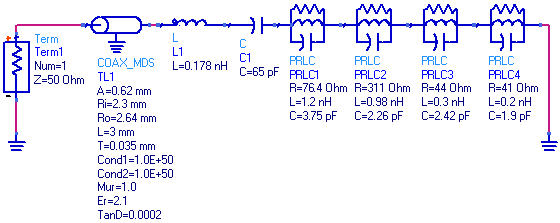Figure 12. Equivalent lumped circuit model for antenna in ADS

Table 4. Element values of the equivalent circuit model for the dual band crescent monopole antenna

Figures 13 and 14 show variations of real and imaginary parts respectively of the antenna with frequency, while Fig. 15 displays the reflection coefficient of the antenna as obtained from CST, compared to those obtained from the equivalent circuit using MATLAB, and ADS. The detailed characteristics of these responses are listed in Table 5. It can be noticed from Table 5 that the requirement for the 2.4 GHz WLAN band is adequately met. The second frequency band covers both the 5.2 and 5.8 GHz WLAN bands. However, wider band has been obtained here. The CST simulated results agree with those obtained from MATLAB and ADS with slight differences. The reason for this is that the structure simulator in the CST software accounts for all the coupling effects in the simulated antenna structure whereas in the equivalent circuit model only the individual lumped elements are taken into account with no account for the coupling between them.

Table 5. Comparison of the band characteristics obtained from the three modeling methods

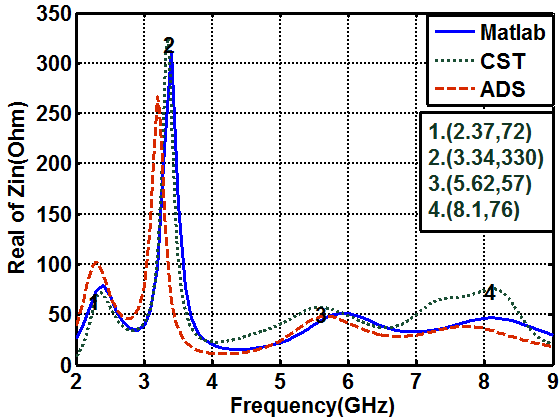Figure 13. Variation of real part of (Zin) with frequency

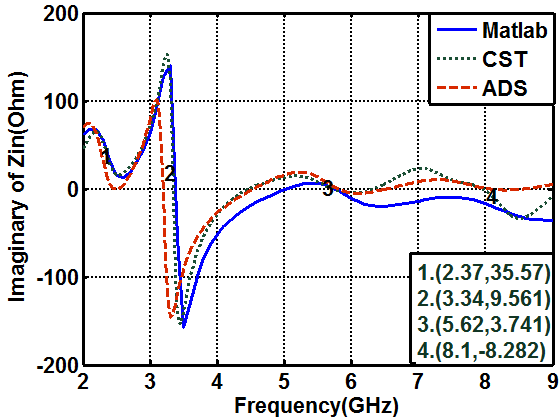Figure 14. Variation of imaginary part of (Zin) with frequency

3.3. Antenna Model Derived from SPICE-compatible Equivalent Circuit

The SPICE-compatible equivalent circuit modeling was applied to obtain equivalent circuit models of the input admittance. For example the dual-band monopole antenna, whose parameters are shown in Table 1, was considered.

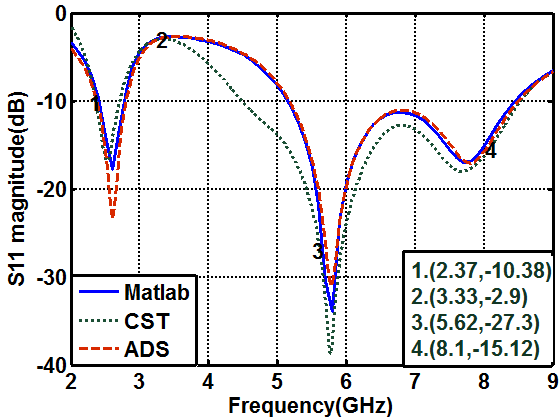Figure 15. Reflection coefficient responses versus frequency

The input admittance of the proposed antenna was estimated first from the simulation by the CST. Secondly, the simulated input admittance was fitted by means of the Vector Fitting (VF) technique. The initial poles in the VF procedure were chosen to be (10) linearly spaced poles, and the number of the used iterations was 3. The fitting procedure provided (5) complex pairs. The input admittance, and the root-mean-square error (rms-error) on the magnitude was found to be (<-29.87dB). The obtained extracted poles and residue are shown in Table 6. The synthesized component values of the equivalent circuit for the antenna are given in Table 7 where it is clear that few resistors have negative values, which cannot be realized practically. Thus the resulting rational approximation may still have few unphysical electrical components [22].

Table 6. Extracted poles and residue of antenna input impedance

Table 7. Synthesized component values for equivalent circuit of the antenna

Figures 16a, 16b, 16c, and 16d show plots of the real and imaginary parts of the admittance Y_in and impedance Z_in obtained from CST simulation, compared to those obtained from the VF fitting of the same input admittance, and those obtained by means of the SPICE equivalent circuit. As can be clearly seen, the proposed synthesis offers satisfactory approximations to the antenna input admittance and input impedance.

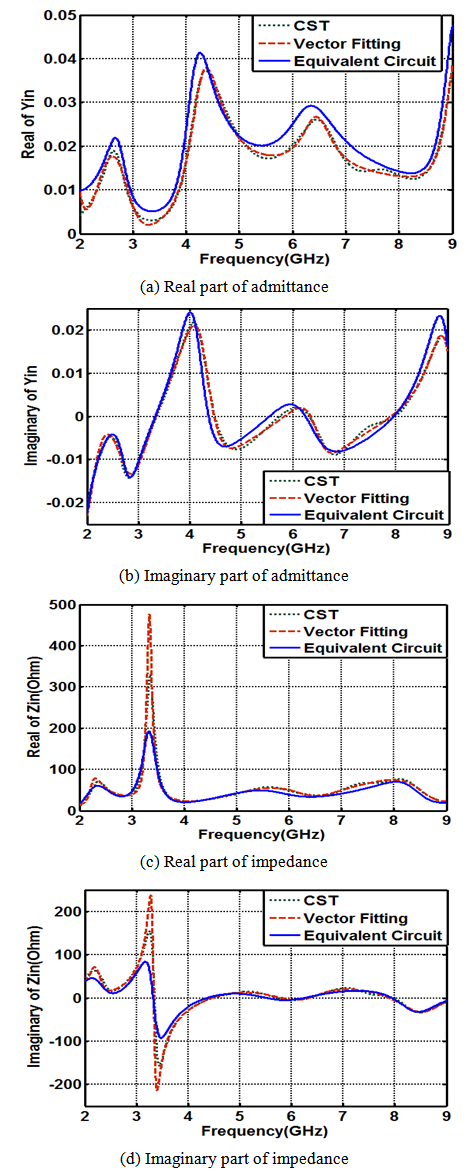Figure 16. Comparison of the admittance, and impedance parts of the antenna obtained from; CST simulation, the VF technique, and SPICE equivalent circuit

The reflection coefficient responses obtained from the CST software and equivalent circuit are shown in Fig. 17. The two responses cover the desired WLAN bands, and they show good agreement.

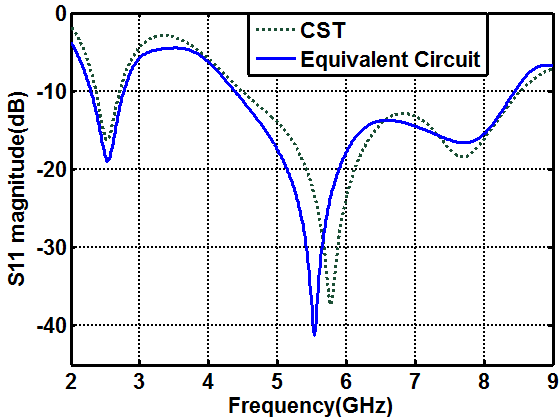Figure 17. Comparison of reflection coefficient of the antenna obtained by means of CST simulation and SPICE equivalent circuit

4. Conclusions

The modeling of a dual-band antenna has been demonstrated, a using crescent-shaped monopole antenna as a study case. An electrical model is applied to represent the input impedance of the antenna S two approaches. In the first approach, the input impedance is represented by parallel RLC-circuits connected in series. Each resonance is represented by a parallel RLC circuit derived either from the reflection coefficient response or the input impedance. The obtained results showed that the equivalent circuit extracted from the real and imaginary parts of input impedance gives good details about the whole studied band (from 2 to 9GHz). However, the equivalent circuit extracted from the reflection coefficient response gives good details about the design bands only (2.4, 5.2, and 5.8GHz). The second investigated approach is SPICE–compatible equivalent circuit using vector fitting technique. The formulation of the transfer function in rational polynomial can identify the poles and zeros of the antenna system. Each RLC circuit is proposed as an equivalent representation for a complex pole pair. The model responses using MATLAB and ADS showed good agreement with those obtained from the CST simulation. While most of the modeling methods have considered either narrow or UWB antenna, it has been demonstrated that the methods are equally applicable to dual band antennas.

ACKNOWLEDGEMENTS

The authors wish to acknowledge valuable discussions with Prof RaedA.Abd-Alhameed / Bradford university, UK during the preparation of the manuscript.